不同简化算法模型模拟都江堰灌区参考作物蒸散量

娄忠秋, 李 桢

(1.四川水利职业技术学院, 四川 都江堰 611800;2.四川大学 水力学与山区河流开发保护国家重点实验室/水利水电学院, 成都 610065)

蒸散(Evapotranspiration,ET)作为唯一一项同时出现在水平衡和能量平衡方程的因素，在农业水管理及水文预报中扮演着重要的角色[1]。目前对ET的监测主要有实测法和估算法两种，估算法由于其成本低、精度高、便于实现，已被广泛应用于ET估算当中[2-3]。参考作物蒸散量(Reference crop evapotranspiration,ET0)是基于作物系数法计算ET的重要参数之一，其准确估测对农田蒸散预测及农田水分管理意义重大。目前对ET0的计算多采用公式法进行，该方法在仅需气象资料的条件下，即可完成对ET0的预测，原理简单，数据获取渠道较广泛，在无法获得ET0实测资料的条件下，找出适合该地区的ET0计算公式是国内外研究的热点。国际粮农组织FAO-56分册因Penman-Monteith(PM)模型，综合考虑了空气动力学项和辐射项，物理意义明确，推荐该模型为计算ET0的标准模型[4-5]。但该方法对气象资料的要求较高，需要长时间序列的温度、风速、相对湿度和辐射等资料，在资料缺乏及条件落后的地区难以实现，因此对ET0简化计算模型的研究已成为了热点[6]。

由于不同ET0计算模型在不同区域的计算精度不同，国内针对不同气候条件下的最优ET0计算模型选取做了一定的研究，也为本文研究提供了一定的理论基础。已有研究表明，辐射是影响ET0最关键的因素之一[7-8]，约80%是由于温度与辐射引起的，因此，本文选择Priestley-Taylor(PT)模型等辐射法模型，并计算不同机器学习模型在考虑辐射前后的精度，通过比较不同模型的精度，进一步验证了辐射对ET0计算模型精度的影响。李晨等[9]分析了适用于四川省不同地区的ET0简化计算模型，指出了由于四川省温度日差大，使得基于辐射的PT模型在四川省的计算精度普遍较高。同时，机器学习模型由于其计算原理简单、计算精度较高，现已普遍应用于ET0精确估算当中，Feng等[10]研究了3种机器学习模型在川中丘陵区的适用性，指出极限学习机模型(ELM)及广义回归神经网络模型(GRNN)模型的计算精度明显高与普通ET0简化计算模型，同时考虑辐射后模型精度提高。张薇等[11]在河北省同样指出机器学习模型的计算精度高于HS模型，验证了机器学习模型的科学性。本文的研究在找出适用于都江堰灌区最优计算模型的同时，进一步说明了辐射对模型计算的重要性。

都江堰灌区面积达2.32万km2，总耕地面积超过1.10万km2，是国内重要的大型灌区之一[12]，研究都江堰灌区最优ET0简化算法，对当地灌溉决策及粮食生产有着重要的意义。已有研究表明，辐射是影响都江堰灌区的ET0最关键因素[8]，本文选择辐射法计算ET0中的Priestley-Taylor(PT)模型、Makkink(MK)模型、Ritchie(RC)模型和机器学习算法中的极限学习机(ELM)模型、广义神经网络(GRNN)模型，基于1961—2017年的逐日气象资料，选出适用于都江堰灌区的ET0简化计算模型，该模型的提出可为当地水资源决策的制定提供理论依据。

1 研究方法

1.1 研究区概况及数据来源

都江堰灌区(103°15′—105°50′E，29°31′—31°25′N)地处四川平原，属亚热带季风气候。灌区空气湿润，多年平均相对湿度可达88%，年降雨量约1 200 mm，温度适中，年平均气温15.10～17.40℃，年平均日照时数超过1 000 h。都江堰灌区的正常运行，直接影响着整个四川省的灌溉、防洪、运输和发电，对当地生活起着至关重要的作用。本文选择灌区附近的成都、都江堰、乐山、遂宁和雅安5个站点1961—2017年的逐日气象资料，计算不同模型的ET0数值，找出最优模型。

本文数据均来自于国家气象中心，数据控制良好，气象资料主要包括站点日最高气温(Tmax)、最低气温(Tmin)、日照时数(n)、相对湿度(RH)和10 m处风速(U10)。

1.2 研究方法

1.2.1 Penman-Monteith模型(PM) 1998年FAO-56分册推荐的Penman-Monteith(PM)模型为ET0计算的标准模型，其模型型式及参数意义见文献[13]。

1.2.2 Priestley-Taylor模型(PT) PT模型公式如下[14]：

(1)

式中：ET0-PT为由PT模型计算得到的ET0(mm/d)；α为常数，取1.26；λ为水汽化潜热(MJ/kg)；γ是干湿计常数(kPa/℃)；Δ是蒸汽压曲线的斜率(kPa/℃)；Rn是作物表面的净辐射[MJ/(m2·d)]；G是土壤热量通量密度[MJ/(m2·d)]。

1.2.3 Makkink模型(MK) MK模型公式如下[15]：

(2)

式中：ET0-MK为由MK模型计算得到的ET0(mm/d)；Rs为太阳辐射[MJ/(m2·d)]；其余参数意义与前文一致。

1.2.4 Ritchie模型(RC) RC模型公式如下[16]：

ET0-RC=α1×[0.00387Rs×(0.6Tmax0.4Tmin+29)]

(3)

式中：ET0-RC为由RC模型计算得到的ET0(mm/d)；Tmax为最高温度(℃)；Tmin为最低温度(℃)；α1为经验系数，取值如下：

(4)

1.2.5 极限学习机模型(ELM) 极限学习机模型(ELM)是一种简单的单隐层前馈神经网络学习算法[17]。图1为ELM模型原理图，采用Matlab2016年软件对ELM模型进行编程计算，输入参数为Tmax，Tmin和Rs，以1961—2000年的数据训练模型，以2001—2017年的数据验证模型精度。

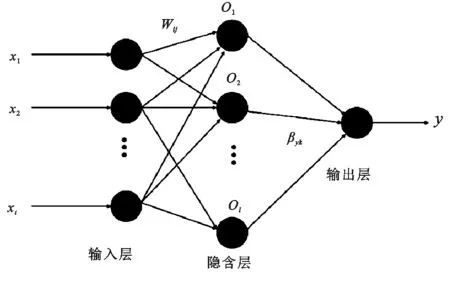
图1 ELM模型计算原理

1.2.6 广义神经网络模型(GRNN) 本文采用的GRNN由输入层、模式层、求和层和输出层等4层神经元组成，利用GRNN输入参数为Tmax，Tmin和Rs，以1961—2000年的数据训练模型，以2001—2017年的数据验证模型精度，在Matlab 2016年中直接调用GRNN函数，调用格式及模型参数见参考文献[18]。

1.2.7 评价指标体系 本文模型模拟结果评价指标体系采用相对均方根误差(RMSE)、相对误差(RE)、模型效率系数(Ens)和决定系数(R2)综合分析精度，具体公式如下。

(5)

(6)

(7)

(8)

2 结果与分析

2.1 各模型ET0日值计算结果及精度比较

图2为都江堰灌区各站点不同模型模拟ET0日值与PM模型模拟值的比较。可以看出，GRNN模型和ELM模型在不同站点的精度普遍较高，其中GRNN模型的R2，RMSE，Ens分别为0.835 7～0.886 3，0.366～0.497 mm/d和0.832～0.879，ELM模型的R2，RMSE，Ens分别为0.852 4～0.911 0，0.363～0.413 mm/d和0.856～0.903，同时ELM模型拟合方程斜率为0.960 5～1.036 7，表明该模型的计算结果与PM模型误差最低，且一致性最高，同时可最好地反映出气象因子与ET0之间的关系。与机器学习模型相比，PT模型在都江堰灌区的模拟精度较高，而其余ET0简化计算模型的模拟精度较低，其中MK模型在不同站点的拟合方程斜率为0.789 3～0.876 1，RC模型为1.169 8～1.329 3，与标准值“1”偏差较大，同时2个模型的RMSE分别达到了0.498～0.574 mm/d和0.557～0.617 mm/d，R2和Ens均明显低于其余模型，由此可知，ELM模型、GRNN模型和PT模型的计算精度明显高于MK模型和RC模型。

2.2 各模型ET0月值计算结果比较

图3为都江堰灌区不同站点不同模型模拟ET0月值结果比较及相对误差(RE)年内变化。图3显示，不同模型模拟的ET0月值在年内的变化趋势基本一致，呈开口向下的二次抛物线型式，其中不同模型模拟的ET0月值主要集中在3—10月的主要作物生长季，占全年ET0的82.9%～87.1%，其值在7月最大，而在12月、1月最小；综合比较不同模型与PM模型的计算结果，可以看出MK模型在不同站点均低估了ET0，而RC模型则均高估了ET0值，5种模型中精度较高的为ELM模型、GRNN模型和PT模型。

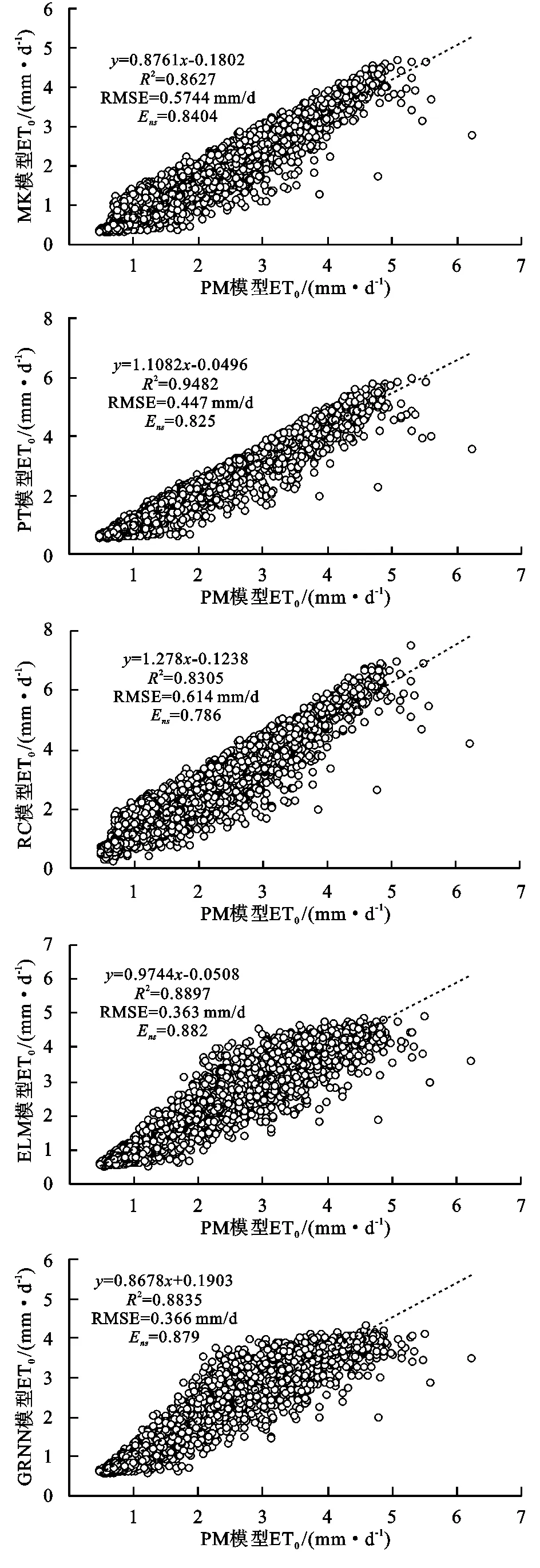
图2 都江堰灌区成都站各模型ET0日值计算结果比较

由相对误差年内变化图可以看出，与PM模型相比，MK模型与RC模型的计算精度较差，其中MK模型RE均为负，表明计算结果偏低，同时其计算精度在全年内呈现先提高后降低的趋势，在1月和12月的计算精度最低，相对误差最高可达到-32.15%，RC模型RE均为正，表明计算结果偏高，其相对误差在年内呈先减小后增加的趋势，在1月和12月的计算精度最低，相对误差最高可达到35.75%；PT模型、ELM模型和GRNN模型计算精度普遍高于RC模型和MK模型，3种模型RE变化范围分别为-4.36%～18.74%，-2.37%～14.38%和-10.49%～17.58%，ELM模型和GRNN模型RE在温度较高时误差较小，在秋、冬温度较低时的误差相对较大，说明在温度较低时机器学习模型模拟精度相对较低，这与冯禹等[5]人的研究结论基本一致。综上所述，PT模型、ELM模型和GRNN模型的计算精度较高，而ELM模型计算精度最高，可作为都江堰灌区ET0简化计算模型使用。

2.3 辐射对模型模拟精度的影响

由于辐射是影响都江堰灌区ET0形成的主要原因，为找出辐射法计算都江堰灌区ET0的优势，更形象解释辐射的重要性，本文计算了在输入变量Tmax，Tmin和Rs和仅输入变量Tmax，Tmin时的ELM模型、GRNN模型计算精度，结果见表1。表1显示，在输入辐射项Rs后，ELM模型与GRNN模型的计算精度明显提高，输入Rs前后，在不同站点ELM模型R2提高了0.03～0.05，RMSE降低了0.06～0.16 mm/d，Ens提高了0.03～0.11，GRNN模型R2提高了0.03～0.05，RMSE降低了0.05～0.07 mm/d，Ens提高了0.03～0.07，表明输入Rs可明显降低误差同时提高计算结果一致性，同时ELM模型在输入Rs后计算精度提高更显著。

3 讨 论

本文研究表明，在ET0简化计算模型中，PT模型计算精度较高，RC模型和MK模型计算精度较低。不同模型计算精度主要与当地区域下垫面情况、气候及所在海拔等因素有关[19]。都江堰灌区位于四川平原地区，地处亚热带季风气候，气候湿润，表明PT模型在湿润地区的计算精度较高，这与李晨[9]、符娜[20]等的结果一致；MK模型误差普遍在0.55 mm/d以上，精度较低，这可能是由于模型式中的参数为常数，无法根据不同区域特点选择最适宜的值，同时MK模型的计算数值主要与当地饱和蒸汽压有关[21]，导致其在湿润地区的计算精度普遍较低，更适用于干燥区域，这与左德鹏等[22]的结论一致；RC模型不但与辐射值有关，其准确值也与当地温度变化有关，都江堰灌区常年平均温度基本在16.0℃左右，温度日较差小，导致与温度有关的方法计算精度均较低，这可能也是RC模型在都江堰灌区计算误差较大的原因之一。

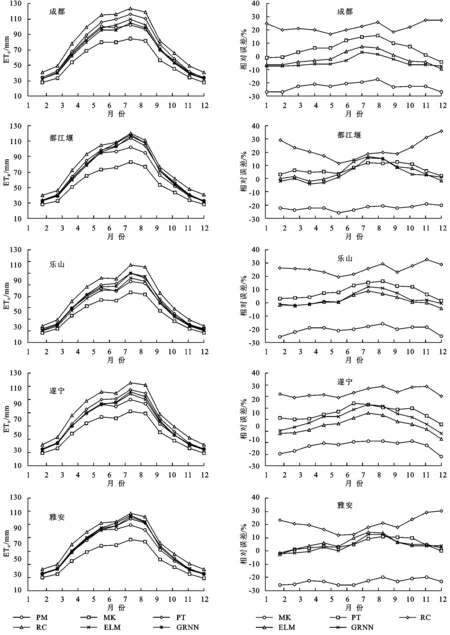
图3 都江堰灌区不同站点各模型ET0月值计算结果比较及相对误差年内变化

表1 考虑辐射对模型精度影响

本文指出WNN模型的计算精度较低，该模型原理主要基于梯度下降算法，导致其收敛速度较慢，同时模型学习结果存在较大的不确定性，使得该模型计算精度偏低[23]，而GRNN模型和ELM模型的计算精度普遍较高，这可能是由于模型综合考虑了ET0与气象因子之间的线性关系，可以较好反映出ET0变化规律，从而对ET0进行预测，ELM模型由于其输入权值和隐含层偏差被随机初始化给定，导致了输出权值利用广义逆进行计算，使得模型较传统的机器学习模型具有学习速度快等优点，保证了其计算精度[24]。而GRNN模型依据概率最大原则，无需设置具体模型参数，学习样本一经确定，则相应的网络结构和各神经元之间的连接权值也随之确定，导致其较传统神经网络模型精度有所提高，但GRNN模型中的参数虽研究区域不同，所取值也不尽相同，导致其存在自适应能力弱等缺点[25]，这也是GRNN模型计算精度低于ELM模型的主要原因之一。由于GRNN模型与ELM模型均属于机器学习模型，其适用区域不存在一定的限制，可在不同气候特点区域内均取得较高的精度，但在模拟时需有一定的数据进行训练，因此，在应用过程中，应保证具有足够长的基础数据序列来训练模型，以保证模型的计算精度。

本文以PM模型计算结果为基础，验证了不同模型的计算精度，虽PM模型为推荐的标准模型，但在实际应用过程中应以实测数据为基准，同时验证PM模型的适用性，并对其参数进行优化。同时本文计算机器学习模型时输入的Rs的值是由气象站点日照时数推算而得，在今后的应用中也应采用实测的辐射Rs的值进一步基于ELM模型和GRNN模型推求ET0的值。

4 结 论

(1) 在模拟ET0日值时，RC模型和MK模型与PM模型结果的拟合性较差，而ELM模型、GRNN模型和PT模型的计算精度的拟合方程斜率更接近于标准值“1”，同时RMSE较低、而R2和Ens较高；

(2) 不同模型模拟ET0月值在年内变化的趋势基本一致，而RC模型结果高估了ET0，MK模型低估了ET0，GRNN模型和ELM模型在模拟ET0月值时的计算精度较高；

(3) 辐射是计算都江堰灌区ET0需关键考虑的因素，考虑辐射之后，GRNN模型和ELM模型的计算精度明显提高，同时ELM模型在计算ET0日值和月值时的计算精度均较高，可作为都江堰灌区在气象资料缺失情况下的ET0标准计算模型。