基于RSI的GPS坐标时间序列瞬态地壳形变信号探测

成国辉，罗 勇，刘 斌，匡翠林

(1. 长沙市规划勘测设计研究院，湖南 长沙 410007； 2. 长沙理工大学交通运输工程学院测绘工程系，湖南 长沙 410114； 3. 中南大学地球科学与信息物理学院，湖南 长沙 410083)

瞬态形变是由地壳构造运动(如震后地壳松弛形变、板块边界走滑断层、消减带慢地震等)导致的位移变化[1]。GPS观测精度突破毫米级使得对坐标序列中的瞬态形变信息进行探测成为可能。GPS坐标时间序列中瞬态形变探测在早期主要是基于物理模型来反演坐标序列中的瞬态变形信号[2- 4]，该类方法实现起来稍复杂，且适用于监测网较小的情况，在断层几何模型或格林函数相关的先验信息不准确的情况下，给形变信息的提取带来较大的偏差。南加州地震中心(southern California earthquake center,SCEC)于2010年提出基于SCIGN(sdouthern California integrated GPS network)监测网开展瞬态形变信息探测的研究[5]，各学者陆续提出并发展了一些探测瞬态形变信息的算法：网络反演滤波[6](network inversion filter，NIF)、网络应变滤波[7](network strain filter，NSF)、Kalman- PCA方法[8]、协方差描述分析[9](covariance descriptor analysis，CDA)、高斯小波变换[10]、Bayesian模型[11]等。此外，在地质构造运动活跃地区，探测GPS观测序列中的瞬态形变信号也一直是研究的热点问题[12- 14]。

相对强弱指数(relative strength index，RSI)是1978年首次由Wilder提出来的，最初广泛用于期货交易中[15]。RSI对序列中异常信息特别敏感，因此适用于对事件的检测。本文提出利用RSI对GPS测站序列中瞬态形变进行探测的方法，并利用该方法对卡斯卡迪亚古陆选取的10个GPS测站坐标时间序列进行分析，探测发生瞬态形变测站的时间尺度、滑移大小；最后利用探测到的瞬态形变进行建模，减小残差序列的方差，完善坐标时间序列。

1 RSI基本原理

RSI方法在股票市场中被证明是一种很有价值的技术指标，其计算公式为[15]

(1)

(2)

式中，Uj和Dj分别为在指定时间段n内的涨幅与跌幅。采用简易移动平均法，得到涨幅与跌幅的比率RS，通过式(2)得到该时间的RSI，其范围为0～100。通过RSI值可以判断各个时间段内的整体趋势是上升还是下降。如股市RSI分析中普遍选取RSI值上下限的规则为：当n=14时，范围为(30,70)；当n=20时，范围为(40,60)。

然而，GPS数据不同于股市数据，GPS时间序列包含时空噪声，对RSI分析产生了不确定性，因此在分析前需对原始序列进行滤波，去除部分共模误差和高频噪声；且RSI值选取范围也变大，为(20,80)。对于滤波后的时间序列，采取n=21 d的简易滑动平均法计算各个时间段的RSI，并定义RSI值大于50的所有RSI的平均值为上限阈值，小于50的所有RSI的平均值为下限阈值。在计算出所有测站各个方向的RSI值和阈值后，计算各测站RSI超出阈值数，剔除在最大阈值与最小阈值之间的RSI值。本文选取连续数超过7 d的RSI值，将其作为可能发生瞬态形变的时间段，因为大部分慢滑移事件时间跨度是超过7 d的。

2 基于RSI的瞬态形变探测与GPS坐标时间序列改正

2.1 RSI瞬态形变探测实例

数据来源于美国SOPAC(Scripps orbit and permanent array center)数据处理中心,使用GAMIT软件解算并与QOCA(quasi- observation combination analysis)软件包结合处理,选取ITRF2008框架下的60个GPS测站。测站GPS时间序列经过PCA滤波去除了部分高阶误差，减小了不确定性；通过最小二乘取出时间序列的线性项、季节信号、同震和震后位移，去除时间序列中的线性项，并采用三倍中误差法来探测和剔除粗差；对剔除粗差后的时间序列进行插值补齐，对于小于3 d的数据缺失采用三次样条插值，对于缺失较长的数据，选择直接跳过该段缺失的数据，从下一段连续的时间序列继续进行RSI分析。

本文选取10个发生瞬态形变的测站进行分析，分别为albh、bamf、coup、nano、p397、p403、p405、p425、sc02、sc03测站。采用RSI方法对E方向时间序列的瞬态形变进行研究分析，测站时间序列如图1所示。通过目测可以看出，瞬态形变是往W方向偏移的，且10个测站的时间序列各自在不同的时段发生了瞬态形变，在某个固定时段，部分测站同时发生瞬态形变。

图2是E方向10个测站的RSI值，从图中可以看出，10个测站的RSI值整体比较稳定，保持在50左右，说明测站序列整体是比较平稳的。然而，每个测站部分时间段的RSI值并不平稳，如图中椭圆标记处，这些不平稳的时间段可能就是发生瞬态形变的位置。通过计算，北方向(N)、西方向(E)和垂直方向(U)3个方向RSI平均阈值分别为52.8/47.1、53.4/46.4和52.9/47.1，由于E方向偏移最大，RSI的平均阈值也最大，因此利用E方向时间序列进行瞬态形变探测也更具代表性。由于E方向各测站的瞬态信号整体往W方向(整体趋势下降且RSI值都小于50)偏移，且大部分是同一时段发生，而对于探测出的极小部分往E方向(整体趋势上升且RSI值都大于50)偏移的瞬态信号，并没有作详细分析。因此，本文仅对E方向的测站序列往W方向发生的瞬态形变进行探测研究。

为了获得发生瞬态形变的开始时间、结束时间、持续时间和位移，对图1中的每个时间序列进行RSI定量分析，采用简单移动平均法，计算连续21 d的RSI，筛选出至少连续7 d RSI值小于下限阈值(46.4)的时间段，认为该时间段内发生了瞬态形变。图3为10个测站RSI超出阈值数的统计结果，图中RSI超出值越大，说明在此时间段内发生瞬态形变的偏移量越大，RSI越密集，说明发生瞬态形变的时间段更长或在此时间段内发生瞬态形变的测站越多。此外，从图中还可以看出，瞬态形变的出现具有一定的规律性，呈似年周期变化。

对比图1与图3，在图1画线处的瞬态形变基本都可以探测出，表1是对这10个测站发生瞬态形变的记录的统计分析。从表中也可以看出，瞬态形变存在12～18个月的周期性，持续天数长短不同，最大偏移量不等(最大偏移量是该时段内最大最小位移值之差)，同时段发生瞬态形变的测站数不同。同时段发生瞬态形变的测站数不同，分别为：事件1，albh、bamf和sc02；事件2，albh、bamf、nano和sc02；事件3，albh、bamf、coup、sc02和sc03；事件4，albh、bamf、coup、sc02和sc03；事件5，albh、bamf、coup、p403、sc02和sc03；事件6，albh、bamf、coup、p403、sc02和sc03；事件7，p397和p425；事件8，albh、bamf、coup、p403、p405、p425、sc02和sc03；事件9，albh、coup、p397、p403、p405、p425、sc02和sc03；事件10，albh、bamf、nano、p403、sc02和sc03；事件11，albh、bamf、nano、p403、sc02和sc03；事件12，p397、p405、p425、sc02和sc03。albh、bamf、sc02和sc03瞬态形变的周期性最明显，且sc03整体的瞬态偏移更大，说明sc03站受慢滑移事件影响是比较大的。

2.2 时间序列中瞬态形变改正

为了利用探测得到瞬态形变信息改善GPS坐标时间序列，使用RSI探测到的瞬态形变信息对每个时间序列利用偏移改正和不用偏移改正分别进行建模，参考模型如下[16]

y(ti)=a+bti+csin(2πti)+dcos(2πti)+

(3)

式中，a为初始位置；b为速率；c、d、e和f分别为年、半年周期项系数；g为偏移系数；v为误差；t为时间；H为阶梯(heaviside step)函数，用来描述瞬态形变的发生。上文通过RSI探测到瞬态形变发生的时间及形变量，结合探测信息进行建模。图4为利用RSI方法探测的瞬态形变建模后的残差时间序列，可以看出改正后的时间序列一定程度上减小了阶跃的影响。使用方差减少率来评定时间序列的改进，公式如下

(4)

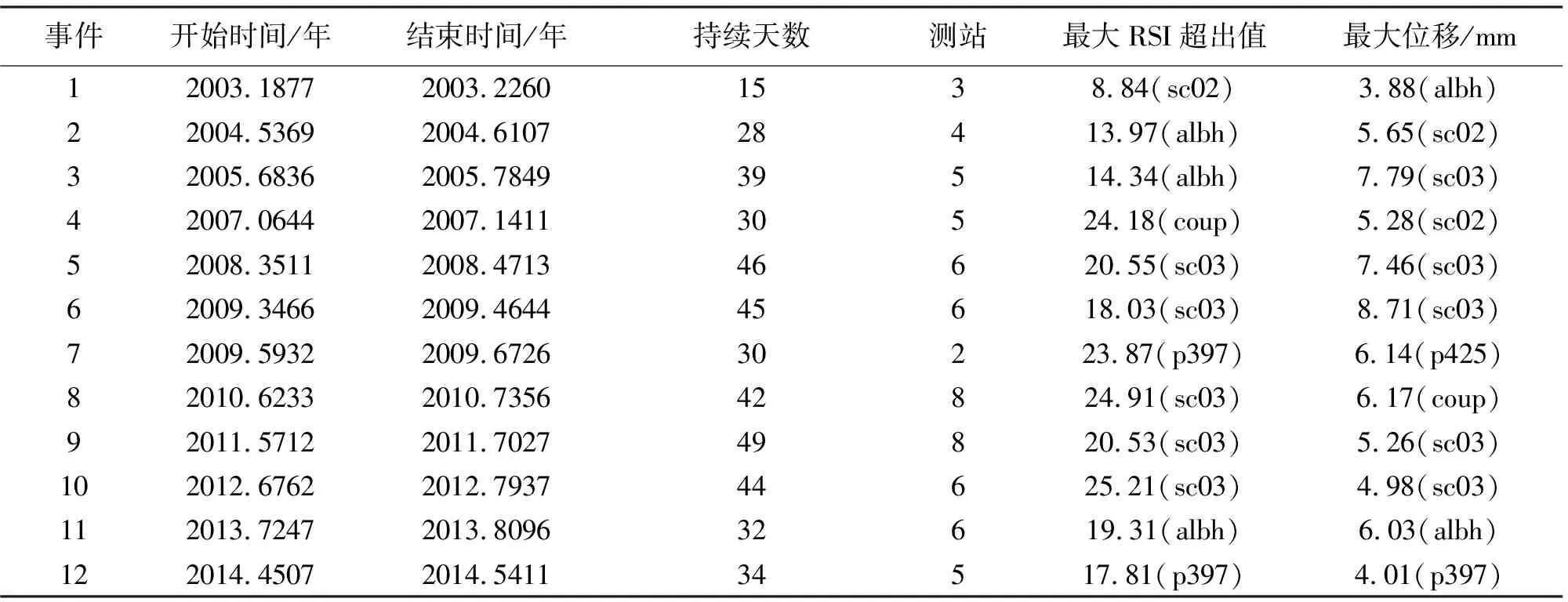
表1 试验中10个GPS测站的慢滑移事件记录

表2 各测站E、N、U方向的残差时间序列偏移改正后的方差减少比例(%)

从以上分析可以得出，RSI方法是一种有效的探测方法，它通过对一个区域各个测站序列进行RSI分析，讨论可能发生形变的时刻，并通过探测到的形变时刻，使用模型进行改进，去除其中的瞬态形变信号，从而为序列的速率评估和噪声估计提供便利。

3 结 语

瞬态形变在地球物理中有着重要作用，若其没有被正确探测与修正，将影响GPS坐标时序的噪声特性及其测站的速率估计，从而会直接影响GPS坐标序列的应用水平。本文将RSI方法应用到GPS时间序列地壳瞬态形变信号探测中，实例应用表明，RSI是一种有效的探测手段，且能给出瞬态形变发生的时间起点、持续时间及形变大小等详细信息。利用探测到的瞬态形变信息对时间序列进行建模改正，结果表明，使用偏移改正后的残差时间序列方差有明显减小，有利于进一步准确分析GPS坐标时间序列噪声特性和进行测站坐标速率估计。