基于电网的采样感知加权循环调度算法
谭鑫 李晓卉 刘振兴 丁月民 赵敏 王琦

摘 要:针对智能电网相量测量设备竞争使用有限的网络通信资源时,会因资源分配不均而导致数据包延时或丢失,进而影响电力系统状态估计的精度这一问题,提出了一种采样感知加权循环(SAWRR)调度算法。首先根据电网相量测量单元(PMU)采样频率和数据包大小的特性,提出了基于PMU业务流均方差的权重定义方法;然后设计了相应的PMU采样感知迭代循环调度算法;最后将该算法运用到PMU采样传输模型中。该算法能自适应地感知PMU的采样变化,及时调整数据包的传输。仿真结果表明,与原始的加权循环调度算法相比,SAWRR算法减少了95%的PMU采样数据包的调度时延,降低了一半的丢包率,增加了两倍的吞吐量。将SAWRR算法运用到PMU数据传输中有利于保证智能电网的稳定性。
关键词:智能电网;相量测量;调度算法;权重;采样
Abstract: When the smart grid phasor measurement equipment competes for limited network communication resources, the data packets will be delayed or lost due to uneven resource allocation, which will affect the accuracy of power system state estimation. To solve this problem, a Sampling Awareness Weighted Round Robin (SAWRR) scheduling algorithm was proposed. Firstly, according to the characteristics of Phasor Measurement Unit (PMU) sampling frequency and packet size, a weight definition method based on mean square deviation of PMU traffic flow was proposed. Secondly, the corresponding iterative loop scheduling algorithm was designed for PMU sampling awareness. Finally, the algorithm was applied to the PMU sampling transmission model. The proposed algorithm was able to adaptively sense the sampling changes of PMU and adjust the transmission of data packets in time. The simulation results show that compared with original weighted round robin scheduling algorithm, SAWRR algorithm reduces the scheduling delay of PMU sampling data packet by 95%, halves the packet loss rate and increases the throughput by two times. Applying SAWRR algorithm to PMU data transmission is beneficial to ensure the stability of smart grid.
Key words: smart grid; phasor measurement; scheduling algorithm; weight; sampling
0 引言
隨着智能电网(Smart Grid)快速发展,如何保证其运行的稳定性和高效性是近年来研究重点。电网广域监测系统(Wide Area Measurement System, WAMS),通过在电网关键测点布局基于全球定位系统(Global Positioning System, GPS)的同步相量测量单元(Phasor Measurement Unit, PMU),实现对电网运行主要监测数据的实时高速率采集,并通过通信网络实时传送到广域监测主站系统,从而提供对智能电网正常运行与事故扰动情况下的实时监测与分析计算,及时获得并掌握电网运行的动态过程,为智能电网提供监测、保护和控制之用,因此PMU与主站系统之间数据传输的高效性、完整性和及时性,是实现智能电网系统稳定性的重要保证[1-2]。
由于WAMS中有大量的PMU同步采样实测数据[3]需要传送,为了保证电网监测的完备性和数据的高效性,近几年来,不少学者在PMU的布局和数据预处理上进行研究,并取得了显著效果。文献[4]中提出了最优PMU通信链路布局(Optimal PMU-communication Link Placement, OPLP),与传统的最优PMU布局模型相比,OPLP可以显著降低总安装成本;文献[5]中提出一种线性迭代算法搜索满足给定的同步相量可用性分布的最小数量的PMU的放置;文献[6]中利用PMU数据中的固有相关性,利用空间和时间冗余,提出了一种两阶段压缩算法,减少物理存储器需求;文献[7]中提出一种实时数据压缩和适用于WAMS的IEEE C37.118协议技术,该压缩改进协议技术可以在动态和稳定状态下高精度地将数据包大小减小大约75%;然而,随着智能电网的不断普及发展,电网PMU的数量不断增加,在网络带宽有限的条件下,主站系统通过WAMS接收PMU数据时,如何设计一种公平的调度算法,以实现对不同采样频率的PMU的数据流提供实时的调度越来越引起人们的关注[8-9]。
针对这个问题,本文将PMU采样特性和调度算法相结合提出了一种基于采样感知的加权循环(Sampling Awareness Weighted Round Robin, SAWRR)算法。該算法是根据每个PMU采样频率、包的大小和加权循环(Weighted Round Robin,WRR)权重来确定每个PMU的权重。通过对SAWRR算法和WRR算法进行仿真分析,结果表明SAWRR算法在平均时延、丢包率和吞吐量等性能上都要优于WRR算法。
1 WAMS结构及调度算法
1.1 WAMS结构
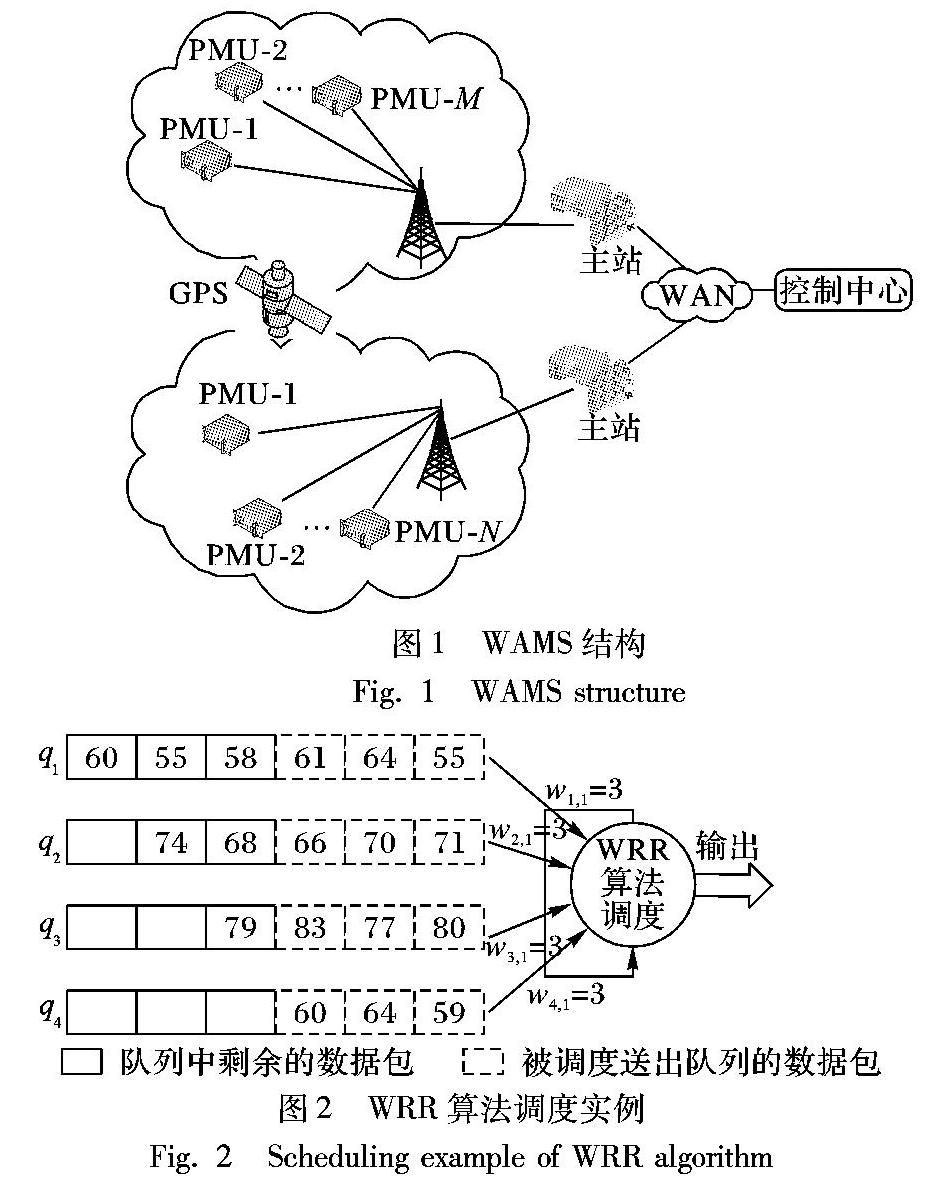
WAMS结构如图1所示,其基本组件是PMU和主站系统以及联系两者的广域网(Wide Area Network, WAN)[10-11]。PMU是一个通过GPS信号同步采样电流电压测量数据并提供相位、幅值和频率信息的设备[12]。主站收集来自不同PMU的测量值,对其进行时间校准后,送往控制中心用于电力系统的状态估计、动态监测和暂态稳定性分析。
由图1可知,多个PMU将收集到的数据通过WAN传输给主站,主站间存在交换PMU数据的需求。未来随着智能电网的不断发展,WAMS中PMU的数量也会随之增长。如果为新增的PMU不断增加新的网络通信资源是不现实的。不同采样频率的PMU竞争使用有限的网络通信资源进行传输时,可能因为资源分配不均而导致部分PMU因缺乏网络传输资源而引发时延的增加和大量丢包。PMU测量值的缺失,会导致主站对电力系统状态估计的精度降低,不利于对电网进行相关的保护、检测和控制,进而影响电网的稳定性。
为了解决上述WAMS中为PMU均衡分配网络通信资源的问题,需要在主站系统中引入调度算法合理均衡地为PMU分配网络通信资源,减小PMU数据传输的时延和丢包率。
1.2 调度算法
目前已经存在一些经典的调度算法:先进先出(First In First Out, FIFO)、轮询调度(Round Robin, RR)[13-14]、加权循环(WRR)算法[15]等。在众多算法中,WRR算法由于引入权重来合理分配网络资源,其在调度的实时性和丢包率上的性能相对较好。
WRR算法为每个队列赋予一个权值,并设置相关的权重计数器。在进行调度前,将权重分配给对应的计数器,该计数器指定一轮中对应队列传输的数据包数量。如果一个队列发送一个数据包,则该队列权重计数器减1。继续发送数据包,直到计数器达到零或者队列为空。最后,所有队列计数器都重置为其权重值。
当在WAMS中引入调度算法合理均衡地为PMU分配网络通信资源时,有两个特性是调度的依据:PMU采样频率和2)PMU数据包的大小,因此在网络资源有限的情况下,如何根据以上两个特性合理设计调度算法是本文的重点。
2 SAWRR算法
结合WAMS中PMU采样频率和数据包大小特性,本文提出了一种基于采样感知的加权循环调度算法SAWRR。
2.1 权重的设计
在WAMS中,PMU收集并传输实时广域同步数据,它的采样频率基本在50到150之间,其数据用于监测电力系统的动态安全性。由于PMU的采样频率会影响数据传输的效率,而在WRR算法中权重的确定尤为重要,所以通过采样频率来计算权重,能够对PMU的数据进行比较好的调度。
其中:Wi是队列i的WRR权重,samplei是队列i的采样频率,N是总的队列数。在WAMS中,WRR算法会造成队列中多个数据包延迟。在队列长度有限的情况下,累计延迟的数据包会溢出队列,最终会导致数据包丢失。
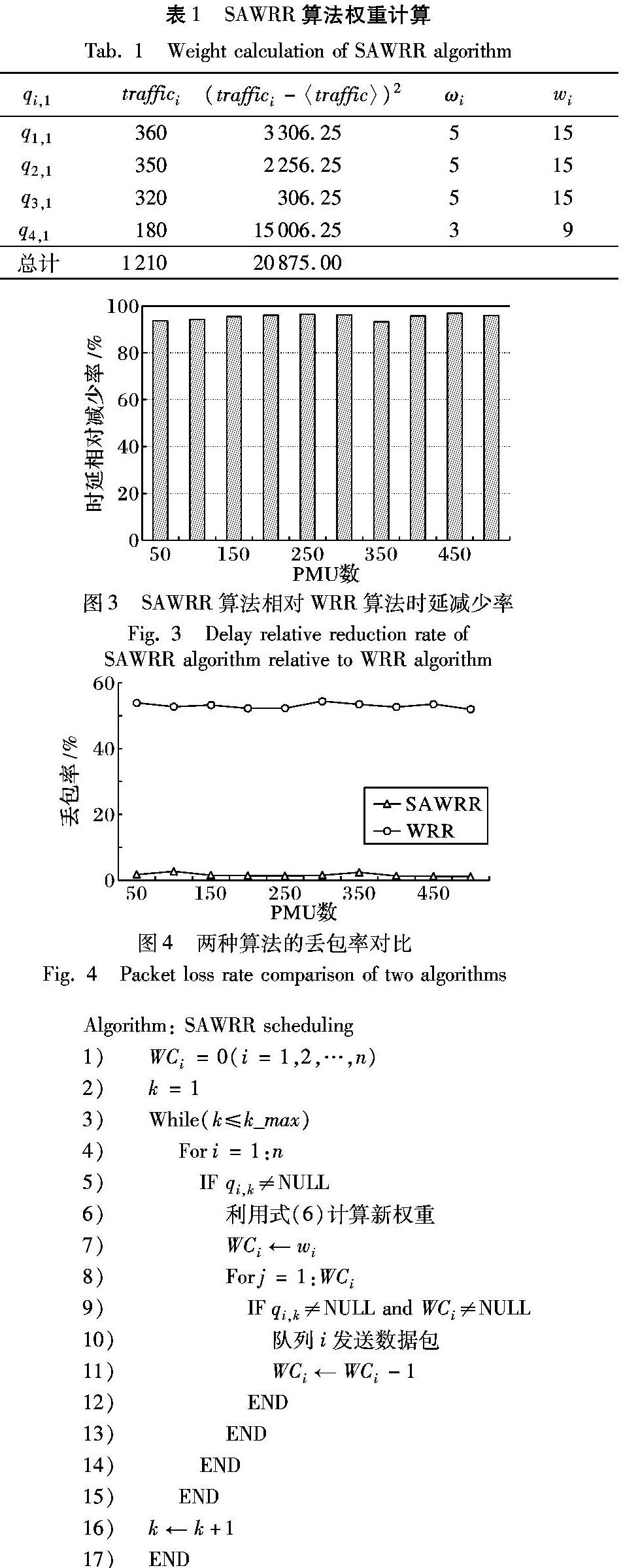
如图2所示,在权重为3的情况下对4个队列q1、q2、q3和q4进行一轮调度时,虚线框表示被调度送出队列的数据包,实线框表示队列中剩余的数据包。其中,队列q1剩余数据包量最多。随着PMU采样的数据包不断进入队列和WRR调度的持续,q1的滞留数据包增加,其调度时延也相应增加,队列最终因延迟数据包累计而装满,导致数据包丢失。
为了解决电网中调度的上述问题,需要结合采样频率和数据包大小重新定义权重。该权重计算主要有以下两个步骤:
第一步 多个PMU业务流量归一化。根据PMU采样数据包来确定当前多个PMU业务流量的均方差,以判定当前多个PMU业务流的离散程度。
假设每轮进队列i的标准数据包大小为size_standardi,业务流为traffici,则:
第二步 确定新权重wi。由第一步可知β值越大说明当前多个PMU业务流差异比较大,多个业务流的调度权重也要相应调整,此时需将带宽划分的模块减小,资源分配才越均衡; β值越小说明当前多个PMU业务流差异较小,业务流量较均衡,多个业务流的调度权重也应接近;但当β<1时,需要加1避免产生大的量化误差[16],因此权重调整系数ωi可以定义如下:
然后通过系数ωi来调整当前权重,为每个队列产生适当的权重:
2.2 SAWRR算法
根据上面权重,设计SAWRR算法。算法伪代码如下。
步骤1 参数初始化。
定义队列数量n,第k轮队列i的数据包数为qi,k,队列i的权重为wi,队列i的权重计数器为WCi,循环轮数k,最大循环轮数k_max。
步骤2 进行队列数据包的调度。
先确定队列是否为空,如果不为空,则根据式(6)确定wi,将每个队列的权重赋给对应的计数器,如果一个队列发送一个数据包,则该队列权重计数器减1。继续发送数据包,直到计数器达到零或者队列为空。然后将计数器重置为对应的队列权重值,重复上述过程,直到队列为空。
当PMU的采样频率或者包的大小发生改变,由于式(6)的迭代计算,该算法可以根据PMU当前的采样来计算权重,因此,SAWWR算法可以自适应地感知PMU的采样变化,及时根据PMU新的采样频率和数据包大小调整调度算法中的权重。通过在图1的主站运行SAWRR调度算法,可以达到减少PMU采样数据包的排队时延。
表1显示的是基于图2中队列计算SAWRR算法的权重。
将表1中计算的权重用到图2的队列中进行调度,可以发现,与图2中运用WRR算法相比,SAWRR算法将延迟数据包的总数从6减小到0,传输效率明显提高。
3 仿真结果分析
为了分析SAWRR算法在智能电网PMU数据传输中对数据传输的高效性、完整性和及时性的影响,本文通过在Matlab中建立传输调度模型,仿真实现了SAWRR算法、WRR算法,并比较了上述算法在不同的PMU的数目下平均时延、丢包率、吞吐量三个方面的性能。根据电网WAMS中PMU采样频率和采样数据包大小,在仿真中PMU采样频率为50~150次/s随机分布,PMU采样数据包大小为60~80B随机分布。
图3显示了SAWRR算法相对WRR算法时延减少率。从图中可以看出,SAWRR算法的调度时延相对WRR算法减小少了95%左右。在PMU数目相同的情况下,SAWRR的权重是根据PMU采样频率和采样数据包大小确定的,通过SAWRR算法调度每轮输出的数据包数量比用WRR算法调度的多,数据包能够更快地被传输,因此通过SAWRR算法调度数据包的时延要比用WRR算法调度的时延小。
图4显示了两种调度算法下的丢包率的比较。从图中可以看出来,随着PMU数量增加,两个算法的丢包率都不会发生明显的变化,调度的稳定性较好;然而,SAWRR算法丢包率要低于WRR算法。在相同数目PMU的情况下,由于SAWRR可以自适应感知PMU采样变化而调整权重,所以用SAWRR算法调度时滞留的数据包较少,因队列缓存满而溢出丢包的情况也随之减少。
图5显示了SAWRR算法相对WRR算法吞吐量增加率。从图中可以看出来,通过SAWRR算法调度PMU数据包的吞吐量相比用WRR算法调度的吞吐量增加了210%左右。在相同数目PMU的情况下,因为每轮SAWRR算法传输的数据包比用WRR算法多,所以SAWRR算法的总吞吐量要比WRR算法多。
4 结语
本文针对WAMS中不同采样频率的PMU竞争使用有限的网络通信资源可能存在不均衡的问题,提出了一种基于电网PMU采样感知的SAWRR调度算法。该算法结合了PMU的采样频率和数据包大小两个特性定义了循环调度的权重,使调度的数据包得到高效的传输。由于权重的迭代计算,该算法可以自适应感知PMU采样变化,及时调整数据包传输。仿真结果表明,将SAWRR算法運用到PMU中数据包的传输中,能够增大数据包的吞吐量,减小数据包的时延和丢包率,从而保证数据传输的高效性、完整性和及时性,有利于智能电网的稳定性。在后续工作中将继续展开保证电网中数据高效传输的研究和设计。
参考文献 (References)
[1] 谢小荣,辛耀中.基于同步相量测量技术的广域测量系统应用现状及发展前景[J].电网技术,2005,29(2):44-49.(XIE X R, XIN Y Z. Present application situation and development tendency of synchronous phasor measurement technology based wide area measurement system[J]. Power System Technology, 2005, 29(2): 44-49.)
[2] 张恒旭,靳宗帅,刘玉田.轻型广域测量系统及其在中国的应用[J].电力系统自动化,2014,38(22):85-90.(ZHANG H X, JIN Z S, LIU Y T. Wide-area measurement system light and its application in China[J]. Automation of Electric Power Systems, 2014, 38(22): 85-90.)
[3] ARAVIND M N, ANJU L S, SUNITHA R. Application of compressed sampling to overcome big data issues in synchrophasors[C]// Proceedings of the 2016 IEEE 6th International Conference on Power Systems. Piscataway, NJ: IEEE, 2016: 1-5.
[4] ZHU X, WEN M H F, LI V O K, et al. Optimal PMU-communication link placement for smart grid wide-area measurement systems[J]. IEEE Transactions on Smart Grid, 2018, 10(4): 4446-4456.
[5] SARAILOO M, WU N E. A new PMU placement algorithm to meet a specified synchrophasor availability[C]// Proceedings of the 2016 Innovative Smart Grid Technologies Conference. Piscataway, NJ: IEEE, 2016: 1-5.
[6] GADDE P H, BISWAL M, BRAHMA S, et al. Efficient compression of PMU data in WAMS[J]. IEEE Transactions on Smart Grid, 2016, 7(5): 2406-2413.
[7] ZHANG F, CHENG L, LI X, et al. Application of a real-time data compression and adapted protocol technique for WAMS[J]. IEEE Transactions on Power Systems, 2015, 30(2): 653-662.
[8] 鮑兴川,彭林.智能配电网通信多信道调度策略[J].计算机应用,2018,38(5):1476-1480.(BAO X C, PENG L. Multi-channel scheduling strategy in smart distribution network[J]. Journal of Computer Applications, 2018, 38(5): 1476-1480.)
[9] 向敏,陈诚.基于改进Dijkstra算法的配用电通信网流量调度策略[J].计算机应用,2018,38(6):1715-1720.(XIANG M, CHEN C. Traffic scheduling strategy based on improved Dijkstra algorithm for power distribution and utilization communication network[J]. Journal of Computer Applications, 2018, 38(6): 1715-1720.)
[10] 薛禹胜,徐伟,DONG Z,等.关于广域测量系统及广域控制保护系统的评述[J].电力系统自动化,2007,31(15):1-5.(XUE Y S, XU W, DONG Z, et al. A review of wide area measurement system and wide area control system[J]. Automation of Electric Power Systems, 2007, 31(15): 1-5.)
[11] 鞠平.电力系统广域测量技术[M].北京:机械工业出版社,2008:9-24补充页码范围.(JU P. Power System Wide Area Measurement Technology[M]. Beijing: China Machine Press, 2008: 9-24.)
[12] 窦开明,祝鑫,马梦宇,等.IEEE同步相量相关标准的发展与比较[J].电气应用,2018,37(6):41-45.(DOU K M, ZHU X, MA M Y, et al. Development and comparison of IEEE synchronous phasor related standards[J]. Electrotechnical Application, 2018, 37(6): 41-45.)
[13] HAHNE E L. Round-robin scheduling for max-min fairness in data networks[J]. IEEE Journal on Selected Areas in Communications, 1991, 9(7): 1024-1039.
[14] SHREEDHAR M, VARGHESE G. Efficient fair queuing using deficit round-robin [J]. IEEE/ACM Transactions on Networking, 1996, 4(3): 375-385.
[15] KATEVENIS M, SIDIROPOULOS S, COURCOUBETIS C. Weighted round-robin cell multiplexing in a general-purpose ATM switch chip[J]. IEEE Journal on Selected Areas in Communications, 1991, 9(8): 1265-1279.
[16] ITO Y, TASAKA S, ISHIBASHI Y. Variably weighted round robin queueing for core IP routers[C]// Proceedings of the 21st IEEE International Performance, Computing, and Communications Conference. Washington, DC: IEEE Computer Society, 2002: 159-166.

