基于神经网络方法的井下机械钻速研究
刘维凯,徐 文
(东北石油大学 石油工程学院, 黑龙江 大庆 163000)
从现在的技术水平看,非石油资源的利用仍然处于初级阶段,在未来一段时间内,石油资源的战略地位依然不可取代。作为整个石油行业的龙头,钻井工程对于油气勘探开发起着关键性作用,是发现油气藏、提高采收率、提高经济效率的重要保证。因此只有不断提高钻井水平,才能实现高效、快速钻井。钻井速度是整个钻井工程的核心问题,提高钻井速度是钻井工作人员重点研究的问题。因此,在钻探过程中,对钻井速度进行科学预测与计算就成为实现智能化钻井的一项重要内容。
目前,常见的预测机械钻速的方法主要是依靠以往的经验公式结合现场数据直接统计出机械钻速[1]。Mourer W C根据室内单齿实验提出井底净化充分的钻速模式[2];1969年Young F S提出杨格模式;1970年Amoco根据现场数据提出普遍二维钻速模式,即钻速与转速和钻压的指数函数成正比,在不同地层采用不同的转速指数和钻压指数[3];1974年Bourgoyne A和Young F S运用多元回归分析法,根据钻压、转速、井底压差、岩石特性、井深和水力参数等主要因素对钻速的综合影响,建立多元钻速回归方程[4];20世纪80年代,辽河油田等单位在研究外国钻井模式的基础上,与石油勘探开发研究院开展试验研究工作,建立四元钻速模式;1989年以来,大庆油田和大庆石油学院共同研究试验,通过大量现场试验,应用模糊决策理论和可靠性优化理论,建立牙轮钻头多元随机钻速模式;苏联研究员布列多夫在分析研究成果的基础上,提出钻头工作数学模式[5]。全世界目前都研究出了很多机械钻速方程,但这些方程中所包含的大部分系数都会随着地层情况的变化而变化,而且很多实验方法都局限在室内,工作量巨大的同时准确性受到了影响。本文提出使用人工智能神经网络中的BP算法对机械钻速进行预测计算,可以大大的改善原有方法的不足,提高预测精度[6]。
1 影响钻井速度的主要因素
1.1 钻压对钻速的影响
钻压是影响钻速最明显因素之一。在以下实验条件下:①井底净化条件一定;②岩石破碎以机械破碎为主。钻压和钻速近似于线性关系。
Vm∝(W-M)
(1)
式(1)中,Vm为钻速,m/h;W为钻压,t;M为门限钻压,kN。
1.2 转速对钻速的影响
钻压和转速之间是以指数函数的关系变化的,关系如下。
Vm∝Ne
(2)
式(2)中,N为转速,r/s;e为转速指数。
实验证明,转速指数一般在0.5~1.0之间变化,随着岩石深度增加,转速指数逐渐下降。
1.3 钻头牙齿磨损对钻速的影响
钻井过程中,随着钻头破碎岩石的同时,钻头牙齿也会受到磨损,使钻头工作效率下降,钻速也随之降低。
(3)
式(3)中,C2为牙齿磨损系数;h为牙齿磨损量。
1.4 流量对钻速的影响
1.4.1 水力净化与井底水功率的关系
1975年阿姆科研究中心研究出了钻速与流量之间的关系。
(4)
式(4)中,CH为水力净化能力;Nc为实际比水力功率,kW/cm2;Ncr为净化充分时需要的比水力功率,kW/cm2;Vpcs为净化完善时的钻速,m/s。
1.4.2 钻速与井底水功率的关系
水力破岩的效果由门限钻压的变化体现,门限钻压中的水力破岩体现了水力破岩效果。但在实际操作时,水力的清岩和破岩作用是同时发生的,很难具体说明水力清岩和破岩的具体效果。因此,国内研究学者通常采用水力可钻法表示比水功率与钻速之间的关系。
Vm∝Ncf
(5)
式(5)中,f为地层水力指数,与地层等因素有关。
自从我国“六五”优选参数钻井技术开展以来,一些油田通过实验与统计回归分析相结合,得到了分井段的地层水力指数值[7]。其中胜利油田通过实验得出了地层水力指数和地层可钻性之间的关系。关系式如下:
f=0.701 1-0.056 82Kd
(6)
式(6)中,Kd为地层可钻性级值。
2 现有钻速方程模式分析
钻进过程中,钻进的速度会受到多种因素的影响,这些因素分为可控因素和不可控因素。可控因素包括:钻压、转速、牙齿磨损、水力因素和钻井液性能等;不可控因素包括所钻地层的岩石特性、地层压力等。在实际钻进过程中,根据现场客观规律,优选不同的参数进行配合,达到最佳的钻进效果[8]。
2.1 井底净化充分的钻速模式
该模式是莫勒在室内通过单齿实验建立的。实验测得岩石破碎体积(Vc)与钻压(W)成正比,而与岩石的抗压强度(σ)的平方成反比。钻速模型为:
(7)
式(7)中,K为地层可钻性系数;N为转速,m/s;Dh为钻头直径,mm。
这就是井底净化充分的钻速模式,目前现场应用不多。
2.2 修正杨格模式
钻速模式为:
(8)
式(8)中,Kf为地层可钻性系数;Cp为压差影响系数;CH为水力净化系数;M为门限钻压;C2为牙齿磨损因数;h为牙齿磨损量;当岩层特性、泥浆性能、钻头类型和水力参数一定时,Kf、Cp、CH、M、C2、h这6个参数都是常量,可由实验和资料确定,因此本模式也被称为“六参数钻速模式”。
在此模式中,地层因素对于钻速的影响主要体现在门限钻压和地层可钻性系数上。而对于可钻性系数,还包括了其他不确定因素对于钻速的影响,这些因素只能通过现场测量和室内试验确定,这显然是不合适的。因此本模式只是在理论上探讨而没有被用于实际现场。
2.3 苏联钻速模式
苏联研究人员认为,钻速模式采用积分和微分的综合模型更合理,在分析总结成果的基础上,提出了钻头工作数学模式。表达式为:
(9)
φ=φ0WqNq1
(10)
(11)
(12)
式(9)~(10)中:φ为机械钻速下降速率;V为机械钻速,m/s;Tt,Tb分别为钻头牙齿和轴承寿命;φ1,r1为常量;φ,r为与钻头结构、泥浆性能和岩石机械性能有关的系数;n、φ0为系数,给定条件下为常量。
这就是钻速的微分模式。特定是根据机械钻速下降速率来估计牙齿的磨损,使用变分法求解。但本模式待定系数较多,需要通过大量的实验来确定。
3 钻速实验及数据处理
如何正确利用钻井数学模式,除取决于客观规律外,还需要正确的基础数据。因此,优选和收集实钻资料就成为钻井中不可缺少的一环。处理钻井资料的目的在于:排除钻进时随机数据的影响;对统计数据进行删选整改,提取能真实反映地层情况和符合基本钻进规律的数据,使钻井设计更加合理。
3.1 释放钻压法
钻井过程中,钻柱的钻井是靠钻柱的弹性变形实现,起下钻的过程就是补充弹性变形能的过程。
在钻井过程中,如果停止钻进,累积的弹性变形能就会逐步释放出来,就可以获得钻压与钻速的关系。由于在钻柱弹性变形能释放的过程中,钻压减小,大钩悬重增加,因此这种方法也叫悬重恢复法。该法最大的优势在于测量是动态进行的,测量得到的数据都是井下实时的钻压和钻速,使结果更准确[9]。
在弹性变化范围内,应力与应变关系为:
△σ=E△ε
(13)
应力与应变变化值为:
(14)
(15)
钻速为钻柱伸长量与时间之间的关系:
(16)
考虑钻杆与钻铤以及单位换算,钻速最后表示为:
(17)
式中:△W为钻压变化值,s;△T为钻压下降 所需时间,s;lt为钻杆长度,m;lc为钻铤长度,m;Ac,At分别为钻铤,钻杆截面积,cm2;E为钢材的弹性模量。
3.2 实验步骤
1)先用正常钻压和转速钻进,记录钻压下降10%所需时间△t,然后增加钻压到原钻压的20%,钻进2△t的时间,形成新的钻进痕迹。
2)保持其他参数不变,记录钻压由初始钻压减小到某瞬时时刻的时间和钻压值,直到钻压下降到原钻压的50%左右。
3)改变转速,其他参数不变,重复上述实验。
3.3 数据处理
每一组转速一共有n+1个试验点,包含n个间隔段,进行数据处理:
平均钻压:
(18)
钻压差值:
△Wi=Wi-1-Wi
(19)
各井段时间:
△Tij=Tij-Ti-1,j,其中i=1,2,3…n,j=1,2
(20)
转速1下的各段钻速:
(21)
转速2下的各段钻速:
(22)
转速1下的门限钻压M′:
(23)
转速2下的门限钻压M″:
(24)
实验地层门限钻压为:
(25)
根据不同实验结果,平均转速指数为:
(26)
数据处理时,两组门限钻压的误差值小于20%为合格。否则补做一组或两组实验,直到误差小于20%[10]。
4 神经网络BP算法
通过以上对几种钻速方程模式的分析可知,在钻井过程中,没有一种钻速方程可以准确、定量的得到实时钻速,因此提出使用人工智能神经网络解决这一问题。
4.1 BP算法
BP算法的学习过程是由信号的正向传播与误差的反向传播两部分组成。正向传播是将输入样本从输入层输入,经隐层处理后,传向输出层。如果输出层的实际输出和期望的输出不符,则进行误差反向传播。误差反传是将输出误差通过隐层传回输入层,并同时将误差信号分给各层中的各个单元,获得各层单元的误差信号,用来修正各单元权值。这种正向传播与反向传播调整权值是周而复始地反复进行的。最终的目的是得到可接受的误差,使输出接近期望值[11]。
目前应用最广泛的神经网络就是采用BP算法的多层感知器,而其中最普遍的就是单隐层网络。一般将单隐层网络感知器分为3层,包括:输入层、隐层和输出层。每层都有若干神经元,且之间相互独立,互不干扰。本文中,输入层用来输入与钻速大小相关的数据,例如:钻压、转速、水力参数、钻井液性能等;输出层输出通过以上参数预测出的钻速值;隐层用来预测钻速和误差。
4.2 BP算法的改进
BP算法中的3层感知器,可以使结果无限接近任何非线性函数的值,但在应用中仍然有不少缺陷:①训练形成局部极小得不到全局最优;②训练次数过多会使学习效率低,收敛速度慢;③隐节点选取错误;④新增加样本会遗忘旧样本[12]。
现提出一种改进方式:自适应调节学习率η,使其该大时增大,该小时减小。设初始学习率η,若经过一批次权值调整后总误差增大,则本次调整无效,且η(t+1)=βη(t);若经过一批次调整后总误差减小,则本次调整有效,且η(t+1)=θη(t)。这种方式可以合理控制迭代次数,提高BP算法收敛速度。
5 井下模拟算法训练
根据构建的BP神经网络,对给定的样本空间进行训练。确定为3层,第1层为输入层,4个节点;第2层为隐层,多个节点;第3层为输出层,1个节点[13]。
5.1 预测钻速
5.1.1 程序初始化
设输入向量为X=(x1,x2,…,xi,…,xn)T,隐层输出向量为Y=(y1,y2,…,yj,…ym)T,输出层输出向量为O=(o1,o2,…,ok,…ol)T,期望输出向量为D=(d1,d2,…,dk,…dl)T。
对于输出层:
ok=f(netk)k=1,2,…,l
(27)
(28)
对于隐层:
yi=f(netj)j=1,2,…,m
(29)
(30)
对于以上两式, 均为Sigmoid函数
(31)
f(x)具有连续、可导的性质,式(27)~(31)共同构成BP算法3层感知器的数学模型。
5.1.2 模拟数据确定及网络训练
根据前文内容,井下实时机械钻速与钻压、转速、钻头牙齿磨损、水力参数、钻井液性能、井深、地层物性等因素有关。上述这些参数可以用xk(=1,2,……)表示。通过上述研究,应用BP神经网络可以构造出基于人工智能机械钻速计算模型:
vpi=f(ΣWf(ΣVxki))
(32)
通过之前对于BP算法的改进,调节输入层与隐层、隐层与输出层之间的阈值和权值,进行模拟计算使得到的钻速值与期望值之间的误差变得无限小,接近于零[14]。
5.2 模拟计算及结果分析
5.2.1 模拟计算
为了验证通过BP神经网络计算钻速的可靠性,选择钻头深度、钻压、转速和流量作为实际参数组成样本空间,见表1。
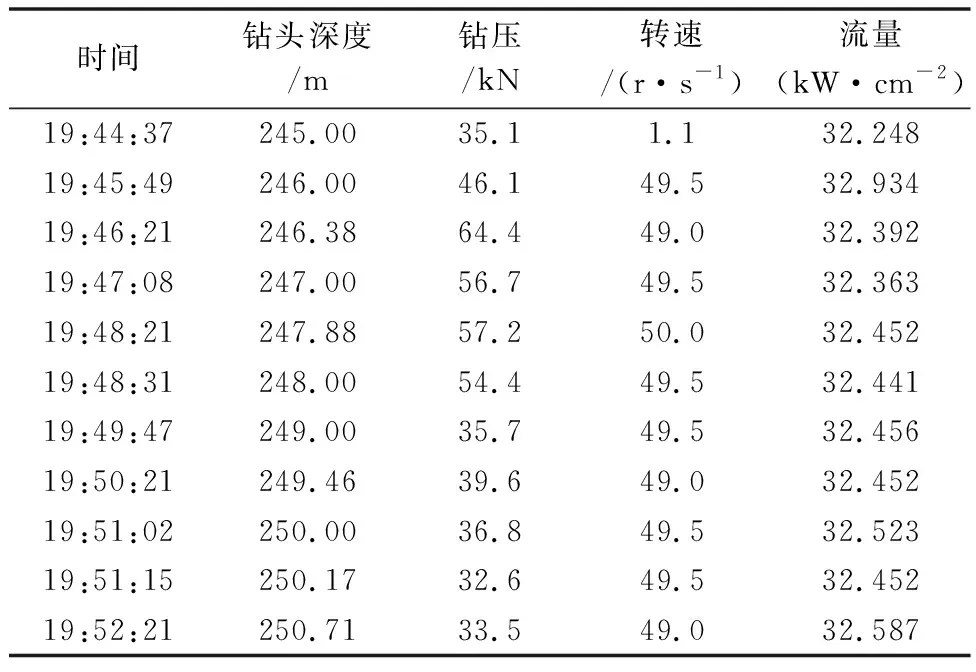
表1 某井钻进时各钻井参数
根据本文理论与编写的计算程序,对表中数据进行模拟,模拟结果如图1所示。
5.2.2 误差分析
1)算法研究不够深入透彻,导致计算时收敛慢、误差较大。
2)没有完全掌握成熟的智能钻井技术,不容易得到真实的随钻数据,样本中部分数据有误差。
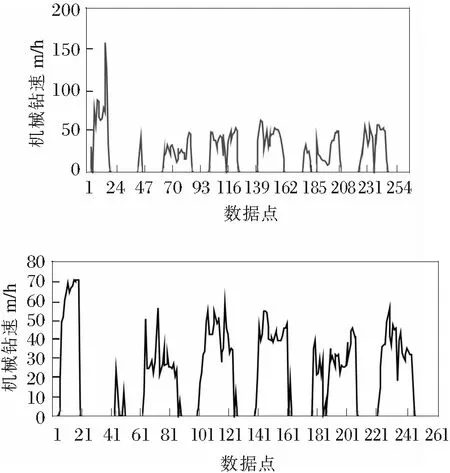
图1 测量数据与模拟数据对比
6 结 语
1)钻压、转速、水力参数、地层可钻性、牙齿磨损等对钻速都会产生明显影响 ,现有的几种常用的钻速方程并不适用于井下钻速预测。
2)通过神经网络BP算法的研究,编写计算软件,进行模拟计算,可以实现井下机械钻速的预测。
3)目前通过BP算法预测井下钻速的研究还处于初级阶段,存在一些问题,但随着科技的进步,研究的进一步加深,该算法将更加完善。

