多假设多目标跟踪算法

王 岩，蒿兴华，杨顺云

（解放军31108 部队，南京 210016）

多假设多目标跟踪算法（MHT）是非常经典的多目标跟踪算法，由Reid 在对雷达信号的自动跟踪研究中提出，本质上是基于Kalman 滤波跟踪算法在多目标跟踪问题中的扩展。定义在k 时刻之前的检测为Zk，多假设跟踪的目标是基于已有轨迹对这种观测关联进行条件概率建模，把似然关联假设Θik 划分为当前关联假设Θi（K）和k-1时刻的假设集合Θik（m）。可以利用贝叶斯推理得到关于关联假设的后验概率公式。

其中公式右侧第一项表示基于前期假设集合和当前假设的观察似然概率，即在历史关联的基础上，当关联Θivartheta_{I}（K）成立时，表现出当前观测Z（k）的概率；第二项表示当前假设的似然概率，即在历史关联的基础上，当前关联假设的概率；第三项表示前期假设集合后验概率。c 是贝叶斯公式中的分母，对于当前观测已知的条件，可以认为是一个常数。总体的假设后验概率可以表示为此三项的乘积。而公式第三项表示k-1时的后验概率，因此，只考虑第一项和第二项就可以得到一个递推公式。

如何对第一项和第二项进行建模？MHT 采用了二个概率模型：用均匀分布和高斯分布对关联对应的检测观察建模；用泊松分布对当前假设的似然概率建模。

前者表示，当观测是来自一个轨迹T 时，它符合T 的高斯分布，否则观测是一个均匀分布的噪声。后者表示，在误检和新对象出现概率确定的情况下，出现当前关联的可能性可以通过泊松分布和二项分布的乘积表示。在以上假设下，关联假设的后验分布是历史累计概率密度的连乘，转化为对数形式，可以看出总体后验概率的对数是每一步观察似然和关联假设似然的求和。因此，选择最佳的关联假设，转化为观察似然和关联假设似然累计求和的最大化。在进行具体实现和优化的时侯，I.J.Cox 等人提出了一种基于假设树的优化算法，如下图所示。

图中：左图为k-3时刻三个检测观察和两条轨迹的可能匹配。对于这种匹配关系，可以继续向前预测两帧，如图右。得到一种三层的假设树结构，对于假设树根枝干的剪枝，得到k-3时刻的最终关联结果。

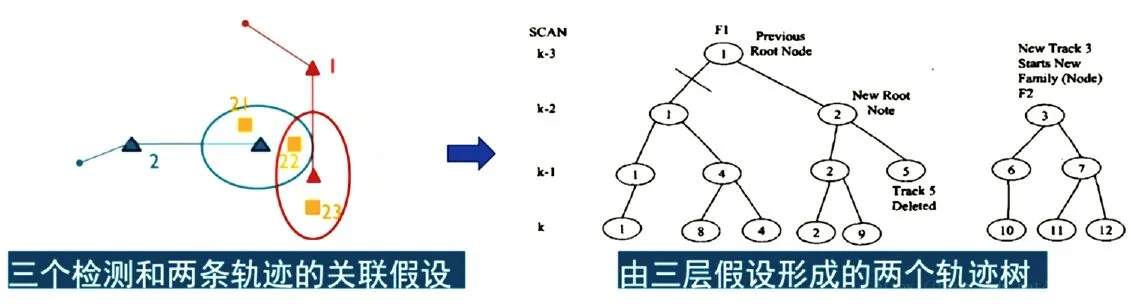
对于k 时刻的关联对数似然概率，可以认为是k 时刻之前关联观察似然概率的对数求和，由于任何时刻都可能存在多种假设关联，因此到k 时刻的假设构成了一种组合假设树的层次关系。例如图中左边表示的是2个轨迹和3个观测之间可能形成的关联假设，可能存在的假设有{观测23=＞轨迹1，观测22=＞轨迹2，观测21=＞新轨迹}或者{观测22=＞轨迹1，观测21=＞轨迹2，观测23=＞新轨迹}，因此产生2个假设分支。图中右侧是从这2个关联假设出发的三层假设树关系，可以看出随着假设层数的增多，关联假设出现组合爆炸的可能。因此进行必要的剪枝减少假设空间的数目是必须的步骤。那么如何选择最佳的关联呢？I.J.Cox 采用了2个步骤来实现。首先，限制假设树的层数为3层。其次，是对每个分支的叶节点概率对数进行求和，最大的分支进行保留，即选择边缘概率最大的那个分支假设作为最后选择的关联。

采用基于均匀分布、泊松分布以及高斯分布的模型，可以高效快速计算选择k-3时优化的假设关联。这种基于似然概率对数累加的方法虽然方便迅速，但是存在一个主要的限制，即假定观测关联符合高斯模型，并且在每一步选择关联假设之后，需要利用Kalman 滤波更新轨迹状态。通过对MHT 基本公式的扩展，可以建立不同的概率模型描述这种多假设关联的全局概率，例如Kim 等人在ICCV2015和ECCV2018通过归一化的最小均方差优化算法引入表观模型来扩展MHT 算法，取得不错的多行人跟踪结果。