一种动态创建和删除节点的神经网络算法*
李齐民
(中国地质大学 武汉 430074)
1 引言
BP神经网络,由于它的网络架构较为简单,算法实现较为容易,现已成为应用最广泛的神经网络模型之一[1]。为了获得更好的实验结果,在BP神经网络中,超参数的调整相对来说会一定的影响其训练结果[2~3]。对于神经网络隐含层神经元的数目的参数调整,除了基于经验的设置神经元数目外,还提出了动态结点创建(Dynamic Node Creation)的方法,随机地添加结点,然后进行训练。或者使用正交投影法(Orthogonal Projection Method)实现动态结点创建[4~5]。
相比于这一些方法,本文在动态结点创建的过程中,使用了一些临界条件使相应的神经元进行分裂或融合,这样既可以做到在动态创建结点的过程中不对训练结果产生负面影响,同时也不会导致由于产生过多的神经元而影响训练速度。
2 基于分裂与融合的动态结点创建方法
2.1 反向传播神经网络算法思想
反向传播算法是基于前馈神经网络的一种权重更新算法,我们定义神经元的输出为
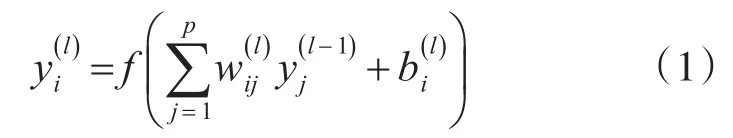
由此,我们可以有相应的权重和阈值的更新公式:

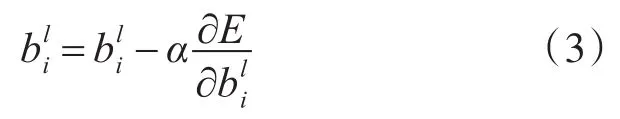
其中α为学习速率,E为样本的误差。
对于输出层的误差权重和阈值的更新公式,可以直接根据激活函数的导数得到结果。根据误差反向传播的思想,我们对于第l层的误差,可以将其转换为l+1层误差反向求和得到。通过导入数据集对神经网络进行反复地训练,可以得到训练完成的神经网络。
2.2 基于分裂与融合的动态结点的基本思想
在神经网络进行正向传播的过程中,如果神经元的个数是固定的,容易造成对训练集产生过拟合(神经元个数过多)或者欠拟合(神经元个数过少)的现象。而神经元的数量如果能在训练的过程中动态的增加或者减少,那么这样的现象就会相对缓解。但首先为了保证输出结果的正确,在结点创建的过程中神经元的输出不应当发生改变,不然会影响到网络之前训练的结果。
同时神经元的分裂仅会发生在隐含层当中,因此可以得到在第l层i个神经元发生分裂得到的等式为
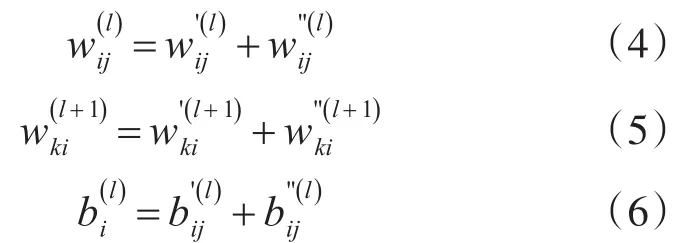
其中式(4)、(5)、(6)为分裂得到的两个神经元Node'与Node''与相应的连接权重和偏置的等式,为第l+1层第k个神经元与第l层第i个神经元的连接权重。
此时,对于新生成的神经元,可以使用随机数的方式直接根据原本的神经元生成相应的权重和偏置,即

为了防止生成的神经元出现权重过低的情况,其中R为服从标准正态分布的随机数。因而根据式(4),可以得到

式(5)、(6)可以根据式(4)到式(7)、(8)的推导方式得出相应的权重与偏置更新公式。
同样地,融合的方式则根据式(4)、(5)、(6)将两个神经元融合为一个神经元即可。
3 分裂与融合的神经元的选择
关于融合与融合的神经元的选择,我们可以考虑将表现最佳的神经元进行分裂,将表现较差的神经元之间进行融合。其中评判神经元好坏的方式,可以参考He等使用剪枝进行优化神经网络的方法[6],他们测试了多个衡量单个神经元重要性的指标,得出使用“onorm”进行评价的效果最好
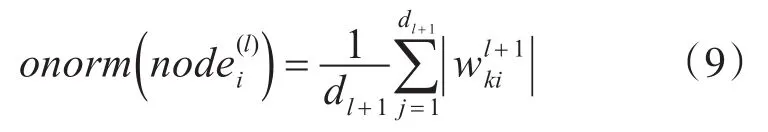
其中dl+1为第l+1层的宽度,即神经元的个数。
同时对于发生分裂和融合的判定方式,可以通过判断当前数据集的识别的误差与上一次识别的误差来确定,即识别误差降低则进行神经元的融合,识别误差升高进行神经元的分裂。
最后为了防止算法的进行过程中进行大量的分裂与融合,规定每训练一定量的数据集(如100)才进行一次判断。
4 测试结果
本文测试选取多种不同的数据集进行测试,在weka上进行代码的编写,其中学习速率为0.3,迭代次数为2000,隐藏层数仅一层,同时设定从1个神经元开始进行分裂与融合。得到表1的实验结果。
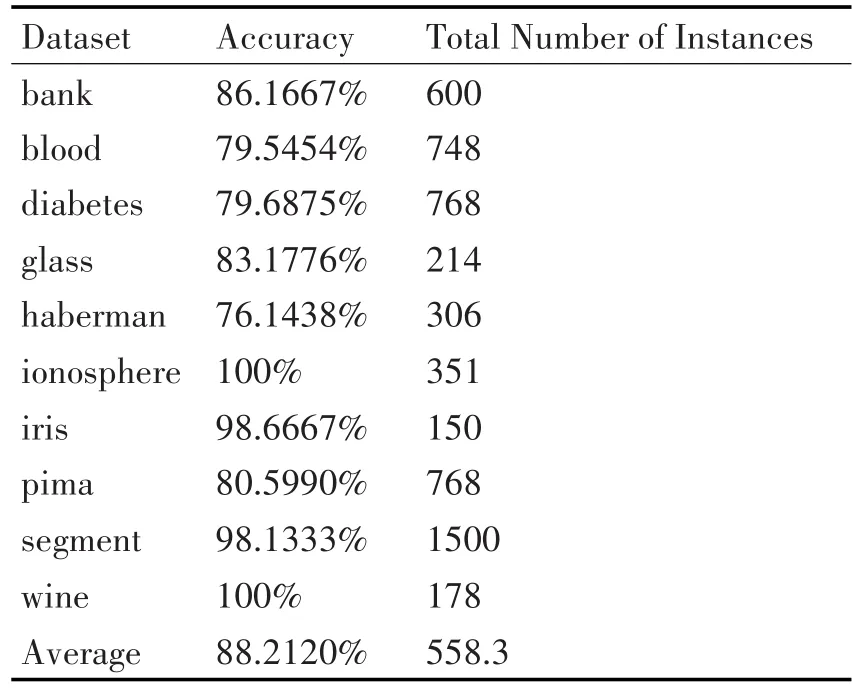
表1 算法测试结果
我们可以看到结果良好(88.2120%的平均正确率)。统计了在训练过程中的神经元的数量变化结果,可以得到如图1的实验结果。
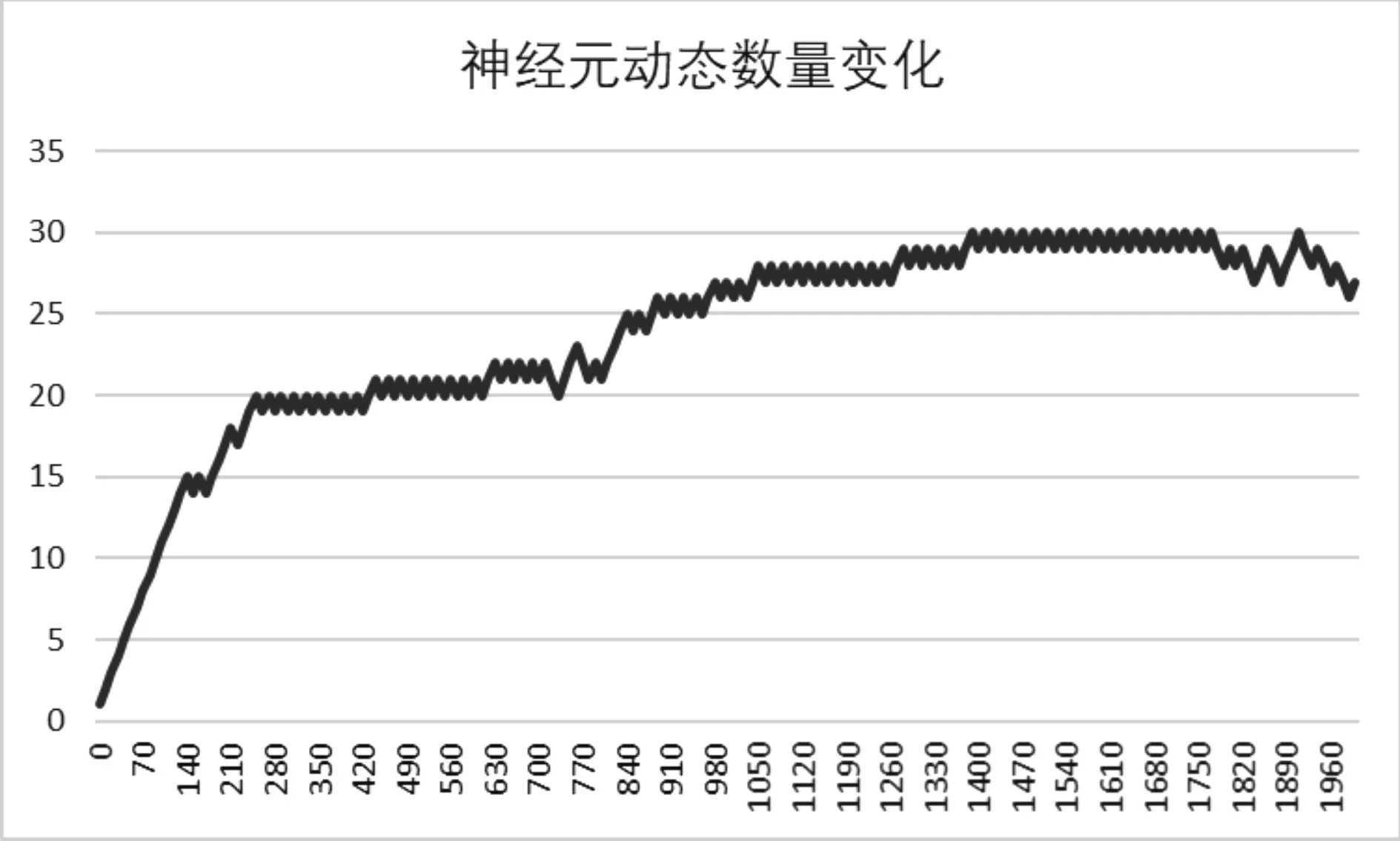
图1 神经元动态数量变化图
可以看到,经过一段时间的增长之后,神经元的数量趋向于稳定,不会出现神经元数量爆炸式增长的情况,同时识别正确率也处于一个比较高的状态。
5 结语
本文提供了一种对神经网络结点个数自动调整的一个方案,通过进行分裂与融合操作,使神经网络的结点数量可以根据情况动态的变化。该方法经过实验验证过后效果良好,因而可以考虑将其应用于各个领域中。

