基于字典学习的土壤地球化学数据稀疏重构
吴琳 魏友华 洪姗
摘 要: 在土壤地球化学数据的勘察和采集过程中,因为各种客观因素导致数据不完整,这会对后续的研究工作造成一定的影响,因此对数据进行重构是预处理阶段最基本的步骤。基于土壤地球化学数据在自身或在变换域内的稀疏性,建立基于字典学习的土壤地球化学数据重构模型,将数据重构问题转化为稀疏优化问题,可以减少数据重构后的平滑效果,在一定程度上保留土壤地球化学数据在异常区和背景区交界处的结构特征。最后将反距离插值法和稀疏重构算法重构后的数据进行对比,结果表明稀疏重构算法能有效地对土壤地球化学数据进行重构。
关键词: 土壤地球化学; 稀疏优化; 数据重构; 字典学习; 正交匹配追踪算法; 反距离插值法
中图分类号: TN911.1?34 文献标识码: A 文章编号: 1004?373X(2019)09?0018?04
Pedogeochemistry data sparse reconstruction based on dictionary learning
WU Lin, WEI Youhua, HONG Shan
(Geomathematics Key Laboratory of Sichuan Province, Chengdu University of Technology, Chengdu 610059, China)
Abstract: In the process of the exploration and collection of pedogeochemistry data, the data is incomplete due to various objective factors, which has the influence on the subsequent research to some extent. Therefore, the reconstruction of the data is the most fundamental step of pretreatment stage. On the basis of the sparsity of the pedogeochemistry data itself or in the transform domain, a pedogeochemistry data reconstruction model based on dictionary learning is established, which can convert the data reconstruction problem into sparse optimization problem, so as to reduce the smooth of reconstructed data, and reserve the structure feature of pedogeochemistry data at the junction of the abnormal area and background area to a certain extent. The data reconstructed by inverse distance interpolation method and sparse reconstruction algorithm is compared, which shows that the sparse reconstruction algorithm can reconstruct the pedogeochemistry data effectively.
Keywords: pedogeochemistry; sparse optimization; data reconstruction; dictionary learning; orthogonal matching pursuit algorithm; inverse distance interpolation method
0 引 言
在实际的地球化学数据采集中,常常因为采集区域地理环境条件的限制,采集方式、环境噪音等客观原因導致勘察收集到的数据不完整、不规则。而在地球化学数据异常圈定等各种处理中要求数据为标准的网格数据。另外,数据的不完整还导致信息的丢失,在后续的数据处理中会降低数据结果的可信度。因此,对实测数据的插值重构是地球化学数据处理的必要步骤。
地质学者们在地质数据插值过程中常用的方法为反距离加权插值法[1]、径向基函数插值法[2]、克里金插值法[3]、分形插值法[4]等。这些传统的插值方法均是将插值后的数据整体趋于平滑[5],会使土壤地球化学数据在背景区和异常区的交界处变得光滑,从而影响异常区域的波动。在此基础上进行下一步研究会影响地质人员对数据的分析,同时也会影响实地勘测找矿工作。因为在插值前并没有对实测数据进行降噪处理,所以使用传统方法进行插值重构后,得到的数据是对实测数据的近似插值重构,仍然会受到各种噪音的影响。
在图像处理领域,文献[6]提到降噪的同时会损失原始图像的纹理特征,因此提出基于稀疏表示的图像降噪算法,在降噪后可有效保留原始图像的结构信息。在土壤地球化学数据中,异常区与背景区之间的差异就类似于这种结构信息,在降噪时也需要保留这种结构信息。文献[7]在对地球化学数据的研究中指出,地球化学数据具有稀疏性,无噪声的土壤地球化学数据可以通过字典稀疏表示,与实际数据之间的逼近残差就是噪声,这样的降噪也不会使曲线光滑。
根据以上研究,本文尝试将稀疏表示应用在土壤地球化学数据重构中。对重构后的土壤地球化学数据进行异常圈定,再与反距离插值重构数据的异常圈定结果以及实际结果进行比较,最终数值实验模拟表明,该算法适用于土壤地球化学数据重构。
1 土壤地球化学数据稀疏重构模型
根据文献[8]提到的压缩感知理论的核心思想以及文献[7]指出的地球化学数据具有稀疏性可知,地球化学数据可以表示为:
式(5)是NP难问题,很难直接求解出该问题的精确解。本文采用贪婪算法中的正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法[10]近似求解这个问题。在实际应用中该算法的迭代过程如下:
2) 更新索引集[Vt=Vt-1?λt],記录找到的传感矩阵中的重建原子集合[At=At-1,aλt]。
3) 由最小二乘法得到[θt=arg miny-Atθ2];更新残差[rt=y-Atθt],并且令[t=t+1]。
4) 判断是否满足[t>K],若满足,则停止迭代; 若不满足,则执行步骤1)。
最后得到变换系数[Θ],这一过程又被称为稀疏编码。
为了更加精确地重构出数据,则要求设计出高效的观测矩阵和选择最能稀疏表达数据[X]的稀疏变换矩阵[Ψ]。本文只考虑稀疏变换矩阵[Ψ]。该矩阵要根据具体数据的特征来选择,适合于某一类数据的稀疏变换,不一定适合于另一类数据。因此选择K?SVD算法对稀疏变换矩阵[Ψ]进行自适应学习[11?12],从而达到能够适合于不同地区的土壤地球化学数据重构。
K?SVD每次更新一个原子(即变换矩阵的一列)及其对应的稀疏系数,并且需要将实际勘察数据分块。假设按照某种方式将数据分为[L]块,依次对稀疏变换矩阵第[ll=1,2,…,L]列进行更新:
1) 找出所有满足[wl=jθjl≠0]的数据小块[Yj];
2) 对每个下标[j∈wl],计算残差[elj=Yj-m≠lΦψmθmj];
3) 计算残差矩阵[El],其列为[eliji,j∈wl];
4) 对[El]进行奇异值分解得[El=UΔVT]。则[U]的第一列将作为字典更新后的第[l]列,同时更新[αliji,j∈wl]为[Δ1,1]乘以[V]的第一列。
每次迭代后会得到更新的稀疏变换矩阵[Ψ],直到达到最优的[Ψ]或达到设定的迭代次数。再重复稀疏编码和变换矩阵更新过程,最后得到重构的数据块,对其平均得到最终的重构数据[9]。
2 数值实验
为检验本文提出的基于字典学习的稀疏重构模型的效果,将其应用到实际土壤地球化学数据的插值重构中。在本文中,选择常用的高斯矩阵作为测量矩阵[13],选择DCT变换矩阵作为训练变换矩阵的初始矩阵[14]。根据土壤地球化学数据只有实际勘察数据这一特点,本文只能根据含噪数据对变换矩阵进行训练。
首先将数据对进行分块(本文中的块大小为[4×4]),把分块后的矩阵按列排列,则[M=16,N=25],变换矩阵的原子数[15][K=600]。采用本文的算法得到重构后的数据,对其平均即可得到最终的重构数据。
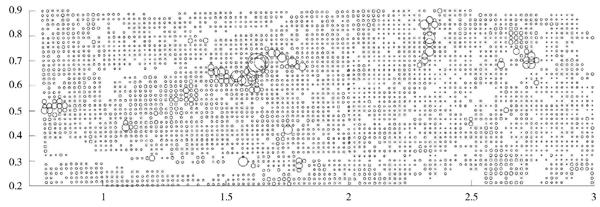
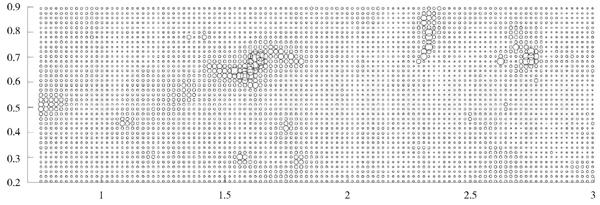
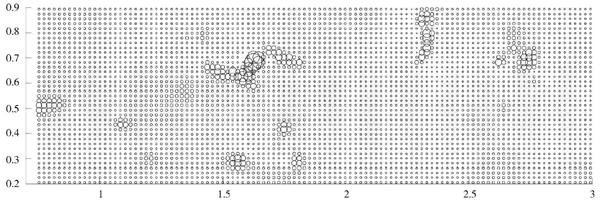
图1是原始缺失数据的散点图,图2为使用反距离插值法得到的数据散点图,图3为使用本文提出的稀疏重构模型得到的数据散点图。其中,图中圆圈越大表示元素含量越高;圆圈越小表示元素含量越低。
从图1~图3中可以看出,两种重构数据与原始数据的值分布比较一致。图2中,反距离插值重构数据在圈较大区域内,其元素含量比原始数据的值低,且增长缓慢,即较为严重地破坏了异常区与背景区交界处的结构;而根据稀疏重构算法重构后的数据在圈较大区域内与原始数据的元素含量值保持一致,与图2相比,减弱了对异常区与背景区交界处结构的破坏,能更好地保留土壤数据的原始结构和有用信息的完整性。
图1 原始数据散点图

图2 反距离插值数据的散点图

图3 稀疏重构数据的散点图

3 结 论
本文根据土壤地球化学数据本身或在变换域的稀疏性,将数据重构问题转化为优化问题,可对土壤地球化学数据进行很好的重构,并且重构后的数据符合原始数据的特点,从而保留了异常区和背景区交界处的数据结构等有用信息,在一定程度上有利于后期处理土壤地球化学数据。
参考文献
[1] 樊子德,李佳霖,邓敏.顾及多因素影响的自适应反距离加权插值方法[J].武汉大学学报(信息科学版),2016,41(6):842?847.
FAN Zide, LI Jialin, DENG Min. An adaptive inverse?distance weighting spatial interpolation method with the conside?ration of multiple factors [J]. Geomatics & Information Science of Wuhan University, 2016, 41(6): 842?847.
[2] ZOU Youlong, HU Falong, ZHOU Cancan, et al. Analysis of radial basis function interpolation approach [J]. Applied geophysics, 2013, 10(4): 397?410.
[3] 陈琳,任春颖,王宗明,等.基于克里金插值的耕地表层土壤有机质空间预测[J].干旱区研究,2017,34(4):798?805.
CHEN Lin, REN Chunying, WANG Zongming, et al. Prediction of spatial distribution of topsoil organic matter content in cultivated land using Kriging methods [J]. Arid zone research, 2017, 34(4): 798?805.
[4] PARSA M, MAGHSOUDI A, YOUSEFI M, et al. Multifractal interpolation and spectrum?area fractal modeling of stream sediment geochemical data: implications for mapping exploration targets [J]. Journal of African Earth Sciences, 2016, 128: 5?15.
[5] 朱钰,王伟,章传银,等.流动重力空间插值方法比较[J].测绘通报,2017(10):12?17.
ZHU Yu, WANG Wei, ZHANG Chuanyin, et al. Comparison on mobile gravity among different spatial interpolation methods [J]. Bulletin of surveying & mapping, 2017(10): 12?17.
[6] HAN Jin, JING Yue, ZHANG Yue, et al. Local sparse structure denoising for low?light?level image [J]. IEEE transactions on image processing, 2015, 24(12): 5177?5192.
[7] FELISA G, CIRIELLO V, ANTONELLINI M, et al. Data?driven models of groundwater salinization in coastal plains [J]. Journal of hydrology, 2015, 531: 187?197.
[8] 马坚伟,徐杰,鲍跃全,等.压缩感知及其应用:从稀疏约束到低秩约束优化[J].信号处理,2012,28(5):609?623.
MA Jianwei, XU Jie, BAO Yuequan, et al. Compressive sen?sing and its application: from sparse to low?rank regularized optimization [J]. Signal processing, 2012, 28(5): 609?623.
[9] ELAD M, AHARON M. Image denoising via sparse and redundant representations over learned dictionaries [J]. IEEE transactions on image processing, 2006, 15(12): 3736?3745.
[10] 马小薇.基于压缩感知的OMP图像重构算法改进[J].电子科技,2015,28(4):51?53.
MA Xiaowei. Improvement of OMP image reconstruction algorithm based on compressed sensing [J]. Electronic science & technology, 2015, 28(4): 51?53.
[11] 刘翠响,马玉双,王宝珠,等.过完备字典稀疏表示下的RAMP重构算法[J].计算机工程与应用,2018,54(14):199?202.
LIU Cuixiang, MA Yushuang, WANG Baozhu, et al. RAMP reconstruction algorithm based on overcomplete dictionary sparse representation [J]. Computer engineering and applications, 2018, 54(14): 199?202.
[12] 吴建宁,徐海东,王珏.基于过完备字典稀疏表示的多通道脑电信号压缩感知联合重构[J].电子与信息学报,2016,38(7):1666?1673.
WU Jianning, XU Haidong, WANG Jue. A new joint reconstruction algorithm of compressed sensing for multichannel EEG signals based on over?complete dictionary approach [J]. Journal of electronics & information technology, 2016, 38(7): 1666?1673.
[13] 党骙,马林华,田雨,等.[m]序列压缩感知测量矩阵构造[J].西安电子科技大学学报,2015,42(2):186?192.
DANG Kui, MA Linhua, TIAN Yu, et al. Construction of the compressive sensing measurement matrix based on [m] sequences [J]. Journal of Xidian University, 2015, 42(2): 186?192.
[14] 王强,李佳,沈毅.压缩感知中确定性测量矩阵构造算法综述[J].电子学报,2013,41(10):2041?2050.
WANG Qiang, LI Jia, SHEN Yi. A survey on deterministic measurement matrix construction algorithms in compressive sensing [J]. Acta electronica Sinica, 2013, 41(10): 2041?2050.
[15] 练秋生,张伟.基于图像块分类稀疏表示的超分辨率重构算法[J].电子学报,2012,40(5):920?925.
LIAN Qiusheng, ZHANG Wei. Image super?resolution algorithms based on sparse representation of classified image patches [J]. Acta electronica Sinica, 2012, 40(5): 920?925.

