基于小波去噪和神经网络的期货预测模型

张煌，梁朋，肖琨武，徐嘉蔚，施三支

（1.长春理工大学 理学院，长春 130022；2.长春理工大学 光电工程学院，长春 130022）

期货市场被誉为经济学中最理想的市场形式，是基于广大商品生产者、贸易商和加工商的广泛商业实践而产生的。国内期货市场在经历了方案研发初步实施阶段、迅猛发展阶段之后目前正处于整顿阶段，而由于期货交易的市场管理和风险评估能力不断得到提升，同时越来越多的投资者针对期货进行研究，整个市场的规范化得到了极大的改善。

沪深300指数样本覆盖了沪深市场60%左右的市值，具有良好的市场代表性、反映股市的综合变动，可以给投资者提供权威的投资方向。现如今国内许多学者针对沪深300股指期货也做了许多研究，建立不同的预测模型.其中阚子良，蔡志丹［1］提出了一种基于优化机器学习方法的股价时间序列预测方法。李鹏飞［2］利用ARMA模型与GRNN广义神经网络模型相结合对收盘价进行短期预测。张翱翔［3］利用BP神经网络选取四只股票来进行国内外股票价格预测。黄卿，谢合亮［4］，基于机器学习方法研究BP神经网络，SVM，与XGBoost对期货数据预测的影响。Esra Akdeniz［5］利用神经网络来分析非线性时间序列。Dingmu Cao，Wen Long，Wenning Yang［6］针对行业内指数进行相关性研究，发现指数出现周期性特征。

综上所述，可以发现前人对于沪深300指数的研究，虽然采取不同的方法，但是他们大多都是针对一种方法进行研究，也没有将他们所采用的方法与多种优化去噪方法相结合。因此考虑使用神经网络的方法，将Elman与BP两种神经网络模型对沪深300股指期货数据进行学习训练从而选出最佳的方法，再通过与小波去噪优化方法相结合从而建立最优的预测模型，对沪深300指数的开盘价，收盘价做出预测，得出结论。

1 小波去噪和BP神经网络原理

1.1 小波去噪原理

小波去噪原理如图1：

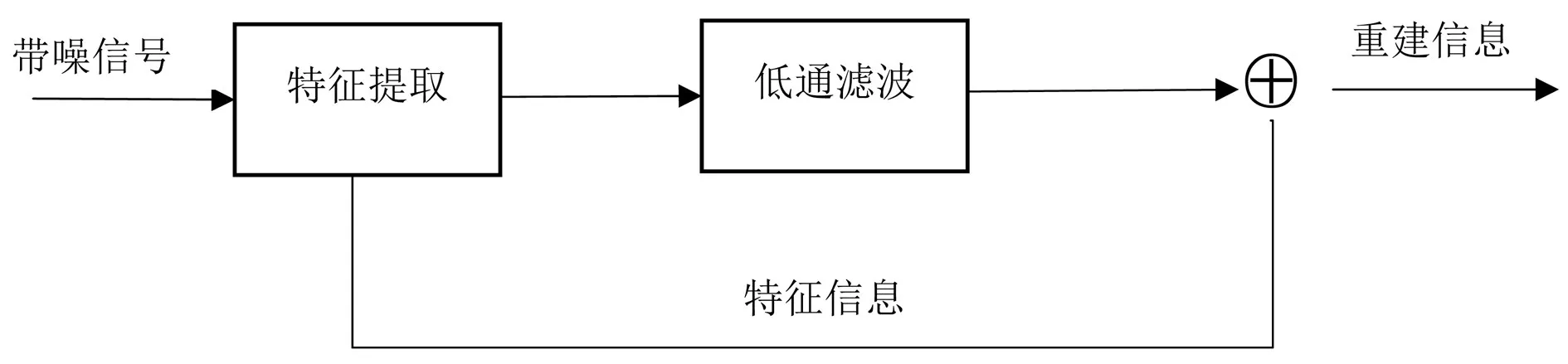
图1 小波去噪流程图

小波去噪源于傅里叶分析，可以沿时间轴前后平移，或按比例伸展和压缩以获取低频和高频小波，从而提取出已含噪声信号中的有用信号。一个含噪的模型可以表示为：

式中，f(k)为有用信号，S(k)为含噪声信号，e(k)为噪声，ε为噪声系数的标准偏差。

去噪的关键是在第二步中对小波系数进行去噪处理，根据处理规则的不同，小波去噪的常见方法可分为以下几类：1）模极大值去噪法；2）基于各尺度下小波系数相关性进行去噪（屏蔽去噪法）；3）小波阈值去噪法；4）平移不变量法；

在这里选择小波阈值进行去噪，其计算速度快，噪声能得到较好抑制，且代表原始信号的特征尖峰点能得到较好的保留。同时选取函数thselect获取阈值，利用DB4小波进行4层分解，对开盘价，收盘价进行消噪处理。

1.2 BP神经网络原理

BP神经网络最早由Rumelhart，McCelland等［7］科学家提出，BP神经网络学习过程由信号的正向传播与误差的反向传播两个过程组合，正向传播时，输入样本从输入层传入，经各隐含层逐层处理，传向输出层。若输出层的实际输出与期望输出不符，则转入误差的反向传播阶段。

反向传播时，将输出以某种形式逐层反传，并将误差分配给各层，将得到的误差信号作为修正各单元权值的依据。

神经网络示意如图2：

图2 神经网络示意图

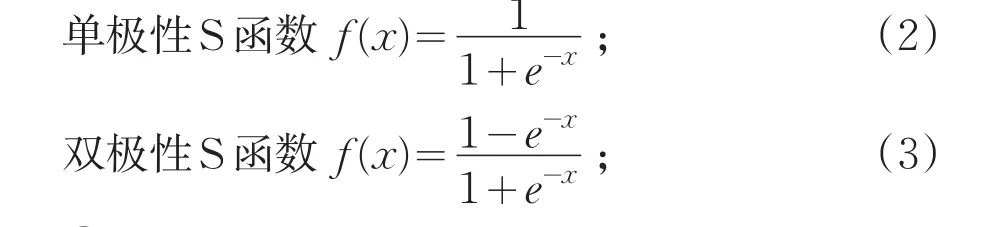
①网络初始化

赋予各连接权值（-1，1）内的随机数，设定误差函数e，此处设定均方误差为：

net.trainParam.goal=0.65*10^（-3）

②样本选取

选取k个输入样本以及对应期望输出；

③隐含层计算

④求偏导数

利用期望输出与实际输出，计算误差函数对输出层的各神经元的偏导数；

⑤修正权值

利用输出层各神经元偏导数和隐含层各神经元的输出修正连接权值；

⑥计算全局误差

在网络的设计上应注意针对网络的层数，隐层神经元的个数，初始权值，以及学习速率，期望误差进行选取。

2 沪深300股指期货的训练与学习

先选取2012年7月24日至2018年10月12日的沪深300指数期货的共1528个交易日的收盘价作为神经网络的学习数据，再分别利用Elman神经网络模型与BP神经网络模型通过Matlab软件进行分析，从而得到结果。

2.1 Elman神经网络的训练与学习

Elman神经网络又称SRN（Simple Recurrent Network）由Jeffrey L.Elman［8］提出，是最早的循环神经网络。Elman神经网络流程如图3：

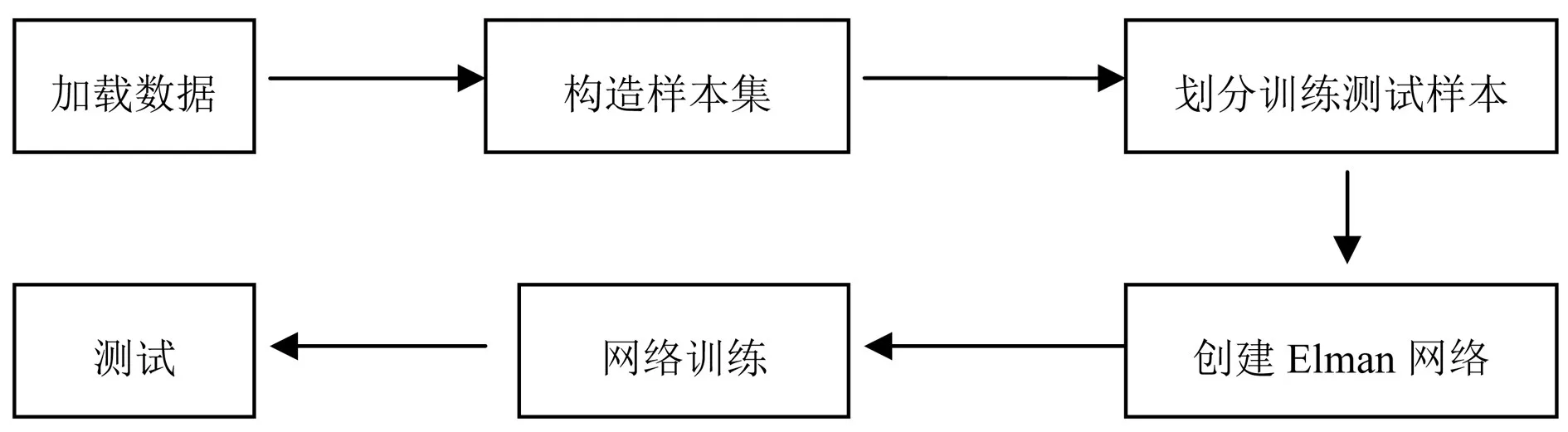
图3 Elman神经网络流程图

抽取相邻七天数据为一个样本，其中前六天设为自变量x，第七天为目标函数值y，将前1400个数据作为训练集，后122个数据作为测试集。

先将训练集代入建立的Elman神经网络模型中进行学习，再进行预测，并与已知的测试集进行比较得出误差分析。选择的各层神经元个数为：

输入层：6个；隐藏层：15个；输出层：1个，迭代次数为2000次。

训练集的真实值与预测值差距如图4所示：

图4 训练集的真实值与预测值折线图

训练集的真实值与预测值的局部放大图如图5所示：

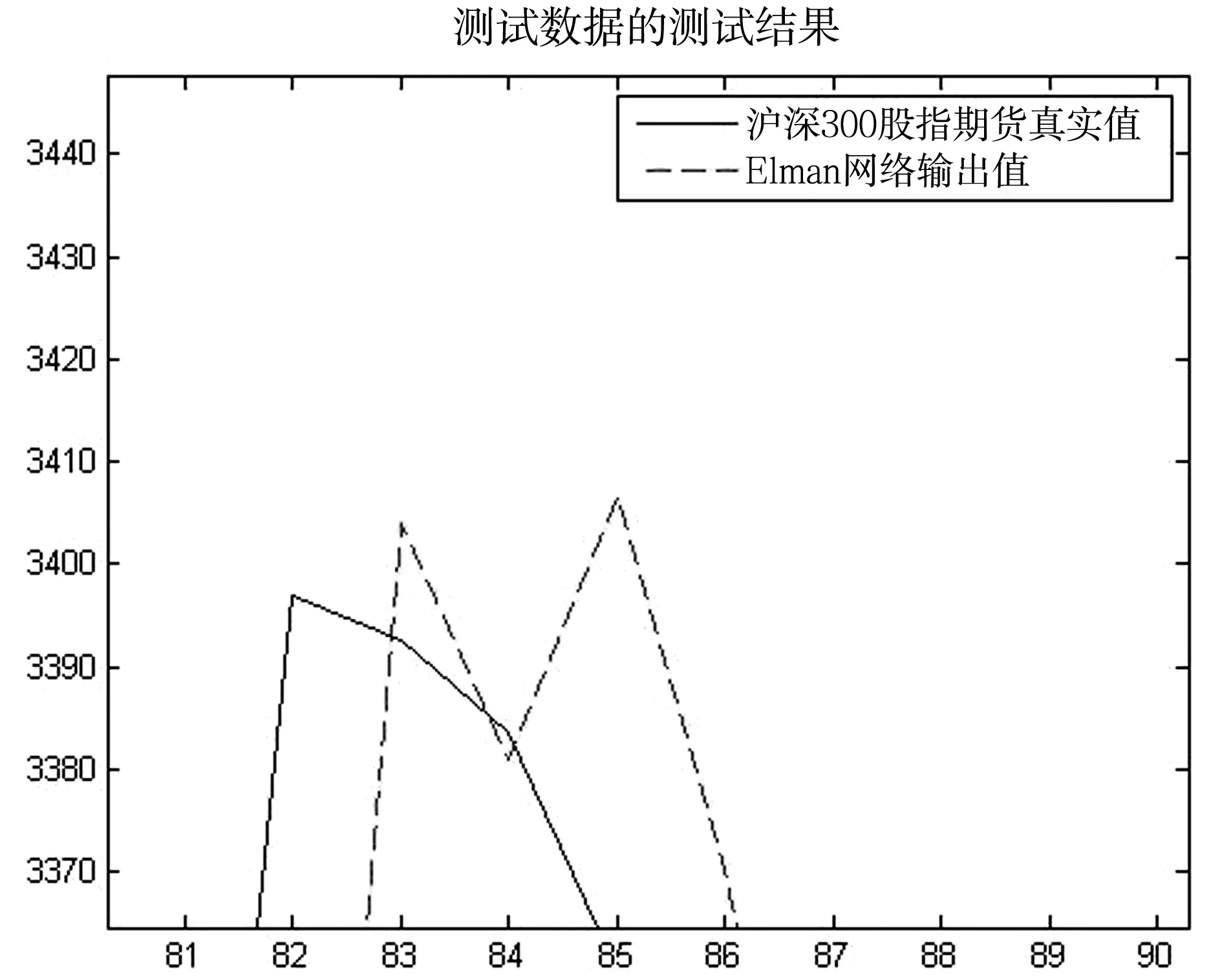
图5 训练集的真实值与预测值的局部放大图

由图5可见，网络对数据的拟合效果不是很好。网络实际输出与真实值的均方误差值mse=37.1。再将测试集输入网络，得到网络实际输出与真实值的均方误差33.6，该值虽然比训练集要低的多，但误差还是非常大。

测试集真实值与预测值的差距如图6所示：

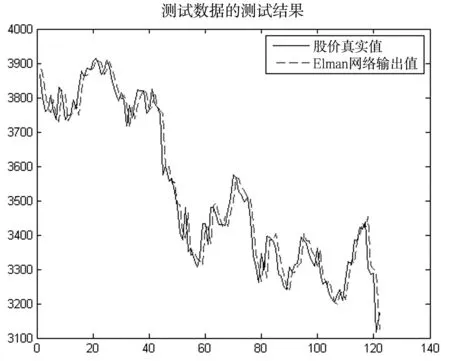
图6 测试集的真实值与预测值

测试数据测试结果的残差如图7所示：

图7 测试集残差

因此，继续对Elman网络的神经元的个数以及迭代次数进行多次调试，得到当神经元个数为40，最大迭代次数为4300次时效相对误差相对减少，此时训练集的真实值与预测值的相对均方误差mse=22.8，选取最后2天的预测结果与实际对比，显示如表1所示：

表1 Elman预测显示表

由得出的预测值与实际值的误差结果来看，此模型虽具有一定的预测能力但是仍达不到理想数值，因此继续对另外一种神经网络进行尝试。

2.2 BP神经网络的训练与学习

首先利用BP神经网络模型对1026个数据进行学习，选择恰当的神经元个数，训练次数等等，对于2018年10月11日与2018年10月12日两天的开盘价以及收盘价进行预测。本文中设置的输入层与输出层的神经元个数都为2，设置三层隐含层，通过修改三层隐含层个数来完成优化模型的预测。

利用BP神经网络进行预测时与实际的对比曲线如图8所示：

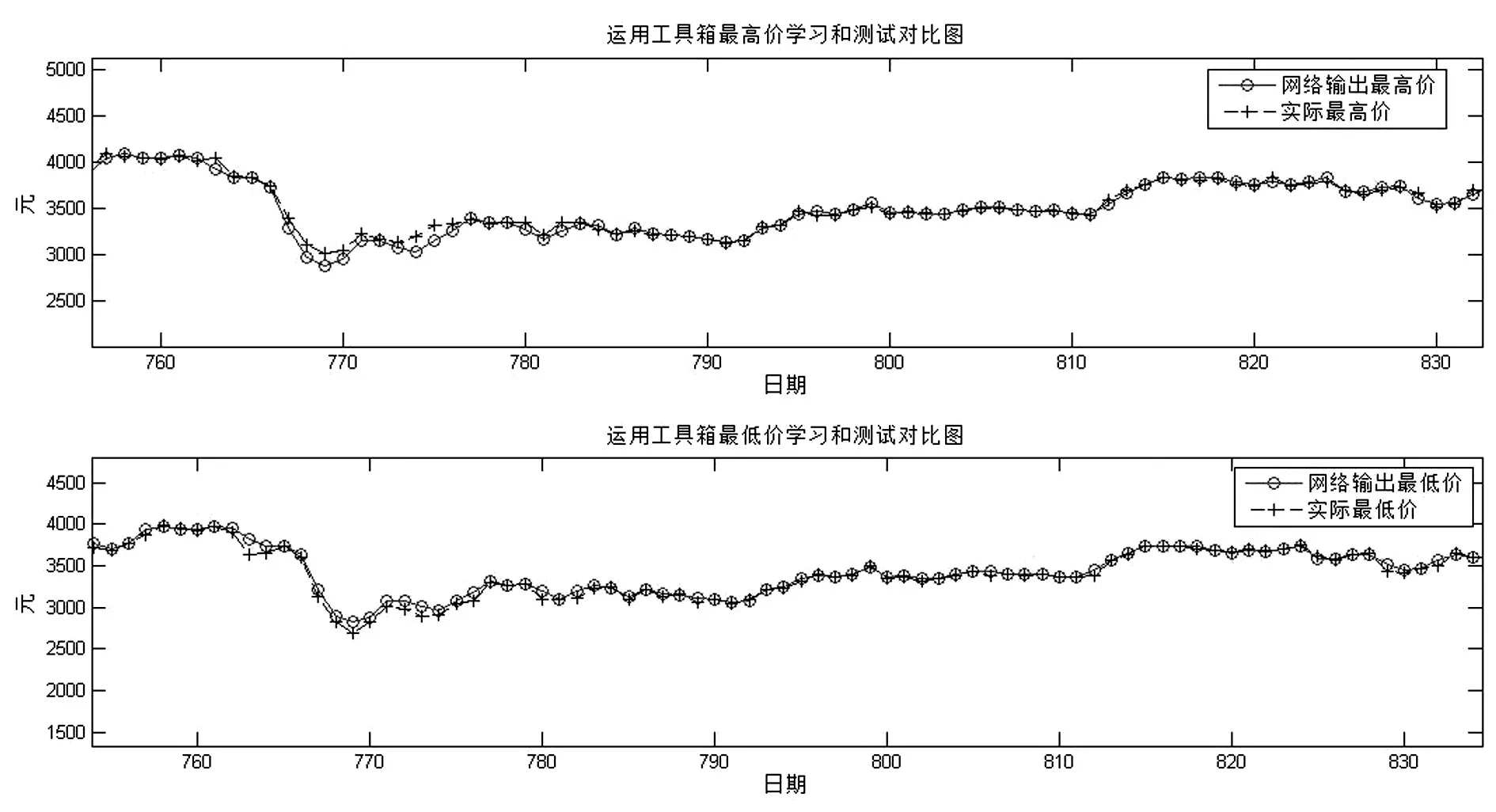
图8 BP预测最高价与最低价对比图

发现其预测效果并没有很好地达到预期数值，因此考虑将BP神经网络与小波去噪相结合，先对原始数据进行优化去噪，消除十分尖锐的异常数据再利用神经网络模型进行学习预测。

3 基于小波去噪的BP神经网络模型

先对数据进行四层小波分解试图消除数据中异常尖锐的点。再将优化处理后的数据与BP神经网络相结合进行学习。加入小波去噪后的数据拟合前后对比如图9所示：

图9 BP神经网络结合小波去噪拟合与实际对比图

收盘价，开盘价实际与预测值差异局部放大曲线如图10所示：

图10 局部放大图

通过修改各神经网络层神经元个数而得到的预测结果显示如表2所示：

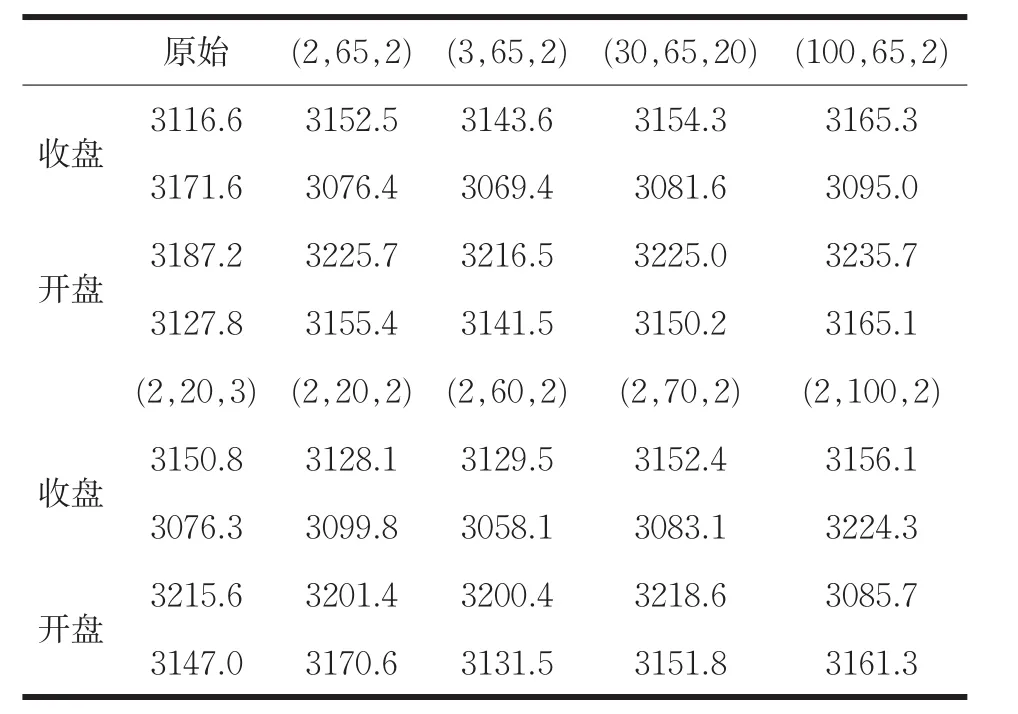
表2 模型通过修改神经网络参数得到的部分预测表

其中（J，K，L）：J：第一隐含层神经元个数；K：第二隐含层神经元个数；L：第三隐含层神经元个数，迭代次数为：5000。

通过不断调试参数本文得到三层隐含层神经元个数配比为（2，20，2）时，误差最小，经过计算得到误差约为1.1%，即准确率为98.9%，这说明了构建的模型有一定的参考价值，能进行推广。

4 结论

通过构建的两类不同的神经网络模型对沪深300股指期货数据进行分析预测从而寻找出了更为适宜的模型。分别将Elman神经网络模型与BP神经网络模型对数据进行分析，利用已有数据先使模型进行学习，再通过调试参数，反复修改神经元个数，以及学习次数等等优化途径不断减小误差，从而对不同模型的最终误差率进行比较。

由神经网络模型分析验证发现BP神经网络对于股指数据的预测误差率更低，因此首先考虑对BP神经网络进行优化处理，考虑利用小波去噪对于数据进行预处理，消除数据中异常尖锐的点，再将去噪处理后的数据代入模型中。经过不断调试误差率最终达到约为1.1%，但由于股指基数较大，此误差仍未能很好的达到预期，故仍需继续进行调试并将多种方法相互组合从而寻求最优的预测模型方案。