自升式平台压载作业桩腿侧向滑移的极限RPD
(中国船级社 海工技术中心, 天津 300457)
0 引 言
自升式平台是指具有活动桩腿,且其主船体能沿支撑于海底的桩腿升至海面以上预定高度进行作业的平台,此种平台在海洋石油开发中被广泛应用[1]。随着油气开采向深海发展,自升式平台的作业水深不断加大,其自身的结构安全问题越来越受到各方的重视。自升式平台在进行修井作业前,往往需要在已有的桩坑附近进行插桩,称为“踩脚印”,此过程极易产生桩腿侧滑,导致桩腿、升降系统以及平台结构损坏。2012年5月,“胜利作业3号”平台在渤海海域进行插桩作业时发生侧滑,平台结构严重受损,最终平台倾覆,发生严重作业事故;2017年6月,“HYSY944” 在中国东海海域进行修井作业时,艏部桩腿发生滑移,导致船首倾斜5°,3根斜撑、1根内水平撑发生变形。因此,对于自升式平台的“踩脚印”作业,应建立详细的预警方案和应对措施,避免滑移对平台结构造成损伤。
传统的齿条相位差(Rack Phase Difference, RPD)监测系统对桩腿各个弦杆变形进行监测,一旦桩腿变形接近临界值,RPD系统就会报警,船体升降操作必须停止,随后要按操作规程调整升降系统,使船体恢复水平。目前国外先进的自升式钻井平台都配备有RPD监测系统,比如:F&G公司JU-2000E平台的极限RPD为203 mm[2];Gusto MSC公司CJ46平台的极限RPD为58 mm[3]。BMC375平台上也安装了类似的监视系统,但其传统设计方法只是对桩腿强度进行极限RPD值分析,并没有涉及升降系统以及固桩区结构强度等,对于侧滑等特殊工况须综合考虑各种因素影响,因此并不适用。
本文对“踩脚印”过程的RPD计算原理进行研究,推算适用于桩腿侧滑的RPD计算方法;然后采用有限元分析方法模拟桩腿在不同方向、不同距离的侧滑,计算平台桩腿、升降系统以及固桩区结构强度,确定平台系统的临界极限能力;通过迭代搜索最终确定平台“踩脚印”时的极限RPD值。以某作业水深为400英尺(1英尺=0.304 8 m)的自升式平台为例,通过上述原理和方法计算桩腿滑移过程的极限RPD值,并以此得出几个有益的结论。将RPD理论应用于自升式平台“踩脚印”插桩过程,当桩腿变形接近临界值时,RPD监测系统报警,提醒作业者及时调整平台插桩状态,可有效降低桩腿的侧滑风险,对设计者和作业者具有较强的指导作用,应用价值较高。
1 RPD计算原理
RPD的定义为桁架式桩腿的两相邻弦杆具有相同标高的齿条板相对于升降室顶部的垂向位移的绝对差值。测量时需记录不同主弦杆上具有相同标高的齿节点距离参考平面的垂直距离,即齿条相位值(Rack Phase Value, RPV),再经计算得到桩腿上的RPD值[4]:
RPD=max(|RPVi-RPVj|)
(1)
式中:i、j为任意两根相邻弦杆。
在常规情况下,平台的极限RPD值表征桩腿可容许的最大弯矩,与桩腿支撑杆的轴向屈曲密切相关。其理论计算方法一般为:建立桩腿的有限元模型,模拟升降系统、上下导向结构作为边界条件,在桩腿底部位置加载垂向载荷;下导向位置施加弯矩,此弯矩值应使桩腿弦杆或撑杆发生屈曲(应力比接近1.0),此时可计算分析得到3个弦杆的垂向位移,即可计算得到极限RPD值[5]:

(2)
式中:ΔZmax为计算得到的弦杆垂向位移差值;UCL为桩腿构件的最大名义应力与许用应力的比值;ΔZ0为桩腿初始倾斜产生的垂向位移差值。
在一般情况下,桩腿弦杆齿条板与上下导向之间会存在一定的间隙,尤其对于老龄平台,当齿条板和导向板存在磨损时,这一间隙不可忽略。间隙的存在使桩腿相对于主船体存在一定的初始倾斜而不会产生桩腿应力,这部分倾斜所导致的RPD称为无限制RPD。
当自升式平台在旧脚印附近就位时,极易引起桩腿滑移,不但对桩腿结构构成危害,还对导向产生挤压,甚至使升降系统过载。因此,自升式平台“踩脚印”过程极限RPD的计算原理应综合考虑桩腿结构、船体结构及升降系统极限能力等3个方面的因素,进而推算出适用于桩腿侧向滑移的极限RPD值:

(3)
UCmax=max(UCL,UCH,UCJ)
(4)
式中:UCH为船体构件(包括围肼区及固桩架结构)的最大名义应力与许用应力比;UCJ为升降系统最大受载与升降能力比。UCmax取三者中的最大值。
2 “踩脚印”时的平台极限能力
自升式平台极限滑移能力指的是平台结构所能承受的最大侧向滑移距离,超过该滑移距离,则平台桩腿、升降装置或平台桩腿下导向结构就会发生损坏。
2.1 计算模型
为计算出“踩脚印”时的平台极限能力,一般需要建立有限元模型,保证模型刚度、质量及载荷模拟与实际预压载条件一致。
(1) 桩腿刚度。桁架式桩腿弦杆一般采用相当刚度的梁进行模拟,梁的刚度应与实际桩腿一致。确定刚度的主要要素包括截面面积、截面惯性矩、剪切面积和扭转惯性矩。桩腿撑杆则按照实际结构以管单元模拟。
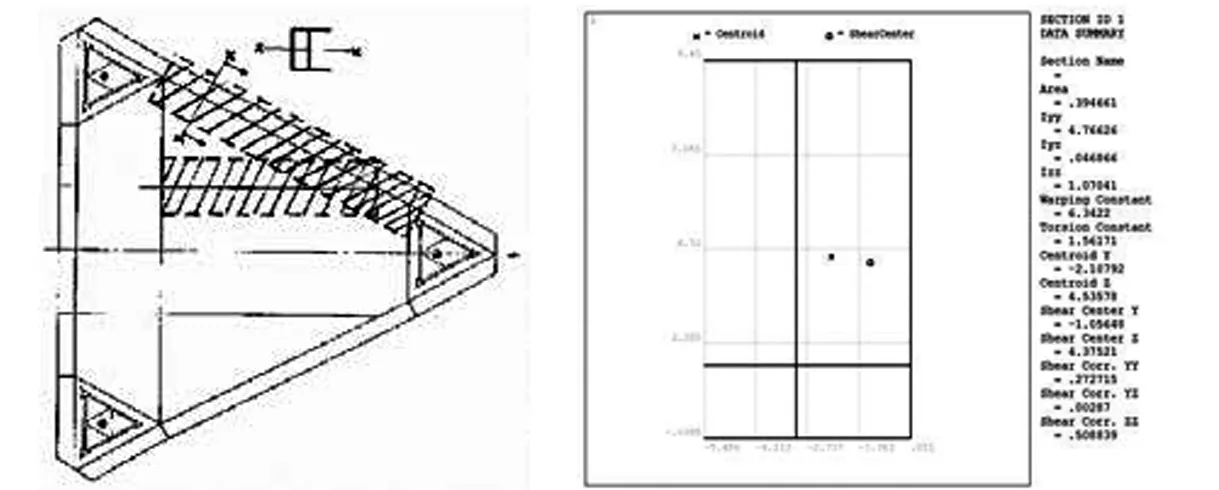
图1 平台主船体舷侧舱壁等截面梁模拟方法
(2) 主船体刚度。根据研究对象的不同,平台主船体的刚度一般有简化模拟和详细模拟两种方法。
在分析桩腿强度时可应用简化方法,即采用等截面梁单元模拟平台主船体,将平台实际的横纵舱壁及各层甲板简化为梁架结构,同时保证截面惯性矩、剪切面积及扭转惯性矩与平台结构一致,具体的等效方法可参见SNAME 5-5A[6]。平台主船体舷侧舱壁等截面梁模拟方法如图1所示。
在分析固桩区及船体结构时,需应用详细模拟方法,即采用板、梁单元完全模拟平台横纵舱壁、各层甲板及固桩区结构,单元尺寸及属性与平台实际结构一致。
(3) 桩腿-升降系统连接。为准确模拟桩腿侧向滑移对升降系统及上下导向的载荷传递,应充分考虑桩腿和船体的连接刚度。在有限元分析中,建立详细的固桩架模型,并在导向及升降齿轮的位置与桩腿之间采用弹簧单元模拟。单个弦杆上升降系统弹簧垂直刚度系数KV,j可用式(5)[7]表示:

(5)
式中:np为单弦杆上的齿轮个数;KV,p为单个齿轮的垂向刚度系数;KV,jh为单弦杆升降齿轮箱的垂向刚度系数。
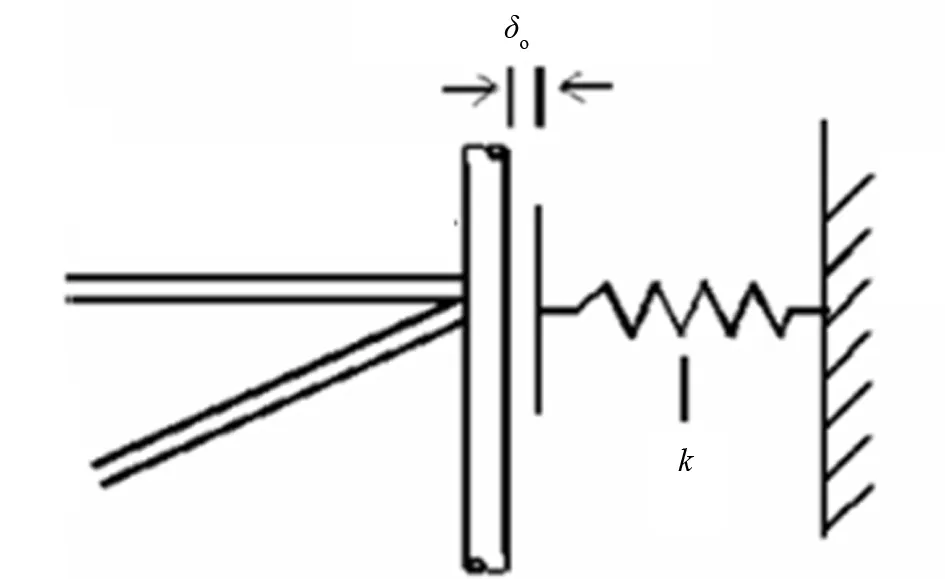
图2 桩腿与导向之间的非线性弹簧单元示例
(4) 桩腿-导向连接。为准确模拟桩腿与导向之间间隙导致的无限制RPD,在有限元分析时,可在上下导向与桩腿之间采用非线性弹簧单元连接,单元设置初始间隙δ0,且单元仅在接触后轴向受压,如图2所示。
(5) 边界条件。在平台预压载过程中,由于土壤处在不断被桩靴压实的过程,因此无法确定准确的土壤刚度。如果考虑水平方向的土壤刚度,可使桩靴允许的滑移距离增大;而考虑土壤的转动刚度,则使桩靴允许的滑移距离减小。通过敏感性分析发现,将桩端简化为铰支约束(水平刚度无限大,转动刚度为0),与同时考虑水平刚度和转动刚度的计算结果差别不大。因此,对于不滑移桩腿,可采用铰支约束,滑移桩腿则通过给定强制位移模拟侧向滑移。
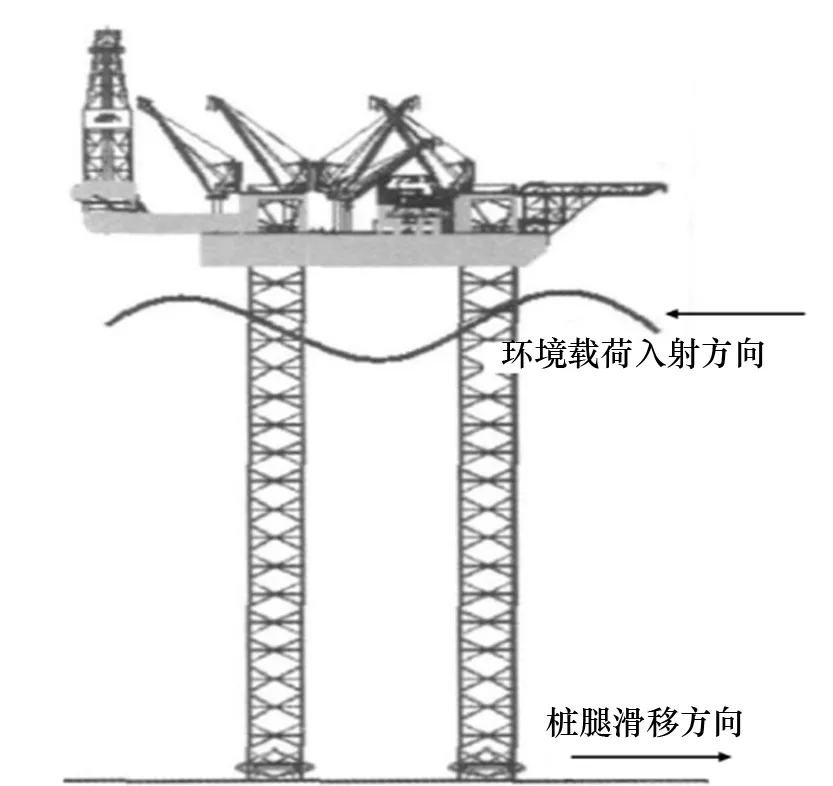
图3 桩腿滑移方向与环境载荷入射方向关系
2.2 桩腿侧滑计算载荷
将平台整体结构作为研究对象,计算预压载时桩腿侧向滑移需考虑的载荷包括重量载荷、环境载荷及桩端侧向位移。
(1) 重量载荷包括固定载荷、可变载荷及压载水重量。
(2) 环境载荷为平台压载作业时受到的载荷,包括风载荷、波浪载荷、海流载荷及P-Δ效应载荷等,具体计算方法参见CCS相关规范[8]。
(3) 桩端侧向位移是模拟平台某一桩腿发生侧向滑移产生的大变形对平台及桩腿造成的不利影响。
关于载荷方向需强调的是,由于实际就位点与旧脚印之间方位的不同,需研究不同滑移方向对结构的影响,因此在0°~180°范围内进行多方向滑移分析。出于保守考虑,环境载荷的入射方向按照加重结构破坏的原则,向桩端滑移的反方向施加,如图3所示。
2.3 平台极限能力
为保证平台结构安全,平台踩脚印时的极限能力应确保桩腿结构、船体、固桩架结构以及升降系统均不发生损坏,即
UCmax=max(UCL,UCH,UCJ)≤1
(6)
式中,桩腿及船体的极限强度UCL、UCH可通过有限元模型分析得到,平台升降系统的最大承载能力可由升降系统生产厂家提供,UCJ可利用整体分析模型中提取弦杆上的垂向力与单个弦杆上所有齿轮的最大能力进行比较得到。通过不断加大平台的侧向滑移距离,直至某一指标接近1.0时,该侧滑距离即为平台极限滑移距离。
3 算例分析
3.1 算例计算模型
算例平台为某作业水深为400英尺的自升式钻井平台,采用三角箱形主船体,配有3个桁架式桩腿(艏1艉2),升降系统为电动齿轮升降系统,每个桩腿有4套弦杆,每个桩腿底部带有1个圆形的桩靴。为分别考察桩腿强度和固桩区局部强度,建立算例平台简化模型及详细模型,如图4和图5所示。
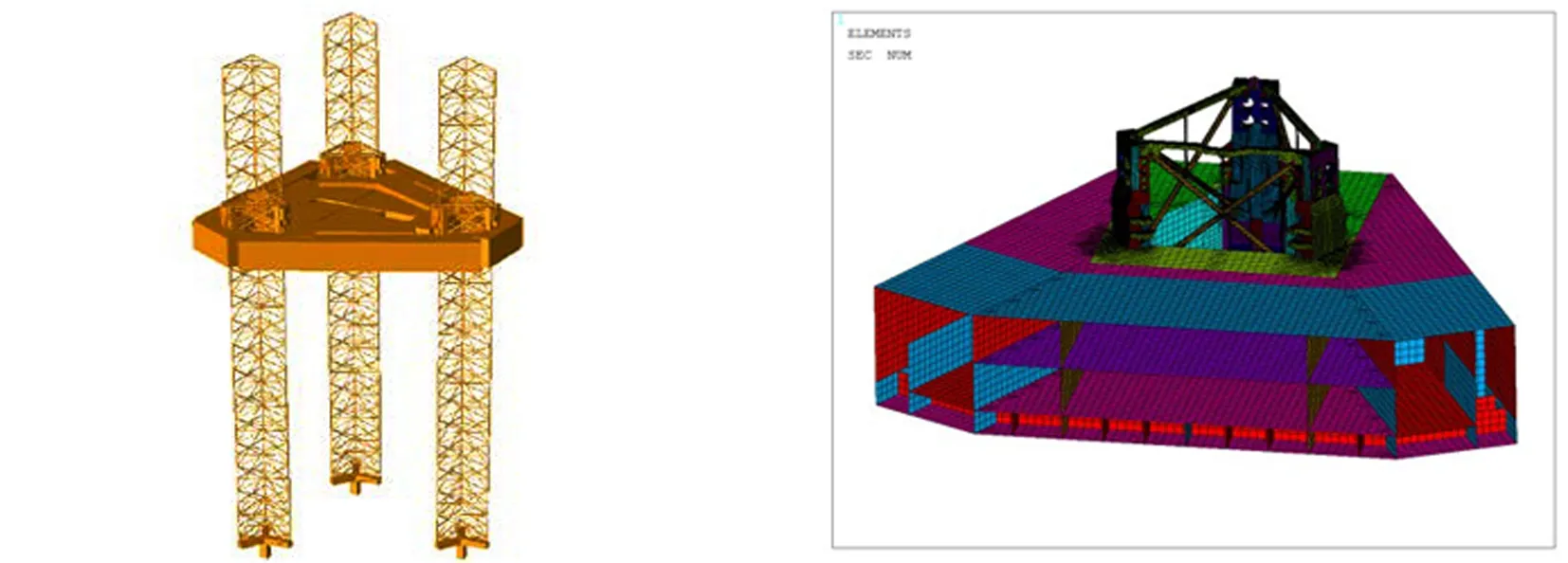
图4 算例平台简化模型 图5 算例平台详细模型
3.2 算例计算载荷
算例平台的环境条件等主要参数如表1所示。

表1 预压工况下平台的环境条件及主要参数
3.3 计算结果分析
假定平台桩靴在不同方向上产生侧向滑移,通过不断增大滑移距离反复计算,直到UCmax接近1.0为止。图6为艏桩腿滑移距离与UCmax关系图,图7为右舷桩腿滑移距离与UCmax关系图。
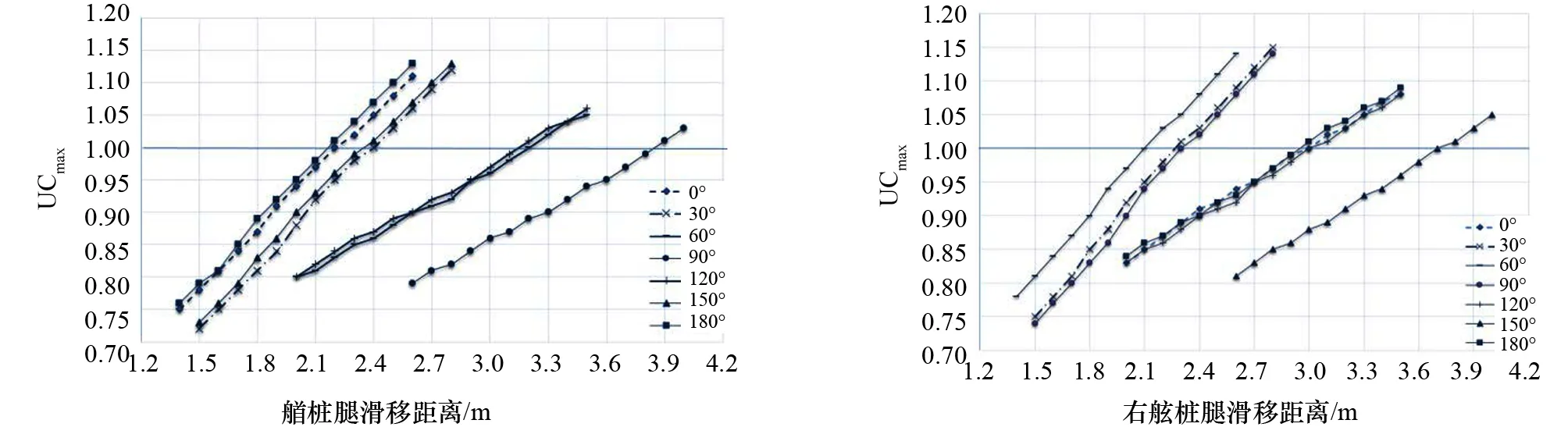
图6 艏桩腿滑移距离与UCmax关系图 图7 右舷桩腿滑移距离与UCmax关系图
计算结果显示,当平台单桩达到最大压载量时,在被压桩腿发生侧向滑移过程中,升降系统先过载,继续增大侧滑距离,桩腿撑杆发生屈曲,平台围肼区下导向附近结构随之发生屈服。以艏桩腿为例,升降系统、桩腿结构和船体结构的UC值如表2所示。

表2 艏桩腿滑移UC值
对于艏桩腿,当桩靴向0°方向滑移时,可允许的滑移距离最小,90°方向可允许的滑移距离最大;相应地,右舷桩腿60°方向可允许的滑移距离最小,150°方向允许的滑移距离最大。图8~图10为艏桩腿向0°、90°及右舷桩腿向60°方向滑移的桩腿变形图。

图8 艏桩腿0°方向滑移 图9 艏桩腿90°方向滑移 图10 右舷桩腿60°方向滑移

图11 艏桩腿90°方向滑移3.8 m围肼区结构应力云图
以艏桩腿为例,算例平台艏桩沿着90°方向滑移至最大3.8 m时,船体结构强度UCH达到0.96,最大UC值出现在滑移桩腿下导向处。此时平台围肼区下导向结构应力云图如图11所示。
研究表明,算例平台在不同方向上可允许的最大滑移距离不同,图12和图13为艏桩腿、右舷桩腿的最大滑移距离平面包络图,可为平台指定“踩脚印”方案提供理论指导。
算例平台桩腿滑移距离与RPD关系如图14所示。由于算例平台为三角形桁架式桩腿,根据桩腿与固桩架的轴对称性,将0°~60°作为研究对象, 其他角度可根据对称性求得。基于保守考虑,取桩腿滑移各个方向上的最小RPD值作为RPD监测系统的报警值。根据以上计算结果可查出算例平台在预压载侧滑工况下的极限RPD值,艏桩腿为127 mm、艉桩腿为125 mm。

图12 艏桩腿最大滑移距离包络图 图13 右舷桩腿最大滑移距离包络图

图14 桩腿滑移距离与RPD关系图
3.4 结论和建议
(1) 艏部桩腿的极限侧滑距离略大于艉部桩腿侧滑距离,这与平台首尾结构形式和桩腿间距不同有关。
(2) 对于给定的某一桩腿侧滑,不同方向上产生的最大或最小极限侧滑距离必然产生最大或最小的RPD值,符合侧滑距离越大,对结构产生不利影响越大、结构变形越大的趋势。
(3) 艏桩腿最大侧滑距离和最大RPD出现在90°或270°侧滑方向,最小侧滑距离和最小RPD出现在0°或180°侧滑方向;艉桩腿最大侧滑距离和最大RPD出现在150°或330°侧滑方向,最小侧滑距离和最小RPD出现在60°或240°侧滑方向。
(4) 从侧滑破坏的形式上分析,一般趋势是升降齿轮首先超载,然后桩腿结构发生破坏,最终下导向及围阱区结构损坏。此趋势与平台设计理念有关,也基本符合实际侧滑结构损伤情况。
(5) 在实际压载作业时,平台上很难判断具体的侧滑距离,因此应通过RPD监测系统报警值确定平台结构安全程度。在实际插桩时也很难判断具体的滑移方向,基于保守考虑,取桩腿滑移各个方向上的最小RPD值作为RPD监测系统的报警值。因此,算例平台的桩腿可容许极限RPD值为艏桩腿127 mm、艉桩腿125 mm。
4 结 语
“踩脚印”过程发生桩腿侧滑是自升式平台插桩时遇到的重要作业风险,作业前应建立起详细的预警方案和应对措施,降低滑移对平台带来的结构损伤风险。对自升式平台“踩脚印”过程的RPD计算原理进行研究,提出了适用于桩腿侧滑的RPD计算方法,对自升式平台减少“踩脚印”侧滑风险危害具有一定的指导意义。但是,由于海底条件的复杂性以及实际作业的不确定性,该理论分析方法仍需在进一步的实际工程验证中不断完善。

