随机裂隙网络储层与井筒热流耦合数值模拟

单丹丹 闫 铁 李 玮 孙士慧 逯广东 赵 欢

1.东北石油大学石油工程学院 2.提高油气采收率教育部重点实验室·东北石油大学

0 引言

干热岩是一种深层热岩体，其资源储量极其丰富[1-2]。增强型地热系统（Enhanced Geothermal System，EGS）是目前开采干热岩资源最有效的技术手段[3-4]。EGS的设计与优化主要依据两方面重要因素——出力与寿命[5]。对系统出力与寿命进行评价，要反复模拟EGS热流耦合过程。针对这一耦合过程，建立相应的数学模型，并进行井筒—随机裂隙网络储层耦合数值模拟，可以预测EGS运行状态、利用效率与使用寿命，对系统进行采热评价[6]。对于热储内裂隙岩体热流耦合的数学模型可分为等效连续介质模型与离散裂隙网络模型两大类[7]，后者不仅与现实更接近，且能更好地模拟水热迁移过程，因而受到广泛的关注[8-14]。显式模拟裂隙的离散裂隙网络模型虽接近于真实情况但计算量较大[15]。由于裂隙宽度方向相对于其他两个方向，其尺度小到可以忽略，Juanes等[16]提出在描述裂隙的过程中可以采用低一维的单元来进行。在裂隙网络生成上，大部分研究都依蒙特卡罗方法随机生成[17]。关于随机裂隙网络储层的热流耦合研究很少考虑到井筒部分的热损失，而在对井筒—热储耦合模拟的研究中，大多是将储层看作是单孔隙等效多孔介质模型。Jiang等[18]建立了井筒与热储循环通道热流耦合瞬态模型，其中储层被视为单一孔隙度的等效多孔介质。Zeng等[19]提取了DP23-1井的地质资料，研究了干热岩储层的热潜能，其储层也被看作是等效多孔介质。曹文炅等[20]在局部非热平衡假设的基础上，用理想的垂直井模型模拟了EGS的采热能力，热储部分同样以多孔介质来代替，忽略了裂隙的存在。长深井筒的热损失及随机裂隙网络储层的热流耦合过程在循环系统的整体采热评价中都占据着主导作用，为此有必要开展二者的热流耦合模拟。由于COMSOL软件在多物理场耦合与裂隙细微结构、井筒细长结构的多尺度耦合上具有强大优势，故选用其进行二维有限元数值模拟，可形象展现系统渗流传热过程，在此基础上分析热物性参数与几何参数变化对裂隙面温度、采出温度、热开采速率等的影响，得出影响系统产能与寿命的各项因素，以期为相关领域设计与施工提供理论依据。

1 井筒—随机裂隙网络储层热流耦合数学模型

1.1 基本假定

人工热储可以简化为由基质岩块和裂隙组成的双重介质模型，基质岩块视为孔隙介质，相比于裂隙，其渗透率极低，而人工压裂形成的裂隙网络才是热储层中主要的渗流通道[21]。由于高压作用，液态水不可能发生气化，导致系统内的流动为单相水流。井筒、开孔与裂隙网络构成水循环的主要通道，在注入井与采出井井口压力不变的条件下，这一通道内的流体流动相对于几十年的系统运行时间而言，很快会达到流速稳定，因此在EGS模拟中，流动过程是稳态的而传热过程是瞬态的，这种近似对于系统的长期运行而言是合理的。对于稳定的渗流系统，井筒、开孔及裂隙网络中流体的流速应相同，均服从达西定律[22]。岩体的热量主要通过对流换热及热传导的形式向外传递。不考虑岩体及裂隙网络的体积变化，认为系统整体不存在力学场，仅对井筒与热储耦合的渗流场和温度场进行模拟。

1.2 数学模型

水在EGS中的流动可分为4个性质不同的子区域：①具有井筒壁的细长流道—注入井井筒、采出井井筒，其与基岩之间只有热量传递，无质量传递；②无井筒壁的开孔位置，视为多孔介质，与热储裂隙及基岩既有传热过程，也有传质过程；③服从达西定律的人工热储内裂隙网络；④极低渗透性基质岩块（包括除井筒、开孔、裂隙网络外的一切地层岩石）。模型基于前述假定条件，流动为单相水流，既不考虑循环水与岩石的化学作用及水的物性变化，也不考虑岩石热应变引起的裂隙网络孔隙率及渗透率的变化。在以上假设基础上，分别得出井筒与基岩之间的热传导模型、裂隙网络内渗流模型、裂隙网络中的传热模型及开孔、基岩渗流与传热模型。

井筒与基岩单位长度的径向热传导为：

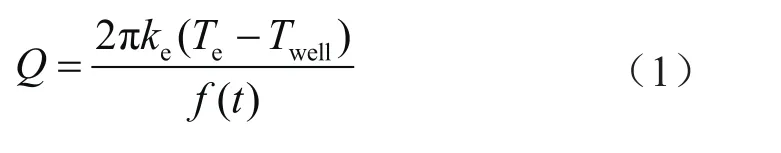
式中α表示地层热扩散系数，m2/s；t表示加热（或冷却）时间，h；r表示井筒半径，m。

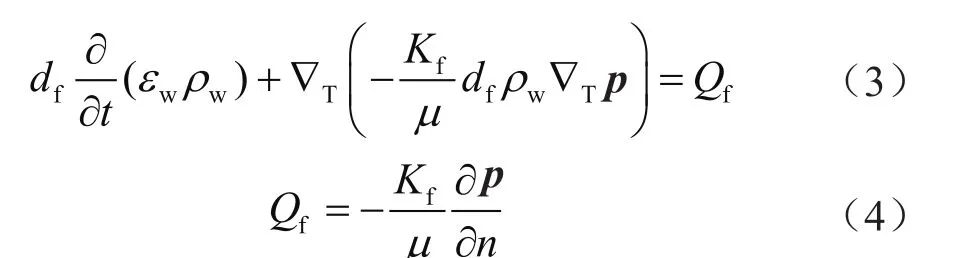
裂隙网络内渗流平衡方程为：式中df表示裂隙宽度，m；εw表示裂隙的孔隙率，无量纲；ρw表示水的密度，kg/m3；Kf表示裂隙内的渗透率，m2；μ表示水的动力黏度，Pa·s；Qf表示基岩与裂隙面的流量交换；n表示裂隙面法向；表示沿裂隙α切向求导；p表示压强场，为一矢量。

裂隙网络温度场方程为：

其中

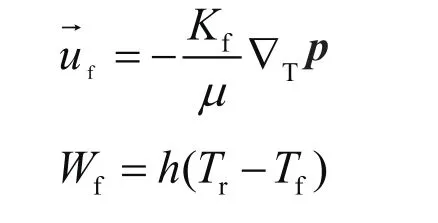
式中cw表示水的比热容，J/(kg·K)；Tf表示裂隙内水的温度，K；λf表示水的热传导系数，W/(m·K)；Wf表示裂隙表面水从基岩吸收的热量，W/m2；h表示裂隙水与基岩边界处的对流换热系数，W/(m2·K)。

开孔、基岩渗流场方程为：

创客是坚守创新、坚持实践、乐于分享并且追求美好生活的一群人，是把兴趣与爱好努力变成现实的人，是社会迎来新一轮的“科技社会化”浪潮，是一场快速由工业社会向信息社会过渡的运动。创客空间的普及发展，使分布式、数字化、个性化、定制化的电脑网络制造方式取代传统的工厂加工制作方式。作为未来人才培养基地的学校应该培养更多的创客，打造“创客校园”。

其中

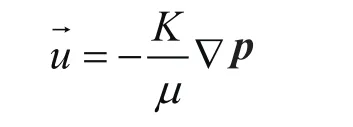
式中ε表示开孔、基岩的孔隙率，无量纲；K表示开孔、基岩的渗透率，m2；Qm表示渗流的源汇项。

开孔、基岩温度场控制方程为：

式中ceff表示开孔、基岩的等效比热容，J/(kg·K)；λeff表示开孔、基岩的等效热传导系数，W/(m·K)；Tr表示开孔、基岩的温度，K。

2 数值模型与边界条件

2.1 概念模型

EGS循环系统包括注入井、人工热储、采出井以及基质岩块4个部分，所建立的概念模型见图1。

2.2 二维裂隙网络的生成

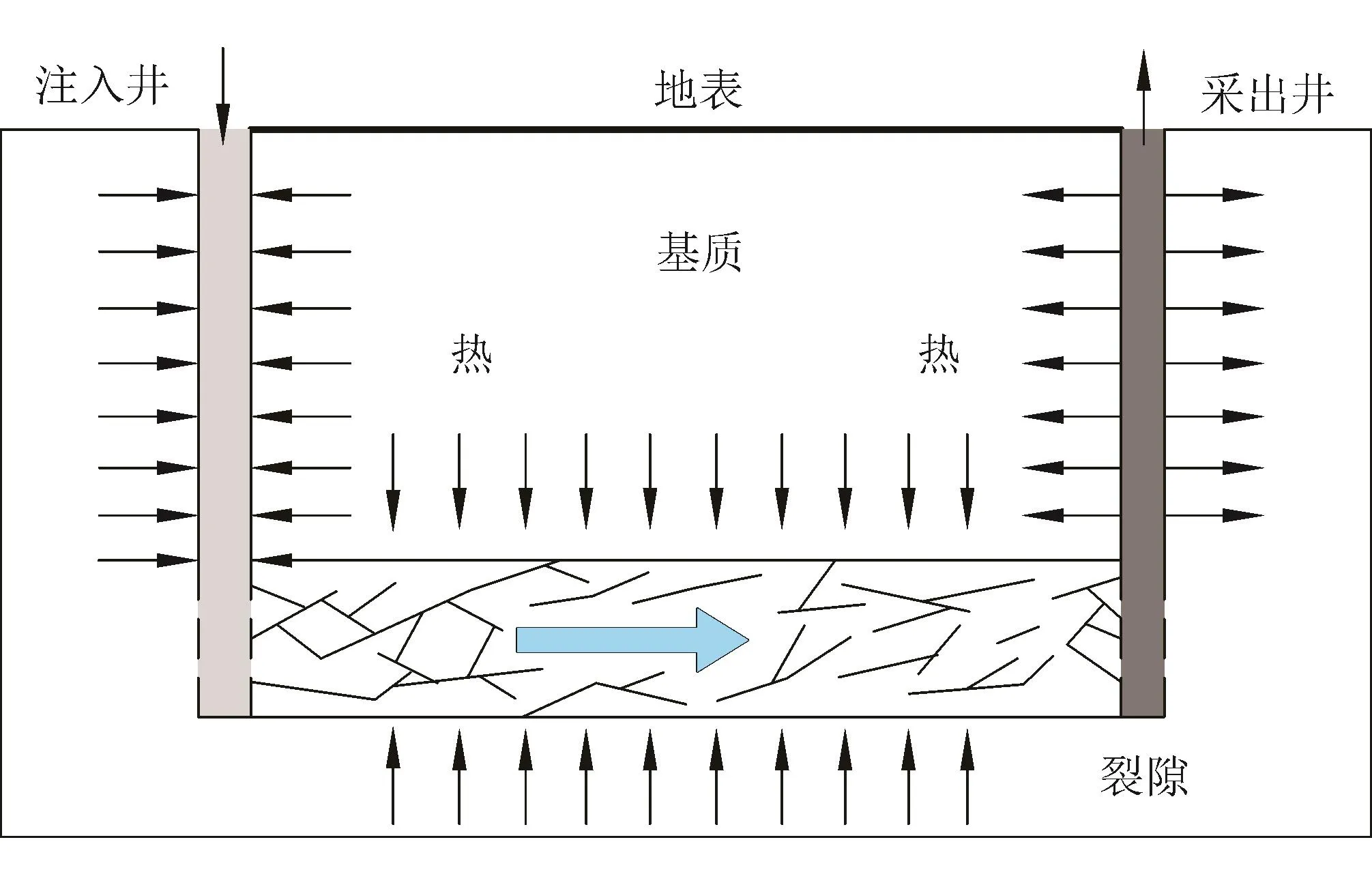
图1 EGS概念模型图[23]

Dershowitz和Einstein[24]总结了几种岩石节理体系且提出对其描述所需的参数。复杂的三维裂隙网络不但会使运算速度缓慢，且其依据参数随机生成，和二维计算结果相差并不很大，因此采用二维随机生成的裂隙网络系统进行模拟，所要用到的参数有裂隙的密度、迹长、开度及产状。在裂隙的生成上以Monte-Carlo方法为基础，拟定两组方向裂隙，分别与水平方向呈30°和150°，且具明显的各向异性。裂隙网络中各条裂隙的迹长服从正态分布，其长度平均值为60 m，方差为20 m，裂隙的数目为800个，裂隙的范围是 500 m×500 m。

2.3 有限元模型

借助数学软件MATLAB进行代码编写并运行得出裂隙网络模型，之后将生成的脚本文件导入到AutoCAD中形成图形文件，去掉伸出裂隙边界的孤立段，再进行井筒及周围基岩的绘制，完成建模过程，最终导入到COMSOL软件中进行模拟计算。依据上述方法建立的有限元模型如图2所示。

图2 有限元模型图

有限元模型中，假定采用以下的初始条件及边界条件。其中热物性参数数据参见表1。模型的渗流场、温度场及井筒壁（保温层）边界条件如下：

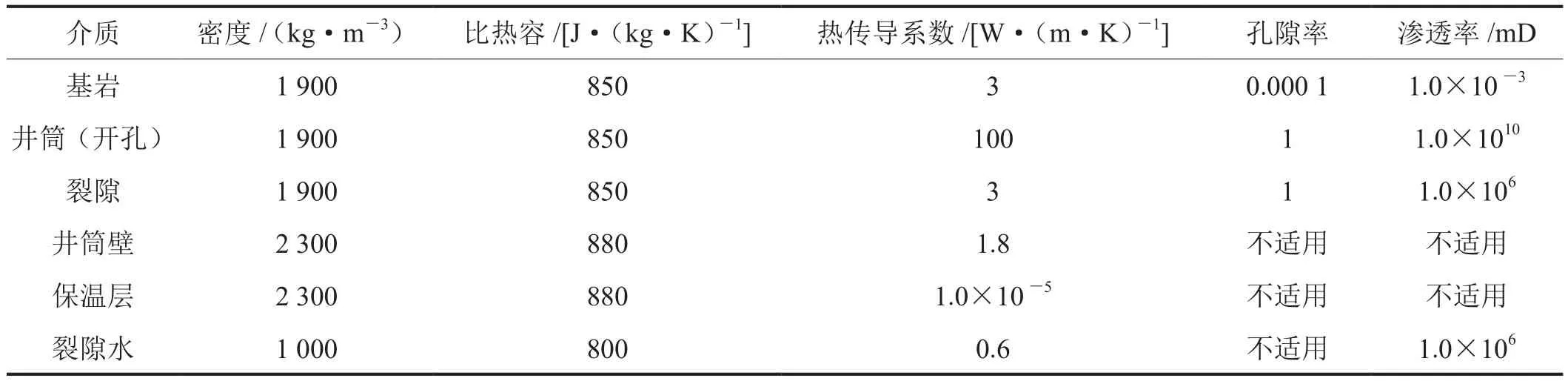
表1 热物性参数表

1）渗流场边界条件：注入井井口压力，16 MPa；采出井井口压力，10 MPa；热储外的花岗岩渗透率非常低，故取不透水边界，即q=0。

2）温度场边界条件：注入井井口温度为20 ℃，地温梯度为50 ℃/km，热流边界条件为井筒壁（保温层）与周围地层的传热过程用多孔介质传热模块里的薄层来设置，厚度取0.01 m。

3）井筒壁（保温层）边界条件：在注、采井井筒左右两边添加线段，代表两井的井筒壁及保温层边界，1、2、3、4代表注入井井筒左右两边的井筒壁及保温层边界，5、6、7、8则代表采出井井筒左右两边的井筒壁及保温层边界（图3）。

3 模拟结果与分析

基于假定的热物性参数与几何参数，研究这些参数变化对采出温度与热开采速率的影响。拟定的几组算例如表2所示。

3.1 对算例1进行模拟与分析

图3 井筒壁（保温层）示意图

以算例1为参考条件，在给定的已知参数条件下对其进行数值模拟，得出系统运行5年、10年、15年、20年的温度分布云图（图4）。可以看出，运行初期注入井周围地层由于热传导作用而降温的范围较小，即影响半径较小，随着运行时间的增长，被井筒内水流改变的地层温度场范围逐渐增大。裂隙储层内的温度场分布也有类似的性质，即时间越长，井筒周围地层及热储内基岩被冷却的范围越大。这是由于水流流经系统时带走了地层中的热量，然而水循环没有停止，而裂隙储层的温度却越来越低，导致流入采出井的热水温度也越来越低，从而使开采温度逐年降低。

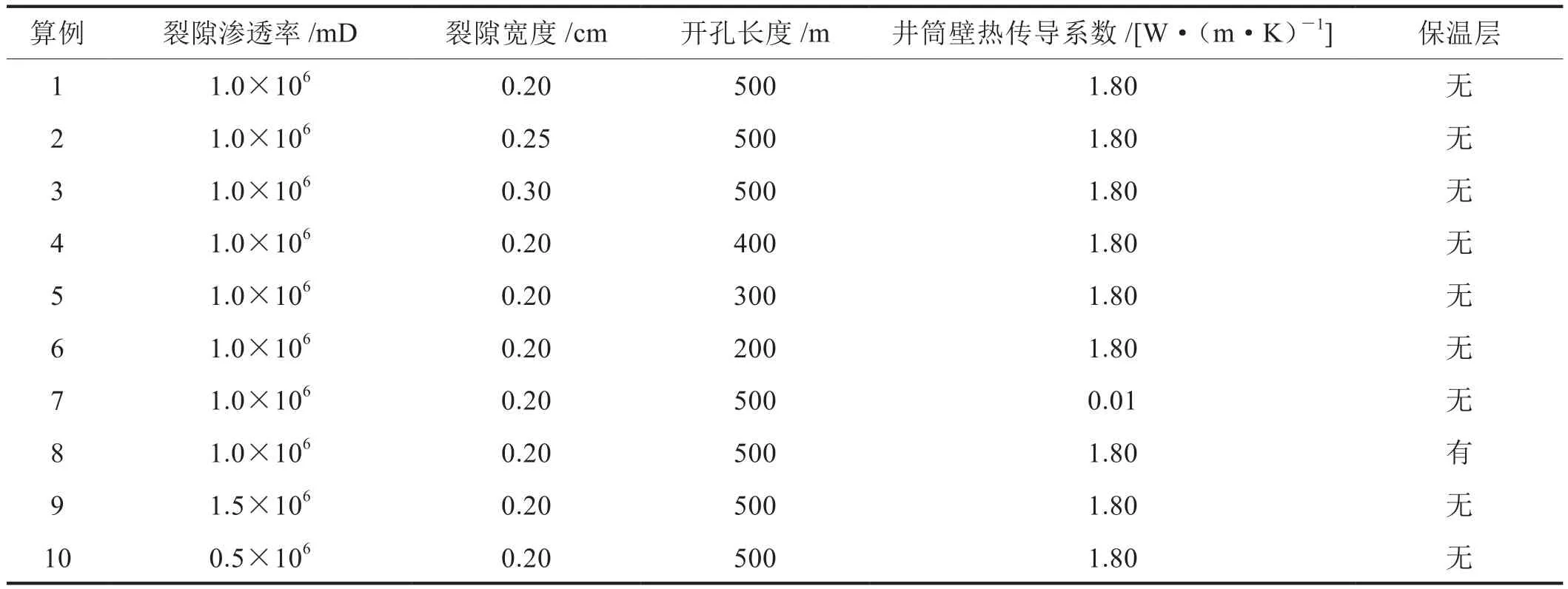
表2 数值模拟算例表

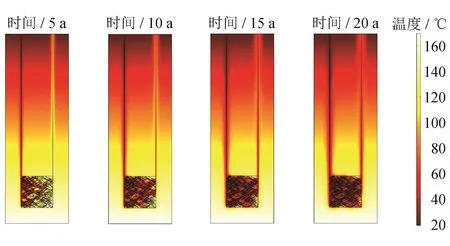
图4 温度分布云图

3.2 裂隙面与采出井温度

在裂隙面上选取1～5号点（图5-a），分析其温度随时间的变化规律（图6-a）：裂隙面上各点温度都随时间推移而降低，且越靠近注入井温度越低，越靠近采出井温度越高。这是由于注入井井筒内水温较低而采出井附近基岩温度较高，注入井内的低温水就近改变周围裂隙储层，高温的基岩就近改变附近裂隙水所致。在采出井井筒内选取A～E共5个点（图5-b），分析其温度随时间的变化规律，得到如图6-b所示的变化曲线。可以得出：温度总体上都随时间的增加先升高而后降低，这是由于基岩温度较裂隙水高，在其发生热交换时，水流温度升高而基岩温度降低，随着时间的增加，基岩降低的温度来不及补给从而导致水流温度下降，采出井内水温降低。

图5 裂隙面及井筒取点位置简图

3.3 井筒壁与保温层

图7 为算例1、4、5、6的采出井采出温度变化曲线。由图可知，热突破时间随开孔长度（L0）增大而提前，且相应的冷尾迹效应也更明显。若以采出井采出温度相对最高采出温度下降20%作为系统运行寿命的指标，则L0=300 m、400 m、500 m时的最高采出温度分别为114.00 ℃（第5年），116.98 ℃（第4年）与117.81 ℃（第3年），系统的寿命分别为12年、10年、8年。三者之中L0=300 m时系统寿命最长，但最高采出温度较L0=400 m时低了2.98 ℃，且晚了1年时间。综合出力与寿命两项因素，选取L0=400 m作为最佳开孔长度，不仅可以得到较高的开采速率，还能保持一定的系统寿命。

图6 各点温度随时间变化曲线图

图7 开孔长度影响采出温度曲线图

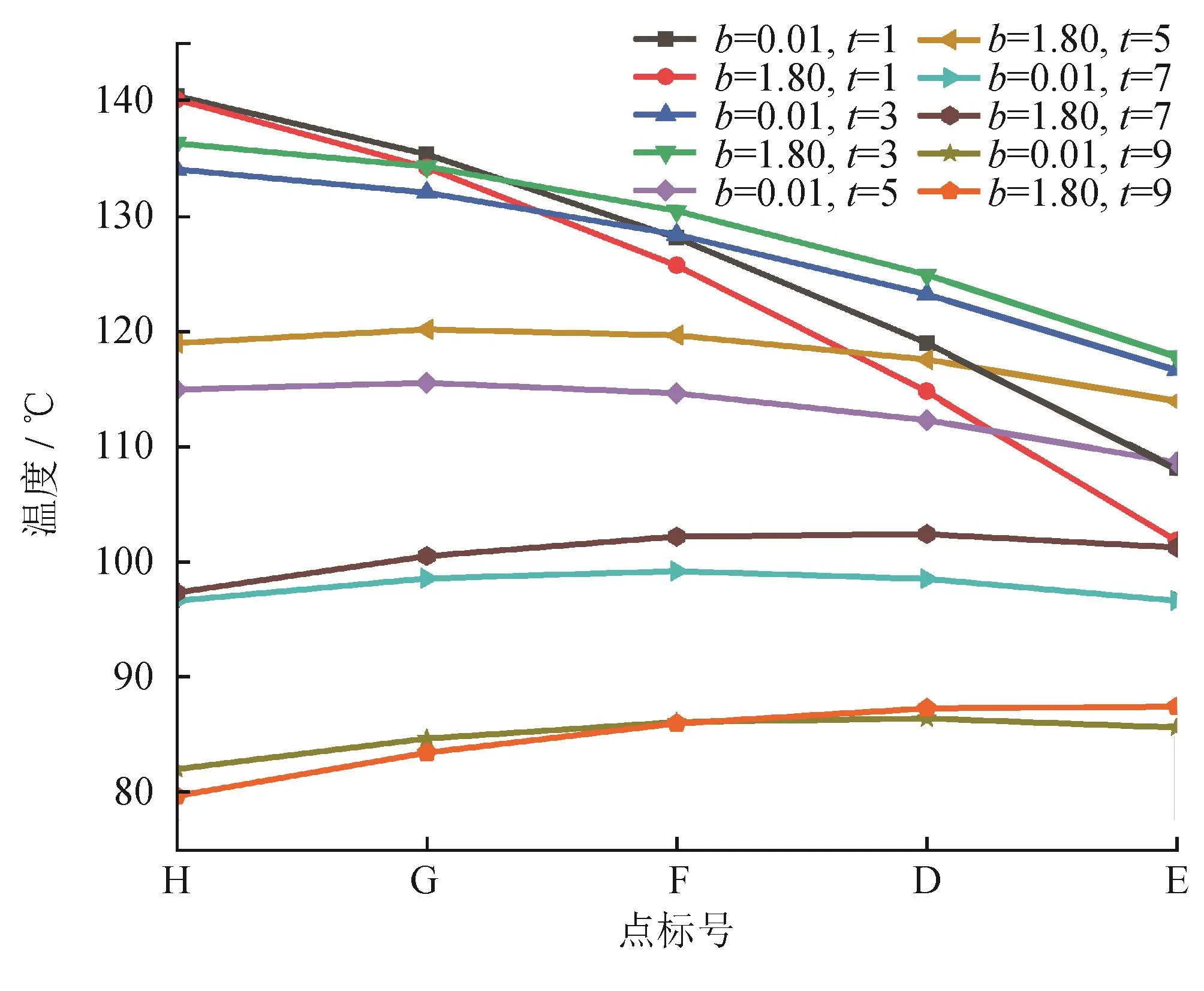
图8 井筒壁热传导系数影响温度曲线图

图8给出了算例1、7的采出井井筒内温度变化曲线。横坐标代表标号为D～H各点，这5点坐标分别为 H（500.1 m，950 m）、G（500.1 m，1 400 m）、F（500.1 m，1 850 m）、D（500.1 m，2 300 m）、E（500.1 m，2 750 m）。可以看出，开采初期（1年），温度沿井筒向上逐渐降低，且随热传导系数增大而降低得更快，这是由于热传导系数增大促进了与基岩的换热过程。开采前、中期（3、5、7年），温度沿井筒向上降低的速度减缓，甚至中期不降反升，其原因在于储层温度不断降低，导致井内流体温度降低，井内流体从周围基岩吸热使得温度升高，热传导系数越大越有利于热量吸收，从而温度升高更快。进入开采后期（9年），基岩被井内流体冷却得较彻底，致使二者温度相差不大，这时井内流体温度与井筒壁热传导系数关系不大。

图9给出了算例1、8的温度变化曲线。有保温层的井筒壁与地层之间的换热受阻，会使得采出温度很快升高到最大值，即热突破时间提前，但温度却很快下降，这与减小井筒壁热传导系数的情况一样。说明保温层能提高初、前期的采出温度，进而提高这期间的开采速率。

图9 保温层影响产出温度曲线图

3.4 采出温度及热开采速率

图10 、11为裂隙渗透率及裂隙宽度影响采出温度与热开采速率的变化曲线图。当裂隙渗透率（Kf）增大至 1.5×106mD，裂隙宽度（df）增加至 0.30 cm时，最高采出温度均超过120 ℃，且二者对采出温度及热开采速率的影响表现出相同的规律性，即随参数值的增大而产生较早热突破，冷尾迹也更明显，最高采出温度和最大热开采速率也都有所提高。原因在于二者的物理效应是等同的，裂隙宽度增加会导致渗透率增大，从而使冷却时间提前，热开采速率提高，缩短开采寿命。实际工程中，裂隙宽度会不断变大，这是由于循环水会对裂隙产生挤压变形，使流过区域宽度增加，进而扩大换热面积，降低了开采年限。为保持长时间的热能开采，要想改善这种状况，应停止开采一段时间，待储层温度恢复后再次提取地热能。

4 结论

1）考虑井筒流动换热的井筒—热储耦合模拟研究，不仅实现了对增强型地热系统的完整性评价，还得出一项重要结论——注、采井的开孔长度对系统产能与寿命会产生重要影响，根据4种开孔长度的算例结果，L0=400 m时是最佳开孔长度，此时系统具有最佳出力与寿命，且在井筒壁上加保温材料可以有效提高开采初、前期采出温度，以减少热损失，提高开采速率。

图10 裂隙渗透率影响采出温度及热开采速率曲线图

图11 裂隙宽度影响采出温度及热开采速率曲线图

2）开采初期，渗流主要在裂隙中，不连通裂隙对渗流及传热影响较小，使得注入井周围出现明显低温区，随时间增加，低温区逐渐沿裂隙通道向采出井方向推移，并且范围越来越大，到后期，低温区蔓延至采出井，不连通裂隙对岩石的传热也已经进行。温度的传播过程始于裂隙通道，进而扩展到整个人工热储层区域，这时应停止开采一段时间，待储层热量恢复后，才能继续维持较长时间的地热资源提取。

3）裂隙渗透率、裂隙宽度等参数对开采速率的影响都呈现正相关性，即随参数值增大，达到最大采出温度的时间缩短，提高了热开采速率，降低了开采年限。