基于蒙特卡洛法的集装箱堆场危险品爆炸威力计算模型
陈武争, 陈大鹏, 陈 力, 张婧卿, 方 秦
(1. 上海中交水运设计研究有限公司, 上海 200092;2. 陆军工程大学 爆炸冲击防灾减灾国家重点实验室, 南京 210014;3. 上海国际港务(集团)股份有限公司,上海 200092)
危险品集装箱堆场是维持工业生产和城市运行的重要基础设施,由于大多数危险品具有显著的易燃、易爆特性,因此,危险品堆场必须进行爆炸安全规划与防护设计。天津港危险品仓库“8.12”特大爆炸事故发生后,危险品集装箱堆场的选址、安全防护设计也越来越引起社会各界的重视,但目前我国尚未建立完善的针对危险品集装箱堆场的规范体系,特别是设计阶段的标准、规范很不全面[1],尤其缺少危险品爆炸威力的计算方法和参数。现有的爆炸相关研究多集中在军事工程方面,民用领域的研究十分薄弱。
通过等效TNT当量系数来描述爆炸物的爆炸威力是一类比较常见的方法。郝新红等[2]提出了一种新的基于AutoReaGas的烟火药爆炸数值模拟方法,得到了烟火药在不同比例爆距下的TNT当量系数。阳建红等[3]通过10 kg TNT炸药和NEPE(Nitrate Ester Plasticized Polyether Propellant)高能推进剂的空中爆炸试验,计算出NEPE高能推进剂在超压为0.006~0.5 MPa范围内的TNT当量系数为1.26。王肇中等[4]通过弹道抛掷法,量测了多种工业炸药的做功能力及TNT当量系数,但由于场地限制,很难广泛应用。王建灵等[5]通过热刺激和机械刺激试验,获得了叠氮硝胺在不同刺激下的响应特征,确定在0.02~0.3 MPa峰值超压范围内,叠氮硝胺TNT当量系数为0.4~0.6。胡宏伟等[6]开展了多种非理想爆炸物在混凝土介质内的爆炸试验,通过测量爆炸在混凝土内部产生的腔体体积来计算不同爆炸物的TNT当量系数。胡广霞等[7]通过对某危险货物集装箱堆场进行研究,通过理论分析与数值模拟,确定了堆场内发生爆炸时的TNT当量,但未考虑危险货物种类及堆存的随机性。陈虹丽[8]以某烟花爆炸仓库为例,基于等效TNT当量分析,从冲击波及废气污染物扩散等方面对爆炸威力进行了分析和预测。可以看出,现有研究大多针对某一特定危险品或已知种类和数量的几类危险品的混合物。实际上,由于港口集装箱堆场多为中转堆场,堆存货物虽有类别限制和场地区域划分,但同一类别下不同种类货物众多。堆场内危险品种类和堆存量很难用单一或固定的指标去描述,因此,准确预测拥有巨大吞吐量和随机危险品种类的集装箱堆场的爆炸威力困难重重。
另外一类常见的爆炸威力计算方法可以不区分炸药种类,而是根据爆炸后果进行分析评价,再与TNT爆炸后果进行类比[9]。如地震波数据推算法[10],爆炸成坑特征推算法[11]和建筑毁伤程度推算法[12-14]。此类方法针对爆炸事故进行评估,基于事故形成的可追溯特征推算存储货物爆炸威力。但此时爆炸灾害已经发生,破坏后果已形成,仍然难以适用于堆场的爆炸安全设计。
本文针对危险品集装箱堆场危险品量大且随机性强这一特点,结合我国东部沿海地区某一超大规模危险品集装箱堆场的设计建设需求,基于蒙特卡洛法,建立了一种概率相关的适用于集装箱堆场的危险品等效TNT当量的计算模型,并针对1类危险品讨论了最大当量系数和防护概率等关键参数的影响,为工程相关的安全防护设施设计、周边重要设施保护提供了理论方法和计算途径。
1 国内外危险品集装箱堆场现状
国内外危险品集装箱堆场堆存方式主要有两种:集中堆存和分散堆存(见图1)。
国外危险品集装箱堆场大多采用分散堆存方式,便于分散风险,不同种类的集装箱之间多采用低价值集装箱、空箱、存储物品易与危险品产生中和反应的集装箱相隔离。此类堆场如发生事故,多为小规模点状事故,不易引起连锁反应,事故等级和规模相对较小,产生的危害和造成的损失也较小。但同时也会带来装卸管理、监管等比较困难的问题。
国内危险品集装箱堆场主要以集中堆存为主[15],在港口外建设专业的堆场,以满足危险品堆存、装卸、监管、安全等各种要求[16]。由于国内是集中堆存,堆场一旦发生爆炸事故极易引发连锁反应,且港外集中堆存的安全防护设计比一般港内危险品堆场要求更高。根据《危险货物分类和品名编号:GB 6944—2012》,危险品一般可划分为1类~9类,1类危险品箱存储的危险品均为极不稳定的易燃易爆品,相对其他种类危险品来说,其伤害更直接、迅速,伤害范围更大[17]。一般来说,此类集装箱宜单独存放,并进行抗爆防护设计,建设抗爆围墙。因此,如何确定危险品堆场的爆炸威力显得至关重要。
2 基于概率的堆场爆炸威力计算模型
2.1 危险品集装箱堆场工况
我国东部某超大规模危险品集装箱堆场规划堆存1类~6类和8类~9类危险品,各类集装箱在周边港口卸船后由集装箱卡车运至该堆场进行堆存、拆装箱或拼箱作业,堆存周期相对较长。危险品发生意外爆炸是该堆场可能发生的重大危险事故之一。根据规划,1类危险品箱集中堆放至堆场东南角区域,需进行抗爆防护设计计算并建设相应的抗爆围墙,如图2所示。

图2 危险品集装箱堆场示意图Fig.2 Schematic diagram of the dangerous goods container yard
在图2的危险品集装箱堆场中,1类危险品区域设计平面箱位40 TEU,堆高两层,最大容量80 TEU,常态容量60 TEU。1 TEU集装箱容积为长609 cm×244 cm×259 cm,内容积为569 cm×213 cm×218 cm,配货毛重质量一般为17.5 t。TEU(Twenty-feet Equivalent Unit)表示长度为609 cm的国际标准集装箱单位。由于该堆场所处区域周边港口拥有着巨大的集装箱吞吐量,导致该堆场堆放的1类危险品的种类及数量具有非常大的不确定性。
2.2 随机模拟方法
随机模拟法又称蒙特卡洛(Monte Carlo)法,是一种通过设定随机过程,反复生成时间序列,计算参数估计量和统计量,进而研究其分布特征的方法。具体来说,当系统中各个单元的可靠性特征量已知,但系统的可靠性过于复杂,难以建立可靠性预计的精确数学模型或模型太复杂而不便应用时,可用随机模拟法近似计算出系统可靠性的预计值。随着模拟次数的增多,其预计精度也逐渐增高,在不断对某一过程进行模拟时,可通过预计值落在某一范围内的次数与模拟总次数的比值来近似确定预计值落在该范围的概率。由于涉及到随机过程的反复多次生成,蒙特卡洛模拟法是以高容量和高速度的计算机为前提条件的,因此只是在近些年才得到广泛推广。相比于传统的数学统计方法,蒙特卡洛法可以通过借助计算机来减少人为计算的困难,且可操作性强,直观易懂[18]。
2.3 理论计算模型
仍然选择通过等效TNT当量来表征危险品的爆炸威力。通过对该危险品集装箱堆场周边港口1类危险品(爆炸品)进行统计,将未来拟堆存在该项目堆场内的爆炸品分为A~E五小类,分别对应《危险货物分类和品名编号》中的1.1项~1.5项。由于危险品爆炸产生的能量等于危险品的质量与其爆热的乘积,可通过能量相似理论计算出各种危险品的等效TNT当量。假设每一小类危险品的TNT当量系数、密度和体积分别为γi,ρi,Vi(i取1~5),则1类危险品的TNT当量可表示为
(1)
对于同一小类爆炸物,γi,ρi均可视为常数,因此可以引入一个新的转换系数物理量αi=γiρi,量纲与ρi相同,表示单位体积的危险品i,可以等效为质量为αi的TNT炸药。则此时式(1)可以转化为
(2)
取αmax=max{αi},αmin=min{αi},则
Mmax=αmaxV,Mmin=αminV
(3)
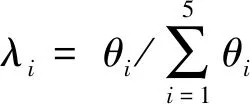
(4)
蒙特卡洛法的误差通常可以表示为[19]
(5)
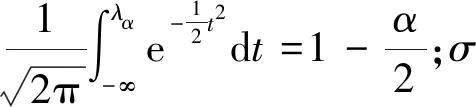
对于一般工程,随机数n通常取3 000~5 000[20]即可满足工程精度要求。为了提高精度,分别取n=103,n=104,n=105,n=106,计算等效TNT当量随机分布值M的均值与标准差,每组模拟次数n进行三次计算,得表1。
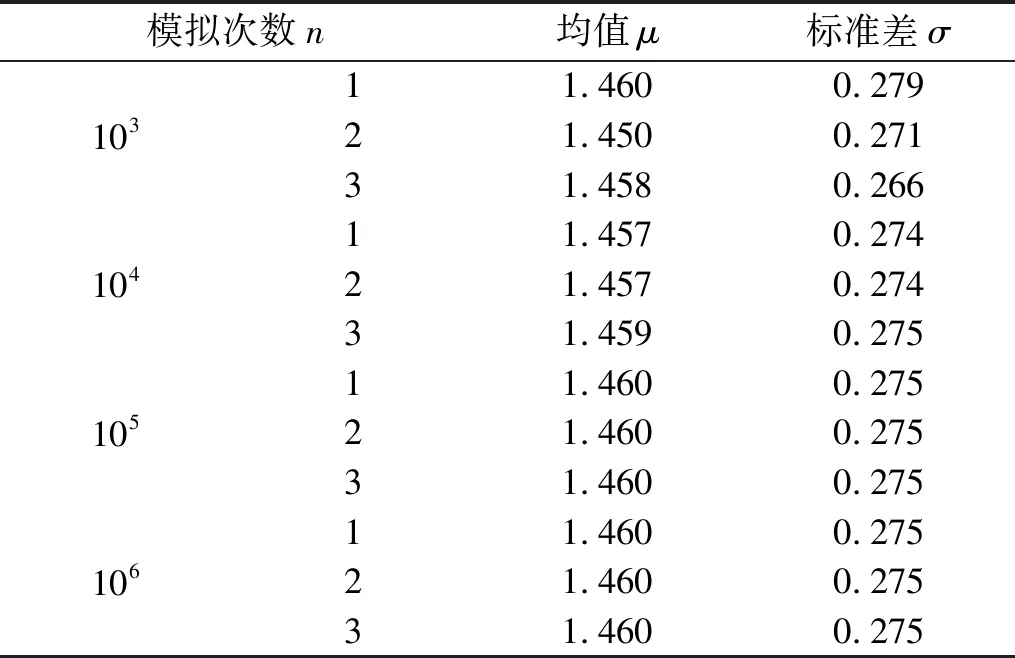
表1 不同模拟次数下的均值及标准差Tab.1 Mean value and standard deviation after different simulations
从表1可知,n=104,n=105,n=106时,标准差σ稳定在0.275,故取σ=0.275。由正态分布表可知,显著水平α=0.01时,λα=2.575 8,若控制误差ε在0.1%量级,由式(5)计算可得n=5.01×105,故n>5.01×105时才能保证误差控制在0.1%范围内,故取模拟次数n=1×106。
通过MATLAB完成n=106组随机数的产生,利用式(4)计算出各组随机数下的等效TNT当量Mi(i=1,2,…,106)。等效TNT当量随机分布值计算框图,如图3所示。
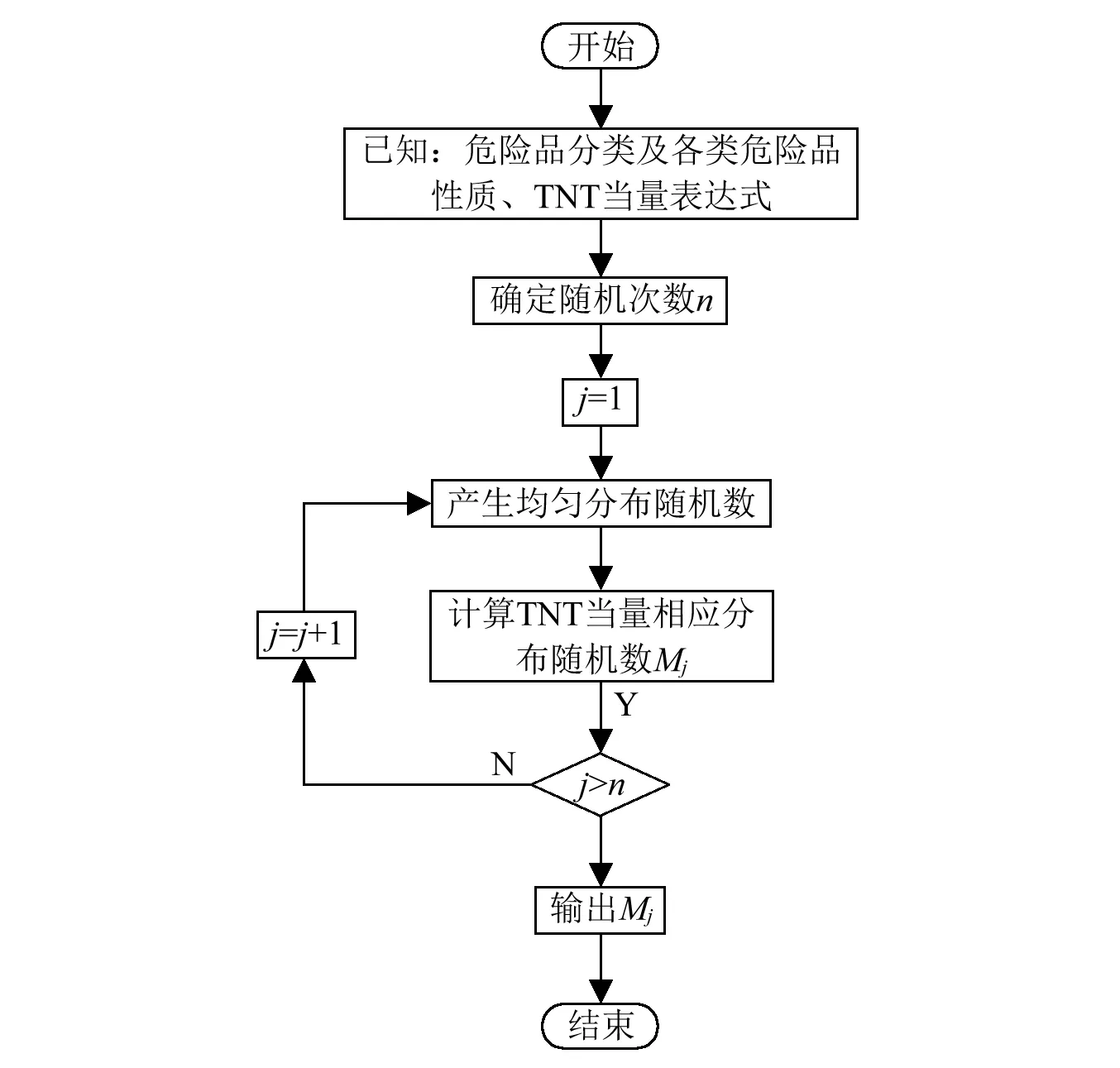
图3 计算流程框图Fig.3 Flow chart of calculation process
由式(3)可知,M的取值范围为[αminV,αmaxV]。任取[αminV,αmaxV]范围内的两个数φ1,φ2,不妨设φ1<φ2。TNT当量值M落在区间[φ1,φ2]的概率,等于M落在区间[φ1,φ2]的样本个数nφ1,φ2与总样本数n的比值,即
(6)
堆场危险品等效TNT当量随机分布值M为离散型随机变量,由于样本容量n足够大,可近似认为M为连续型变量。令f(M)概率密度函数,简称概率密度。则
(7)
若不计高阶无穷小,则:p(M1 (8) 由此可以根据式(8)构造概率密度函数分布图,根据其分布特征和概率需求,确定危险品堆场的等效TNT当量M。假设M′表示堆场等效TNT当量的设计值。当爆炸事故发生时,堆存危险品的等效TNT当量真实值不大于设计值M′时,认为防护工程可以完成防护任务,即达到有效防护,TNT当量真实值不大于设计值的概率可称为有效防护概率pe。在根据TNT当量做防护设计时,为求保险,可以采用TNT当量的最大值Mmax来进行设计,即M′=Mmax,此时有效防护概率为100%。将有效防护概率适当降低,在不影响防护效果的同时,等效TNT当量设计值也将降低,从而达到节约防护成本的目的。 常见民用危险品的等效TNT当量系数范围为0~1.5,密度为1~2 g/cm3[21]。由于αi=γiρi,故转换系数α的范围为0~3。为了更具一般性,取[0,3]中的五个随机数(0.2,0.7,1.3,2.3,2.8)作为五种爆炸品的转换系数,即(α1,α2,α3,α4,α5)=(0.2,0.7,1.3,2.3,2.8)。为方便计算,取堆场容量V=1,则Mmax=2.8,Mmin=0.2。 取区间(0,0.01],(0.01,0.02],…,(2.99,3],通过式(5)分别求出各区间内的概率,并由式(8)求出概率密度f(M)的分布,如图4所示。由图4可知,此时TNT当量M近似于正态分布。 图4 TNT当量计算值分布Fig.4 TNT equivalent value distribution 求出样本中M的均值,标准差分别为:μ=1.460,σ=0.354并画出均值μ=1.460,标准差σ=0.354的正态分布图,并与TNT当量计算值分布图进行比较,结果见图5,比较结果也证明了通常情况下,堆场危险品TNT当量随机值应该符合正态分布。 图5 随机模拟值与相应正态分布比较Fig.5 Comparison between the random simulation value and the corresponding normal distribution 由于M服从于μ=1.460,σ=0.354的正态分布,故(M-μ)/σ服从于标准正态分布。查标准正态分布表,可得堆场的有效防护概率pe=[(M-μ)/σ<(M′-μ)/σ]=0.9时,(M′-μ)/σ=1.28,即堆场的危险品等效TNT当量设计值M′=1.91。定义λ为 (9) 可以看出,当此工况的有效防护概率由100%降到90%时,等效TNT当量设计值由Mmax=2.8降到M′=1.91,降低了31.8%,相应的工程防护设计建设成本也会相应下降。 经过多组转换系数的计算发现,当有效防护概率由100%降到90%时,TNT当量设计值下降的百分比是随着不同工况发生变化的。由式(9)可知,在计算TNT当量设计值下降比例λ时,Mmax对计算结果产生很大的影响。由于总体积V是定值,根据式(3)可知,最大转换系数αmax是Mmax的关键参数。η表示最大转化系数αmax与其余四个转化系数之和的比值,即 (10) 式中:η的取值范围为[0.25,∞),η取到0.25的情况为五个转换系数相等。例如:α1=α2=α3=α4=α5=1;η趋于无穷的情况为最大转化系数为常数,而另外四个转化系数之和趋于0时。为研究η的取值对下降比例λ的影响,分别取η=0.5,η=1,η=2,η=4,η=8进行讨论。当α1=α2=α3=α4=0.1,α5=0.2时,η=0.5,由2.3中的方法求出概率密度f(M)的分布,得出此时的均值μ=0.12,标准差σ=0.011。等效TNT当量计算值与μ=0.12,σ=0.011的正态分布的比较如图6所示。 图6 随机模拟值与相应正态分布比较(η=0.5)Fig.6 Comparison between the random simulation value and the corresponding normal distribution at η=0.5 表2 各工况下降比例λ计算表Tab.2 Calculation table of decreasing ratio λ for each working condition 由表2可知,η增大时,λ也随之增大。说明最大转化系数与其余四个转化系数之间差距越小,有效防护概率降到90%时,TNT当量设计值下降比例越小;最大转化系数与其余四个转化系数之间差距越大,TNT当量设计值下降比例越大。 继续以东部某超大规模危险品集装箱堆场1类危险品为计算背景,采用提出的爆炸威力计算方法计算该堆场的1类危险品的等效TNT当量。堆场内标准集装箱内部危险品的有效体积(除去货架及外包装的危险品体积)为5 m3,拟堆存的危险货物见表3。 表3 标准箱内拟堆存的危险货物[22]Tab.3 Dangerous goods to be stored in standard case 由表3可知,αmax=1.38 g/cm3,αmin=0.42 g/cm3,则Mmax=6.9 t,Mmin=2.1 t。为使误差控制在0.1%范围内,基于“2.3”节中模拟次数的确定方法,取模拟次数n=106。通过MATLAB实现计算出106组TNT当量Mi(i=1,2,…,106)的随机分布值,取区间(2.1,2.11],(2.11,2.12],…,(6.89,6.9],基于“3.1”节中的计算结论,认为此时TNT当量随机分布值Mi服从于μ=4.630,σ=0.582的正态分布,故(M-μ)/σ服从于标准正态分布。查标准正态分布表,可得有效防护概率p[(M-μ)/σ<(M′-μ)/σ]=0.9时,(M′-μ)/σ=1.28。既而,得出该集装箱的危险品等效TNT当量设计值为M′=5.37 t。 本文针对危险品集装箱堆场的等效TNT当量开展研究,考虑了堆存危险品种类及数量的不确定性,建立了一种概率相关的爆炸威力计算模型,并结合工程建设算例,讨论了防护概率和最大转化系数对TNT当量设计值的影响规律,主要结论有: (1)堆场内随机堆放1类危险品时,等效TNT当量值基本符合正态分布。 (2)将1类危险品的有效防护概率由100%降到90%时,等效TNT当量设计值可下降30%~70%,在不影响有效防护的同时,可大大降低设计和建造成本。 (3)不同种类危险品最大转化系数与其余转化系数之间的差距越大,等效TNT当量设计值下降越明显。3 关键参数讨论
3.1 有效防护概率pe
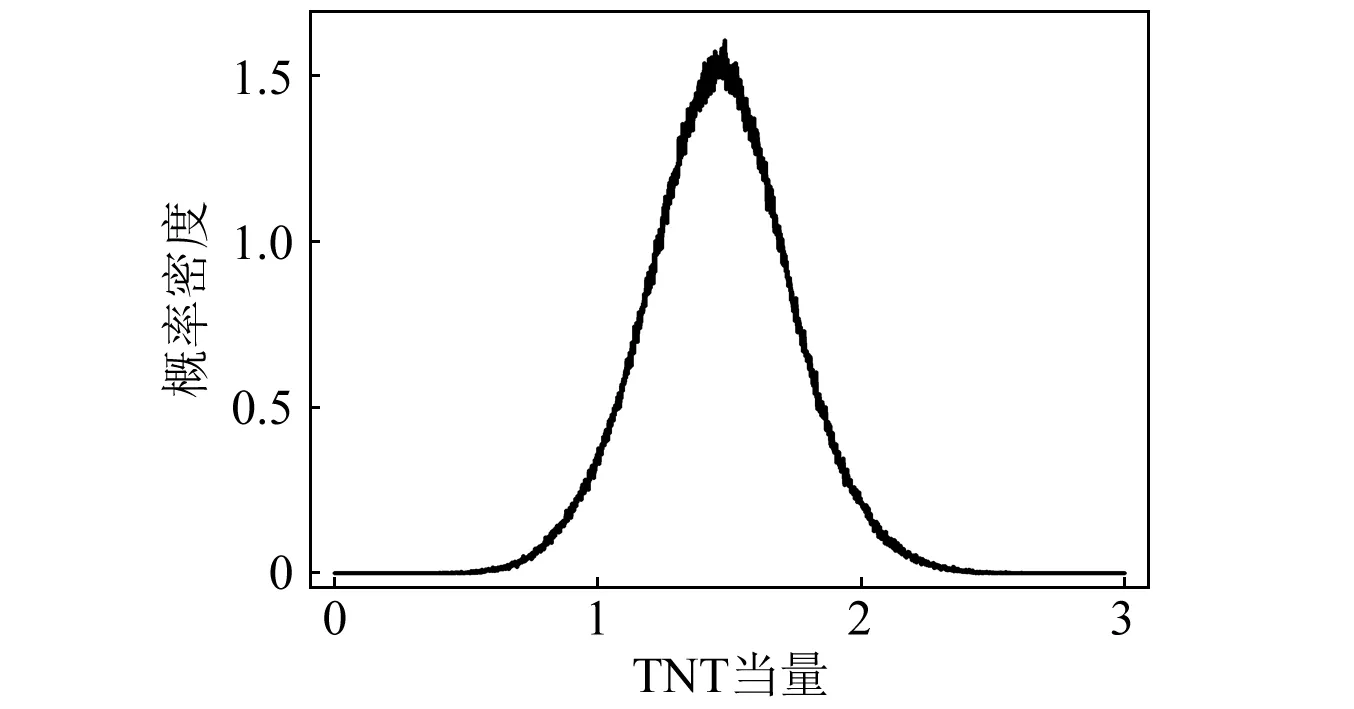
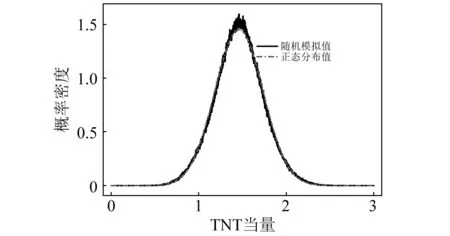
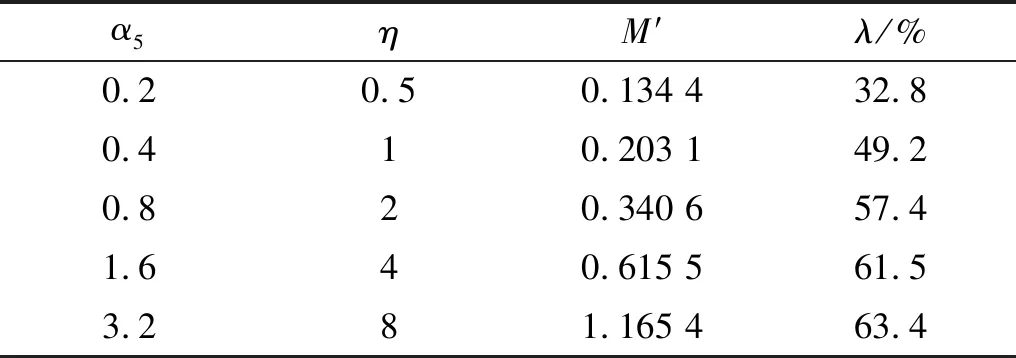
3.2 最大转换系数

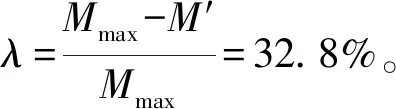
4 工程计算案例

5 结 论

