考虑轮轨接触损失的列车乘员舒适性分析
张经纬, 刘学文, 王岩松, 王颖轶
(1.上海工程技术大学 机械与汽车工程学院,上海 201620;2.上海交通大学 船舶海洋与建筑工程学院,上海 200240)
轨道交通是城市发展的动脉,其便携性和舒适性的提升直接关系着轨道交通在市场竞争中的地位[1-2],因而,研究轨道交通特别是车-线-桥耦合振动下的列车乘员舒适性就显得尤其重要。
国内外关于车-线-桥耦合振动的研究,已经进行了许多有意义的工作。文献[3]建立了简易的单轮对CRH5动车组模型,基于德国的高干扰谱、低干扰谱及英国的小缺陷谱进行了车体舒适性的对比分析;文献[4]建立了9自由度的车辆空间模型,在轮轨始终接触的假设下,通过位移和力的协调条件与桥梁耦合成车桥耦合系统,对车体的振动响应及舒适性进行研究;文献[5]建立了三维的四轴23自由度和六轴27自由度车辆模型,在轮对不跳轨的前提下,利用轮轨间的几何相容条件和静力平衡条件与桥梁耦合成大系统,对车体的动力响应及乘坐舒适性进行分析;文献[6]在经典的10自由度车辆模型的基础上,将人体用8个自由度的多刚体块模拟,建立了三维空间多自由度的人-车耦合模型来分析乘员的舒适性,但文中没有说明单个人体在整个三维模型中的处理方法,在车-桥耦合系统中,单个人体质量相对车体和桥体质量很微小,算法上难以体现出其差异,且人体模型选取对计算结果影响很大;文献[7]在经典的10自由度车辆模型的基础上,将一节列车车厢的乘员分成十排,用10个等效质量块模拟,基于地面激励,结合经典10自由度车辆模型,建立了人-车耦合动力模型,并用Fortran编写程序计算分析了乘客和车体的舒适性振动差异;文献[8]基于经典10自由度车辆模型,结合双层轨道浮置板桥梁结构建立车桥耦合振动大系统,并提出了一种半解析解的计算方法来解决车轮跳跃的工况,对车体和桥体的振动响应进行了分析;文献[9-10]中指出台湾和法国国家铁路公司(SNCF)的列车舒适性限值为垂向最大加速度小于0.49 m/s2;欧洲规范目录[11]中指出列车舒适性限值为垂向最大加速度小于1.0 m/s2;根据我国《铁路车辆动力学性能评定和试验鉴定规范》中的规定,列车舒适性限值是垂向最大加速度小于2.5 m/s2。
上述研究都侧重于车体振动响应和舒适性的分析,并主要以轮轨始终接触为计算前提。人车-桥耦合振动系统的乘员舒适性问题较为复杂,涉及主观和客观因素,而主观舒适性的评价因人而异,难以形成统一的标准,因此客观因素的定量分析就有待于进一步研究[12]。本文基于以往研究的基础,做一些新的探索。从列车在高架铁路运行的角度出发,考虑轮轨瞬时脱离工况,引用动态单元法[13],来处理轮对和轨道之间的耦合作用,以列车和乘员为研究对象,基于经典10自由度车辆模型及轮轨瞬时脱离工况建立一个半空间13自由度人车等效计算模型,分别计算不同速度、不同轨道不平顺谱下的车体及乘员动力响应,并对车体和乘员舒适性差异进行定量分析。
1 物理模型及各轨道不平顺下车辆动载荷
本文采用半空间13自由度人-车模型来模拟车辆和乘员的振动,并对该模型作以下假设:
(1) 只考虑人体、车体的垂向振动;
(2) 人车动力系统采用13自由度动力模型;
(3) 列车以恒定速度运行;
(4) 各个车体之间的纵向力不做考虑;
(5) 考虑轮轨瞬时脱离的工况;
(6) 假设满车厢乘员为99人,人均体重75 kg,用集中质量法,将整车厢乘员等效成3个等效刚体质量块。
模型如图1所示。经典10自由度模型[14]中,将车体视为质量为Mc的刚体,有浮沉运动和仰俯运动两个自由度位移分别为zc,φc,车体转动惯量为Jc;前后两个转向架分别视为质量为Mt的刚体,也有浮沉运动和仰俯运动两个自由度分别为zti,φti,i=1,2,i为前后转向架,转向架转动惯量为Jt;4个轮子则被视为只考虑浮沉运动的质量为Mw的刚体,其位移为zwi,i=1~4,i表示第i个轮对;本文建立的13自由度模型考虑到单个人体的质量问题,其相对于车体质量可以忽略不计,在数学建模中,无法进行精确的计算,所以,本文用集中质量等效法,将一整车厢的乘员,平均集中质量到3个特殊点上进行计算,3个特殊点分别是:车体和转向架耦合的前后两个点,车体的正中间点,以及整个车厢的其他任意一点,均可用插值法得到,其质量为Mpi,i为第i个等效质量块,3个等效人体各有且仅有一个自由度,耦合刚度和阻尼分别记做kpi,cpi,i=1~3。
采用美国联邦铁路管理局(FRA)不平顺功率谱密度来描述路面随机不平整度特性,其高低不平顺拟合表达式
(1)
式中:Sv(φ)为轨道不平顺功率谱密度,m2/(1/m);φ为轨道不平顺的空间频率,m-1;Av为粗糙度常数,m;φv1,φv2是截断频率,m-1;下标V为垂向,即高低方向。轨道级别分为六级,具体轨道级别的粗糙度参数及截断频率参见文献[15]。
采用适当的时频转换方法,将轨道随机不平顺功率谱密度函数转换成随线路里程变化的轨道不平顺空间样本,将该样本代入式(14),用Newmark-β法编制C++程序,即可对各等级轨道不平顺条件下的人-车-桥耦合振动方程进行求解。车辆在各个轨道不平顺下的动载荷可由式(6)得出,其具体公式见“2”节。
2 人-车-线系统耦合动力数学模型
2.1 半空间垂向13自由度人-车动力数学模型
引起乘员、车辆和轨道、桥梁系统之间动态反馈作用的直接原因就是轮对和钢轨的振动变形进而引起轮轨接触变形及接触几何状态变化而产生的作用,因此要确定耦合模型的振动方程,首先要确定轮轨之间的关系。为简便计算,本文只计算一节车厢。
轮对沉浮振动方程定义为
(2)
(3)
(4)
(5)
式中:pi为轮轨之间的耦合力,上标“.”为对时间求一次导数;上标 “..”为对时间求两次导数,下文不重复说明。
pi=Kh(zwi-zb(x,t)|x=vt+Irr)
i=1~4
(6)
式中:i为第i个;zb(x,t)|x=vt为t时刻第一轮对正下方结构(轨道或者桥梁)的竖向位移;Irr为该处结构的不平顺值;Kh为轨道接触刚度。
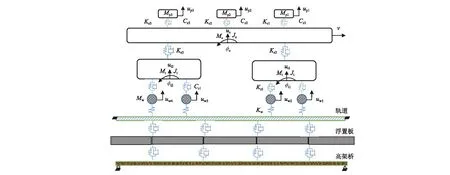
图1 半空间13自由度人车-线耦合动力模型Fig.1 Half space 13 DOF human-train line interaction model

(7)
经典的车辆振动模型此处不再赘述,直接介绍等效人体振动公式部分。
人体受力分析如图2所示。其中Fcp1,Fcp2和Fcp3分别为车体前、中、后耦合点对等效人体的作用力,其表达式分别为
(8)
(9)
(10)
其中,
kp1=kp2=kp3,Cp1=Cp2=Cp3,Mp1=Mp2=Mp3。人体沉浮振动方程
(11)
(12)
(13)
结合传统半空间10自由度车体振动方程,可写出人-车系统模型的动力方程
(14)

Qv=[0,0,0,0,0,0,aMw1g-F1,aMw2g-F2,
aMw3g-F3,aMw4g-F4,0,0,0]
(15)
u={zcφezt1φt1zt2φt2zw1
zw2zw3zw4zp1zp2zp3}
(16)
(17)
(18)
Mv=diag{McJcMtJtMtJtMw1Mw2
Mw3Mw4Mp1Mp2Mp3}
(19)
其中,

(20)
13自由度模型矩阵中车体部分具体参数不再赘述,具体参见Liu等附录A中车体参数。
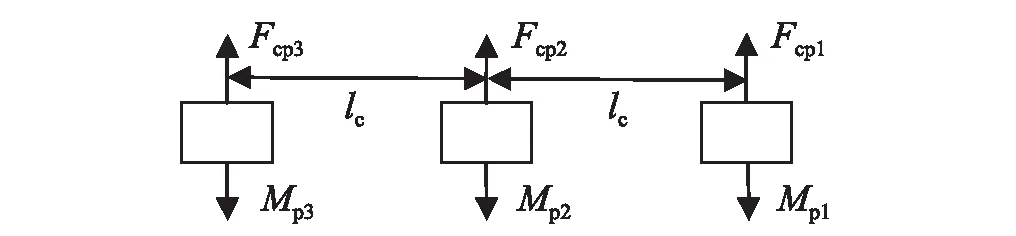
图2 等效人体受力分析图示Fig.2 Equaivalent humans force diagram
2.2 轮轨瞬时脱离工况分析
列车在实际线路运营中,由于轮轨基础刚度突变、钢轨磨损或尖端不平顺等因素的存在,会引发车轮跳离钢轨的现象,在此期间,车轮与轨道之间并不是一直处于接触的状态,而是会随着轮轨间压缩量的变化而变化。本文将这种现象称为轮轨接触损失,同时将轮轨间发生瞬时跳跃的工况细化,先判断再计算,具体方法参见刘学文的研究。
图2给出了考虑轮轨瞬时脱离工况时,轮轨接触弹簧,在不同阶段的不同状态。如图3所示,Line 1表示弹簧的原始状态,Line 2表示弹簧的静平衡状态,图中的数字代表不同的弹簧状态。当轮轨接触弹簧的状态不同时,车体和桥体这两个子系统之间的作用力也会跟着变化,变化状态如表1所示。

表1 车桥受力的各种不同状态
2.3 桥梁振动响应方程
本文的人-车-桥耦合系统模型中,线-桥下部耦合系统结构并不是使用简单的单简支梁,而是引用了轨道、浮置板及桥梁双层振动模型,其中轨道和桥梁等下部结构均简化为欧拉梁,浮置板则简化为刚体质量块结构,其具体振动响应方程及模型参见刘文学的研究。

图3 车轮瞬时脱离的不同状态Fig.3 Different states of moving wheel jumping from rail
3 模型参数、算法及验证
3.1 车体、人体模型参数
选取高铁列车模型和高架桥常用的近似数据,下部结构参数,参见刘学文研究中的双层带浮置板的模型。
3.2 模型程序算法
半解析解法的工作流程如下所示,其中所用到的Newmark-β法中的两个系数分别为γ=0.505,β=0.252 506 25:
步骤1推导出人体的广义质量矩阵、广义阻尼矩阵以及广义刚度矩阵;
步骤2推导出车体的广义质量矩阵、广义阻尼矩阵以及广义刚度矩阵;
步骤3推导出桥梁的广义质量矩阵、广义阻尼矩阵以及广义刚度矩阵;
步骤4时间循环;
步骤5每个时间步中的迭代精度计算循环;
步骤6耦合刚度及耦合力置0;
步骤7轮对循环;
步骤8计算第i个轮对的位置;
步骤9判断轮对是否在桥梁上,当轮对在桥上时,则先判断其接触状态,再进行计算;当轮对不在桥上时,则做非桥梁部分计算;
步骤10计算耦合刚度及耦合力;
步骤11结束轮对循环;
步骤12调用Newmark-β法对形成矩阵进行求解;
步骤13判断收敛,收敛转步骤14,不收敛转步骤4;
步骤14结束时间循环;
步骤15输出结果。
3.3 模型验证
振动测试地点:上海地铁5号线,莘闵线,银都路站西320 m。本文的模型与上海轨道交通5号线有所差异,所以采用退化模型进行仿真计算,具体退化模型的采用是将浮置板下的支座弹簧刚度和阻尼增大,用较大的刚度和零阻尼来模拟实际结构中的支承块跟高架直接连接的结构,而其他结构比如轨道,轨道和浮置板之间的扣件刚度、阻尼,都与轨道交通5号线形式保持一致,其具体数据如下:
列车速度v=60 km/H;轨道不平顺谱选择美国六级谱;轨道采用重型钢轨60 kg/m,轨道的弹性模量Er=2.1×1011Pa,轨道的横截面积Ar=7.708×10-3m2,轨道的惯性矩Ir=3.203×10-5m4,轨道和浮置板之间的扣件、垫板刚度为4.5×107N/m,阻尼为8.433×105N·s/m,承轨台(即退化模型前的浮置板)质量为1 500 kg/单线延米,浮置板与桥梁之间的刚度取4.5×1011N/m,无阻尼,单元长度0.6 m,承轨台在模型中用刚体质量块表示;高架桥用简支梁;时间步长为0.000 5 s,轨道参数为:60 kg/m,长46.4 m。将这些参数输入到编制的C++程序中进行求解,得到该路段通车后的轨道振动的计算值,并与实测值进行对比,如图4和图5所示。

图4 钢轨竖向振动加速度实测值(v=60.0 km/h) Fig.4 Measured vertical vibration of rail (v=60.0 km/h)
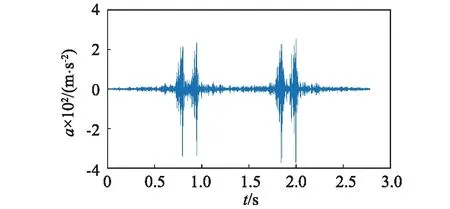
图5 轨道垂向振动加速度计算值(v=60.0km/h)Fig.5 Calculated vertical vibration of rail (v=60.0 km/h)
取高架桥跨中处钢轨的垂向振动加速度为研究对象,其中图4是实测结果图,图5为本文仿真计算所得结果,两图中的垂向加速度振动峰值,分别为对应的单节车厢两车轴下四副轮对经过轨道跨中时该处轨道的振动响应。本文计算值中采用的车轴和车轮间距以及列车行驶速度均与实测一致,所以其峰值的间隔也应一致。出于降低计算量的目的,本文只将一节车厢代入计算,由两图可得,计算结果的峰值和峰值的间隔,与实测结果都很贴近,故与实测值有较好的一致性,从而验证了本文程序和模型的有效性。
4 动态响应及舒适性数值分析
基于上节的分析,以美国轨道不平顺谱为例,分析各轨道不平顺下等效人体Mp1、车体振动的差异,参数如表2所示。
4.1 不同等级不平顺谱下车体、人体的振动响应
取美国三级、四级、五级及六级四种轨道不平顺谱,经参考分析后,选用三角级数法,模拟出来的三级、四级、五级、六级轨道不平顺谱如图6所示[17-20]。桥梁长度不变,仍取46.4 m,以便分析。
列车速度为20 m/s时,对应的四种不平顺工况下列车通过高架桥的整个过程中,车体和耦合点(下文中直接称人体)的振动响应曲线如图7。图7(a)~图7(d)中四种曲线变化趋势相似,可以看出,当轨道不平顺等级越高,车体和人体的垂向振动幅值和垂向振动加速度幅值越大,车体的最大振动位移范围为-1.5×10-3~2.0×10-3m,最大振动加速度范围为-0.4~0.4 m/s2;人体的最大振动位移范围为-2.5×10-3~2.5×10-3m,最大振动加速度范围为-0.5~0.5 m/s2,振动响应有所增大。

图6 四种轨道的质量图谱Fig.6 Profiles for four classes of track quality

图7 不同谱下的车体、人体响应对比Fig.7 Dynamic responses of vehicle and passenger
这一现象导致的结果,将是车体与人体的乘坐舒适性有所差异,乘坐舒适性是高速列车的一个重要指标,而垂向振动加速度就是评价乘坐舒适性的一个重要参数。图8和图9分别给出了四种轨道不平顺谱对应的0~90 m/s速度范围内以5 m/s为增量时,车体和人体最大垂向加速度的变化曲线。
图8中,同一轨道谱下,随着速度的增加,车体的最大垂向振动加速度整体上呈上升的趋势,即速度越高,舒适性越低,这符合我们的通常感受。当轨道不平顺谱等级超过三级,速度在62.5 以上时,车体的最大垂向加速度会超过台湾和法国SNCF的列车乘客舒适性指标为0.49 m/s2(=0.05g),但在欧洲最低标准在1.0 m/s2以内。
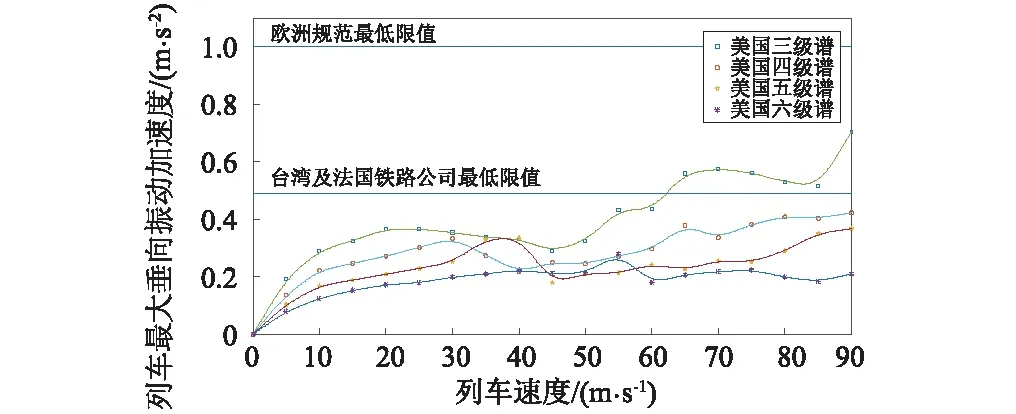
图8 不同谱下车体最大垂向加速度对比Fig.8 Maximum vertical acceleration of the train for four classes

图9 不同谱下人体最大垂向加速度对比Fig.9 Maximum vertical acceleration of passenger for four classes
图9中,同一轨道谱下,随着速度的增加,人体的最大垂向振动加速度整体呈上升的趋势;同一速度下,随着轨道不平顺等级的增加,前耦合点处等效人体的垂向最大振动加速度会变大。当轨道不平顺谱等级为三级,速度在25 m/s时,人体的最大垂向加速度就已经超过舒适性指标0.49 m/s2(=0.05g);当轨道不平顺谱等级为四级,速度在82.5 m/s附近时,人体的最大垂向加速度也超过了0.49 m/s2,但都还在欧洲最低标准1.0 m/s2以内,也低于我国铁路标准2.5 m/s2。
4.2 车体、人体最大加速度对比分析
各速度下,人体、车体垂向最大振动加速度对比曲线,如图10(a)~图10(d)所示。
由图10(a)~图10(d),同一轨道不平顺谱同一速度下,车厢前耦合点处乘员的垂向最大振动加速度值整体要比车体的垂向最大振动加速度要大。其中,六级谱中,人体垂向最大振动加速度比车体垂向最大振动加速度整体增大了15.44%;五级谱中,人体垂向最大振动加速度比车体垂向最大振动加速度整体增大了18.32%;四级谱中,人体垂向最大振动加速度比车体垂向最大振动加速度整体增大了23.96%;三级谱中,人体垂向最大振动加速度比车体垂向最大振动加速度整体增大了22.21%。
六级谱和五级谱虽然增大,但都在台湾和法国SNCF铁路乘员乘坐舒适性指标以内;而四级谱下,如果以车体垂向最大振动加速度计算则满足舒适性指标,但如果以前耦合点处乘员垂向最大振动加速度计算,则在列车速度达到82.5 m/s之后,不满足振动指标;三级谱下,当以车体垂向最大振动加速度为指标时,速度达到65 m/s以后才超出0.49 m/s2的指标,而当以人体垂向最大振动加速度为指标时,速度在25 m/s就超出了0.49 m/s2的指标。
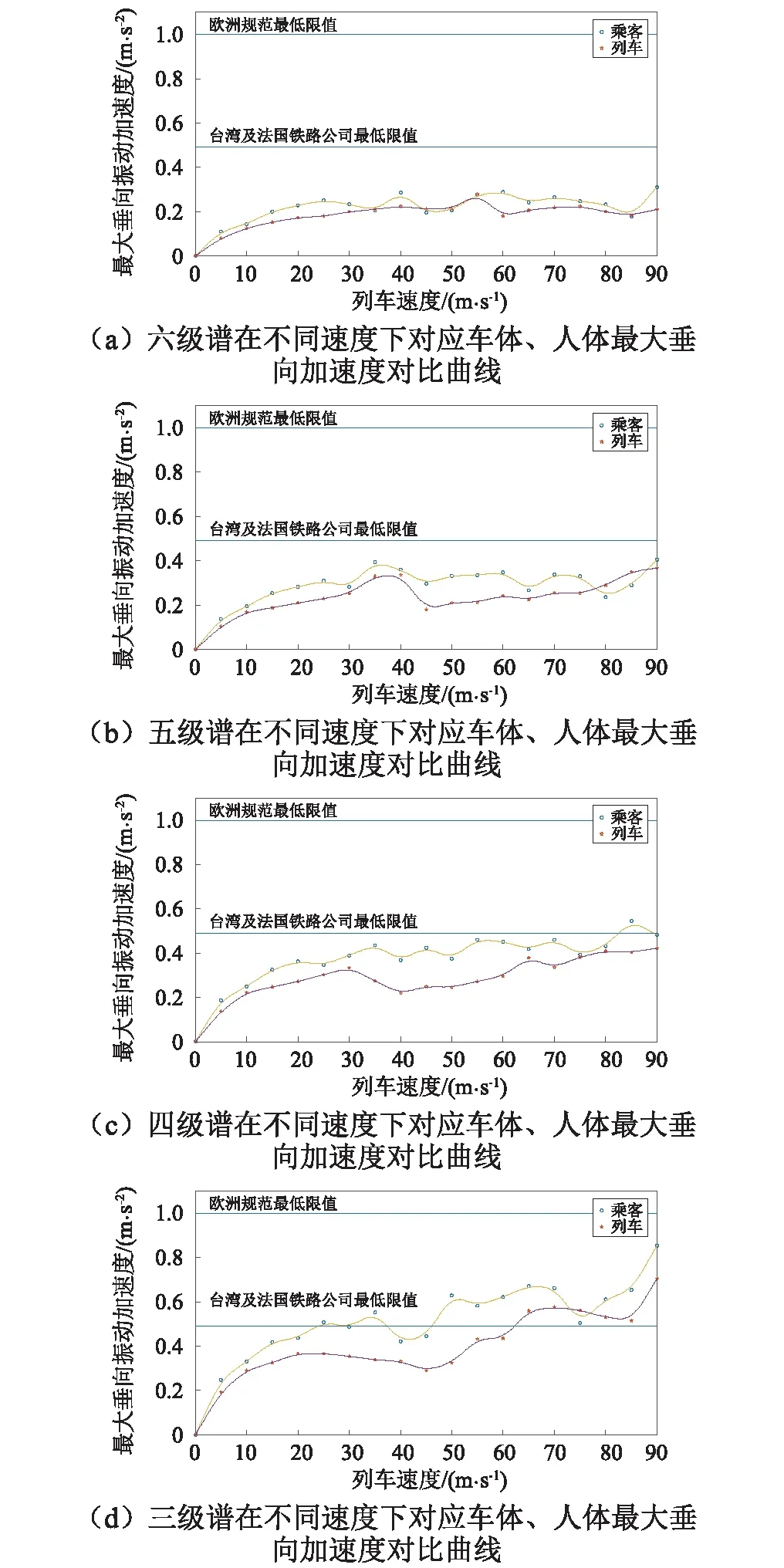
图10 各速度下人体、车体垂向最大振动加速度对比曲线Fig.10 Maximum vertical acceleration curves of vehicle and passenger at each speed
可见,传统的10自由度半空间模型,只能将舒适性指标放在车体上进行计算,但列车实际运行中,人体和车体的振动响应是有所差异的,而且还存在轮轨瞬时脱离的工况,本文建立的13自由度半空间模型,可以将舒适性指标放到人体上进行分析,结果更加准确、更贴近实际。
5 结 论
(1)考虑到单个人体质量相对于车-桥耦合大系统太过微小,算法上难以体现差异,本文基于经典半空间10自由度车-桥耦合动力模型的基础,建立了考虑轮轨接触损失的半空间13自由度的人-车耦合动力模型,用集中质量法将车厢乘员均分成3个质量块,分别集中到车厢与前后两个转向架耦合点处以及车厢中心点处,既在算法上体现出了乘员与车体的振动差异,又避免了将乘客划分成过多个质量块带来的过多计算量。文中3个特殊点以外的任何位置,都可以用插值计算得到其振动响应数值。同时采用C++语言开发了该模型的求解程序。通过将一段实验路段的轨道振动计算值与实测值进行对比,验证了本文模型的有效性。
(2)分别将人体和车体的振动响应作为输入,对列车舒适性进行计算分析。结果表明:随着速度增大和轨道不平顺等级的提高,车体和等效人体的舒适性均会降低,而前耦合点处等效人体的振动响应明显会大于车体。
(3)以往的车桥耦合模型和列车舒适性标准都是以车体振动为标准,但随着高铁的快速发展,以及乘客对高铁舒适性越来越高的要求,使得该标准开始渐渐满足不了市场需求,而本文将13自由度人车-线模型与高架桥耦合,建立人-车-线耦合大系统,并考虑了车轮和轨道之间的轮轨接触损失工况,能够同时计算出车体和等效人体的振动舒适性,更贴近实际,且更能满足高标准的舒适性计算要求。
(4)本文的人-车耦合模型仅建立在垂向半空间之内,有所简化,而实际列车运行需要考虑整个空间的横向、纵向,这也是后续研究的方向。

