滚珠丝杠进给系统动力学建模与动态特性分析

付振彪， 王太勇， 张 雷， 杨 倩

(1.天津大学 机械工程学院，天津 300072; 2.北京工业大学 应用数理学院，北京 100124)

滚珠丝杠进给系统是数控机床进给系统最常见的形式之一，其动态特性对机床的整机性能、加工精度和质量有着重要影响[1]。近20年来，数控机床不断向着高速、高精密方向发展，这对机床进给系统的动态性能和稳定性提出了更高的要求。因此深入研究滚珠丝杠进给系统的建模方法和动态特性是非常必要的。

近年来，国内外众多学者对滚珠丝杠进给系统进行了动力学建模与分析。文献[2-5]考虑了滚珠丝杠副的接触刚度，基于集中质量参数法研究了进给系统的振动特性。文献[6-8]考虑了导轨的线性刚度和预紧力的影响，基于有限元法研究了进给系统的动态特性。文献[9]建立了某测量机Z轴滚珠丝杠进给系统的动力学模型，基于该模型设计了控制系统的误差补偿方案，其所建立的动力学模型并未考虑滚动导轨副的接触刚度；然而，滚动导轨副的接触刚度对进给系统的动态特性有着重要影响。文献[10-11]考虑了滚动导轨副预紧力的影响，研究了主轴的动态性能，但是对于滚动导轨副的接触刚度缺乏更深入的研究。此外，文献[12-13]应用不同的方法研究了主轴的动态特性，其动力学模型包含了轴承接触刚度、主轴、切削刀具以及整个床身的动态变形，但是没有考虑滚珠丝杠进给系统各结合面的接触刚度。文献[14]基于ISIGHT软件，搭建了机床整机结构方案设计的系统框架，实现了以静动态特性和质量为目标的结构优化设计，但是在整机结构建模时，对于进给系统众多结合面进行了大量简化。文献[15]针对滚珠丝杠进给系统结合部刚度难以确定的问题，提出了基于Hertz接触理论的计算方法，建立进给系统的有限元模型，但是基于Hertz接触理论的计算方法不够准确，有限元建模时忽略了联轴器和滚珠丝杠的扭转刚度，建模方法有待改善。

综上所述，对于滚珠丝杠进给系统的动力学建模，关键在于各结合面的建模和仿真，而现有的研究中对各结合面的刚度计算、动力学建模和有限元仿真还很不充分。本文综合考虑滚珠丝杠进给系统中各结合面的影响，提出了一种有限元建模方法。将滚珠丝杠副、滚动导轨副、轴承简化为弹簧-质量模型，基于Hertz接触公式的一阶求导，推导了各结合面接触刚度的计算公式，求出了当前接触状态下的接触刚度值。此外，考虑了丝杠轴和联轴器的扭转刚度的影响，利用有限元软件建立了整个进给系统的动力学模型。采用多单元混合的方法进行网格划分，仿真分析了承载台的前五阶模态振型和固有频率。通过模态试验对有限元仿真结果进行了验证。应用该模型着重分析了主轴质量、滚动导轨副预紧力以及滑块间距对振型分布和固有频率的影响。

1 滚珠丝杠进给系统的功能结构

滚珠丝杠进给系统的功能结构，如图1所示。包含伺服电机、联轴器、丝杠、螺母、导轨、滑块、主轴和承载台等。主轴、螺母、滑块和承载台固定安装在一起，实际工作中，伺服电机通过联轴器带动丝杠转动，再通过滚珠丝杠副实现承载台的进给运动。丝杠的支撑方式为一端固定一端简支，固定端由背对背安装的一对角接触轴承支撑，简支端采用单个深沟球轴承支撑。

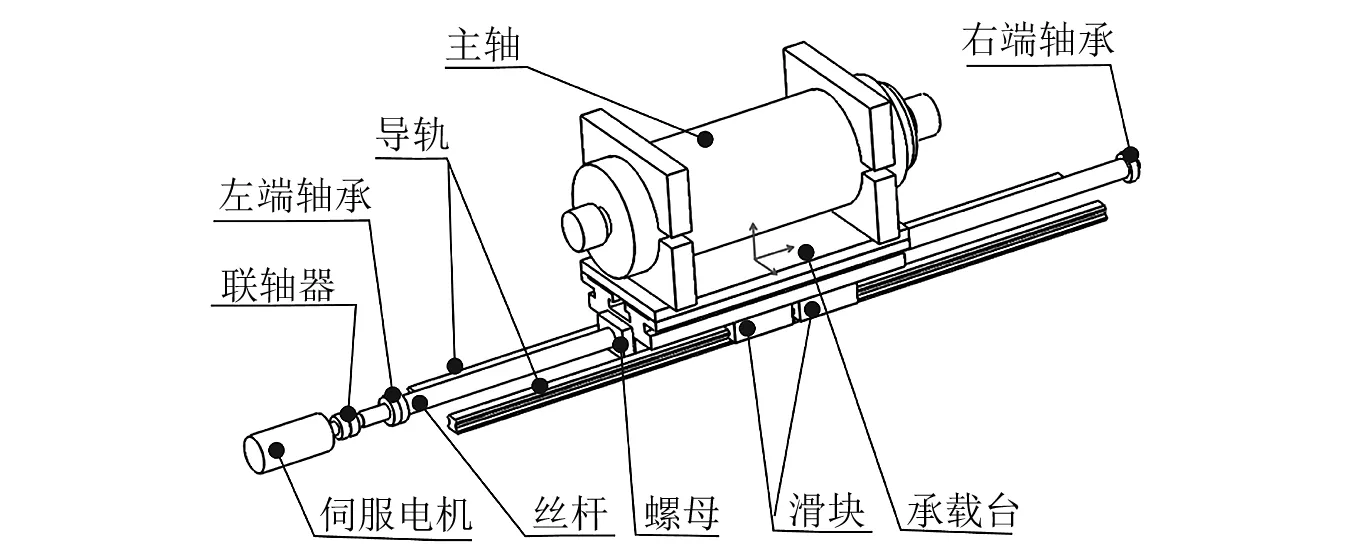
图1 滚珠丝杠进给系统的结构示意图Fig.1 The schematic drawing of the ball screw feed drive

2 结合面的建模与计算

滚珠丝杠进给系统由多个部件通过不同种类的结合面连接而成，依据接触方式的不同，这些结合面可以分为两类:①固定结合面，如主轴、螺母、4个滑块和承载台之间的接触；②滚动结合面，如滚珠丝杠副、滚动导轨副、轴承之间的接触。

2.1 固定结合面

对于固定结合面也需分两种情况讨论：①螺母和承载台，承载台和4个滑块之间的结合面，其刚度较高，为方便计算，在有限元建模时将其作为一个刚体固结在一起；②主轴、支撑板和承载台之间，其结合面的接触刚度相对较低，可能会影响主轴的低阶振动。这里参考文献[16]的研究结论，以螺栓连接处沉头孔的面积区域近似为最大应力区域，以此作为有限元建模的刚性黏结区域。

2.2 滚动结合面

滚动结合面主要存在于滚珠丝杠副、滚动导轨副、轴承等相应部位，其接触形式都是滚珠与滚道的小区域接触。一方面，基于结合面的受力类型和受力方向可将其等效为相应的弹簧-质量模型；另一方面，其小区域接触的特点满足Hertz接触理论的基本条件，Hertz接触理论描述了两物体接触时弹性变形条件下的应力-应变关系，接触模型如图2所示。Hertz接触的基本公式为

(1)

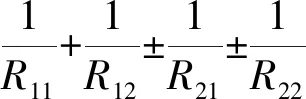
(2)

(3)

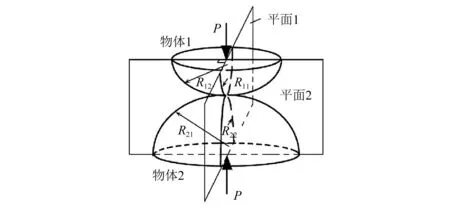
图2 Hertz接触模型Fig.2 The model of Hertz contact

式(1)中：δ为两接触体间的弹性趋近量；Ki，ai为Hertz接触系数，与式(3)中cosτ相关，可通过文献[17]查得；E1,E2为两种接触材料的弹性模量；u1,u2为两种接触材料的泊松比；P为接触法向方向的正压力。式(2)中：Σρ为综合曲率；R11,R12为物体1在两正交平面上的曲率半径；R21，R22为物体2在两正交平面上的曲率半径，当曲面为凹面时，R2i的系数为负。

对以上Hertz接触的基本式(1)求一阶导数可得到滚珠-滚道接触刚度K0的计算公式

(4)

由于滚珠两侧均与滚道接触，所以单个滚珠的等效接触刚度为0.5K0。

2.2.1 滚动导轨副的弹簧质量模型与接触刚度

滚动导轨副的接触模型如图3(a)所示。在预紧力的作用下，滚珠与滚道发生弹性变形，满足Hertz接触理论的基本条件。由文献[18]可获得滚动导轨副的结构参数和材料参数，如表1所示。

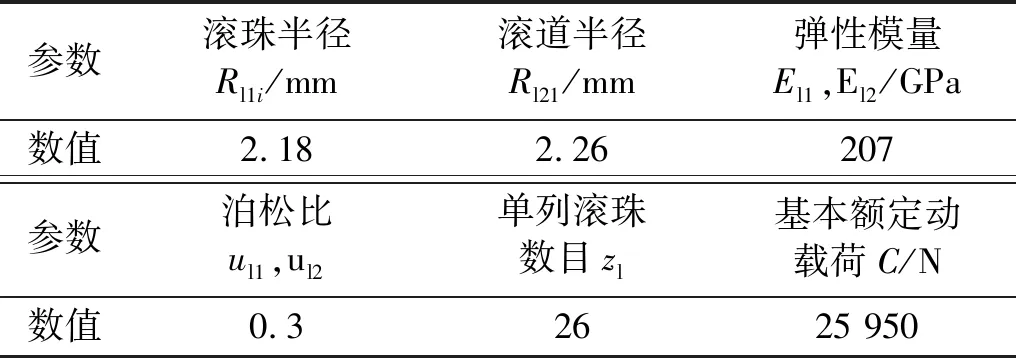
表1 滚动导轨副的结构参数和材料参数

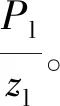
(5)

代入数值求得Kii=2.123×107N/m，滚动导轨副的等效弹簧质量模型如图3(b)所示。

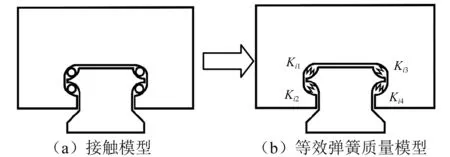
图3 滚动导轨副的弹簧-质量模型Fig.3 The mass-spring model of linear guide

2.2.2 轴承的弹簧质量模型与接触刚度

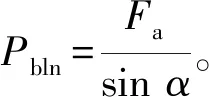
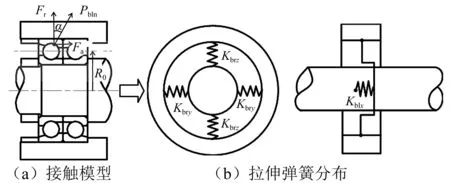
图4 左端轴承的弹簧-质量模型Fig.4 The mass-spring model of left bearing

参数滚珠半径Rb1i/mm滚道圆弧半径Rb21/mm弹性模量Eb1, Eb2/GPa数值2.352.48208参数泊松比ub1, ub2滚珠排列半径Rb0/mm接触角α/(°)数值0.3940参数滚珠数目zb滚道周向半径Rb22/mm数值9Rb0 +Rb1i

1.215×108N

(6)

将左端轴承等效为径向平匀分布的4根拉伸弹簧和轴向的一根拉伸弹簧，如图4(b)所示。则其等效刚度值

(7)

2.2.3 滚珠丝杠副的弹簧质量模型与接触刚度

滚珠丝杠副的受力特点如图5(a)所示。忽略摩擦力的影响，滚珠与丝杠滚道的初始接触点为T1，滚珠与螺母滚道的初始接触点为T2,T1与T2的连线为接触法线n-n。接触法线n-n垂直于丝杠滚道和螺母滚道接触点处的切面M1，M2。若法线压力为Fn1，则其沿轴向、径向和切向的3个分力如图5(b)所示。图中：β为滚珠丝杠副的螺旋角；α为接触角。

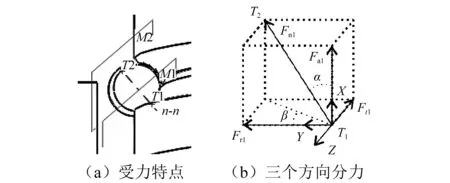
图5 滚珠丝杠副的受力分析Fig.5 The contact-force analysis of screw nut

表3 滚珠丝杠副的结构参数和材料参数

(8)

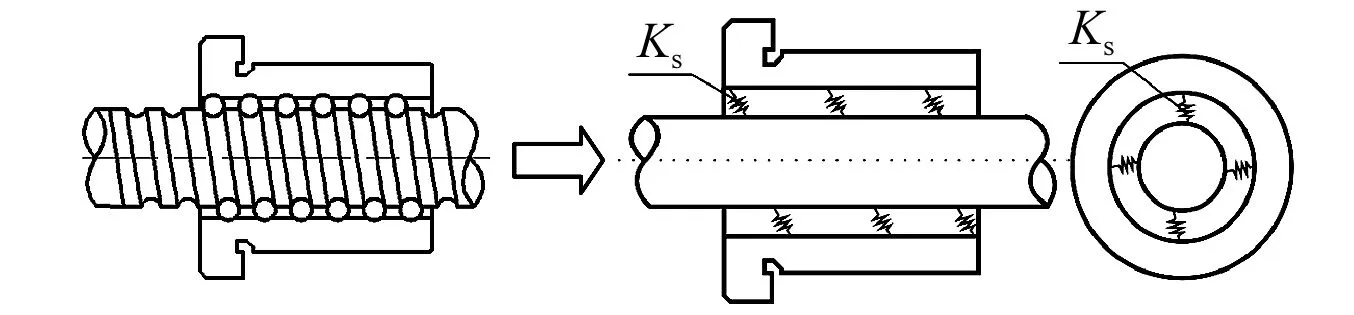
图6 滚珠丝杠副的弹簧-质量模型Fig.6 The mass-spring model of screw nut

3 有限元建模与模态分析

3.1 有限元建模

在三维建模软件中建立如图1所示的实体模型,为方便网格划分，将不重要的小尺寸特征去除，同时将丝杠和各滚动结合面处的滚珠去除，将简化后的三维模型导入ANSYS软件中。在ANSYS中采用不同的单元划分网格，并建立丝杠和各结合面的有限元模型，具体建模方法如下：

①固定结合面，用glue功能将螺母和承载台，承载台和4个滑块黏结在一起；对于主轴、支撑板和承载台的结合面，用glue功能将其螺栓连接处沉头孔的面积区域黏结在一起。

②滚动结合面，依据前文所建立的弹簧质量模型，利用APDL参数化设计语言在各滚动结合面上建立硬点，硬点为弹簧节点与面体单元的结合点；于硬点处建立相应的combine14弹簧单元，依据“2.2”节中的计算结果，定义弹簧的刚度值和拉伸方向。

③除丝杠和滚珠以外的实体部分，采用solid92单元分别划分网格，并赋予各部分所对应的材料属性，如密度、弹性模量、泊松比等。

④丝杠，在ANSYS中，于丝杠位置处绘制直线，于前后轴承接触处、滚珠丝杠接触处定义硬点；采用beam188梁单元划分网格，定义截面属性和材料属性；beam188梁单元的每个节点具有6个自由度，可以仿真丝杠的扭转变形。

⑤边界条件，对两导轨底部、伺服电机底面、轴承外圈表面施加固定约束。

最后共划分网格约 15.3 万个，有限元模型如图7所示。图8为隐藏实体单元后各滚动结合面的弹簧单元。

图7 滚珠丝杠进给系统的有限元模型Fig.7 The finite element (FE) model of the ball screw feed drive

3.2 有限元模态分析

对建立的有限元模型进行模态求解，得到承载台的前五阶模态振型与固有频率，如表4所示。以图1的坐标为参考：第一阶模态为承载台绕Z轴的扭转振动(主轴和承载台一起运动，以下类同)，固有频率为34.7 Hz；第二阶模态为承载台绕Y轴的点头振动和沿X轴的轴向振动的耦合，固有频率为76.7 Hz；第三阶模态为承载台绕X轴的扭转振动，固有频率为136.9 Hz；第四阶模态为承载台沿X轴轴向振动和绕Y轴点头振动的耦合，点头振动较微弱，轴向振动为主，固有频率为181.2 Hz；第五阶为承载台沿Z轴的上下振动，固有频率为243.6 Hz。

图8 隐藏实体单元后的有限元模型Fig.8 The FE model after hiding solid elements

表4 有限元模态分析结果

4 模态试验验证

4.1 定条件下的试验验证

为验证有限元仿真的合理性，对滚珠丝杠进给系统进行了模态试验。应用比利时LMS公司的test lab振动噪声测试系统，在图9所示的试验台上进行锤击试验。承载台置于行程的中间位置，滚动导轨副施加中等预紧力(ZA)。采用锤击激励法，锤击点位于承载台右侧底部的中间位置(图9中T5处)；于承载台的4个角和锤击点附近，分别布置5个加速度传感器；如图9中箭头所示，T2点的传感器为三向传感器，可以测得3个方向的振动信号；T3,T4,T6点的传感器为单向传感器，可以测得沿Z向的振动信号；T5点的传感器可以获得沿X向的振动信号。

图9 模态试验测试装置Fig.9 Modal experimental setup

在T5点锤击后，通过LMS模态测试系统获得到点T2(X向和Z向)、点T3(Z向)、点T4(Z向)、点T6(Z向)和点T5(X向)的FRF(Frequency Response Function)曲线，汇总后如图10所示。图10中，T2Z表示于T2点测得的沿Z向的振动信号，其余类似。

图10 测试点T2,T3,T4,T5,T6处的FRF曲线Fig.10 The FRFs of point T2,T3,T4,T5 and T6

由图10可知，频率为35.1 Hz时，曲线T2X和T5X出现共振峰值，峰值处两曲线的相位相差约180°，符合第一阶振动的固有频率和振型。频率为81.8 Hz时，曲线T2Z和T3Z点出现共振峰值，曲线T4Z和T6Z出现较低的共振峰值，且两组的相位相差约180°，表明承载台在绕Y轴做点头振动；同时，T2X和T5X也出现共振峰值，表明承载台有轴向振动，这与第二阶承载台绕Y轴的点头振动和沿X轴的轴向振动的耦合振动相符；频率为149.1 Hz时，T2点，T3点，T4点和T6点沿Z向出现共振峰值，峰值处T2Z和T4Z的相位一致,T3Z和T6Z的相位一致，且两组的相位相差约180°，同第三阶振动的固有频率和振型相符；频率为166.4 Hz时，曲线T2X和T5X出现共振峰值，且相位一致，同第四阶轴向振动的固有频率和振型相符；频率为231.5 Hz时，点T2，点T3，点T4和点T6沿Z向出现共振峰值，且相位一致，同第五阶上下振动的固有频率和振型相符。固有频率的仿真值和试验值的对比如表5所示。

分析可知，仿真和试验得到的模态振型基本一致，固有频率的最大误差为8.9%，有限元模型的合理性得以验证。

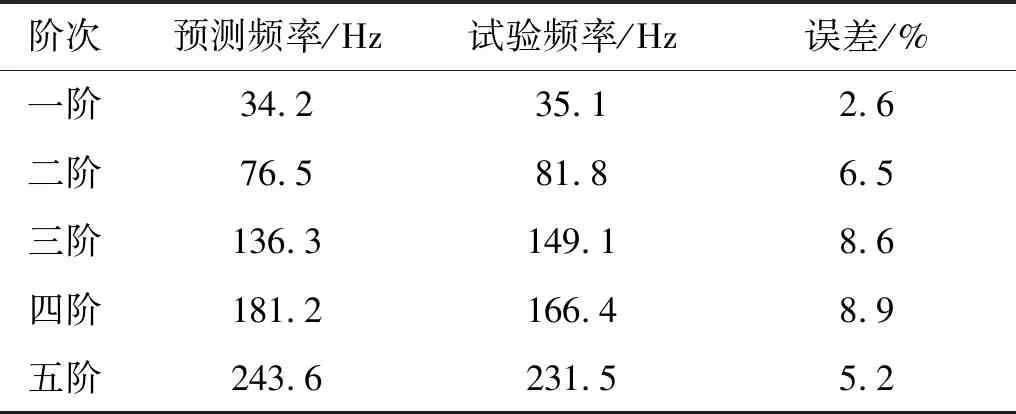
表5 预测频率与试验频率对比

4.2 变条件下的试验验证

为了进一步验证有限元模型的合理性，将承载台置于不同位置，对比不同位置下仿真值和试验值的变化。具体方法为：将承载台的行程均分为5个位置， 于ANSYS中分别计算不同位置下的各阶固有频率；同时，将承载台置于相应位置，分别进行模态试验。

图11为不同位置处，各阶固有频率的试验值和仿真值的变化曲线；表6为不同位置处，仿真频率相对于试验频率的误差。由图11可知，承载台位置发生改变时，仿真值与试验值的变化趋势基本一致；由表6可知，不同位置处，各阶固有频率的最大误差为9.4%；其中，第一阶频率的误差最小，均在3%以内。因此，承载台位置发生改变时，有限元模型的合理性依然可靠。此外，承载台由丝杠固定端移向另一端过程中，第二阶点头振动和第四阶轴向振动均有下降趋势，其余各阶频率基本不变。这是由于第二阶和第四阶的振动特性受丝杠轴向刚度的影响，随着丝杠受拉长度的增长，其固有频率也随之下降，而其余各阶振动并不受此影响。

图11 不同位置下仿真结果与试验结果的对比Fig.11 The simulation results vs experimental results at different locations

误差/%左二左一中间右一右二一阶2.32.02.62.32.6二阶5.76.16.56.55.5三阶8.58.58.68.78.7四阶9.49.18.98.78.6五阶4.74.85.25.15.2

5 动态特性影响因素分析

基于以上验证后的有限元模型，仿真分析以下几个因素对承载台动态特性的影响

5.1 主轴质量的影响

承载台置于行程的中间位置，以主轴原始质量8.99 kg为依据，改变主轴的质量，在ANSYS中分别计算不同质量下的各阶固有频率。固有频率的变化如图12所示。

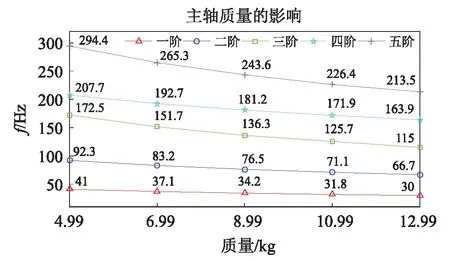
图12 主轴质量的影响Fig.12 The influence of the spindle mass

5.2 滚动导轨副预紧力的影响

承载台置于中间位置，依据“2.2.1”节中的计算方法，针对不同规格的预紧力Z0，ZA，ZB，分别计算滚动导轨副的接触刚度，设定其他参数不变，代入有限元模型中进行仿真计算。

图13为不同预紧力作用下各阶固有频率的变化曲线。由图13可知，随着预紧力由Z0向ZB增大时，各阶频率均有所增大。其中第三阶和第五阶固有频率的增大趋势最显著，第一阶和第二阶固有频率的增大趋势次之，第四阶固有频率的变化最小。这是由于预紧力直接影响导轨滑块的接触刚度，而预紧力越大，刚度值越大，固有频率也越大；其中，导轨滑块主要限制承载台的Z向和Y向位移，第三阶振动和第五阶振动受滚动导轨副Z向刚度值的影响较大，其增大趋势均较显著；第一阶振动主要受滚动导轨副Y向接触刚度的影响，所以也会随之增大；第二阶振动为轴向振动和绕Y轴扭转振动的耦合，而Y轴扭转振动主要受滚动导轨副Z向刚度的影响，所以第二阶固有频率也会随之增大；第四阶振动为承载台以轴向振动为主的耦合振动，基本不受滚动导轨副的影响，所以其变化曲线相对平直。

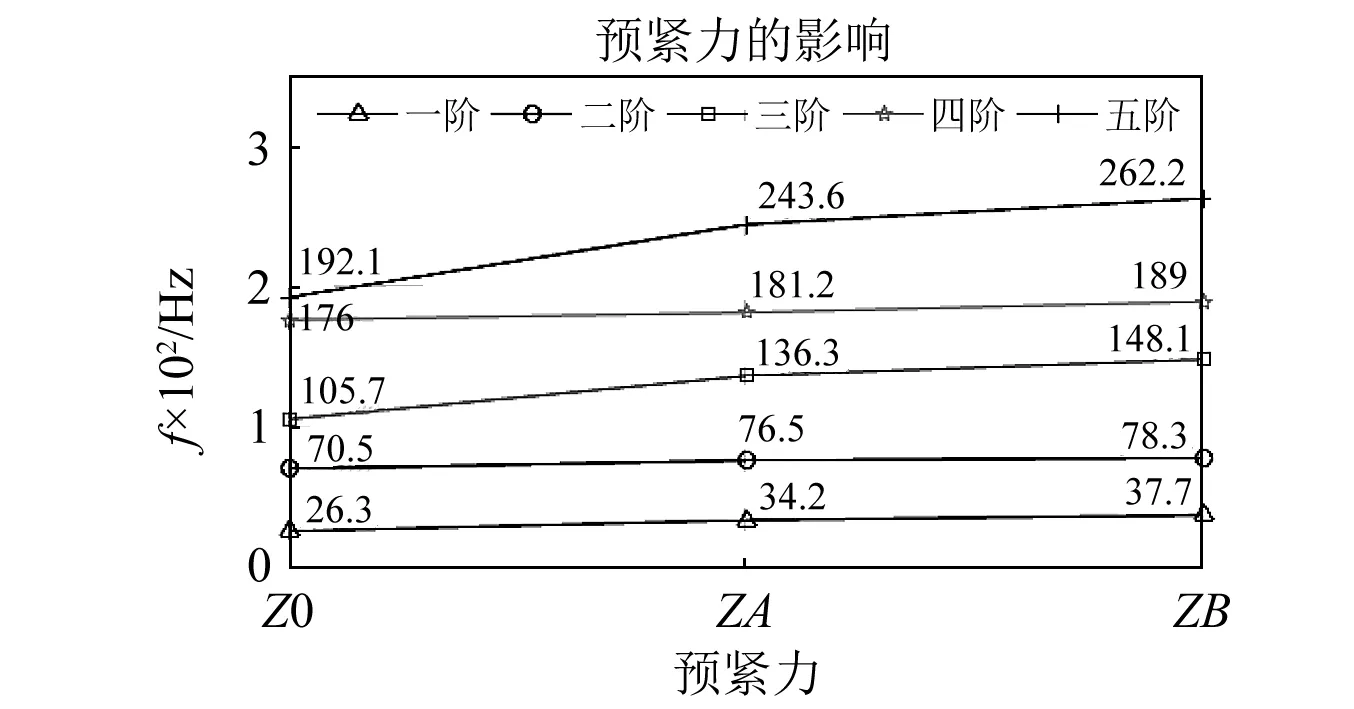
图13 滑块预紧力的影响Fig.13 The influence of the linear-guide preload

5.3 滑块间距的影响

主轴承载台置于中间位置，设置不同滑块间距D，间距D如图14所示。其他参数不变，在ANSYS中分别计算不同间距下的各阶固有频率。各阶固有频率的变化如图15所示。

图14 滑块间距Fig.14 The block interval

图15 滑块间距的影响Fig.15 The influence of the block interval

由图15可知，在滑块间距逐渐增大时，第一阶固有频率和第二阶固有频率都随之增大，而第三阶、第四阶和第五阶的固有频率变化很小。这是由于滑块间距影响承载台绕Z轴的扭转刚度，所以第一阶固有频率会随之增大；同时，滑块间距的增大使得承载台绕Y轴的扭转刚度增大，而第二阶振动为承载台绕Y轴的扭转振动和轴向振动的耦合振动，所以其固有频率也会随之增大。第三阶振动为承载台绕X轴的扭转振动，第四阶振动为承载台以轴向振动为主的耦合振动,第五阶振动为承载台沿Z轴的上下振动，这三阶振动基本不受滑块间距的影响，所以其固有频率的变化很小。

6 结 论

(1)建立滚珠丝杠进给系统各滚动结合面的弹簧-质量模型，基于Hertz接触理论推导得到各滚动结合面接触刚度的计算公式。

(2)采用多单元混合的方法划分网格，建立滚珠丝杠进给系统的有限元模型，该模型考虑了各滚动结合面的接触刚度，仿真了承载台的前五阶模态振型和固有频率。

(3)对滚珠丝杠进给系统进行了模态试验验证，仿真的模态振型与试验结果基本吻合，固有频率最大误差为8.9%；当承载台位置发生改变时仿真结果依然可靠，固有频率最大误差为9.4%。

(4)基于有限元模型，分析了主轴质量、滚动导轨副预紧力以及滑块间距对各阶固有频率的影响，揭示了以上因素对承载台振动变形的影响规律，为滚珠丝杠进给系统的动态特性分析和结构优化提供了参考。