正弦压力信号幅值测量无差算法研究

邰寒松 张大有

(北京航天计量测试技术研究所，北京100076)

1 引言

正弦压力信号广泛应用于计量测试中[1]，北京航天计量测试技术研究所研制了正弦压力源[2]，以该源为基础，通过合理的设计，使标准压力传感器和被校压力传感器同时测量该压力源的压力，比较二者的幅值，可实现被校压力传感器幅值的校准。为了提高幅值测量准确性，本文提出了一种控制采样频率为标准激励信号频率整数倍的算法，可实现幅值的无差运算。

正弦压力校准时，激励信号和响应信号都是正弦信号，任意正弦信号都可以表示为公式(1)

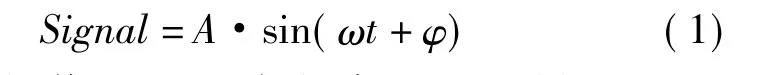
式中：A——幅值；ω——角频率；t——时间；φ——相位。

本文提出的算法，针对式(1)中的幅值处理。

2 常见正弦压力信号处理方法

目前关于正弦信号采样复现的算法已经有一些研究，比如三点法建立在三角函数变换基础上时域中的数据拟合方法，频域方法也称能量矩平衡法通过FFT来实现，布涅曼(Buneman)方法则通过对离散信号进行傅里叶变化然后插值拟合[3]来得出。

工程实践中，数据处理软件上最常用的是通用波形复现法，这是目前正弦压力信号数据处理最常用的方法。该方法的处理步骤如下：

a)在示波坐标系中将每一个采样点表示然后依次连接，以复现波形；

b)取出其中的最大采样值与最小采样值，其差值的一半就作为幅值A；

c)相邻的两个极大采样值之间的时间间隔就作为一个周期T；

d)确定周期以后再利用第一个极大采样值就可以确定相位φ。

以上算法的结果如图1所示，随着采样频率的提高，由信号获得的幅值、相位和周期的准确度都能得到提高，但理论上，误差始终存在。

图1 通用波形复现法示意图Fig.1 General method of reproducing waveform

3 正弦压力信号幅值测量无差算法

校准装置产生的正弦压力源可由公式(2)表征

式中：A0——标准信号源产生的正弦压力的幅值；φ0——标准信号源产生的正弦压力的相位。

传感器的响应信号由公式(3)表征

公式(2)、公式(3)的两个正弦信号中，正弦压力源的幅值A0、相位φ0为已知；传感器响应信号的幅值A、相位φ为未知，两个信号的频率一致，共用ω表示。

在测量传感器响应信号时，按公式(4)控制采样系统频率

式中：fS——系统采样频率；f——标准信号源产生的正弦压力的频率。

根据奈奎斯特采样定理，N的最小值是2，工程上一般要求N最好不小于5～10。本文提出的算法的核心在于：将N严格控制为一个正整数，可以得到严格意义上没有误差的幅值结果。

假设，在t0时刻采样系统第1次进入采样，采到第一个离散值是S1，该值可用公式(5)表征

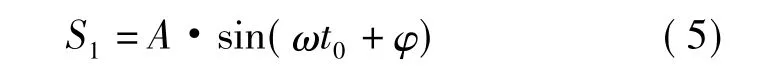
随后的N个连续的采样数据，可以将它们按公式(6)表征

利用三角函数二倍角公式，注意到ω·Ts=ω·并记常数 θ=2ωt0+2φ，整理可得公式(7)

为了得到公式(7)的值，构造一个有N个元素的复数序列{rk}，如公式(8)所示

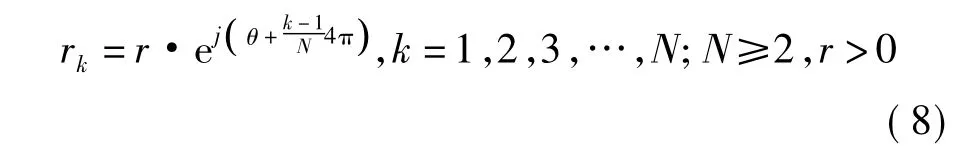
复数具有向量性质。可以在复平面上半径为r的圆上画出这一组复数向量，如图2所示。由于这一个复数序列具有完备的对称性[4]，其对应的向量也具有完备的对称性，所以对于任意大于等于2的正整数N，不论奇偶，公式(9)都成立。

利用欧拉公式ej·a=cosα+j·sinα，将公式(8)写为三角形式可得公式(10)

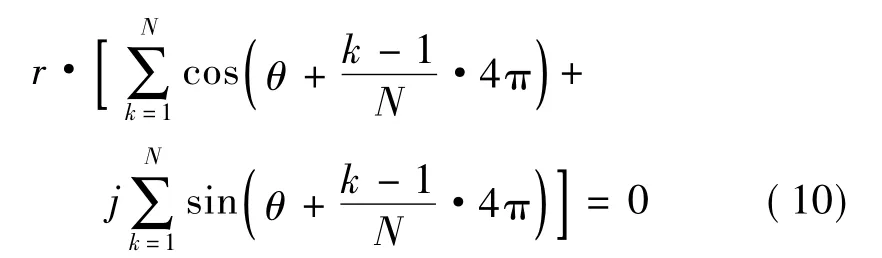
这要求公式(10)表示的复数实部和虚部均为0，故公式(11)成立。

将该结果代回公式(7)，可得公式(12)

对公式(12)求解，可得公式(13)

公式(13)表明，当采样系统的采样频率控制为正弦压力源频率的正整数倍(N倍)时，传感器响应信号的幅值A可通过上式算出，得到的是一个在理论上没有误差的结果。

图2 复数序列的向量表示示意图Fig.2 Vectors of the complex sequence

4 算法的模拟运算

为了验证该算法，利用MATLAB软件进行了模拟运算。按公式(14)模拟产生了正弦信号源。按照本文提出的算法和通用波形复现法分别对该信号源进行了数据采集。

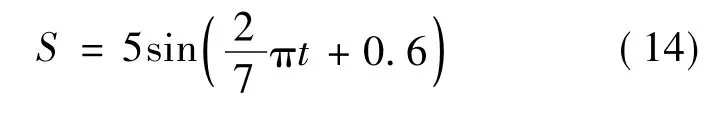
由公式(14)，正弦信号源的频率是1/7Hz，以N=7进行采样，根据软件模拟，依次采样得到的7个点如图3所示，将该数据列表表示，如表1所示。

法国心理学家勒庞认为，人一到群体中就变得低智商、非理性、易盲从，于是他把人群称为“乌合之众”，著有著名的畅销书《乌合之众：大众心理研究》，这本书在国内也备受推崇。勒庞的看法只是一家之言，未见得便是真理，譬如与他同时代的另一位法国心理学家塔尔德便提出了几乎相反的观点。但个体受群体影响，却是没有疑义的。

表1 7个采样点数据列表Tab.1 Data of 7 sampling points

采用通用波形复现法，对数据进行处理的结果如图4，该方法得到的幅值测量值为2A=S2-S6=9.638 048 448，即A=4.819 024 224。

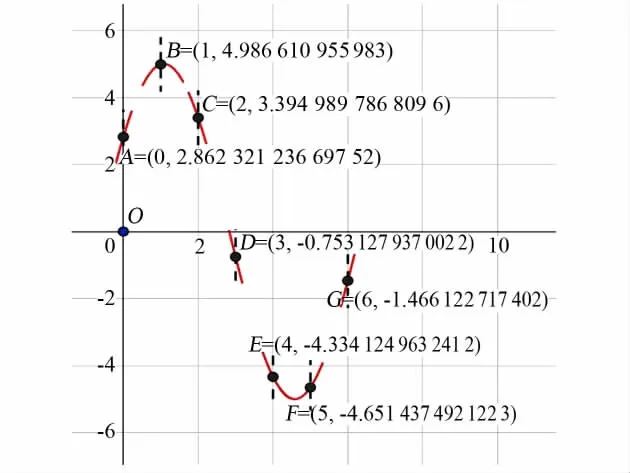
图3 采样数据示意图Fig.3 Data of the sampling points

图4 通用波形复现示意图Fig.4 General method of reproducing waveform

5 算法适用范围

以上讨论中，正弦信号源是单频信号。但在动态压力校准中，除了单频模式，还有扫频信号作为标准激励信号，即扫频校准模式。如果进行扫频校准，标准信号就不再是单频信号，一般地可以表示为公式(15)

若想向类似算法靠拢时，由于信号源的频率发生了改变，就与单频信号有很大区别。

5.1 等间隔采样

可采用与单频标准信号时完全类似的推导过程，唯一区别即信号的频率是一个变化值，但正因此最终无法得出类似的结论。

5.2 变频采样

若使用变频采样，即采样系统的采样频率随标准信号的频率产生变化，如公式(16)所示

式中：fs(t)——系统采样频率随时间变化的函数；f(t)——标准信号源产生的正弦压力的频率随时间变化的函数；ω(t)——标准信号源产生的正弦压力的角频率随时间变化的函数。

一般设定每两个采样点之间的采样间隔取为后一个采样点时刻采样频率的倒数，即公式(17)

若记 ω(tk)=ωk，则在tk时刻满足 ωkTSk=

假设在t0时刻采样系统第1次进入采样，即，采到的第一个值是S1，将一系列采样值记为公式(18)

其中任一项的采样值记为公式(19)。

将公式(19)进一步化简，需要拆分括号内的相乘的部分，将公式(19)的前一项单独列出，记为公式(20)

要让它们之间形成联系，于是就涉及到扫频方式决定的角频率变化规律，分为线性扫频和非线性扫频两种情况进行讨论。

5.2.1 线性扫频

设f(t)=f0+f·t，则在tk-1时刻，ωk-1=ω0+ωtk-1，在tk时刻，ωk=ω0+ωtk，则公式(21) 成立

公式(21)是一个类似数列的迭代关系，不能使得公式(20)的各采样数据之间形成有规律的数学关系。

5.2.2 非线性扫频

非线性扫频的频率变化规律通常为指数或对数，设f(t)=f0·ep·t，则在tk-1时刻，ωk-1=ω0·ep·tk-1，在tk时刻，ωk=ω0·ep·tk，则公式(22) 成立

公式(22)形成了一个迭代关系，不能使得公式(20)的采样数据之间形成有规律的数学关系。

根据以上简单的讨论，对扫频信号，本文提出的算法还不适用。

6 实验验证

在工作平台软件上加入了上面提到的算法。其算法实现局部如图5所示。

在实验中，首先仍然采用Labview自带仿真信号，对3种不同的信号各分别重复实验10次，控制的采样频率与信号频率之间的比值也有所不同。程序前面板如图6所示。

图5 无差算法实现局部Fig.5 Program of the error-free algorithm

图6 无差算法实现前面板Fig.6 Front panel of the error-free algorithm

所得实验数据如表2所示。

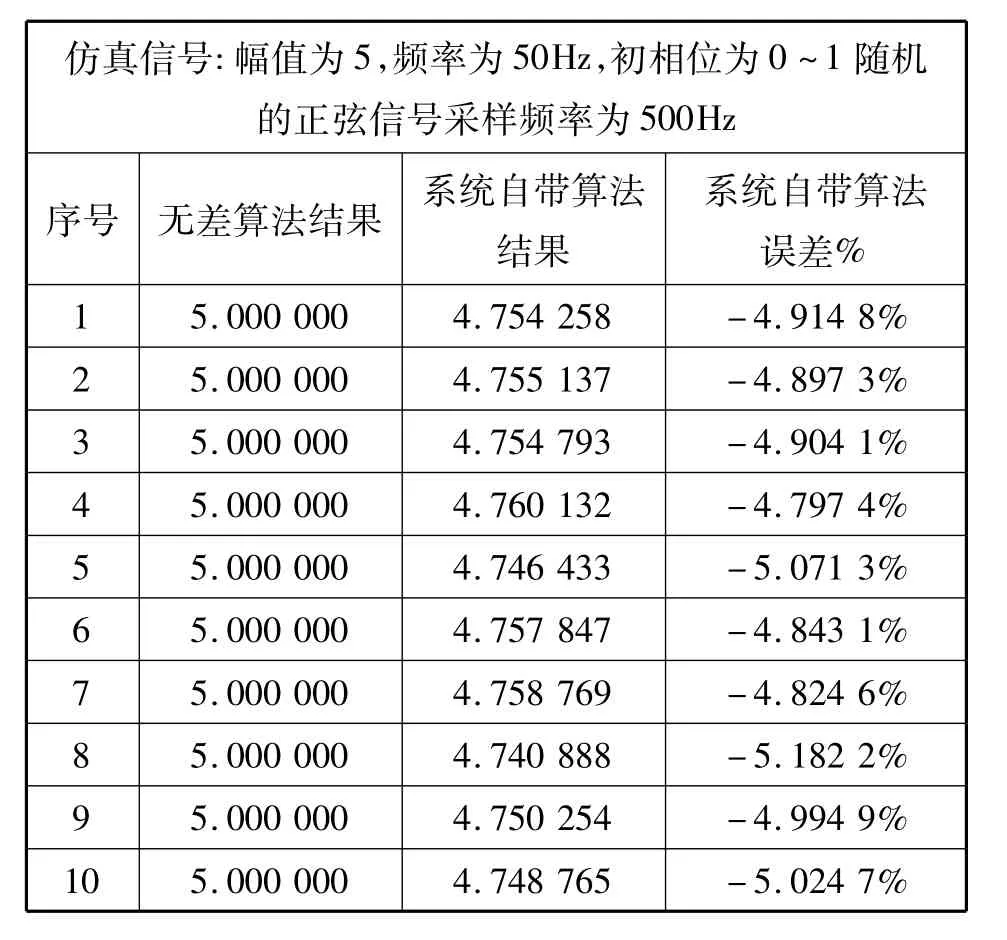
表2 重复仿真实验的数据Tab.2 Simulation experimental data

续表2

对比可知，本文提出的新算法的无差性仍然成立。而目前工作程序所使用的Labview自带的“幅值和电平.vi”程序存在测量误差。这与上面的分析一致。

然后将图5的局部加入工作软件，采用实际信号输入，重做上述实验，同样进行10次，执行数据如表3所示。

表3 工作平台实验数据Tab.3 Data from the work platform

可以看出，实际压力信号由于存在噪声干扰或气源不稳定等因素，新算法的无差性受到了影响。但是对比可知，无差算法有以下改进：

(1)误差更小

利用无差算法的结果由于抹去了算法上的系统误差，仅受系统噪声等干扰，所以其最终的计算误差比起系统自带算法明显减小。

(2)误差稳定性更好

在重复实验中，利用新算法得到结果的误差保持在一个相当小的稳定水准，而且经过大量实验发现这个计算误差受到噪声大小的影响不大；而系统自带算法的测量误差波动较大，并且严重受到噪音大小的影响。这可能是因为根据公式(13)，无差算法的计算公式具有类似均方根的性质，这对噪声的干扰有一个抑制的作用。

综上所述，无差算法的应用可以大幅降低实际校准中幅值测量的误差。

7 结束语

本文提出了一种提高正弦信号幅值测量准确度的新算法，其关键点是通过控制采样频率为激励信号频率的正整数倍，可在理论上实现幅值测量没有误差。

本文提出的算法，目前仅适用单频校准，不适合扫频校准。