格构式塔架顺风向脉动风荷载空间相关性研究

邹良浩 李峰 梁枢果 施天翼 陈寅

摘   要：为了研究格构式塔架顺风向脉动风荷载的空间相关性，选取2段典型的格构式塔架节段模型，采用2个高频测力天平同步测力风洞试验技术，得到了不同水平距离和竖向距离情况下的模型基底剪力和弯矩的风荷载时程. 在此基础上，通过数据处理分析，得到了各工况下塔架的顺风向风荷载相干函数. 试验结果显示：格构式塔架顺风向风荷载相干函数与频率，水平距离和竖向距离等参数有关;结构顺风向风荷载相干函数与顺风向风速以及高层建筑等结构的风荷载相干函数存在一定差别. 最后，采用最小二乘法，拟合得到了格构式塔架顺风向风荷载相干函数经验公式，试验结果与经验公式吻合较好，可为格构式塔架风荷载及风致响应计算提供有用的参考.

关键词：格构式塔架;顺风向脉动风荷载;相干函数;高频测力天平

中图分类号： TU312.1                 文献标志码：A

Abstract： In order to study the spatial correlation of the along-wind fluctuating wind load of lattice tower， two segmental models of a typical lattice tower were selected， and two high frequency force balance technologies were employed. The time histories of the base shear and bending moment for the segmental models considering different horizontal and vertical distances between them were synchronously obtained in the wind tunnel test. Based on the extensive analysis of the obtained data， the coherence function formulas of the along-wind fluctuating wind load on the lattice tower model were obtained. The results show that the coherence functions of the along-wind fluctuating wind load on the lattice tower are related to the frequency， horizontal distance， and vertical distance. There is a certain deviation between the deduced coherence functions obtained by this experiment and the existing coherence functions of longitudinal wind speed or wind load of high-rise buildings. Finally， the least square method was used to fit an empirical formula of the coherence functions of the along-wind fluctuating wind load on the lattice tower. The experimental results are in good agreement with the empirical formula， which can provide a useful reference for the calculation of the wind load and wind-induced response of lattice towers.

Key words： lattice tower;along-wind fluctuating wind load;coherence function;high frequency force balance

隨着现代城市的不断发展，城市建设中对于电力、通讯等的要求越来越高. 格构式塔架结构在电力、通讯和广播电视等领域是不可或缺的结构. 格构式塔架结构是一种具有轻质、高柔和小阻尼特性的特殊结构形式，其结构特征决定其是一种典型的风敏感结构，风荷载为其结构设计的主要水平荷载. 因此，对格构式塔架的风荷载及风致响应的研究尤为必要. 多年来，基于理论分析[1-3]、现场实测[4-6]和风洞试验[7-11]，国内外学者先后进行了格构式塔架的风荷载与风致响应的研究. 现场实测是最直接也是最精确的研究手段，此方法主要以测试结构风速信息与响应信息为主，很难直接得到格构式塔架的风荷载信息[4-5]. 因此，风洞试验方法是进行格构式塔架风荷载研究的主要研究手段. 由于格构式塔架结构特殊性，无法采用测压风洞试验进行结构风荷载测试，因此，高频测力天平（high-frequency force balance，HFFB）风洞试验技术被广泛应用于格构式塔架的风荷载测试中. 梁枢果等[12-13]基于3种典型的格构式塔架HFFB风洞试验，对格构式塔架三维风荷载机理进行了系统研究，并提出了其顺风向一阶振型广义荷载谱解析模型. 然而，HFFB风洞试验技术存在如下缺陷：1）由HFFB技术得到的风荷载为格构式塔架广义风荷载信息，无法得到其风荷载沿高分布的详细信息;2）由高频测力天平得到的格构式塔架广义风荷载为线性振型广义风荷载，该振型与结构实际振型的差别势必带来结构广义力的误差以及由此带来结构响应计算的误差;3）由高频测力天平无法得到结构高阶振型广义力，因而在进行结构风致响应计算时，无法考虑高阶振型的贡献.

针对以上问题，通过假定气动力沿高不变以及一定的相干函数，文献[14]进行了结构风荷载与风致响应的振型修正研究. 在此基础上，文献[15-16]以修正线性振型广义荷载谱方法，进行了结构高阶振型广义力的推导，将HFFB风洞试验技术应用到可考虑高阶振型贡献的结构风致响应计算中. 然而，上述研究往往采用现有的相干函数公式. 已有研究表明，顺风向结构脉动风荷载的相关性要明显大于脉动风速的相关性[17]. 文献[18]通过测压风洞试验方法得到了高层建筑结构顺风向风荷载相干函数，并分析了其与脉动风速相干函数的差别. 考虑到格构式塔架与高层建筑结构形式的差别，其荷载相干函数势必也存在一定差别，因此，研究格构式塔架顺风向脉动风荷载的空间相关性，了解其风荷载的空间分布规律是很有理论意义与实际应用价值的工作.

目前，相干函数拟合公式多以高层建筑[19-21]为研究对象. 不同形式的相干函数计算得到的风荷载及风致响应的相差较大[22]. 基于以上分析，本文选取两段典型的格构式塔架节段，进行两个同步HFFB同步测试风洞试验. 通过调整节段间不同的水平距离和竖向距离，得到各工况下模型的同步风荷载时程. 在此基础上，通过数据处理，分析格构式塔架各节段间的顺风向脉动风荷载空间相关性特性，并分析了其与风速相干函数的差别，最后，建立了格构式塔架荷载相干函数数学模型.

1   风洞试验

1.1   风洞试验设备

本文风洞试验在武汉大学WD-1风洞试验室中进行. 该风洞试验段长×宽×高=16 m×3.2 m×2.1 m，最大风速为30 m/s，试验风速由1 m/s至30 m/s连续可调. 直径2.5 m的自动控制工作转盘可以模拟0°至360°任一风向角的模型试验风场. 试验采用ATI DAQ F/T六分量高频测力天平和NI USB-6218同步采集盒同步测量与采集试验模型的基底剪力与弯矩时程.

1.2   试验模型

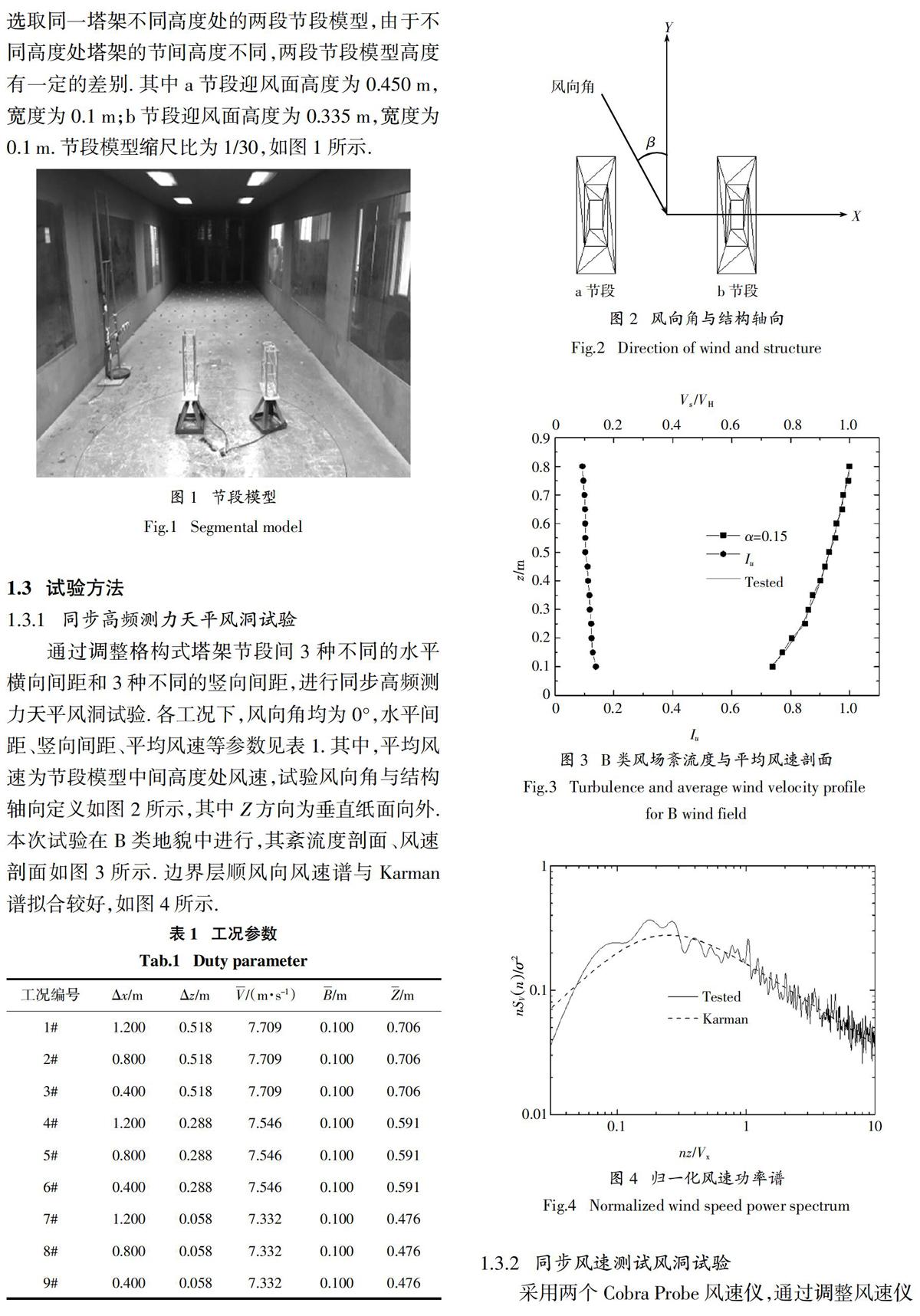
本次试验两个节段模型由某实际圆钢管格构式塔架选取，模型所有杆件由圆钢管制作，杆件间焊接相连，并制作相应升降底座固定模型和调节高度. 为了减小三维绕流效应的影响，节段模型考虑足够的高度以满足杆件较大的长细比[8，23-24]. 考虑到格构式塔架的结构形式随着高度而变化，本次试验选取同一塔架不同高度处的两段节段模型，由于不同高度处塔架的节间高度不同，两段节段模型高度有一定的差别. 其中a节段迎风面高度为0.450 m，宽度为0.1 m;b节段迎风面高度为0.335 m，宽度为0.1 m. 节段模型缩尺比为1/30，如图1所示.

1.3   试验方法

1.3.1   同步高频测力天平风洞试验

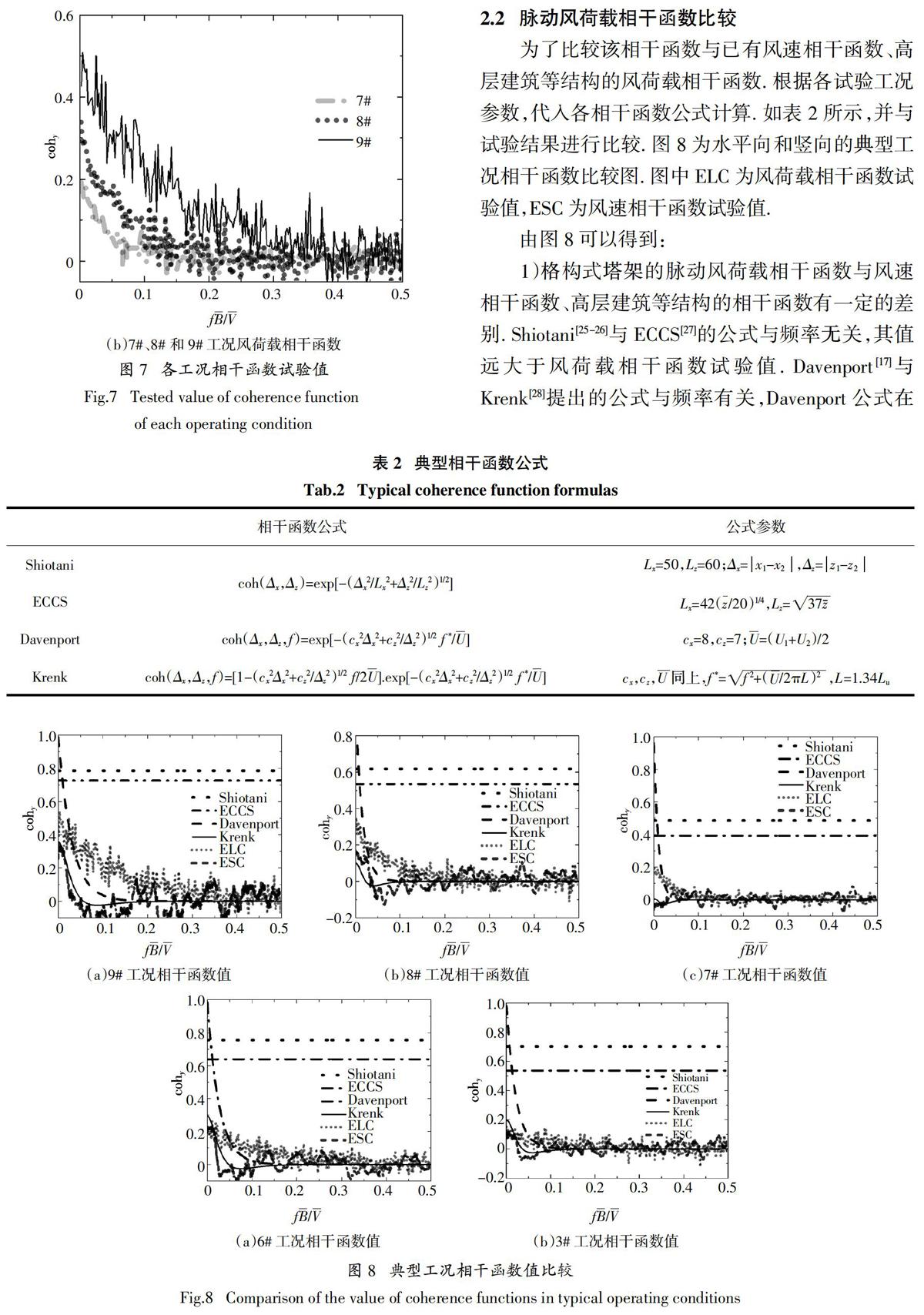
通过调整格构式塔架节段间3种不同的水平横向间距和3种不同的竖向间距，进行同步高频测力天平风洞试验. 各工况下，风向角均为0°，水平间距、竖向间距、平均风速等参数见表1. 其中，平均风速为节段模型中间高度处风速，试验风向角与结构轴向定义如图2所示，其中Z方向为垂直纸面向外. 本次试验在B类地貌中进行，其紊流度剖面、风速剖面如图3所示. 边界层顺风向风速谱与Karman谱拟合较好，如图4所示.

1.3.2   同步风速测试风洞试验

采用两个Cobra Probe风速仪，通过调整风速仪竖向间距、水平间距、试验风速等工况参数，使之与同步高频测力天平试验工况完全相同，进行同步风速测试风洞试验. 同步风速测试风洞试验如图5所示.

2   顺风向脉动风荷载相干函数模型

2.1   脉动风荷载相干函数计算及其特性分析

图7分别为水平距离不变、相干函数随竖向距离减小时的变化和竖向距离不变时，相干函数随水平距离减小时的变化，其横坐标为fB/V，B为节段的平均迎风面宽度，V为两节段中部高度处的平均风速.

由图7分析可以得到脉动风荷载空间相关性的特性：各工况下，相干函数值随折算频率增大，迅速衰减，最后趋于稳定，基本符合指数型衰减规律;在频率接近0时相干函数均小于1;随着水平距离与竖向距离的减小，脉动风荷载相关性均呈增大趋势，在拟合公式时，需要同时考虑脉动风荷载的水平和竖向的相关性.

2.2   脉动风荷载相干函数比较

为了比较该相干函数与已有风速相干函数、高层建筑等结构的风荷载相干函数. 根据各试验工况参数，代入各相干函数公式计算. 如表2所示，并与试验结果进行比较. 图8为水平向和竖向的典型工况相干函数比较图. 图中ELC为风荷载相干函数试验值，ESC为风速相干函数试验值.

由图8可以得到：

1）格构式塔架的脉动风荷载相干函数与风速

相干函数、高层建筑等结构的相干函数有一定的差别. Shiotani[25-26]与ECCS[27]的公式与频率无关，其值远大于风荷载相干函数试验值. Davenport[17]与Krenk[28]提出的公式与频率有关，Davenport公式在折算频率接近0时，相干函数值接近1，大于试验值，随着折算频率增大，Davenport公式迅速衰减，并小于试验值，最后与试验值都趋于0. 而基于Davenport改进的Krenk公式小于Davenport公式值，且无法与格构式塔架风荷载相干函数试验值吻合.

2）风速相干函数试验值小于风荷载相干函数，与Krenk公式值较为接近，符合已有文献相关结论，在另一方面增加了节段模型同步测力天平试验的可信度. 根据比较结果，有必要建立针对格构式塔架脉动风荷载相干函数的拟合公式.

2.3   脉动风荷载相干函数公式拟合

根据顺风向脉动风荷载相干函数特性，考虑采用改进的Davenport指数公式的形式来拟合相干函数，拟合公式形式见式（4）. 首先，运用非线性最小二乘法拟合各个工况的相干函数，得到待定參数c1、c2和c3的值，见表3. 其中，c1为考虑水平距离的衰减参数，c2为考虑竖向距离的衰减参数，c3为与水平距离和竖向距离均有关的衰减参数，随两者增大而减小. 其次，根据各工况参数的离散拟合值，对其进行拟合. 由离散拟合值分析，c1和c2的值基本接近，考虑拟合c1和c2为常数;c3的值随水平和竖向距离的减小而显著增大，考虑以无量纲Δx/B、Δz/Z的指数公式来拟合c3的值. 各参数拟合公式见式（6）（7）. 图9为参数拟合过程. 图10为相干函数拟合公式和试验值部分比较结果，其中ELC为风荷载相干函数试验值，FLC为风荷载相干函数拟合值.

3   結   论

本文通过格构式塔架节段同步高频测力天平风洞试验，得到了各工况下节段的同步风荷载时程，并推导了其相干函数. 分析了脉动风荷载相干函数的变化规律，并与其它的相干函数公式进行比较. 最后建立了相干函数的数学模型，得出以下结论：

1）各工况下，随水平距离与竖向距离减小，格构式塔架顺风向脉动风荷载相关性增大;随折算频率增大而减小，总体上符合指数型衰减公式的规律.

2）现有的顺风向脉动风速相干函数、高层等结构风荷载相干函数与本文得到的格构式塔架顺风向风荷载相干函数均存在一定的差别，如采用现有的风速或其它结构形式的相干函数进行格构式塔架风致响应分析，可能导致较大的误差.

3）根据顺风向脉动风荷载相干函数特性，采用修正的Davenport指数公式的形式拟合相干函数，公式形式较为简洁，且拟合值与试验值较为吻合，对精细化分析格构式塔架顺风向脉动风荷载具有一定的理论意义和参考价值.

4）本文拟合公式参考了其它相干函数公式的变量而拟合得到，对于格构式塔架脉动风荷载相干函数与更多变量的关系还有待进一步研究和验证.

参考文献

[1]    HOLMES J D. Along-wind response of lattice towers-II，Aerodynamic damping and deflections[J]. Engineering Structures，1996， 18（7）：483—488.

[2]    HOLMES J D. Along wind response of lattice towers-III effective  load distributions [J]. Engineering Structures，1996，18（7）：489—494.

[3]   CALOTESCU I，SOLARI G. Alongwind load effects on free-standing lattice towers[J]. Journal of Wind Engineering and Industrial Aerodynamics，2016，155：182—196.

[4]    MOMOMURA Y，MARUKAWA H，OKAMURA T，et al. Full-scale measurements of wind-induced vibration of a transmission line system in a  mountainous area[J]. Journal of Wind Engineering & Industrial Aerodynamics，1997，72（1）：241—252.

[5]    崔磊，何运祥，汪大海. 台风“海鸥”的风场实测与输电塔风振响        应分析[J]. 防灾减灾工程学报，2016，36（6）：965—971.

CUI L，HE Y X，WANG D H. The wind measurement in the typhoon “seagull” and the wind-induced dynamic responses of the transmission tower[J]. Journal of Disaster Prevention and Mitigation  Engineering，2016，36（6）：965—971.（In Chinese）

[6]    沈炼，韩艳，蔡春声，等. 山区峡谷桥址处风场实测与数值模拟研究[J]. 湖南大学学报（自然科学版），2016，43（7）：16—24.

SHEN L，HAN Y，CAI C S，et al. Experiment and numerical simulation for wind field of a long-span suspension bridge located in mountainous canyon[J]. Journal of Hunan University（Natural Sciences），2016，43（7）：16—24.（In Chinese）

[7]    LI Y，LI Z，YAN B，et al. Wind forces on circular steel tubular lattice structures with inclined leg members[J]. Engineering Structures，2017，153：254—263.

[8]    YANG F，DANG H，NIU H，et al. Wind tunnel tests on wind loads acting on an angled steel triangular transmission tower[J]. Journal of Wind Engineering & Industrial Aerodynamics，2016，156：93—103.

[9]   MARTíN P，ELENA V B，LOREDO-SOUZA A M，et al. Experimental study of the effects of dish antennas on the wind loading of telecommunication towers[J]. Journal of Wind Engineering & Industrial Aerodynamics，2016，149：40—47.

[10]  孙远，马人乐，邱旭. 三边形桅杆杆身风荷载特性风洞试验研究[J]. 湖南大学学报（自然科学版），2017，44（1）：39—46.

SUN Y，MA R L，QIU X. Wind tunnel investigation on wind load characteristics of triangular guyed mast[J]. Journal of Hunan University （Natural Sciences），2017，44（1）：39—46.（In Chinese）

[11]  牛华伟，孔凯歌，陈寅，等. 500kV全联合变电构架体型系数风洞试验及风振系数取值分析[J]. 湖南大学学报（自然科学版），2015，42（11）：80—87.

NIU H W，KONG K G，CHEN Y，et al. 500kVwhole combined substation framework shape factor of wind tunnel test and dynamic response factor analysis[J]. Journal of Hunan University（Natural Sciences），2015，42（11）：80—87.（In Chinese）

[12]  ZOU L H，LIANG S G，LI Q S，et al. Investigation of 3-D dynamic wind loads on lattice towers[J]. Wind & Structures an International Journal，2008，11（4）：323—340.

[13]  梁枢果，邹良浩，赵林，等. 格构式塔架动力风荷载解析模型[J]. 同济大学学报（自然科学版），2008，36（2）：166—171.

LIANG S G，ZOU L H，ZHAO L，et al. Analytical model of dynamic wind loads on lattice towers[J]. Journal of Tongji University（Natural Science），2008，36（2）：166—171. （In Chinese）

[14]  HOLMES J D. Mode shape corrections for dynamic response to wind [J]. Engineering Structures，1987，9（3）：210—212.

[15]  邹良浩，梁枢果，熊铁华，等. 格构式塔架顺风向风振响应[J].土木建筑与环境工程，2009，31（3）：42—47.

ZOU L H，LIANG S G，XIONG T H，et al. Wind-induced dynamic responses in along-wind direction for lattice towers[J]. Journal of Civil，Architectural & Environmental Engineering，2009，31（3）：42—47.（In Chinese）

[16]  ZOU L，SHI T，SONG J，et al. Application of the high-frequency base balance technique to tall slender structures considering the effects of higher modes[J]. Engineering Structures，2017，151：1—10.

[17]  DAVENPORT A G. Gust loading factors[J]. Journal of the Structural Division，1967，93（3）：11—34.

[18]  顾明，张建国. 高层建筑顺风向脉动荷载相干性研究[J]. 土木工程学报，2008，41（11）：18—22.

GU M，ZHANG J G. Coherence analysis of along-wind fluctuating loads on high-rise buildings[J]. China Civil Engineering Journal，2008，41（11）：18—22. （In Chinese）

[19]  曾加東，李明水，李少鹏. 矩形高层建筑顺风向脉动风荷载空间相关性[J]. 哈尔滨工业大学学报，2017，49（6）：150—155.

ZENG J D，LI M S，LI S P. Spatial correlation analysis of fluctuating along-wind loads on high-rise buildings with rectangular section[J]. Journal of Harbin Institute of Technology，2017，49（6）：150—155.（In Chinese）

[20]  ZENG J，LI Z，LI M. Coherence of simulated atmospheric boundary-layer turbulence[J]. Fluid Dynamics Research，2017，49（6）： 1—17.

[21]  HUANG D M，ZHU L D，CHEN W，et al. Vertical coherence functions of wind forces and influences on wind-induced responses of a high-rise building with section varying along height[J]. Wind & Structures an International Journal，2015，21（2）：119—158.

[22]  张建胜，武岳，沈世钊. 不同脉动风相干函数对高层建筑风振响应的影响[J]. 振动工程学报，2009，22（2）：117—122.

ZHANG J S，WU Y，SHEN S Z. Wind-induced response of high-rise buildings analyzed by different coherence functions of gust[J]. Journal of Vibration Engineering，2009，22（2）：117—122.（In Chinese）

[23]  謝强，孙启刚，管政. 多分裂导线整体阻力系数风洞试验研究[J]. 电网技术，2013，37（4）：1106—1112.

XIE Q，SUN Q G，GUAN Z. Wind tunnel test on global drag coefficients of multi-bundled conductors[J]. Power System Technology，2013，37（4）： 1106—1112.（In Chinese）

[24]  邓洪洲，张建明，帅群，等.  输电钢管塔体型系数风洞试验研究[J]. 电网技术，2010，34（9）：190—194.

DENG H Z，ZHANG J M，SHUAI Q，et al. Wind- tunnel investigation on pressure coefficient of steel tubular transmission tower[J]. Power System Technology，2010，34（9）：190—194.（In Chinese）

[25]  TAMURA Y，KAWAI H，UEMATSU Y，et al. Wind load and wind-induced response estimations in the recommendations for loads on buildings，AIJ 1993[J]. Engineering Structures，1996，18（6）： 399—411.

[26]  GB 50009—2012 建筑结构荷载规范[S]. 北京：中国建筑工业出版社，2012： 228—229.

GB 50009—2012 Load code for the design of building structures[S]. Beijing：China Architecture & Building Press，2012： 228—229.（In Chinese）

[27]  SFINTESCO D，SOIZE C. ECCS-Recommendations for the calculation of wind effects on buildings and structures[J]. Wind Engineering，1980，2：1319—1325.

[28]  KRENK S. Wind field coherence and dynamic wind forces[M].Berlin：Springer Netherlands，1996：269—278.