步态研究用可调斜坡设计与空间坐标系建立

杨子涵 蒋量 杨辰 王立端 万祥林 曲峰

摘 要：目的：设计搭建一个镶嵌有三维测力台的斜坡平台，对该平台进行可靠性验证，同时提出对应的空间坐标系建立方案，为未来各行业的需求提供理论数据及参考。方法：采用铝型材配合千斤顶搭建斜坡系统，通过在测力台四角设置反光标志点建立虚拟环节让测力台跟随坡角改变，而后通过自然振动频率、压力中心、反光标志点位移、力值误差来检验该系统的可行性及可靠性。结果：斜坡三方向自然振动频率高于人体步行频率，不同条件下（坡角、动静态）压力中心无显著性差异（P>0.05），反光标志点位移无显著性差异（P>0.05），力值测量（P>0.05）无显著性差异。结论：整套系统在测量斜坡步行时足够精确。采用跟踪测力台的方式并将空间坐标系建立在地面上有助于优化测试流程，便于后期计算。该研究结果应用可满足不同环境下对单块或多块测力台空间位置重新分布的要求。

关键词：生物力学;步态分析;斜坡设计;空间坐标系建立

中图分类号：G804.6 文献标识码：A文章编号：1006-2076（2019）03-0084-06

人们对步态的认识从很早开始，至今对步态的研究多基于水平地面环境下。目前人们对步态的研究已不仅限于单纯的水平地面，例如斜坡及台阶就是两个不同于水平的地面环境并产生更为复杂的平衡控制需求[1]，因为坡角的改变将导致重力相对于行走表面方向的改变，这种变化会对步态有显著影响[2]。在自然环境中完全水平的行走路面较少，北美建筑建造标准建议人工斜坡坡角最大为9°[3]，然而许多自然环境与城市环境中的斜坡常常超过这个坡角（>10°），并降低了人的行走意愿[4]，同时在军事训练中也会不可避免地需要克服不同程度的斜坡[5]，因此对于大坡角的斜坡研究也是有必要的[6]。

有研究使用跑台来产生倾斜表面[7-10]，还有人尝试或建议[11-12]改造跑步机并加装测力台来搭造实验环境，但有研究者指出跑步机环境与真实环境的测试结果相比，肌肉激活类型及动力学数据有差异[13]。因此，通过搭建斜坡而进行的步态研究，例如不同的坡角引起步态的变化以及行走策略的改变[14-15]、斜坡与损伤的关系[16-17]、外骨骼矫形器的设计[18-19]以及机器人的斜坡步态仿真[20]等具有更为重要的意义，因此相对于通过跑台来制造斜坡环境来说，采用斜坡步道来研究行走步态则更具有应用性。通过镶嵌有测力台的斜坡进行步态测试是一种常见的斜坡步态实验环境设置方案，目前已有几种在倾斜的步道中镶嵌有测力台的方法已被采用。一种类型的结构是利用固定角度的坡道与一个分离出来的表面部分并在其坡道地板下放置有一个测力台[21];另一种类型的结构是通过在斜坡的表面嵌入测力台，斜坡坡度为固定的[22-23]或可调节[24-26]。上述两种固定角度斜坡共有一个缺点是这些固定的斜坡系统为每个坡度的研究都需要建设一个单独的坡道，可调坡度斜坡允许我们便捷地进行不同斜坡角度的研究，但相对固定的斜坡系统来说，可调斜坡一般都会使其具有潜在的不稳定性。

虽然不同的斜坡系统已经被使用在许多研究当中，但是在可见的文献当中极少提供相应设计局限性，实验方法以及测力台采集数据的精确性讨论，使得重复实验产生了一定的困难。基于上述原因，本研究拟设计搭建一个镶嵌有测力台的可调斜坡系统，对该平台提出详细的搭建过程并进行可靠性验证，并提出相应的测力台空间坐标系建立方法及动力学数据计算方式，为未来各行业的需求提供理论数据及参考。

1 研究方法

1.1 实验斜坡设计

1.1.1 硬件构成

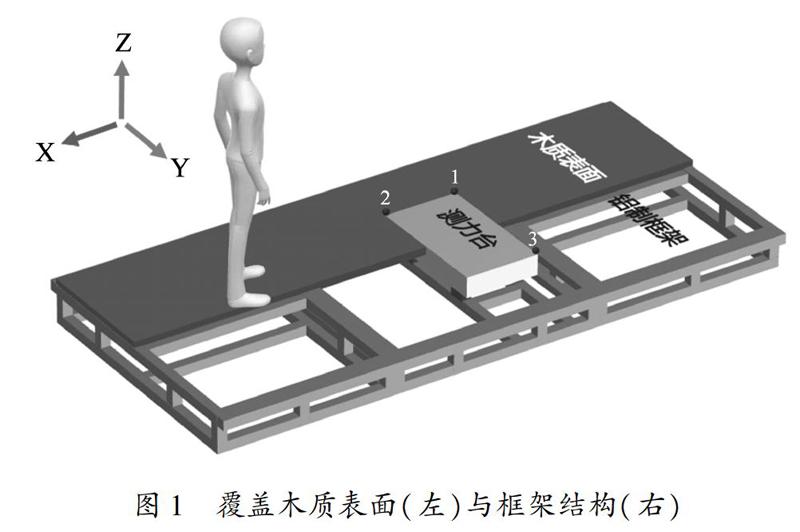
本研究所设计的可调角度斜坡系统（图 1）主要由含有测力台框架的步道与斜坡角度调节装置组成。其中步道由铝制框架以及行走表面组成，铝制框架主体材料由工业铝型材构成，其上安有木质行走表面[14，26]。整个步道长3.16 m，宽1.4 m，高0.21 m，在步道中间的铝制框固定有带螺丝孔铝坯用以安装测力台，并确保测力台四周边缘与木质表面有5 mm间隙。斜坡升起、下降所采用的斜坡角度调节装置是由支撑底板与机械千斤顶两部分组成，支撑底板为钢制，单个千斤顶的理论支撑重量可以达到为1.5～2吨，其最大可升高1.5 m，使得本斜坡系统的坡角范围能够达到±28°。

1.1.2 含有测力台的空间坐标系建立

搭建完的斜坡系统还需要相应的空间标定及测力台设置以便于测试动作的控制及后期動力学数据的计算，因此本研究借助红外光点运动分析系统Motion Analysis（美国）自带的软件（Cortex 2.1.0.1103）当中的“虚拟环节”与“测力台跟随”两种功能来实现。

1）虚拟环节设置

将空间坐标原点设置在水平地面上，在测力台四角放置3个反光点（图 1），接着在所采用的Helen-Hayes人体模型系统中添加三个反光标志点1，2，3以对应。以这三个点建立斜坡系统中测力台的空间坐标系，以点1为原点，求得向量12与向量13，进而求得测力台平面垂直的法向量n，通过已知的法向量n求过点1的一点坐标，在模型编辑中添加一个过点1的虚拟点并将其命名为V_EMR。接着添加一个垂直于平面123的新环节，新环节中的原点为点1，长轴点为V_EMR，平面点为2。

2）测力台跟随设置

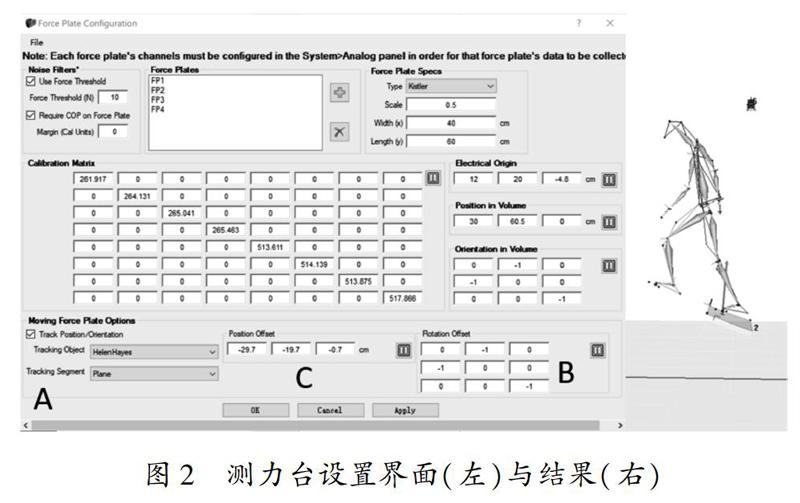
在Cortex程序的测力台相关设置中激活测力台跟随选项（Track Position， 图 2A），其中跟随对象模型设置为本次试验使用的人体模型，进一步选择模型中已设置好的虚拟环节，通过该设置测力台中心将跟随虚拟环节且以点1为中心移动。

3）测力台坐标系转换设置

在Cortex程序的测力台旋转设置中的矩阵描述的是测力台坐标系相对于大地坐标系的方向。空白处测力台坐标系相对于测力台来说是一个方向的余弦矩阵。每一个单元格采用cos（A力台，B标定）来表示测力台A轴与标定B轴之间的角度（Rotation Offset， 图 2B）。通过在设置旋转参数可确保测力台正确显示反作用力方向。

实际应用中还需要根据实际情况通过测力台位置设置输入测力台中心与点1的相对位置来修正（Position Offset， 图 2C），设置好的斜坡环境如图 2右侧所示，通过Cortex软件可以直接进行动力学数据计算。

1.2 斜坡系统测试可靠性检验

本研究从测力台固有频率、压力中心、力值、反光点在测试中的数据精度情况等方面验证斜坡系统测试数据的可靠性[27]。检验所使用的仪器包括一块Kistler测力台（Kistler 9281CA，瑞士），红外光点运动分析系统（Motion Analysis Raptor-4，美国）。其中测力台的采集频率为1 000 Hz，红外光点运动分析系统的采集频率为200 Hz。测试通过两种方式（静态、动态）进行，静态测试是通过测力台采集3秒的安静状态数据，动态测试是指有测试人员（24 a，180 cm，90 kg，）以个人习惯速度（1.2 m/s）在斜坡上上下行走时3秒的数据。

1.2.1 斜坡上三维测力台的固有频率

斜坡步道振动固有频率与人体步行动作频率相近时会对测力台采集到的数据产生干扰。在测试中通过同一个测试人员使用同一橡胶钝器来分别敲击测力台中心与斜坡步道中段，通过比较因为外部力导致安装在地面上和斜坡步道上的测力台产生自身振动的固有频率来验证振动频率是否一致[11]。

首先对安装在地面的测力台进行3次每次持续时间3秒的测试。随后将测力台安装到可调斜坡上，3次敲击测力台，3次敲击斜坡步道。测力台X、Y、Z三方向的频率通过快速傅里叶变换（FFT）进行分析。

1.2.2 斜坡上三维测力台的压力中心误差

为了测试安装在斜坡步道上测力台采集到压力中心数值的精确性，在测力台的上表面标注中心点后（精度为1 mm）贴上十字标志，并用细笔尖对准该中心点施加压力。在对压力中心精度的测试中，在4个角度下（0°、6°、12°、20°）都有静态测试与动态测试。计算静态、动态两种测试条件下每次测试的压力中心坐标（X、Y）的平均值与标准差，并对结果进行双因素重复测量方差分析。

1.2.3 斜坡上三维测力台力值误差

因为测力台的力值输出有可能受到在斜坡上步行所产生的振动影响，测力台力值误差是通过在动态测试与静态测试下已知的静力负荷来验证的，静力负荷通过使用一个重量已知的包胶杠铃片来实现。在0%坡度的时候杠铃片对测力台表面产生了垂直作用力。在斜坡倾斜的时候，杠铃片重力相对斜坡表面产生。输出的力值在静态测试下采集3秒，在动态测试中的力值也采集3秒。测试后对测力台输出力值的平均值、标准差还有变异系数进行比较，并对结果进行双因素重复测量方差分析。

1.2.4 斜坡整体稳定性测试

本研究测力台位置设置是通过反光标志点来实现的，因此需要通过对比粘贴在测力台上的反光标志点坐标在静态和动态之间的差异，分析人在斜坡行走时斜坡的稳定性。应用Motion Analysis红外光点运动分析系统获得反光标志点三维坐标。首先将可调斜坡装置所处的地面作为基准平面（XY平面），采用L型的校准架与T型标定杆进行三维空间标定。一个反光标志点放置于测力台所处模块的靠近千斤顶边缘处。每一个斜坡角度下都采集3秒钟的运动学数据（静态测试、动态测试下），然后计算静态、动态测试各自坐标值的相对误差，并对结果进行双因素重复测量方差分析。

2 结果

2.1 斜坡步道的固有頻率

测力台的固有频率及分别敲击步道及步道上测力台的震动频率如表 1所示。

2.2 三维测力台的压力中心误差

表2双因素方差分析结果表明，压力中心X、Y坐标在不同角度和静、动态之间对比无显著性差异（P>0.05）。

2.3 三维测力台力值

双因素方差分析结果表明，X、Y、Z三方向力值在不同角度和静、动态之间对比无显著性差异（P>0.05）。

2.4 整体稳定性

双因素方差分析结果表明，X、Y、Z三方向坐标在不同角度及动、静态之间对比无显著性的差异（P>0.05）。

3 分析和讨论

对于斜坡研究的空间坐标系设置一般分为两种，一种是在斜面上建立空间坐标系[28]，另一种是在地面上建立空间坐标系。在已知有限的含有动力学测量的斜坡步态研究文献中并没有对斜坡测力台数据在后期的动力学计算过程中的设置方法进行描述[14，21-23，26]，因此其他研究者重复文献中的实验并不容易。

以斜坡平面建立空间坐标系的优点在于可以不需设置测力台参数，缺点在于标定时是以斜坡步道为地面进行标定的，所以关节力矩等需要考虑重力因素重新计算，同时每一个角度下都需要进行角度标定，这样大大增加了工作量。另一套方案则是以实验室地面为测试地面并在其中选择一个已知的点进行空间标定。这样做的优点是测试动作能够正确显示，同时角度调整后并不需要重新标定空间坐标，缺点是考虑到斜坡升起后与地面的距离，其对测试环境中视频捕捉系统的捕捉范围要求比较高。本研究使用第二套方案，通过前文所述的软件设置过程，可以在数据采集界面正确显示测力台，从而减少了测试过程和后期分析动力学特别是关节力矩计算的工作量。目前在理论上能够建立虚拟环节并使测力台跟随环节运动的红外光点运动分析系统都可以通过本方法实现测力台的空间位置重新分布，并进行相应的动力学计算。本研究所采用的空间坐标系标定方法也可进一步应用于其他需要动力学测试的环境，例如台阶步态测试、击打力测试、游泳跳台出发分析等。

测力台固有频率越高，测量时越不易与测试动作共振进而减少误差。本研究所选用的测力台为压电式测力台，固有频率相对于其他应变片测力台较高。压电式测力台的工作原理是由内置的圆柱形传感器的三片切割方向不同的石英分别对X、Y、Z三个方向产生压电效应。因此倾斜测力台会因为重力的原因使测力台本身产生X或Y方向的分力，这个分力类似于在测力台上表面覆盖材料的过程，是可以通过读零来消除的。

研究指出人在步行时至少有99%的地面反作用力小于15 Hz[11，29]，故步行的时候，测力台所采集到的有效数据频率将低于斜坡步道固有频率，这是由斜坡构造和所使用的材料所决定的，因此斜坡的固有频率相对于一般步行来说是足够的。

从表3可以看出本研究中三维测力台力值输出中存在一定的偏差，这是因为Y方向力平均值趋近于0造成变异系数过大导致的，三方向上力值变异性随因斜坡角度变化导致的方向负荷的增大而减小，因此可预期在未来的实验中，相对于测试用的10 kg杠铃片，人行走的数据会有更低的变异性及更好的稳定性。压力中心测试时，各个角度及两种运动方式下压力中心坐标并不绝对为0的原因可能是因为压电式测力台自然噪声的存在，虽然各压力中心最大有0.6 mm的标准差，但不同坡度之间与不同状态下测量值未见显著性差异。这个结果表明在测试中，压力中心始终符合测量的需求。整体稳定性测试结果表明在实验过程中，斜坡有极细微的相对运动（<0.2 mm），这个运动应该是由光学捕捉系统本身的系统误差造成的。同时在多个测试及实验结果当中未发现铝型材结构本身在视频捕捉中产生反光干扰点，因此采用该材料搭建的本系统是可以应用在红外光点运动分析系统环境下的。

图3显示的是10名男性青年（23.7±1.1 a，67.5±5.0 kg，174.8±4.55 cm）以个人习惯速度平地及上坡行走时（0°，6°，12°，20°）的下肢角度（图 3左）力矩（图 3右）时间变化曲线，其中动力学数据采用Butterworth低通滤波法进行平滑，截断频率为15 Hz[30]，该结果趋势与现有文献一致[14，31]。上述关于斜坡系统测试实验的验证结果表明，本设计中的斜坡系统为受试者在斜坡上行走提供了精确的动力学数据。斜坡步道自身的固有频率对于测量反作用力来说是足够准确的。在测试采用的几个坡度中，压力中心输出的数值足够准确，并且测力台输出的受力方向的力值变异性都不高。同时，动态测试相对静态测试来说，人在斜坡步道上行走对测力台采集到的数据没有明显的影响。当人在上面行走时，斜坡步道自身的位移和振动很小。总的来说，安装在斜坡上的测力台并不受到那些干扰条件的影响，依旧能够准确地捕捉作用力的数据。最后，在红外光点运动分析系统下检测到的步道斜坡上粘贴的反光标志点位移在静态测试与动态测试之间的差异几乎可以忽略不计，说明在该斜坡步道系统中可以准确地收集运动学标志（反光标志点）坐标数据。

4 结论

铝型材搭建的斜坡自然振动频率相对人体步行时力值的产生频率是足够精确的，且在红外光捕捉系统中不会产生干扰的反光点。同时压力中心计算精确，力值输出及整体稳定性测试结果有一定波动，但波动处于整体可控范围。采用跟踪测力台的方式并将空间坐标系建立在地面上有助于优化测试流程，便于后期计算，同时本研究结果应用可满足不同环境下对单块或多块测力台空间位置重新分布来进行动力学计算的要求。

参考文献：

[1]Patricia H Honeycutt，Priscilla Ramsey.Factors contributing to falls in elderly men living in the community[J].Geriatric nursing，2002，23（5）：250-257.

[2]A. Goswami. A new gait parameterization technique by means of cyclogram moments： Application to human slope walking[J].Gait Posture， 1998， 8（1）： 15-36.

[3]S. D. Prentice，E. N. Hasler，J. J. Groves，et al. Locomotor adaptations for changes in the slope of the walking surface[J].Gait Posture， 2004， 20（3）： 255-65.

[4]Mark Meeder，Tobias Aebi，Ulrich Weidmann. The influence of slope on walking activity and the pedestrian modal share[J].Transportation Research Procedia， 2017（27）：141-147.

[5]Jiyoung Jeong，Youkeun K Oh，Choongsoo S Shin. Measurement of lower extremity kinematics and kinetics during valley-shaped slope walking[J].International Journal of Precision Engineering and Manufacturing， 2015， 16（13）： 2725-2730.

[6]J. W. Noble，S. D. Prentice. Intersegmental coordination while walking up inclined surfaces：age and ramp angle effects[J].Exp Brain Res， 2008， 189（2）： 249-55.

[7]唐剛，张希安，季文婷，等. 坡面步行中青年女性下肢关节角及肌肉激活度[J].医用生物力学，2011，26（2）：158-162.

[8]A. H. Khandoker，K. Lynch，C. K. Karmakar，et al. Toe clearance and velocity profiles of young and elderly during walking on sloped surfaces[J].J Neuroeng Rehabil， 2010（7）：18.

[9]G. S. Sawicki，D. P. Ferris. Mechanics and energetics of incline walking with robotic ankle exoskeletons[J].J Exp Biol，2009，212（Pt 1）：32-41.

[10]Shani Kimel-Naor，Amihai Gottlieb，Meir Plotnik. The effect of uphill and downhill walking on gait parameters： A self-paced treadmill study[J].Journal of biomechanics， 2017（60）：142-149.

[11]R. Kram，T. M. Griffin，J. M. Donelan， et al. Force treadmill for measuring vertical and horizontal ground reaction forces[J].J Appl Physiol （1985）， 1998， 85（2）：764-769.

[12]A. Belli，P. Bui，A. Berger， et al. A treadmill ergometer for three-dimensional ground reaction forces measurement during walking[J].J Biomech， 2001，34（1）：105-12.

[13]Song Joo Lee，Joseph Hidler. Biomechanics of overground vs. treadmill walking in healthy individuals[J].Journal of applied physiology， 2008， 104（3）：747-755.

[14]A. N. Lay，C. J. Hass，R. J. Gregor. The effects of sloped surfaces on locomotion： a kinematic and kinetic analysis[J].J Biomech， 2006， 39（9）：1621-1628.

[15]E. Al-Yahya，H. Dawes，J. Collett， et al. Gait adaptations to simultaneous cognitive and mechanical constraints[J].Exp Brain Res， 2009， 199（1）：39-48.

[16]Riley C Sheehan，Jinger S Gottschall. At similar angles， slope walking has a greater fall risk than stair walking[J].Applied ergonomics， 2012，43（3）：473-478.

[17]A. K. Silverman，J. M. Wilken，E. H. Sinitski， et al. Whole-body angular momentum in incline and decline walking[J].J Biomech， 2012，45（6）：965-971.

[18]Nathaniel T Pickle，Alena M Grabowski，Jana R Jeffers， et al. The Functional Roles of Muscles， Passive Prostheses， and Powered Prostheses During Sloped Walking in People With a Transtibial Amputation[J].Journal of biomechanical engineering， 2017， 139（11）： 111005.

[19]J. S. Gottschall，T. R. Nichols. Neuromuscular strategies for the transitions between level and hill surfaces during walking[J].Philos Trans R Soc Lond B Biol Sci， 2011， 366（1570）：1565-1579.

[20]Emily Hendrix，Lindsay Hunter，Jesse Dean. Walking Downhill：The Trade-Off Between Energetics And Stability[J].34th anual meeting of American Society of Biomechanics，Providence，Rl，2010：256-257.

[21]M. Kuster，S. Sakurai，G. A. Wood. Kinematic and kinetic comparison of downhill and level walking[J].Clin Biomech （Bristol， Avon）， 1995， 10（2）：79-84.

[22]Hermann Schwameder，Robin Roithner，Erich Muller， et al. Knee joint forces during downhill walking with hiking poles[J].Journal of sports sciences， 1999， 17（12）： 969-978.

[23]BW Stansfield，AC Nicol. Hip joint contact forces in normal subjects and subjects with total hip prostheses： walking and stair and ramp negotiation[J].Clinical Biomechanics， 2002， 17（2）： 130-139.

[24]Edward J McVay，Mark S Redfern. Rampway safety： foot forces as a function of rampway angle[J].American Industrial Hygiene Association， 1994，55（7）：626-634.

[25]Mark S Redfern，James DiPasquale. Biomechanics of descending ramps[J].Gait & Posture， 1997， 6（2）：119-125.

[26]A. S. McIntosh，K. T. Beatty，L. N. Dwan， et al. Gait dynamics on an inclined walkway[J].J Biomech， 2006， 39（13）：2491-502.

[27]A. N. Lay，C. J. Hass，D. W. Smith， et al. Characterization of a system for studying human gait during slope walking[J].J Appl Biomech， 2005， 21（2）：153-66.

[28]K. Kawamura，A. Tokuhiro，H. Takechi. Gait analysis of slope walking： a study on step length， stride width， time factors and deviation in the center of pressure[J].Acta Med Okayama，1991，45（3）：179-84.

[29]Erik K Antonsson，Robert W Mann. The frequency content of gait[J].Journal of biomechanics， 1985，18（1）：39-47.

[30]Shih-Wun Hong，Tsai-Hsueh Leu，Jia-Da Li， et al. Influence of inclination angles on intra-and inter-limb load-sharing during uphill walking[J].Gait & posture， 2014，39（1）：29-34.

[31]Janice J Eng，David A Winter. Kinetic analysis of the lower limbs during walking： what information can be gained from a three-dimensional model？[J].Journal of biomechanics， 1995，28（6）：753-758.