从课本一道习题说数学教学
曾小红
近几年的中考题,题目大多源自课本,从课本习题中寻找命题生长点和拓展点,形成新颖、灵活的中考题。因此,重视课本习题的拓展、探究及应用是具有重要意义的。下面笔者举一例谈谈习题的教学设想。
人教版八年级下册第十九章《一次函数》第109 页13 题:一个有进水管与出水管的容器,从某时刻开始4 min 内只进水不出水,在随后的8 min 内既进水又出水,每分的进水量和出水量是两个常数。容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示。
(1)当0臆x臆4 时,求y 关于x 的函数解析式。
(2)当4约x臆12 时,求y 关于x 的函数解析式。
(3)每分进水、出水各多少升?

本题是分段函数应用题,是课本重点介绍的一种题型,对培养学生的应用意识和推理能力有重要价值。从分析题意可知:本题要考查的知识背景是一次函数、一元一次方程、二元一次方程组,涉及待定系数法求函数解析式、解方程(组)等知识。涉及的数学思想方法有数形结合思想和分类讨论思想。这是一道好题,但教学实践发现,如果讲完或练完本题就此结束此题教学,那么学生在碰到类似问题时依然不会解决,其原因是学生的思维没有得到发展,具体说就是思维的灵活性、深刻性、广阔性、敏捷性没有得到发展,因而学生不能做到举一反三。数学思维培养的载体就是数学问题,抓住数学问题大做文章可以培养和发展思维的品质。为此在全面分析和解决本题之后,笔者主要做了以下变式和拓展。
变式一:变学生熟悉的题材背景,选择与计费有关的问题
题1:某移动公司采用分段计费的方法来计算话费,月通话时间x(分钟)与相应话费y(元)之间的函数图象如图1 所示:
(1)月通话为100 分钟时,应交话费______元;
(2)当x臆100 时,求______与______之间的函数关系式;
(3)月通话为280 分钟时,应交话费______元?

图1
题2:某市电力公司为鼓励市民节约用电,采取按月用电量分段收费办法,若某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线,如图2 所示,根据图象解下列问题:
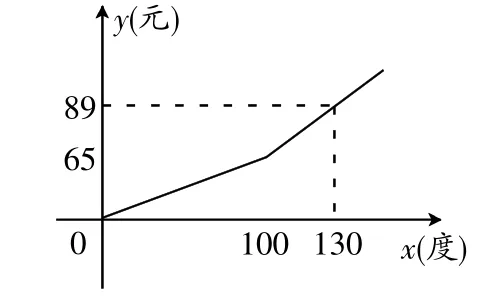
图2
(1)分别写出当0臆x臆100 和x跃100 时,y 与x 的函数关系式;
(2)利用函数关系式,说明电力公司采取的收费标准;
(3)若该用户某月用电62 度,则应缴费多少元?若该用户某月缴费105 元时,则该用户该月用了多少度电?
计费问题涉及面比较广,除了电话费、电费,还可以是水费、出租车收费、销售费用等,这些问题都是学生身边熟悉的问题,对激发学生求知欲和探究欲有很多的促进作用。课标强调从学生已有的生活经验出发,让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程,进而使学生获得对数学理解的同时,在思维能力、情感态度与价值观等多方面得到进步和发展。
变式二:变抽象的题材背景,选择与工程有关的问题
题3:为改造南湖景观,甲、乙两支清淤泥队同时开始清理南湖淤泥,一段时间后,乙队被调往别处,甲队又用了3 小时完成了剩余的清淤任务,已知甲队每小时的清淤量保持不变,乙队每小时清淤50 吨,甲、乙两队在此路段的清淤总量y(吨)与清淤时间x(时)之间的函数图象如图3 所示。

图3
(1)乙队调离时,甲、乙两队已完成的清淤总量为______吨。
(2)求此次任务的清淤总量m。
(3)求乙队调离后y 与x 之间的函数关系式。
课标明确数学在提高人的推理能力、抽象能力、想像力和创造力等方面有着独特的作用,选择此类抽象的问题正是基于此要求。同样的函数图像,稍稍改变数据,还可以把此问题变成与行程有关系的问题。数学是相通的,却又变化万千。相通是因为同一知识点,考查同样的思想方法和能力要求,变化万千是数据可变、题材背景可变。培养学生多数学的爱好就需要教师不断地挖掘学生身边的事例,让学生感觉到数学就在身边,数学可以为生活服务。
以上两个变式都没有改变图像特点,在考查要求不变的基础上,如果变换函数图像,则可以变式的题目更多,甚至可以是多段函数等(本文仅就两段函数举例说明)。
变式三:变函数图像,选择更灵活的题材
题4:据有关资料显示,2017 年底广西农村贫困人口为267 万人,为响应习总书记全面脱贫的号召,实现到2020 年我国现行标准下农村贫困人口脱贫的目标,自治区政府分两阶段实施“精准扶贫”攻坚战,农村贫困人数呈逐渐减少趋势。预计贫困人数与时间变化关系如图4 所示(提示:2017 年底至2020 年底共36 个月)。
请你根据以上材料,结合图像解决以下问题:
(1)当0臆x臆10 时,求y 与x 的函数关系式;
(2) 按照第10 个月后的脱贫变化趋势,请通过计算判断到2020 年底广西能否实现完全脱贫的计划?
(1)在(2)的条件下,若能完全脱贫,请求出在第几个月可以脱贫;若不能完全脱贫,从第21 个月开始月平均脱贫人数至少要增加多少才能保证在2020 年底前完全脱贫?

图4
如何用好教好课本习题,每一位教师都有自己的看法和做法,正所谓“仁者见仁智者见智”。通过习题教学是培养学生的思维和能力的一种有效途径。如何让学生远离题海训练又能培养数学思维、提高解题能力,举一反三,通一而领全局,是每一位数学教师的重要责任。

