GNSS观测数据融合测定地球自转参数精度分析

郭忠臣，凌锦程，姚 翔，李致春

1.宿州学院环境与测绘工程学院，安徽宿州,234000；2.河北工程大学水利水电学院，河北邯郸,056002；3.江苏金地勘测有限公司，江苏南京,210000

地球自转运动可由两部分来描述：地球自转速率的变化和地轴相对于地球的运动[1]，即地球自转参数(Earth Rotation Parameters，ERP)。ERP反映了地球自转的变化，在卫星导航、深空探测等领域有不可替代的作用，是地球参考框架和天球参考框架相互转化的必要参数，也是天文地球动力学领域研究的重要基础数据。实现连续高精度的地球自转参数精确测定，已被列为现代大地测量的主要科学目标之一[2]。为获得高精度的ERP，当前主要使用多种现代空间大地测量技术组合解算，但由于甚长基线干涉测量(Very Long Baseline Interferometry,VLBI)和卫星激光测距(Satellite Laser Ranging,SLR)等技术观测成本较高以及测站不连续等情况，大多情况下仍旧使用全球导航卫星系统(Global Navigation Satellite System，GNSS)观测数据进行解算[3]。魏二虎利用GPS观测数据解算ERP，并将结果与IERS(International Earth Rotation and Reference Systems Service)发布结果进行对比，同时分析当参考站在80个左右时，解算效果较好[4]；姚宜斌等分别对GPS测定ERP精度进行了研究，结果表明,极移解算结果中存在一定的系统误差[5-6]；王新静通过增加新的约束条件，对ERP解算方法进行改进，结果表明,设置先验信息和站点对提高测算精度具有一定的作用[7]；魏二虎对GPS与GLONASS联合测定ERP进行了研究，结果表明,联合测定结果较单GPS具有一定的改善[8]。目前,鲜有学者对BDS和Galileo系统的测定精度进行分析，两系统虽未完全建成，但其观测数据可起到一定的解算作用，对其单独解算以及与其他系统融合解算ERP进行分析，可为后续研究提供一定的参考。

1 GNSS测定ERP原理

GNSS观测方程依据卫星导航系统的基本原理可表示为[9-10]：

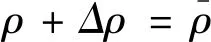
(1)

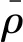
(2)

其中，λ、φ、N分别为载波波长、相位观测值、整周模糊度；dts、dtr、dtrop、diono、dmulti、drel、dε分别为卫星钟差、接收机钟差、对流层误差、电离层误差、多路径误差、相对论误差以及观测噪声的等效距离误差；Xs、Xr分别表示在地固坐标系下卫星和测站的坐标；R表示地固坐标系和惯性坐标系之间相互转换的旋转矩阵，表达式如下：

R=P·N·S·U

(3)

其中，P、N、S、U分别表示岁差、章动、自转和极移旋转矩阵[9]。

对式(1)做线性化处理，可得：

(4)

(5)

其中，R0、S0、U0分别表示地固坐标系到惯性坐标系的旋转矩阵、自转旋转矩阵和极移旋转矩阵。

由此可见，当给定观测时刻及相应的初始地球自转参数值时，即可得到基于GNSS观测数据求解ERP的线性化观测方程，利用迭代最小二乘平差即可求得最终地球自转参数。

2 实验分析

利用GNSS观测数据解算ERP时，不同数量及分布的测站采集的数据对解算结果影响较大，由参考文献[4]可知，选取80个左右大致均匀分布的测站进行解算时，解算效果较好。本文利用75个MGEX测站的观测数据进行研究，分别构造不同实验方案并对结果进行分析比较，所用站点分布见图1。实验采用的计算软件为德国地学研究中心葛茂荣博士提供的高精度GNSS数据处理软件，卫星轨道和ERP初值分别来自广播星历和IERS Bulletin A，测站坐标来自IGS公布的SINEX文件，解算时间为2015/11/16—2015/11/27，年积日为320～331天，每天为一个解算时段。

图1 实验使用的MGEX站点分布图

本次实验主要分两部分进行：(1)由于GPS卫星导航系统已经比较完善，数据质量较高，故单独使用各测站观测到的GPS数据进行解算ERP，并将解算结果与IGS(ftp://cddis.gsfc.nasa.gov/pub/gnss/products)发布的ERP进行对比；(2)使用不同卫星导航系统的观测数据融合解算ERP，分GPS+BDS、GPS+GLONASS、GPS+Galileo、GPS+BDS+GLONASS+Glileo四种方案进行，并将解算结果与IGS发布的ERP进行对比，解算结果见图2(GPS、BDS、GLONASS、Galileo分别简写为G、C、R、E)。

图2 多系统解算结果与IGS差值

对实验结果分析可知：

(1)多系统融合解算ERP时，精度较GPS单系统解算结果无明显提高，甚至会略微下降，这是因为GPS观测数据的质量较其他三系统高，但总体上解算结果的稳定性略有提高。另外，测站的分布情况对解算结果也有一定的影响，构建一套合理、高效的测站选择方案，也是下一步工作的研究方向。

(2)使用四个系统观测数据共同解算ERP时，精度有时反而不如双系统融合或者单GPS系统解算结果，如果定权不当的话，融合后其他系统反而会拉低GPS观测值解算的精度，各系统观测值融合解算ERP时的权值分配也是接下来研究的重点。

(3)多系统融合解算ERP时，可看出极移X方向和Y分量的解算结果与IGS发布的产品存在一定的系统性偏差，日长变化则无明显系统性偏差，主要是因为本文解算策略中所用的天线相位中心、固体潮改正等系统性参数与IGS所用的不一致引起的。

3 结 论

本文通过构造不同实验方案，联合GNSS各系统观测数据测定ERP，并将结果与IGS发布的最终产品进行对比，结果表明：(1)GPS与其他系统观测数据融合测定ERP时，精度较GPS单系统无明显提高，但结果稳定性略有提升，多联合测定的极移X分量和Y分量差值的RMS基本上均小于0.1 mas，日长变化差值的RMS均在0.025～0.032 ms之间；(2)四系统融合测定ERP时，精度有时反不如单GPS或者双系统融合测定精度，这与各系统观测数据质量有关，若定权不当，其他系统反而会拉低GPS观测值的解算精度。

利用GNSS观测数据测定ERP时主要与各系统的可用卫星数及其空间分布有关，BDS的测定精度也低于GPS和GLONASS，为实现我国早日提供各类高精度产品，加快北斗卫星导航系统的建设就显得尤为重要。