C32摩擦焊机液压伺服系统模糊PID控制仿真研究

黄崇莉， 房 舟， 徐永帅， 卫培梁

(1.陕西理工大学 机械工程学院， 陕西 汉中 723000；2.西安理工大学 机械工程学院， 陕西 西安 710048)

摩擦焊接技术是一种高效、优质、节能、无污染的固态焊接技术，随着在航天、航空、石油、船舶等重要领域的广泛应用，生产现场对焊接产品的精度和稳定性提出了更高的要求[1-3]。连续驱动摩擦焊机的控制参数主要包括转速、压力、变形量等，其中摩擦压力是影响焊件性能的主要参数[4]。朱海等[5]通过对摩擦焊机控制系统进行闭环控制设计，提高了系统的可靠性和抗干扰性，但是控制精度达不到所需要求，满足不了高精度的产品要求。钟飞飞等[6]在上述闭环控制的基础上加入PID控制算法，建模仿真结果显示运用PID闭环控制明显提高了轴向压力的控制精度，加快了控制系统的动态性能，但是由于工业现场的许多不确定因素，使得控制过程变得复杂，控制效果达不到理想效果。周春等[7]通过最小二乘法对摩擦焊接压力闭环系统进行模型辨识，并通过离线优化的方法解决了不停产情况下的PID控制参数的整定，保证了焊接产品的质量，但是还是不能实时快速地解决工业现场不确定因素对控制系统的影响。

针对上述问题，本文在传统PID控制算法的基础上引入模糊控制算法，以改善摩擦焊接过程的闭环控制特性，实现对摩擦焊接控制过程的参数自适应调节，以满足控制系统在不确定因素的干扰以及焊接压力突变阶段达到理想的控制效果。

1 液压控制系统组成及数学模型的建立

1.1 液压系统组成及原理

如图1所示，将C32摩擦焊机压力闭环控制系统简化为单活塞杆阀控液压缸伺服系统[8-9]。系统在工作时，首先由工控机给比例换向阀提供一个确定的信号，保证比例换向阀的阀芯在固定位置。然后调定系统的工作压力，压力传感器检测出泵出口压力，经过控制器、放大器的处理，调节比例溢流阀的阀芯位置，从而保证系统的工作压力在外界环境的干扰下仍旧能保持稳定的状态，提高系统焊接的性能。

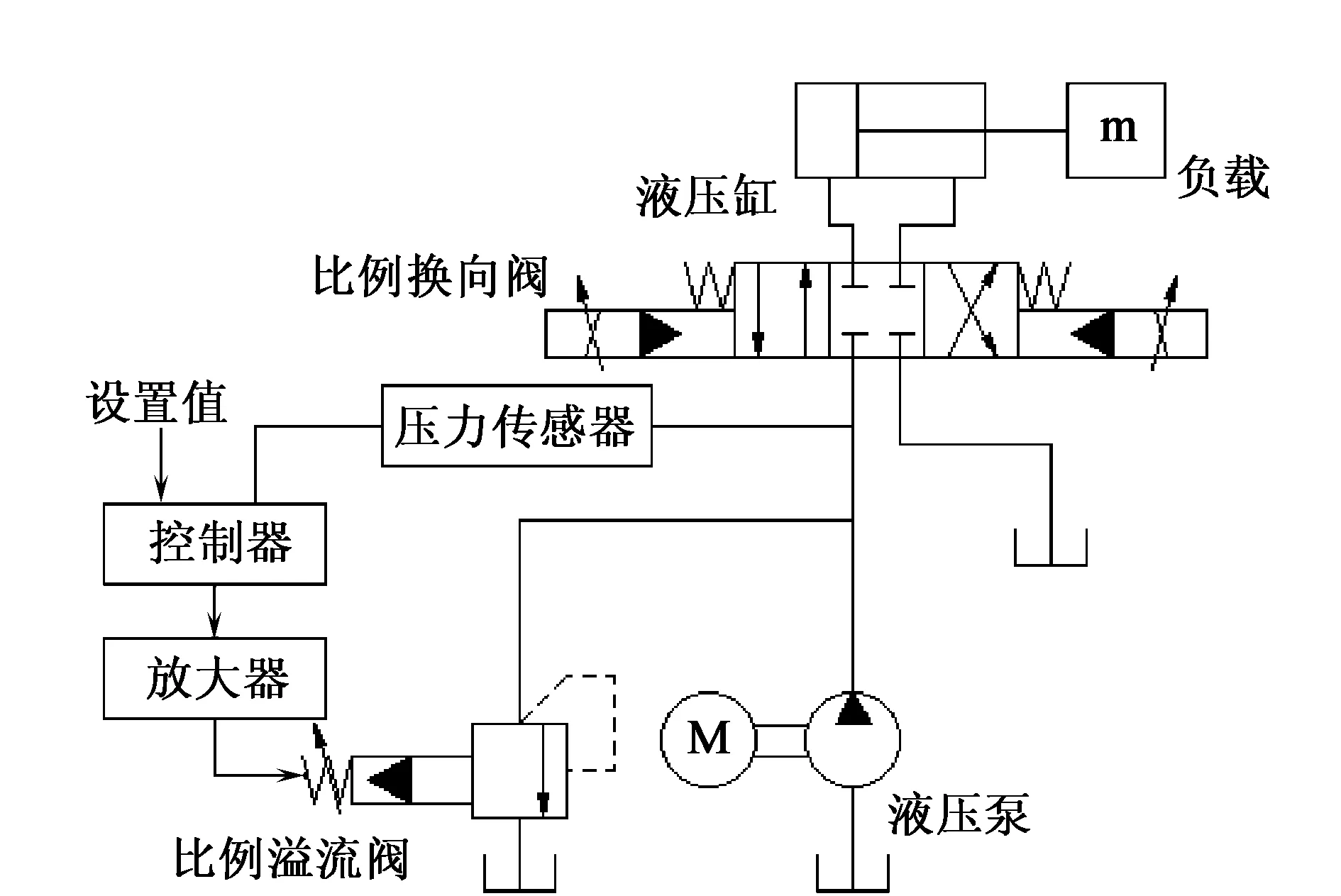
图1 液压系统原理图

1.2 液压控制系统数学模型的建立

C32摩擦焊机液压伺服系统轴向压力闭环控制系统由放大器、比例溢流阀、比例换向阀液阻函数以及压力传感器等组成，控制流程如图2所示。

其压力闭环传递函数为

(1)

其中Ku为比例溢流阀压力增益，G1(s)为比例溢流阀传递函数，G2(s)为比例换向阀液阻传递函数，Kf为压力传感器增益，G4(s)为PID控制器传递函数。具体计算为

(2)

(3)

(4)

(5)

其中PL(s)为比例溢流阀额定压力，U(s)为比例溢流阀的额定电压,ω0为比例溢流阀固有频率，ε0为比例溢流阀阻尼比,R为液阻系数，Vt为液压缸容积，β为有效液体体积弹性系数，cx为液压缸泄露系数,PL1(s)为压力传感器采集的压力值，Uf(s)为将压力值经压力传感器转换采集的电压值。

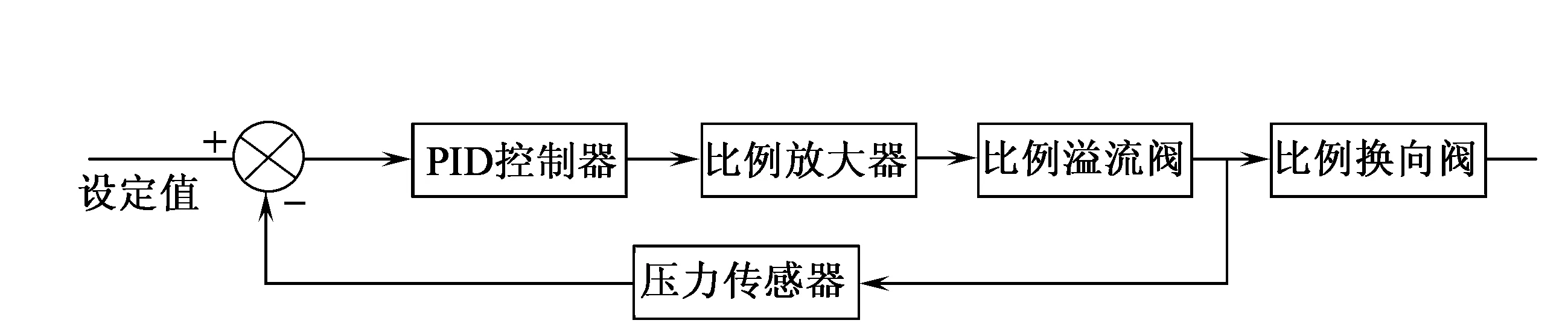
图2 控制系统控制流程图

2 模糊自整定PID控制器设计

2.1 模糊控制器原理

模糊控制是建立在人工经验基础上的一种自适应智能控制算法[10-12]，它是在常规PID控制器的基础上将偏差e和偏差变化率ec作为模糊控制过程的输入量，利用建立的模糊规则对PID参数进行自适应整定，使得控制系统在复杂工业环境下的鲁棒性达到比较理想的状况。其控制原理如图3所示。

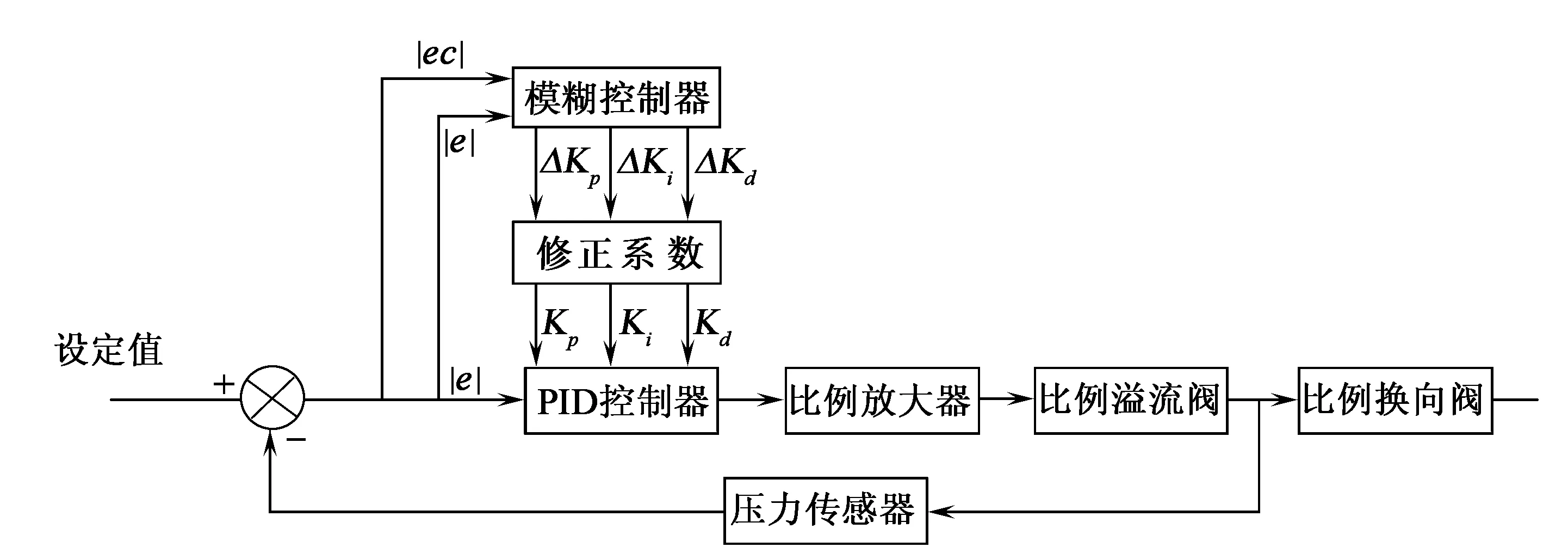
图3 模糊控制器原理

2.2 模糊PID控制器设计

2.2.1 模糊控制器结构设计

根据实际工作要求，确定模糊PID控制器为一个二输入三输出的结构[13]。以偏差e和偏差变化率ec作为控制器的两个输入，ΔKp、ΔKi、ΔKd作为控制器的3个输出。

其中误差e和ec的基本论域为[-10，10]，ΔKp的基本论域为[-7，7]，ΔKi的基本论域为[-8，8]，ΔKd的基本论域为[-0.01，0.01]。e和ec的模糊论域设置为[-3，3]，ΔKp的模糊论域设置为[-1，1]，ΔKi的模糊论域设置为[-0.1，0.1]，ΔKd的模糊论域设置为[-0.01，0.01]。于是，e和ec的量化因子都为3/10=0.3，ΔKp的比例因子为7/1=7，ΔKi的比例因子为8/0.1=80，ΔKd的比例因子为0.01/0.01=1。控制器的模糊隶属函数都选择为三角形，下面只列出e、ec的隶属函数图，见图4。

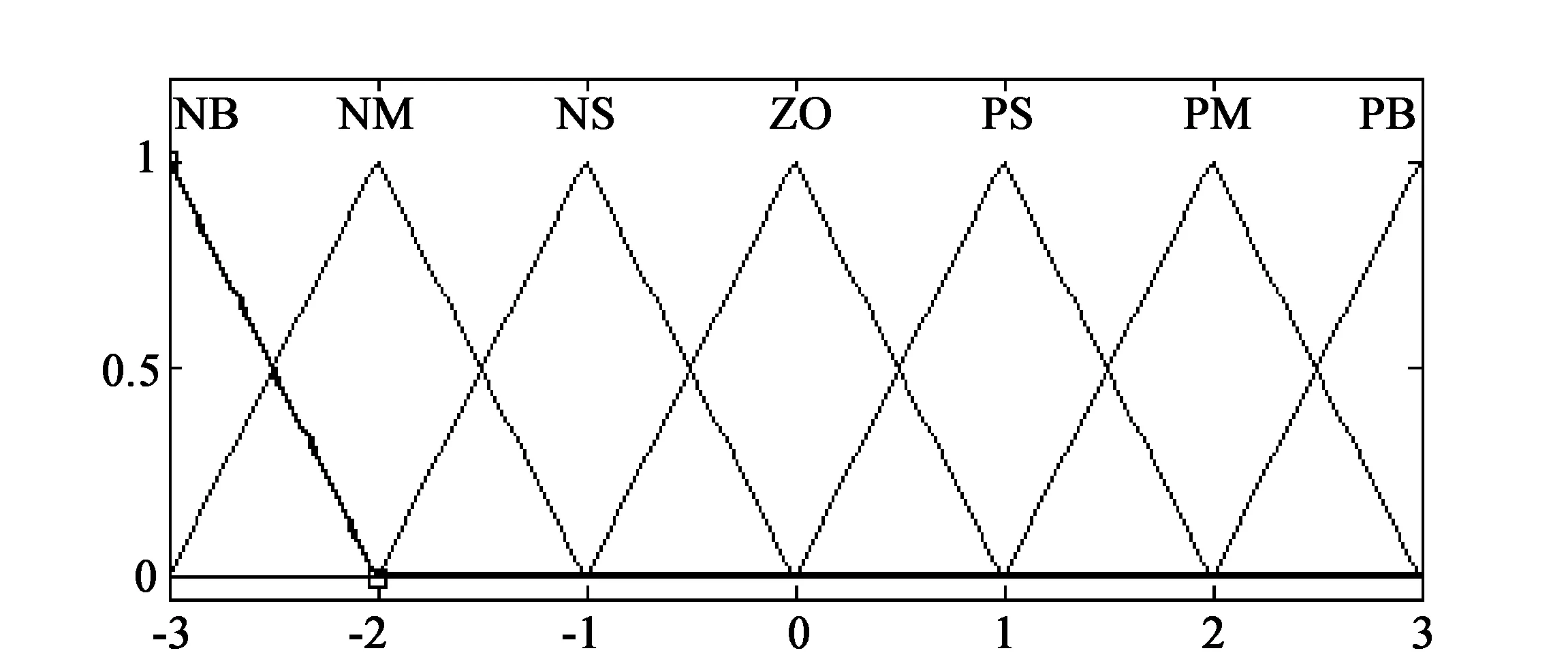
图4 e、ec的隶属函数

2.2.2 模糊规则制定

模糊控制规则的合理建立将直接影响模糊控制的性能。将输入和输出变量的模糊子集都设置为7级，即e、ec、Kp、Ki、Kd={NB，NM，NS，ZO，PS，PM，PB}，其对应模糊子集的语言变量为{负大，负中，负小，零，正小，正中，正大}。根据对液压闭环控制系统的要求和常规PID参数对系统性能的影响，制定如下模糊控制原则：

当偏差e变化较大时，为了加快控制系统的响应速度，忽略ec对系统的影响，对Kp取较大值，Kd取较小值；同时为了避免控制系统超调过大，取一个较小的Ki值。

当偏差e处于中等程度时，为了减小系统的超调，同时又能保证系统的响应速度，Kp取较小值，Ki和Kd取一个适中值。其中Kd取值的大小对系统影响较大。

当偏差e较小时，为了保证控制系统有较好的稳态性能，同时避免控制系统在稳态值出现波动，保证系统的鲁棒性，Kp和Ki取值大一点，Kd取值根据ec大小进行判断，ec大则Kd取小值，ec小则Kd取大值。

根据上述原则，制定控制系统模糊规则如表1所示。

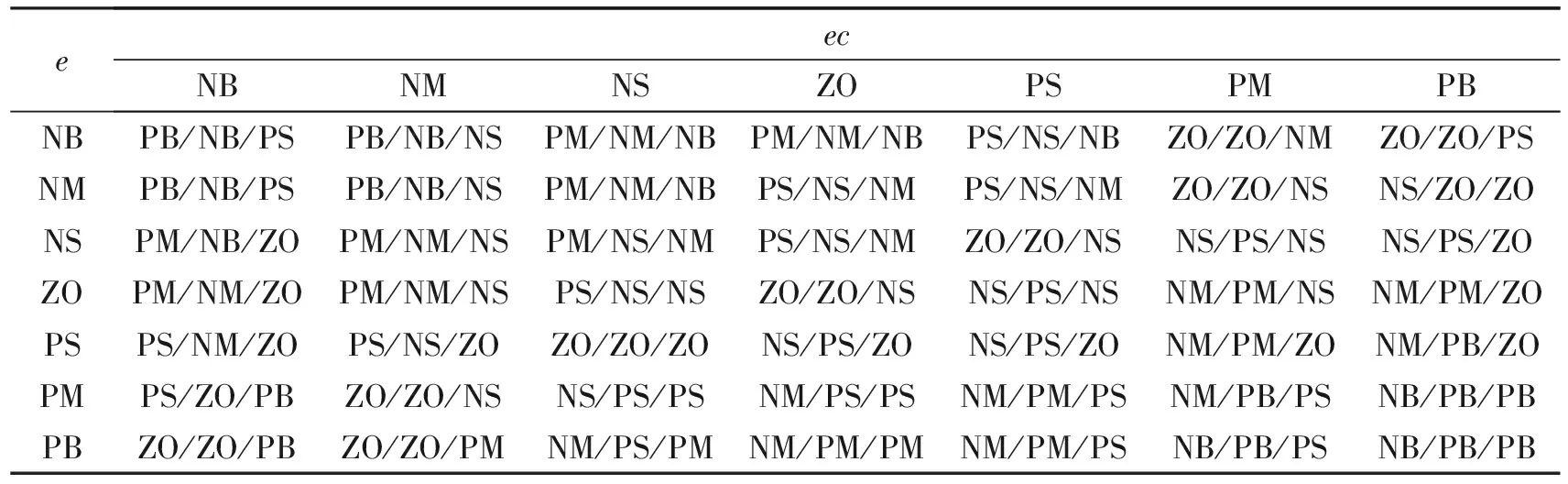
表1 ΔKp、ΔKi、ΔKd模糊控制规则表

2.2.3 模糊控制器求解

运用Mandani推理[14]对模糊PID控制器进行求解，根据每个模糊子集的隶属度范围结合每个参数的模糊控制模型推理出修正参数矩阵表，然后代入下式实时输出修正后的PID参数：

(6)

(7)

(8)

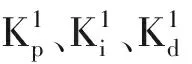
2.2.4PID初值整定

PID参数整定的方法有很多，如衰减曲线法、临界比例法、试凑法等[15]，在工程中一般使用的都是试凑法。其具体过程如下：

(1)控制系统只在Kp作用下调节其值由大到小变化，当曲线出现震荡并且过渡过程为4∶1时，记录下此时的Kp值；

(2)将上一步调节的Kp值减小10%～20%，并加入Ki，调节Ki由大到小变化，直至控制系统静态误差最小为止；

(3)控制系统同时加入Kp、Ki、Kd，在调节Kd值之前，为了弥补微分环节对系统带来的影响，将Kp适当增大，最后调节Kd直至系统达到最佳状态。

经过上述方法对PID参数进行整定，得到PID控制参数的初始值为Kp=0.4，Ki=50，Kd=0.01。

3 仿真研究

在MATLAB2014a的GUI界面中建立e、ec、ΔKp、ΔKi、ΔKd的隶属函数，并通过规则库输入上述控制系统建立的模糊规则，得到ΔKp、ΔKi、ΔKd的逻辑关系曲面图如图5所示。

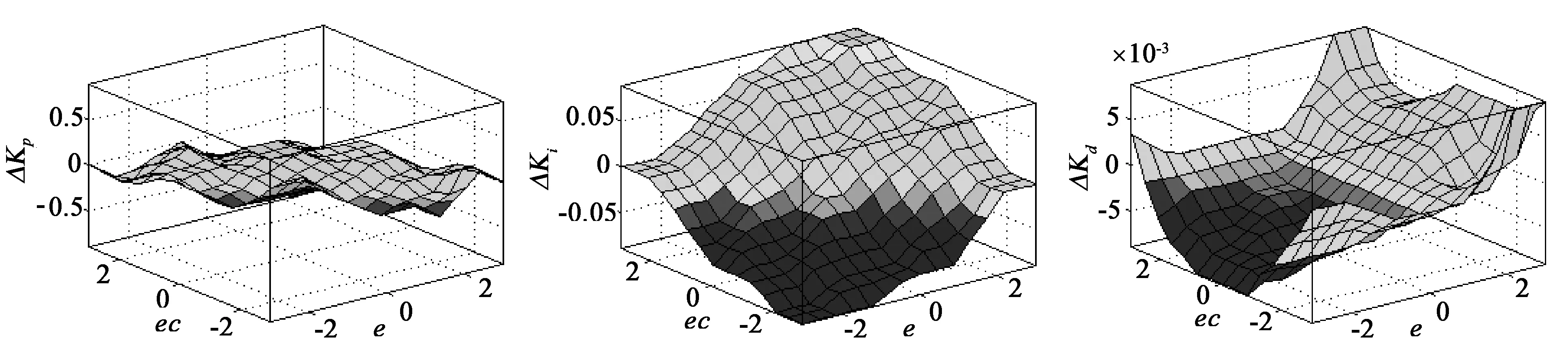
(a)ΔKp (b)ΔKi (c)ΔKd 图5 ΔKp、ΔKi、ΔKd逻辑关系曲面图

根据以上建立的控制系统，在MATLAB的Simulink仿真环境中对其建立如图6所示仿真模型。模型由激励信号、控制器、液压系统各个元件的数学模型等组成。其中模糊PID是由模糊控制器和PID控制器打包组成，如图7和图8所示。在C32摩擦焊机液压系统施加一个幅值大小为1的阶跃信号，观察压力信号在PID作用下和模糊PID作用下的响应情况如图9所示。

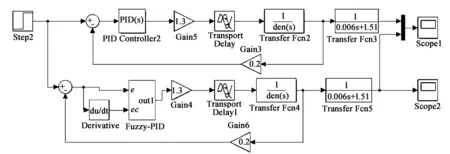
图6 控制系统仿真模型

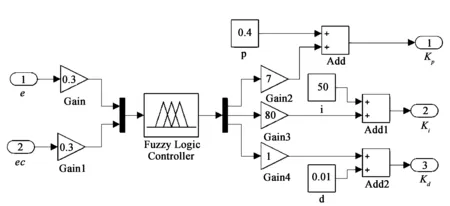
图7 模糊PID控制器图

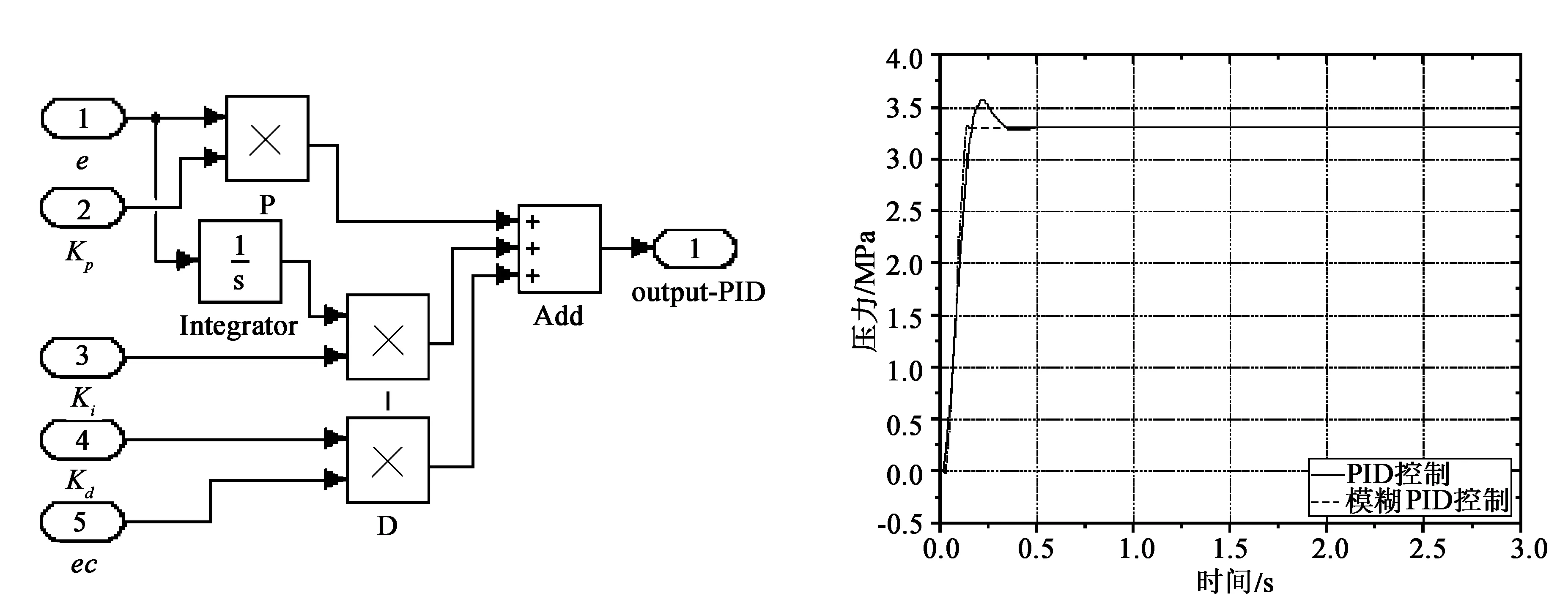
图8 PID控制器 图9 压力阶跃响应仿真曲线图

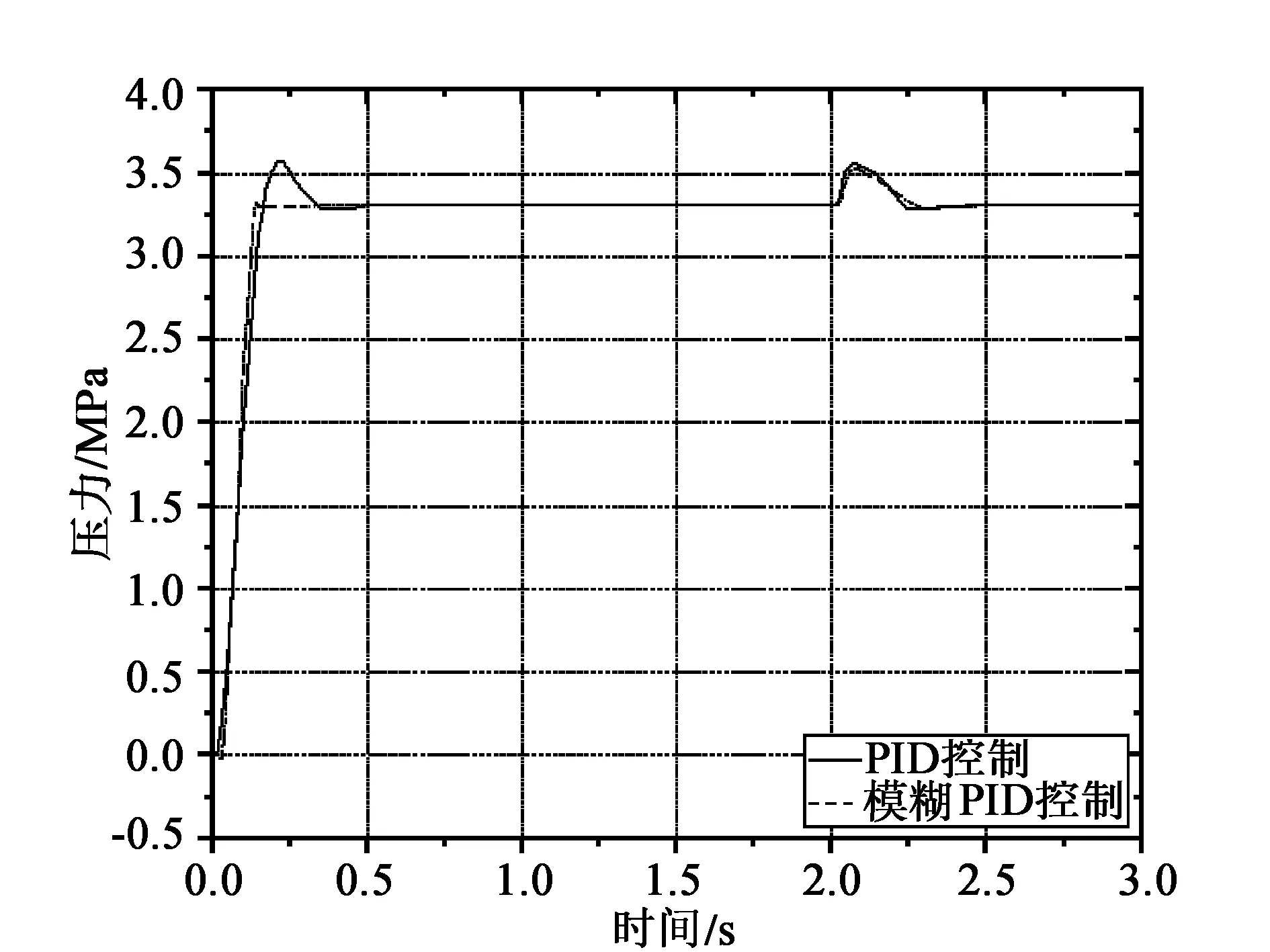
图10 加入干扰后的仿真曲线

如图9所示，曲线1是PID控制下的压力阶跃响应曲线，曲线2为模糊PID控制下的压力阶跃响应曲线。从图中可以看出，摩擦焊机在PID作用下的上升时间为0.15 s，超调量为0.065，调节时间为0.055 s，经模糊PID作用下上升时间减小了0.7%，超调量降低了4%，调节时间减小了5%，这对一个高精度的设备来讲，这些性能的降低有相当大的意义。从上面分析中我们可以得到，相比较PID控制器，模糊PID更能加快系统的稳定性，提高系统的响应时间。

在给系统加入干扰，仿真结果如图10所示。从图中可以看到加入干扰后，PID控制下的曲线在干扰处具有一定的波动，模糊PID控制下的波动更小。

从上述分析中可以得到，模糊PID控制系统的综合性能比PID控制更优，使得液压系统在焊接压力突变阶段达到更理想的控制效果，更能满足生产现场对于产品精度和稳定性的要求。

4 结 论

通过仿真对比分析可知，本文设计的模糊PID控制器可根据系统运行状况对PID参数进行自整定，能够很好地降低工业环境中不确定因素对控制系统的影响，并且在更好地保证控制系统的稳定性的前提下，加快系统的响应速度，减小系统的调节时间，为提高C32摩擦焊机液压控制系统的性能提供了有益的经验。