遗传算法与模拟退火算法在FMS中的混合应用
王 涛,吴林彦,张如伟,王 琪,裴 翦
(1.山东建筑大学,济南 250100;2.山推工程机械股份有限公司,济宁 272023)
0 引言
FMS中的机器装载问题为通过满足技术约束(如可用机器时间和工具槽约束)来分配机器、所选作业的操作以及执行这些操作所需的工具,以确保系统不平衡性的最小化和吞吐量的最大化,同时求解目标函数,使结果更接近FMS环境的真实假设[1]。目前有许多针对FMS中的机器负载问题的研究,并提出了启发式算法来优化系统的不平衡和吞吐量。然而到目前为止,探讨的都是单一的算法而混合算法并没有被广泛应用于FMS问题中。因此针对柔性制造系统中的机器装载问题,提出了一种结合GA和SA的高效混合进化启发式算法,并进行了验证。
1 研究背景
本文所考虑的柔性制造系统是由一些多功能的数控机床和其他能够执行多种操作的设施组成。制造系统中的作业工序是批量可用的,同时每道子工序在加工过程中可以以随机顺序进行排列。当我们已知批次大小、操作次数、加工时间和每个作业所需的刀具槽数,假设有一套工具和一套机器可以生产我们所需的各种各样零件。同时假设加工时间和刀具槽随着分配给不同机器的工件变化而变化,那么就会出现有时某个工具槽工件短缺的情况。对于工件操作来说,通常分为两种:
1)必选操作-此操作只能在特定的机器上进行。
2)可选操作-此操作可以在具有相同或相似加工时间和刀具槽的多台机器上执行。
因此工序中的可选操作使得整个工作流程具有弹性的可能。本文所考虑的FMS具有四个多功能机器,每个机器具有480min的可用处理时间(8HRS=1个移位)和5个工具槽。本文中符号的含义如表1所示。
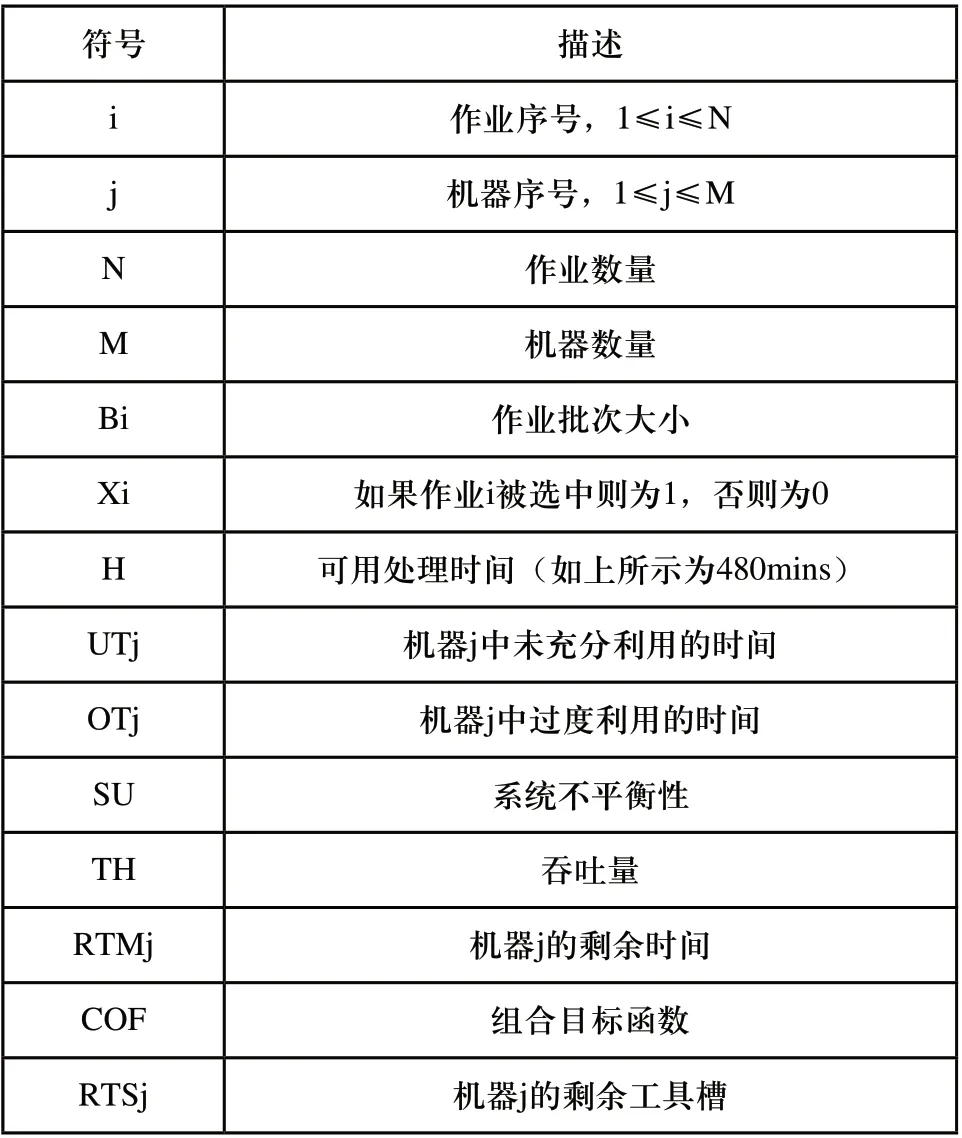
表1 符号含义图

表1(续)
本文讨论的FMS问题列于表2中。机器装载问题可以定义为:给定要生产的一组作业、给定在一组机器上处理作业所需的一组工具,用以上的资源分配简化整个系统工作流程[1]。

表2 示例FMS问题
机器装载问题通常被表述为二元目标问题,问题包含两个主要目标函数,即系统不平衡性最小化和系统吞吐量最大化,并且细节如下[2]:
最小化系统不平衡性:即使得分配所有可行的作业后机器上剩余的空闲时间的总和,而系统中机的剩余时间总和必须是0(即实现系统中所有机器100%利用率)或是一个可以接受的数值。
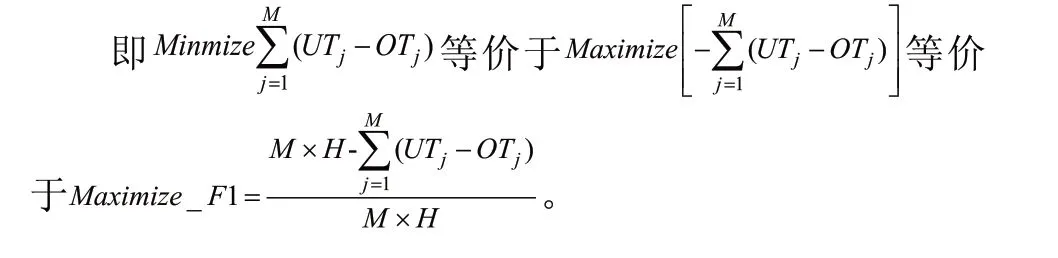
最大化吞吐量:即使得计划范围内所有选定作业的批次大小的总和最大。
即:
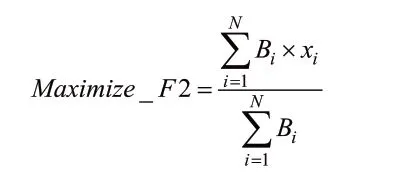
因此组合目标函数(COF)为:

文献[1~11]使用十个数据集来测试他们的方法的性能。而本文也使用相同的数据集来评估所提出的算法的性能。
2 混合进化启发式算法
在其他文献中,研究人员提出了两种启发式方法来选择某一操作是否可以在几台机器上进行。Swarnkar和Tiwari根据机器中最高可用时间选择机器[1],MukopaDyayet等人实现了在可选操作的情况下根据操作所占的重要性比率选择机器的方法[2]。本章主要描述了GASA的混合算法在解决机器装载问题中的应用,同时讨论了有关混合GASA算法实现过程中的各种设计问题。本文所提出的模型的结构如图1所示,并在本章中讨论了模型中各种模块的实现。为了通过实例说明算法流程,本文采用的数据集如表2所示。
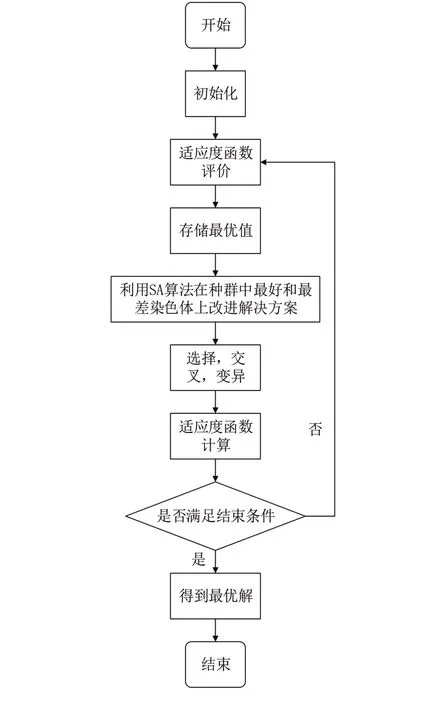
图1 混合进化启发式算法GASA流程图
2.1 初始化
首先采用最短处理时间(SPT)规则生成初始序列,SPT规则所需的每个作业的总处理时间,已在表3中给出[12]。随后以从最低处理时间到最高处理时间的升序排列作业。以表3给出的作业序列为例,生成的排列后的初始序列如图2所示。而生成初始序列后,采用循环移位法生成其他n-1个序列,其中n=N。由于程序中的种群大小固定为10,而之前的操作只能产生6个种群,因此剩余的染色体是随机产生的,而生成后每一个随机产生的染色体用现有染色体检查,避免染色体重复。
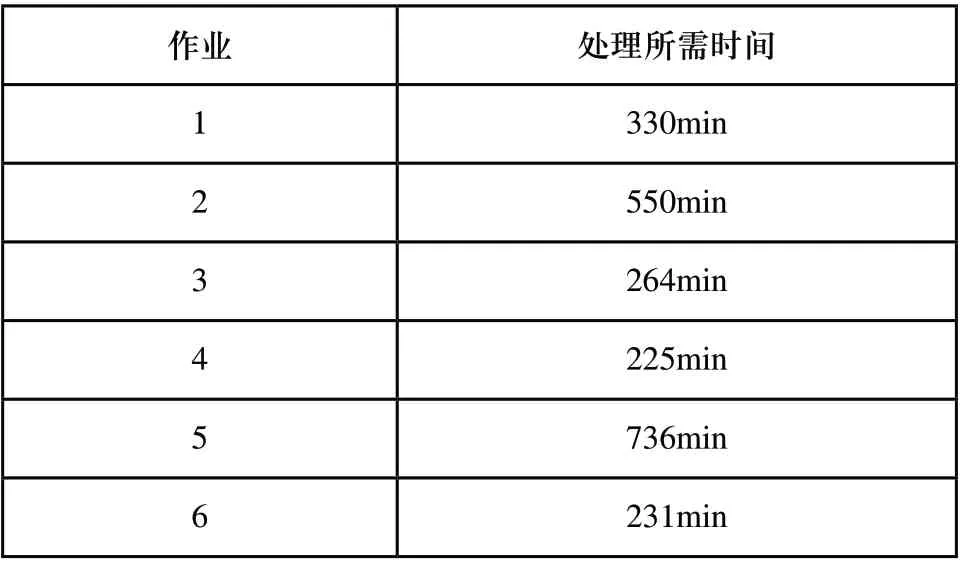
表3 作业所需的加工时间
2.2 适应度评价
通过目标函数作为约束条件确定染色体的适应值。目标函数的具体公式在上文已给出。
2.3 启发式机器选择
例如,考虑序列S=[6 1 5 2 3 4]。表4给出了每台机器上可用的加工时间和刀具槽。

表4 四台机器的加工时间和刀具槽
以第6号作业为例进行计算:
由表1可知,作业中的子工序为11,必要操作数为1,可选操作数为0。对于必要操作1,可用的机器编号为2,T2=480-21×11=249,t2=5-3=2。由于RTS1=5>0,RTS2=2>0,RTS3=5>0,RTS4=5>0;同时RTM1+RTM2+RTM3+RTM4=480+249+480+480=480=1689>=0。表示第6号作业选择完毕。而在分配第6号作业之后可用的处理时间和工具槽在如表5所示。
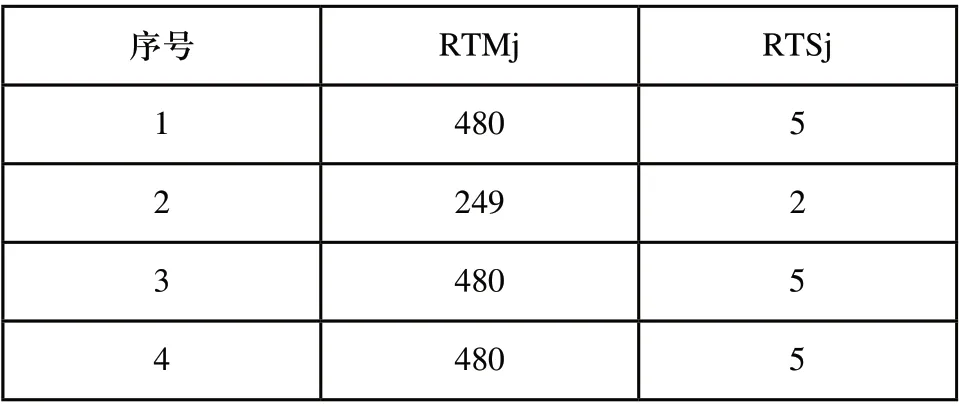
表5 选择作业6后四台机器的加工时间和刀具槽
随后我们对第1号作业进行计算:
作业中的子工序为15,必要操作数为0,可选操作数为1。对于可选操作1,可用机器是4和2。在可选操作的情况下,采用启发式方法选择可用机器,启发式方法的工作方式在图3中给出。根据计算选取比值最高的机器,由图3可知选择机器4来执行可选操作。T4=480-10×15=330,t4=5-2=3。由于RTS1=5>0,RTS2=2>0,RTS3=5>0,RTS4=3>0,并且RTM1+RTM2+RTM3+RTM4=480+249+480+330=1539>=0。表示第1号作业选择完毕。而在分配第1号作业之后可用的处理时间和工具槽在如表6所示。
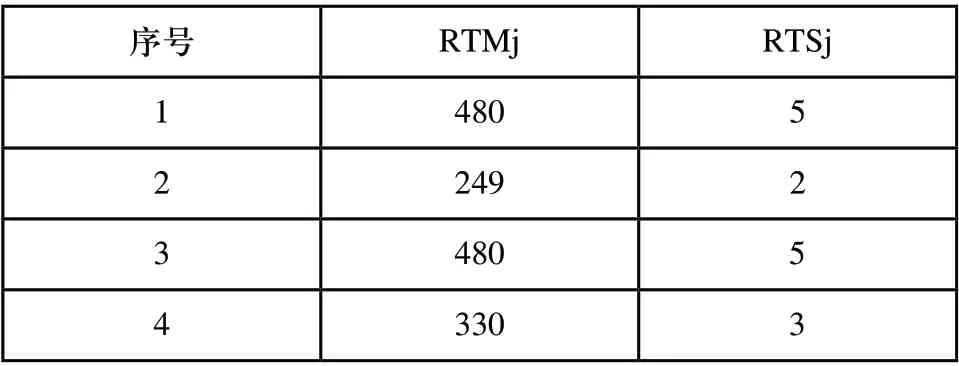
表6 选择作业6后四台机器的加工时间和刀具槽

图3 作业1选择示意图
按照同样步骤完成对所有工序的机器选择和作业分配,最终机器上可用的加工时间和刀具槽如表7所示。此时已分配的工作序列AS=[6 1 5 2 3],未分配的工作UAS=[4]。
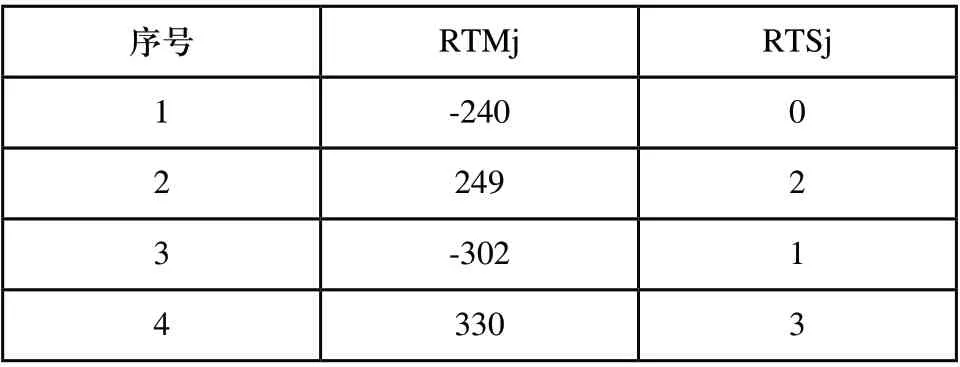
表7 分配作业完毕后加工时间和刀具槽
此时目标函数值的计算过程如下:
系统不平衡性等于所有机器分配后所有机器的过度使用或未充分利用时间的总和。从表7中,机器1和机器3被过度利用,机器2和机器4未被充分利用。因此,SU=(240 +249302+330)=37。
吞吐量等于产生的工作单位。分配的作业AS=[6 1 5 2 3]。因此,TH=11+15+16+10+12=64。
目标函数等于适应度值为(TH/所有作业的总和)+(1-(SU/工厂中所有机器的可用时间总和))=(64/73)+(1-(37/1920))=0.8767+0.9807=1.8574。
2.4 模拟退火算法
模拟退火算法的本质为接受劣解以清除局部最优通道并接近全局最优,模拟退火算法在本流程中的主要功能为:将染色体群体中提取的最优和最差序列通过模拟退火算法选择出来[13]。模拟退火算法中,初始温度T在过程开始时设定为10。温度T是一个参数,其作用类似于迭代每次减少0.9。温度T每获得一个新值,进行一次迭代。对于每次迭代,染色体S将会生成一个邻域(S')。将解S'与当前最优解S进行比较,如果S'的目标函数值优于S,则自动替换S'为当前最优解。否则,按照接受概率来接受S'。因此,当温度T较高时,较低的解决方案被接受的可能性较高。通常冻结温度可以根据程序所需的迭代次数来确定,本实验设直到温度低于0.7时迭代中止。一旦温度降到冻结温度以下,将染色体S作为当前最佳染色体返回到种群。这个过程同时作用于效果最优的和效果最差的染色体上,采用循环移位摄动法生成邻域,且其接受概率为e(delta/T)。
2.5 选择、交叉与变异
选择操作将决定进化过程的流程,为遗传算法提供了驱动力。在过去的二十年中,研究者们已经提出了许多选择方法。经过验证和比较之后本文提出的GASA采用简单的轮盘赌选择方法。本研究根据文献[12]采用了四个不同的交叉算子:循环交叉,部分映射交叉,线性顺序交叉和边缘重组交叉,交叉概率为0.7。GASA从这四个交叉算子中随机选择。此外文献[14]也提供了三个变异算子:相互交换突变、插入突变和反转突变,突变概率为0.3。GASA从这三个变异算子中随机选择。
3 结果与讨论
经过实验和比较,GASA的最优控制参数如表8所示。同时本文采用文献[1~11]中的数据集对所提出的GASA性能进行评价,并与文献中采用的启发式算法进行比较,结果如表9所示。
从表9可以看出,本文提出的GASA对于对于被测试的10个数据集中的7个能够达到最佳解,表9最后一行中的平均COF(1.7401)表示本文提出的其优于考虑用于评估的其他启发式的性能。
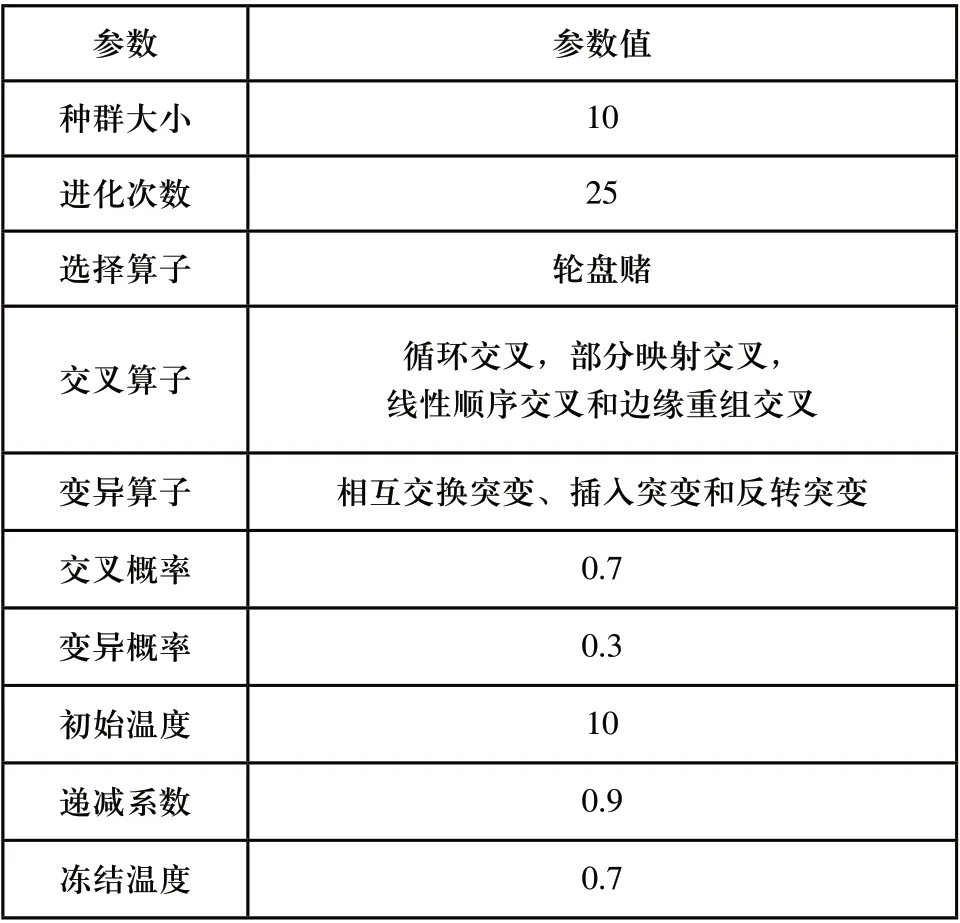
表8 GASA中各项参数

表9 GASA算法与文献中算法的比较
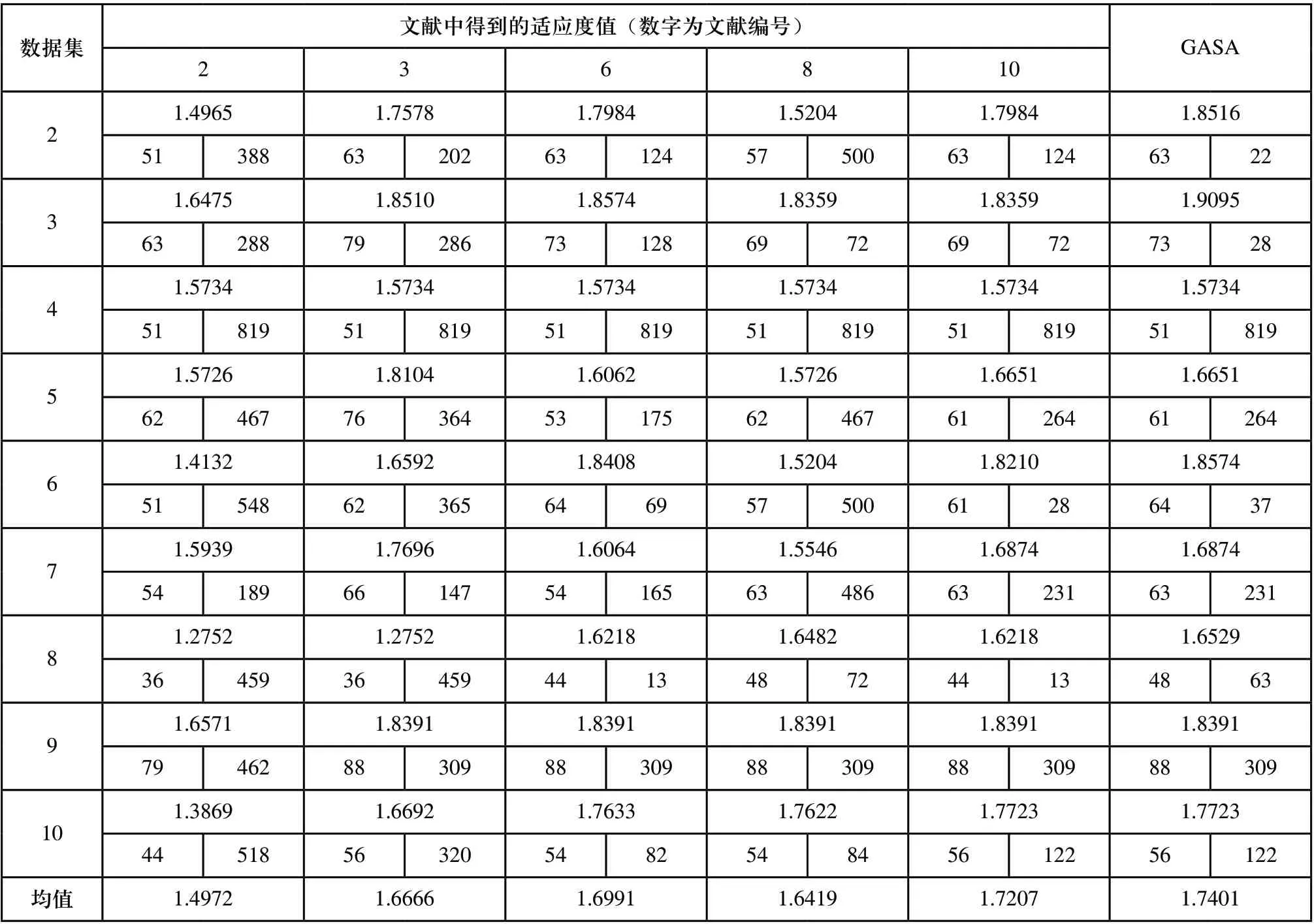
表9(续)

