基于可拓学的大型复杂航空飞行器效费权衡研究

王剑，郭鹏，党宁

(西北工业大学 管理学院，西安 710129)

0 引 言

新兴技术在航空工业的广泛应用使得大型复杂航空飞行器的功能和性能水平达到了前所未有的高度，单一追求功能或性能目标已不符合当今航空装备发展变革的需求[1]。新一代大型复杂航空飞行器的发展目标是追求费用、功能、进度、性能等多维度权衡，实现大型复杂航空飞行器的经济可承受性。所谓经济可承受性是指研制、生产、使用与维修的全过程必须在效能与经济性之间保持平衡，可定量地表达为能力与全寿命周期费用之比[2-3]。经济可承受性分析通过确定可行的性能、费用、进度及风险的权衡，对关键性决策提供了有力支持。同时，经济可承受性分析关键是与任务需求方即军方精诚合作，完成费用、性能和进度的有效权衡，其基础是需求分析，其重点是全寿命周期费用管理和效费权衡分析，同时还包含了风险分析的部分内容[4]。实际上，经济可承受性的内涵随着航空武器装备体系的不断升级和发展也在不断扩展。狭义的经济可承受性指的是将单个航空武器装备产品的费用作为独立变量进行考虑[5-6]。广义的经济可承受性指的是用户在一定的资源约束条件下，对航空武器装备体系的合理性、各机种之间配比的科学性的分析与规划[7-8]。

发达国家尤其是美国，早在20世纪60年代就开始了关于复杂飞行器效费权衡的实践与研究。在第三代轻型战斗机F-16的研制计划中，美国国防部利用现代飞机效费权衡的方法取得了很好的效果，使飞机的全寿命周期费用节省约42亿美元[9]；理论方面，效费权衡实现了三大突破：从强调性能到重视效能，从仅重视研制生产费用到强调全寿命周期费用，着眼于效能与全寿命周期费用的统一。韩庆兰等[10]提出，随着军事需求的不断提高，军用飞机的特性也在不断发展，采用CAIV作为独立变量的优化方法，设计了生命周期效费权衡的方案。在满足作战总需求下允许通过权衡适当调整费用与性能的指标，从而将军用飞机的效能与费用高度统一起来，但在具体的表征和度量中，效能与费用仍然是相对独立的特性；卢文斌等[11]认为，进行飞行器费用-效能分析的一个非常重要的问题就是装备最优化准则的建立，其采用DEA数据包络方法筛选了武器装备效费权衡方案，并应用效率评价指数比较了方案的有效性。

效费权衡分析作为经济可承受性分析的核心内容，同时也是大型复杂飞行器系统成本费用和效能管理的基础。本文利用可拓学评价模型，评估大型复杂航空飞行器效费，主要开展以下工作：(1)比较效费权衡分析的一般方法及适用条件，提出将可拓学理论应用于复杂飞行器效费权衡分析的可行性和总体框架；(2)构建基于多维物元的效费评价模型和基于物元变换的飞机效费方案延拓模型，并提出飞机效费方案可拓分析的思路；(3)引入飞行器算例，构建效费评价指标体系，检验物元方法的适用性。

1 效费比权衡分析及主要方法

1.1 效费比权衡分析的概念

若单独从费用的角度看问题，飞行器的全寿命周期费用越低越好，因而会得出飞行器越简单越好的结论；而如果单独从效能的角度看问题，则飞行器的效能越高越好，因而会得出装备越先进越复杂越好的结论。因此，必须从装备寿命周期费用和效能两个方面来综合考虑飞行器的效费比概念，可将其定义为

M=E/C

(1)

式中：E为飞行器效能；C为飞行器费用，一般指飞行器装备寿命周期费用。

由此可知，效费比是飞行器效能与费用的比值。在使用效费比开展飞行器发展、项目管理等决策时，方案的效费比高，则说明其投入越少，产出越高，该方案就越好。

效费分析是指对飞行器的费用和效能及其影响因素进行分析，寻找效费比最高的方案，提高国防资源的利用率。通过效费分析，不仅可以评价不同型号飞行器或同一型号飞行器的不同方案的优劣，还可以确认影响飞行器效费比的主导因素，并通过科学合理的调整和优化，寻求实现最高效费比的方案和途径。

1.2 效费权衡分析的主要方法

常用的效费权衡分析方法有效费指数法、比例模型法等，两类方法的基本原理和适用条件如下。

(1)效费指数法

由于飞行器费用和效能的量纲不同，效费比的数值会因采用不同的量纲而发生变化，给直接观测与比较带来一定困难。为此，需要进行无量纲化处理，定义效费指数为

(2)

式中：M(E)为效能指数；M(C)为费用指数。

效能指数和费用指数又可分别表述为

(3)

(4)

式中：C基准、E基准为设定的基准飞行器费用和效能；C和E为待评价飞行器的费用和效能。

(2)比例模型法

在飞行器研制和生产中，通常会面临多种备选方案。对于某一给定的备选方案，若满足式(5)，则表明产出大于投入，认为该备选方案是一种可行方案。

(5)

式中：M(Mi)为第i个飞行器备选方案的效费指数；M(Ei)为第i个飞行器备选方案的效能指数；M(Ci)为第i个飞行器备选方案的费用指数。

其物理意义如图1所示，射线OA上各点均有M(M)=1.0，即M(C)=M(E);由于在射线OA上方区域内的各点M(M)>1.0，则必有M(C)M(E)，即投入大于产出，代表不可行方案的集合，为不可行区域。

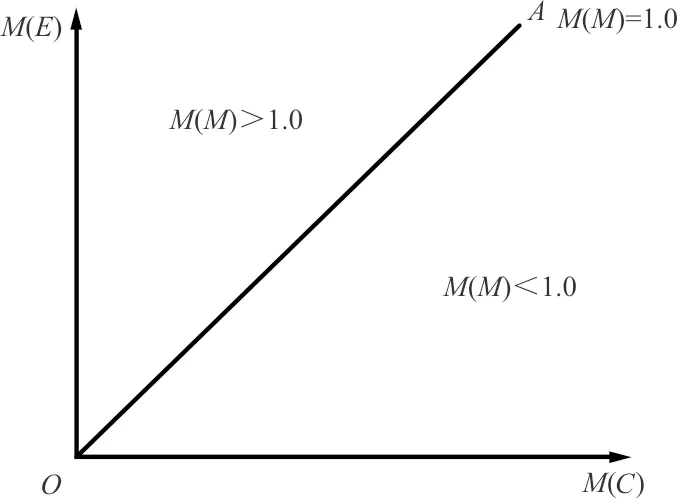
图1 比例模型的物理意义Fig.1 Physical significance of proportional model

在实际的飞行器建设决策过程中，通常受到一些条件的约束，而最大费用和最小效能是最常见的两个约束条件。其中，最大费用约束为M(Ci)≤M(Cmax)；最小效能约束为M(Ei)≥M(Emin)。最大费用约束和最小效能约束共同决定了备选方案的可行域，如图2所示。

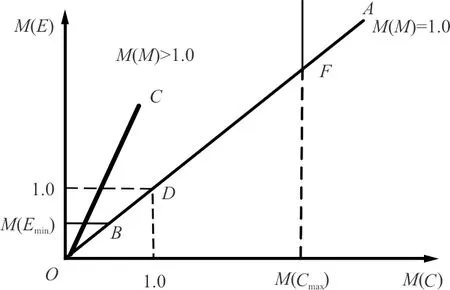
图2 基于比例模型的效费权衡分析的可行域Fig.2 Feasible region of cost-effectiveness balance analysis based on proportional model

图2中，横、纵坐标轴上各有一个值为1.0的点，分别表示规格化的航空飞行器效能M(E)和全寿命周期费用M(C)值均等于1.0，将其作为规格化的基准效能和规格化的基准全寿命周期费用。分别过横、纵坐标轴上1.0的点作垂线交于D点，连接OD使之交于过M(Emin)的水平线于B点，延长OBD使之交M(Cmax)垂线于F点，由于OBDF及其延长线上各点其效费指数M(M)均为1.0，故称之为基准线。自O点向基准线上方作任一射线OC，其上各点有：

M(M)OC=const

(6)

即在任一射线上其效费指数均相同。这样按照比例模型的判据，便可得出同一射线上各点所代表的设计方案的优劣相同的结论。但应注意，在同一射线上的各点，离坐标原点越远的点，其效能值越大，方案的技术含量越高。当然，效能的提高也会使费用有所增加，只是效能和费用的增长速率相同，才使得效费指数不变。

2 可拓学方法在飞机效费权衡分析中的应用思路

2.1 总体架构

飞行器的全寿命周期中，无论是在论证研制，还是在生产制造、使用保障以及退役处置等阶段都涉及大量的决策问题。研究决策问题，一个很重要的方面就是研究如何解决系统的矛盾问题，化不利因素为有利因素，最大限度地实现系统的最优组合和利用。效费权衡分析是一项综合性很强的工作，在这项多决策范畴工作中，需要权衡各影响因素间的复杂关系。

可拓学是由我国学者蔡文教授创立，以不相容问题为研究重心，基于将不同的矛盾要素转化为相容问题的基本思想，从形式化角度去研究矛盾的变化，从定性与定量两个方面去研究解决矛盾问题的规律和方法[12-13]。可拓学的理论支柱是物元理论和可拓集合理论，其逻辑细胞是物元。物元是描述事物的基本元，由事物N，特征c以及量值v构成的三元组R=(N,c,v)来表述。事物的变化称为开拓，事物变化的可能性称为可拓性，事物的可拓性以物元的可拓性来表征。物元模型构造了整个效费分析的逻辑细胞，方便了问题的描述与分析。基于物元可拓性的飞机效费方案延拓正是从一个已有方案信息搜索、开拓更佳方案的过程，这一过程属于可拓学菱形思维方法的发散阶段。经过这一过程，方案空间得以放大，展拓了选择的余地，潜含了产生更优方案的可能。在随后的物元聚类中，发散得到的方案集合得以聚合，形成方案集合的粗略结构。在聚类结果的基础上，再选取各类方案中具有代表性的方案参与方案的优度评价，实现菱形思维的收敛过程。上述过程经过多次反馈和迭代修正，最终形成飞机效费方案的满意解，如图3所示。

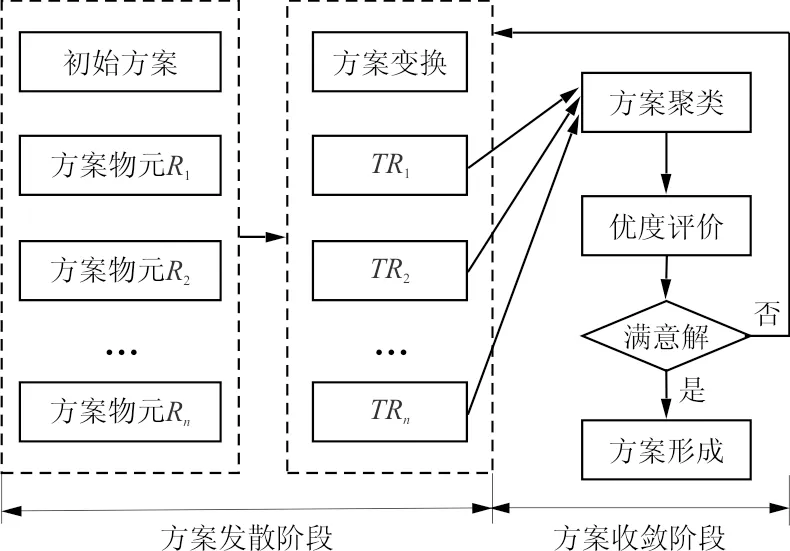
图3 飞机效费权衡分析可拓工程方法总体框架Fig.3 Overall framework of extension engineering method for aircraft cost-effectiveness balance analysis

2.2 高阶复合物元可拓模型及应用过程

2.2.1 基于多维物元的效费方案评价

飞行器效费权衡分析需要对飞行器的各种备选方案进行评价，并逐步进行分析与比较，进而使选择的方案获得满意解。其实质是通过定义和使用可行的权衡空间，充分利用现实的和潜在的因素，降低费用或者提高效能。权衡的目标是在相同的费用下获得更高的效能，或者在相同效能下获得较低的费用，两者必居其一。建立飞行器的效能和费用高阶多维物元模型：

(7)

式中：Npro为飞行器效费方案；E为效能；E(Npro)为效能度量；C为飞行器全寿命周期的费用；C(Npro)费用度量值。

模型可分解为效能物元模型和费用物元模型。由于效能是采用可用度A、可信度D和固有能力C描述的，效能物元模型可表述为

(8)

同理，若将费用按飞行器系统功能单元分解为硬件研制费CH、配套设备研制费CE和软件研制费CS，费用的物元模型则可表示为

(9)

除此之外，还可按需求对每一项目做进一步的分解，建立更低阶的物元模型。

将效能物元和费用物元代入方案物元模型，以实现方案物元的降阶，降阶后的方案物元成为一个六维的低阶物元模型。

(10)

2.2.2 基于物元变换的飞机效费方案延拓

在考虑优化效费方案时，可以采用价值工程理论。从物元分析的观点来看，价值工程的本质是从物元的可拓性出发，通过物元变换提高事物的价值。飞行器效费方案的高阶多维物元模型可表示为

(11)

价值工程的基本思想是利用方案物元的发散性，寻求方案Nx来代替Npro，使

cE(Nx)⟹cE(Npro)，其中有：

(12)

(13)

同时，E(Nx)∈A，A为指定的范围。上述过程可表述为求解Nx满足cE(Nx)≥cE(Npro)且E(Nx)∈A，要求的解集：{Nx}={Nx|E(Nx)∈A，cE(Nx)>cE(Npro)}。

这种没有降阶的方案分析方法，实际上是以效费比的概念来开拓和比较各个方案物元。

降阶后的方案物元由6个特征元组成，即Npro=(M1,M2,…,M6)。由飞行器的效能计算模型和研制费用估算关系式，得到效能和研制费用的量值:E=fE(Npro)=fE(M1,M2,…,M6),C=fC(Npro)=fC(M1,M2,…,M6)。

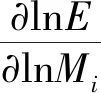
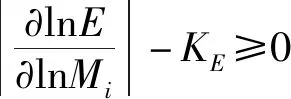
(14)

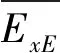
(15)

式中：KC为费用影响阈值。

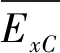
表1 特征元影响程度分析Table 1 Analysis of influencing degree of feature element

2.2.3 飞机效费方案可拓聚类分析

(1)方案物元间相似性的测度

为了对飞行器效费方案进行优度评价，可应用聚类分析的方法，对效费方案进行分类。分类时要综合权衡效费方案物元的六个特征元。为了实现对方案物元相似性的测度，可采用Minkowski距离公式(式(16))来衡量物元在特征空间的亲疏程度。

(16)

p= 1,p=2,p=∞分别对应绝对值距离、欧氏距离和切比雪夫距离。

(2)方案物元的可拓关系

建立效费方案物元的可拓关系是解决效费方案聚类问题的关键。设W1、W2是两个效费方案物元集，在W1×W2上规定一个到实域R的映射K，如式(17)所示。

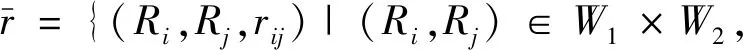
(17)

式(17)为W1与W2之间的一个二元可拓关系。当W1=W2=W时，是以W为基的二元可拓关系。可拓关系的实质是一个可拓集合，它是描述效费方案物元集内效费方案物元关系的工具。

(3)效费方案可拓聚类分析

对集合中的元素进行分类的一个重要原则是按相似性进行划分。以上所建立的可拓关系是以方案物元的Minkowski距离为基础的。距离dp(Ri,Rj)越小，表明效费方案间的相似性越大。为了对效费方案进行分类，定义相似系数rij。效费方案物元的平均距离为

(18)

平均距离为相似性的中界点，对应的相似系数为0，建立如下从效费方案物元距离到相似系数的映射关系：

(19)

r={(Ri,Rj)|(Ri,Rj)∈W×W,K(Ri,Rj)≥0}

(20)

(21)

={(Ri,Rj)|(Ri,Rj)∈W×W,K(Ri,Rj)=0}

(22)

对任意的Ri,Rj∈W，若(Ri,Rj)∈r，则Ri、Rj属于同一类，否则不属于同一类。按此原则实现对效费方案物元集合的划分，称为对效费方案物元集合按阈值x的划分。显然，x值不同，分类的方式也不同。按上述定义对效费方案的分类即为基于可拓关系的可拓聚类分析法。选取不同的阀值，能作出效费方案物元聚类谱系图，实现对效费方案分类的直观显示。

3 算 例

以某飞行器为例，验证可拓学及物元方法在效费权衡分析中的可行性，并利用可拓学的优度评价法对飞行器效费方案进行权衡分析，选择最优的效费方案。

3.1 飞行器效费权衡分析指标体系构建

3.1.1 效能指标构成

为综合分析飞行器效能影响因素，构建飞行器效能评估指标体系。其中，一级指标由固有能力、可用性、可信性指标构成：①固有能力指标。固有能力是在已知执行任务期间系统状态的情况下，系统完成任务能力的量度，即能力是系统各种性能的集中表现；②可用性指标。可用性是开始执行任务时系统状态的量度，与可靠性、维修性、维修管理、维修人员数及其能力水平、器材备件供应等密切相关，是飞行器可靠性、维修性、保障性、耐久性等的函数；③可信性指标。可信性是在已知开始执行任务时系统状态的情况下，在执行任务过程中的某一个或某几个时刻系统状态的量度，可信性与任务可靠性、生存性、环境适用性有关。

3.1.2 费用指标构成

根据调研及相关文献研究，提炼飞行器全寿命周期费用，包括：①人工成本。人工成本主要包括研制员工的工资、津补贴、培训费等工资性支出。其中，研制员工工资=年从事研制工作的员工数×研制年限×年人均工资水平；津补贴、培训费等一般按照员工工资比例计提。②材料成本。材料成本包括在研制过程中产生的原材料成本、辅助材料成本、外购材料成本、燃料动力成本等。其中原材料是指在研制过程中直接用于制造，且构成系统实体的材料；辅助材料是指在研制过程中辅助制造，但最终不构成系统实体的材料；燃料成本是指用于购买研制所需的燃料、电力、能源的成本。③管理成本。管理成本是指在研制期间应分摊的管理费用，包括办公成本、会议成本、差旅成本等。其计算公式一般为按比例折算提取。

根据上文所形成的飞行器效能及费用评价指标，依次设置各评价指标代号，构建飞行器效费评价指标体系，如表2所示。

表2 飞行器系统效能及费用评价指标体系Table 2 Index system of evaluation of aircraft system effectiveness-cost

3.2 指标量值和权重确定

在现有统计资料和实验数据的基础上，确定飞行器效费方案A，B，C和D，关于其评价指标的量值如表3所示。

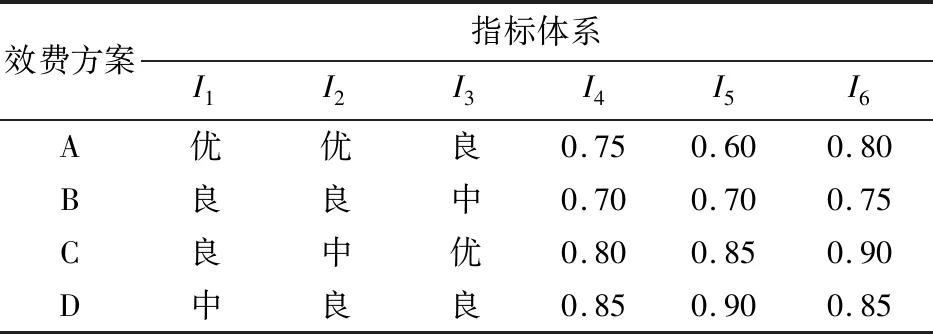
表3 飞行器效费指标体系Table 3 Index system of aircraft’s effectiveness-cost

根据有关资料和经验数据，确定测度的相对标度，依据经验数据，应用AHP群体决策法构造一级指标两两比较判断矩阵，如表4所示，其中W为指标权重向量；CI为判断矩阵的一致性指标；CR为判断矩阵的随机一致性比率。

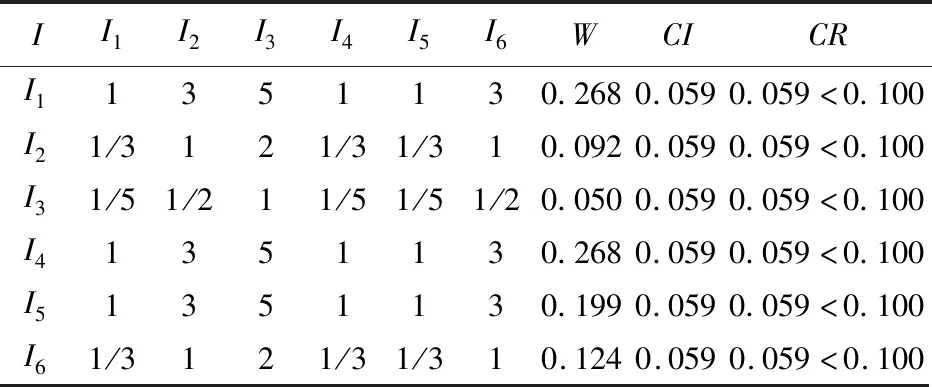
表4 I～Ii判断矩阵Table 4 Judgment matrix of I～Ii

根据计算，由表4可知确定评价指标I={I1,I2,I3,I4,I5,I6}的权系数为α={α1,α2,α3,α4,α5,α6}=(0.268,0.092,0.050,0.268,0.199,0.124)。

3.3 合格度计算

3.3.1 特征合格度

关于效费方案优劣衡量条件M，指标I某特征元量符合要求的量值范围为X0；不符合要求，但可转变为符合要求的量值X’，量值允许的取值范围为U。以X0为经典域，X’为可拓域的可拓集合，描述U上任一个值u符合要求的程度，设其关联函数值为KX0，称它为u关于衡量条件M的合格度。

根据方案各指标的量值，建立指标与目标的关联函数。指标I4，I5，I6与目标的关联函数为

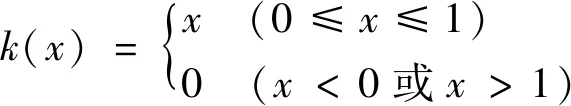
(23)

而指标I1，I2，I3与目标的关联函数为

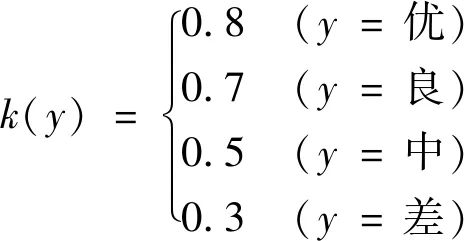
(24)

将飞行器效费方案 A，B，C 和 D 关于评价指标的取值代入相应的关联函数中，求出权衡目标关于评价指标的关联度，得

3.3.2 规范合格度

效费方案指标量值关于目标I的合格度K(I)计算如下：

(25)

得出各方案的指标量值的合格度为

3.4 飞行器效费方案的优度评价

方案物元Nj(j=1,2,…,m)关于衡量条件M1，M2，…,Mn规范合格度为

(26)

故效费方案物元Nj的优度为

(27)

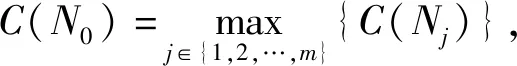
(28)

同理，C(B)=0.803，C(C)=0.896，C(D)=0.882。由测度结果可知，C(C)=max{C(A)，C(B)，C(C)，C(D)} ，故飞行器效费方案C最优。评价大小排序为C(C)>C(A)>C(D)>C(B)。

通过上述四个效费方案的分析和选择，飞行器固有能力、人工成本和材料成本对方案的选择影响较大，因此，若要优化飞行器的效费方案，主要要提高飞行器固有能力，同时要适当降低人工成本和材料成本。

4 结 论

论文提出运用可拓学理论与方法展开大型复杂航空飞行器效费权衡分析的适用性，并构建了效费权衡模型。在多重约束下，基于可拓学的优度评价方法可以遴选出复杂飞行器效费权衡的最优方案。该方法可应用于作战方案生成与评价过程中，为任务需求方促进寿命周期效费管理优化提供理论参考。