熔喷三维气流场的数值计算与分析

姬长春， 张开源， 王玉栋， 王新厚

(1. 太原理工大学 轻纺工程学院， 山西 晋中 030600； 2. 山西能源学院， 山西 晋中 030600；3. 东华大学 纺织学院， 上海 201620)

熔喷非织造技术具有工艺流程短、生产效率高等特点，近年来发展较快。熔喷纤维的平均直径可达到微米或亚微米级[1]，属于超细纤维。相比普通纤维，熔喷纤维具有直径小、比表面积大等优点，其制品结构蓬松、孔隙多而孔隙尺寸小，可用作环境净化和生物洁净的高级过滤材料[2-3]。

气流模头是熔喷设备中的核心部件，其提供的高速射流不仅决定熔喷纤维的直径，而且影响熔喷纤维的强度、结晶度等性能，因此，对熔喷气流模头下方喷射流场进行研究是探究熔喷纤维拉伸机制的基础，国内外很多科研人员致力于熔喷模头喷射流场的研究，以期细化熔喷纤维的直径。Shambaugh等[4-5]首次对双槽形熔喷模头下的低速射流场进行实验测量和数值模拟，得到了熔喷低速等温流场的分布状况。在此基础上，王晓梅[6]、陈廷[7]以及王新厚等[8-9]借助计算流体力学技术对双槽形模头的高速非等温二维流场进行数值计算发现：喷气孔宽度、喷气孔倾斜角度和喷气孔外端宽度等结构参数对纺丝中心线上速度和温度的影响较大。辛三法等[10]使用二维数值方法研究了双槽熔喷工艺中外沿长度对空气流场特征的影响。其研究表明随着外沿长度的增加，空气速度峰值和压力峰值减小。研究人员普遍对熔喷双槽形流场采用二维简化计算，具有一定的合理性[4-5]。

二维数值模拟忽略了喷气孔的2个端面对熔喷流场的影响，其计算结果不能准确地反映熔喷喷射流场的全部流动特性，因此，对熔喷流场进行三维数值模拟研究是完全有必要的。本文采用数值模拟方法对双槽形熔喷模头的三维高速高温流场进行表征与分析，以期深层次探讨熔喷纤维牵伸成形机制。

1 双槽形熔喷三维流场模型的建立

1.1 双槽形熔喷气流模头

图1示出双槽形熔喷模头的结构示意图。高温压缩空气从喷气孔进入，在模头下方形成非等温流场。本文所采用的双槽形熔喷模头的喷气孔宽度b为0.65 mm，喷气孔倾斜角度β为60°，喷气孔外端宽度h为3.32 mm，喷气孔长度l为20 mm。

图1 双槽形熔喷模头的结构示意图Fig.1 Schematic diagram of slot melt-blown die-head. (a) Cross-sectional view of slot die; (b) Top view of slot die

1.2 双槽形熔喷流场的几何模型

图2示出双槽形熔喷模头的计算域。可知，双槽形模头流场的计算域包括喷气孔空间部分和其下方的流场部分。由于双槽形熔喷模头的计算域是关于xy平面和xz平面对称的，计算域只选取整个双槽形熔喷模头流场空间的四分之一，可减少计算时间和提高计算效率。计算域的尺寸参考了前人的研究[5,11]：喷气孔空间部分的高度为5 mm；沿z轴方向的长度为100 mm，沿x轴方向的长度为30 mm，沿y轴方向的长度为13 mm。

图2 双槽形熔喷模头的计算域Fig.2 Computational domain of slot melt-blown die

1.3 模型假设与系统描述

在熔喷三维流场中，气流以可压缩、黏性、非等温湍流形式存在。通过实验测量数据与数值模拟结果对比发现，标准的k-ε湍流模型[12]可较为准确地捕捉熔喷流场中湍流流动[5,11]，因此，本文选用标准的k-ε湍流模型对流场进行计算。

在标准的k-ε方程模型中，k和ε的时均形式的输运方程为

(1)

(2)

式中：ρ为流场中的气体密度，kg/m3；k为气体传热系数，W/(m2·K)；μ为空气的动力黏度，N·s/m2；ui为气流速度矢量u在x方向的分量；i和j的取值范围为[1，2，3]；μt为湍动黏度，N·s/m2；C1ε、C2ε和C3ε均为经验常数；σk为湍动能k对应的Prandtl数；σε为湍动耗散率ε对应的Prandtl数；Gk为由于平均速度梯度引起的湍动能k的产生项；Gb为由于浮力引起的湍动能k的产生项；YM为可压湍流中脉动扩张的贡献；Sk和Sε为源项。本文中，C1ε=1.24，C2ε=2.05，其他的系数保持为默认值，可保证数值计算结果与实验测量数据一致，其余参数的单位设置和取值参考文献[11]。

2 数值计算

2.1 网格划分

使用Gambit对计算域分区进行网格划分，选用六面体网格类型；采用“Map”划分方式，并对2股射流交汇及附近的区域进行自适应区域加密。网格总数为1 421 110。

2.2 边界条件和参数设定

图2中，ABCD平面设为“压力入口”。入口处高压气流的绝对压强设为126 656.25 Pa，气体温度为 400 K。入口处边界条件中的水力直径为喷气孔的宽度，湍流强度设为10%。EE1F1F平面、FF1G1G平面和O1E1F1G1平面设定为“压力出口”。计算域出口处即为大气环境，出口处气体的压强为 101 325 Pa，气体温度为300 K，水力直径为10 mm，回流气体的湍流强度为10%。ABB1A1平面、OEE1O1平面和OGG1O1平面被设为“对称面”。计算域的其他平面设为无滑移壁面边界。壁面温度设为410 K。采用FLUENT 6.3.26进行数值模拟，计算终止条件设定为残差达到10-3。

3 结果与分析

3.1 不同xy平面上的速度、温度和压力分布

图3～6示出不同xy平面上的速度、温度和静压分布。可以看出，在xz平面内中心处的速度值、温度值和压强值较两侧区域高。熔喷纤维位于xz平面流场中心区域内时，有利于其细化。

图3 xy面上的速度、温度和压强分布(z=1 mm)Fig.3 Velocity(a), temperature(b) and pressure(c) distribution on xy plane (z=1 mm)

图4 xy面上的速度、温度和压强分布(z=5 mm)Fig.4 Velocity(a), temperature(b) and pressure(c) distribution on xy plane (z=5 mm)

图5 xy面上的速度、温度和压强分布(z=30 mm)Fig.5 Velocity(a), temperature(b) and pressure(c) distribution on xy plane (z=30 mm)

当z为1 mm时，从图中可以看出，平面上的温度和压强呈单峰状，而平面上速度有2个峰值，此时 2股射流还未融合，保持各自流动的状态；随着x值的增大，平面上的速度、温度和压强变化不显著。

随着z值的增大(5 mm≤z≤30 mm)，xy平面上的速度、温度和压强都只有1个峰值且逐渐平缓。表明2股射流已融合成1股射流，随着喷射距离增加，融合后的射流向四周扩散，中心处的射流逐渐带动远处的气体向下运动，平面上的速度、温度和压强随z值增大逐渐降低。

在流场的中心区域，不同xy平面上的速度、温度、压强随着x值的增加基本没有变化。而在远离流场中心的区域，流场中的速度、温度和压强随着x值的增大而有所降低。

当z值进一步增大时(z=50 mm)，xy平面上的速度、温度和压强峰值进一步降低。xy平面上的速度和温度随x值的增大基本没有改变，而此时平面上的压强峰值随着x轴正向略有增大。

图3～6表明：喷气孔端面(图2中的DCC1D1平面)对模头下方中心区域流场中的速度、温度和压强影响较小；而对喷气孔端面下面附近的流场作用明显。由于工厂中实际用到的双槽形熔喷模头喷气孔的长度远大于本文数值计算用到的模头的长度，喷气孔端面对流场中心区可忽略不计，模头下面的大部分流场区域具有二维流场特征。

3.2 纺丝线上的速度、温度和压力分布

双槽形熔喷模头的喷丝孔按照一定的间距分布在x轴线上，其轴线与z轴平行(或重合)。这些分布在xz平面上的轴线又被称为纺丝线。在熔喷非织造成品的实际生产中，熔喷纤维的运动路径主要在纺丝线附近[11]。本文假定喷丝孔圆心以1 mm的间距分布在位于点(0，0，0)到点(10，0，0)的区间内，来考察双槽形熔喷模头中不同喷丝孔对应纺丝线上的速度、温度和压强差异。

图7示出流场中不同纺丝线上的速度分布。可以看出，纺丝线上的速度先迅速增大，在靠近模头的区域达到一个极值后速度开始逐渐减小。对比不同位置处纺丝线上的速度可以发现：流场中心处纺丝线上的速度最高；当远离流场中心后，纺丝线上的速度逐渐降低，位于气槽端面处纺丝线上的气流速度最低。靠近流场中心位置处几条纺丝线上的速度相差不大；而x值的进一步增大，纺丝线上气流速度值与中心处纺丝线上速度值的差异性增大。这说明气槽端面对纺丝线上的速度影响很大，对整个流场的速度分布也有一定的影响。

图6 xy面上的速度、温度和压强分布(z=50 mm)Fig.6 Velocity (a), temperature (b) and pressure(c) distribution on xy plane (z=50 mm)

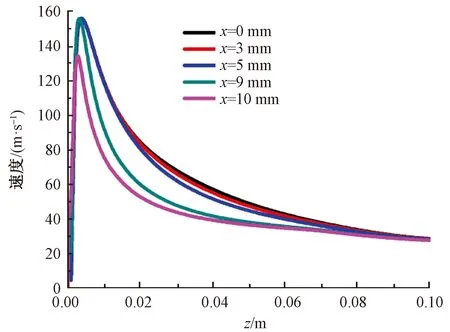
注：x=0、3、5、9和10 mm分别对应纺丝线上点(0，0，0)、(3，0，0)、(5，0，0)、(9，0，0)和点(10，0，0)，下同。图7 不同纺丝线上的速度分布Fig.7 Velocity distribution on different spinning lines

图8示出熔喷三维流场中不同纺丝线上的温度分布。可以看出，温度衰减的速度很快，气槽端面对不同位置处的纺丝线上的温度影响也很大。当远离流场中心处时，纺丝线上的温度逐渐降低；端面处纺丝线上的温度最低，且与中心位置处纺丝线上的温度差值最大。

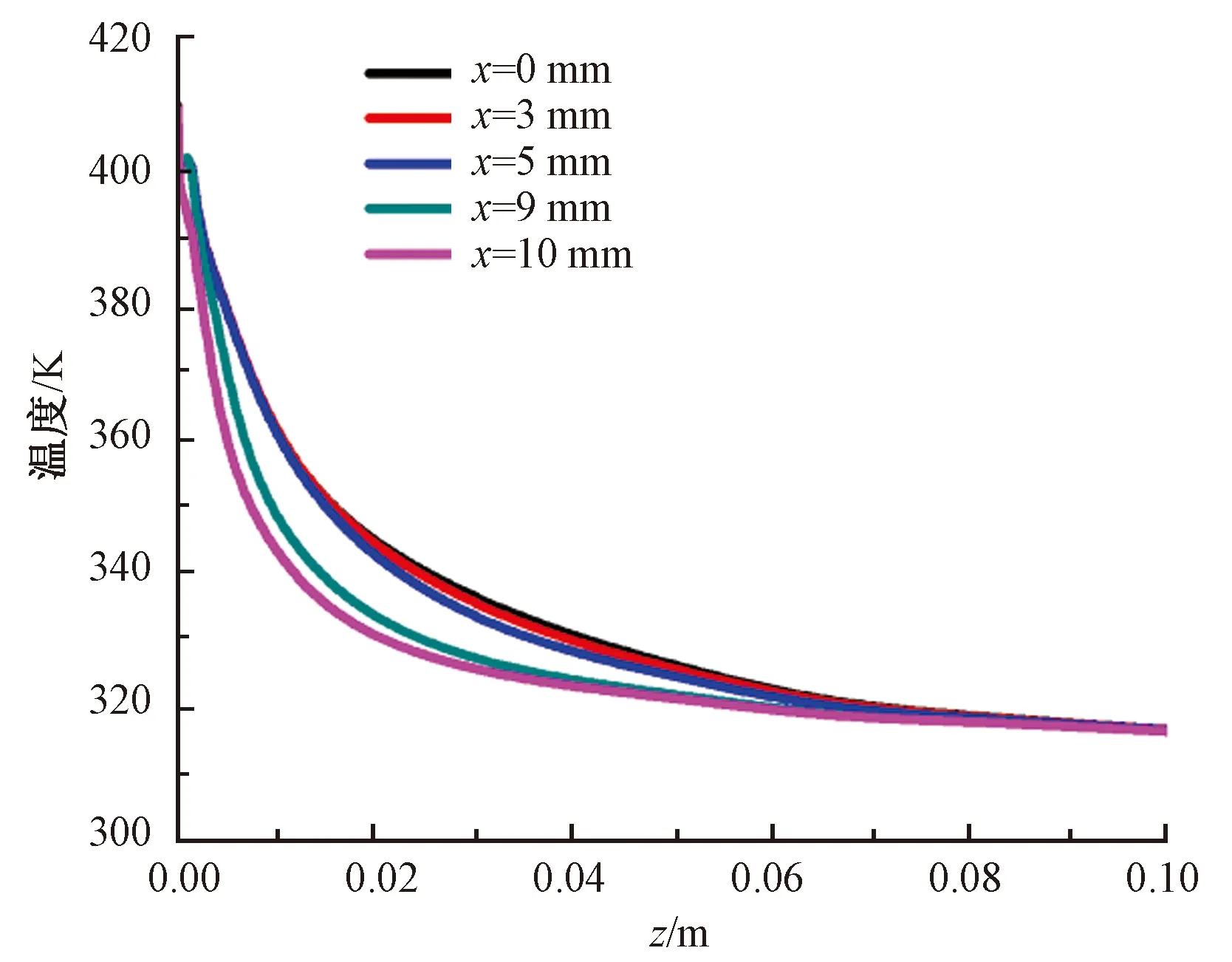
图8 不同纺丝线上的温度分布Fig.8 Temperature distribution on different spinning lines

较高的气流速度和温度有利于熔喷纤维的细化[11]，因此，流场中心区域内的气流可使喷丝孔挤出的聚合物熔体细流得到更充分的牵伸。为制备得到直径较小的纤维，喷丝孔应置于流场中心区域，远离喷气孔的2个端面。

图9示出三维气流场中静压在不同纺丝线上的分布。

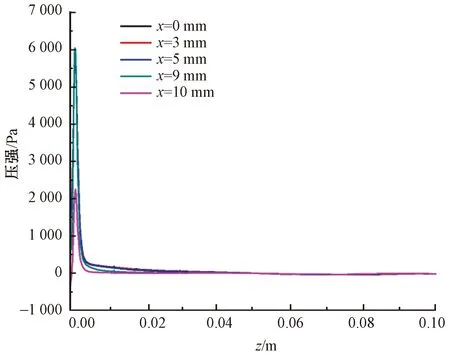
图9 不同纺丝线上的压强分布Fig.9 Pressure distribution on different spinning lines

对比图7和图9，纺丝线上静压的变化规律与气流速度的变化规律相似，均呈先急剧增大后逐渐减小。但与速度变化规律不同的是，压力极值点的位置要早于速度极值点的位置。从图9可以看出，端面处纺丝线上的静压最小，其余的纺丝线上的静压值基本一致。这说明气槽端面对纺丝线上的静压有一定的影响，但与对纺丝线上速度和温度的作用相比，效果没那么显著。

另外，熔喷流场中不同位置处纺丝线上速度、温度和压强分布的差异，易使不同位置处的聚合物熔体受到不同的气流作用力，发生不同的形变。气槽端面的影响不仅使纺制的熔喷纤维呈现不同的细度和性能等，而且影响纤维在流场中的运动路径，对最终的纤维网结构有一定影响。

4 结 论

本文应用Fluent软件对双槽形熔喷模头的三维喷射气流场进行数值计算，并对流场中的速度、温度和静压等进行分析，得出以下结论。

1)在三维熔喷气流场中，中心区域内的速度值、温度值和静压值较大。

2)用数值模拟的方法可以证明：当双槽形熔喷模头的喷气孔长度较长时，远离气槽端面区域内的非等温三维喷射气流场可简化为二维流场。

3)喷气孔的端面对不同位置处纺丝线上的温度、速度和压强分布有一定的影响。随着远离流场中心，纺丝线上的速度和温度开始下降，而静压值变化不是很显著；与流场中心附近位置的纺丝线相比，喷气孔端面处的纺丝线上的温度、速度和静压小得多，因此，双槽形的纺丝线上的速度、温度和压强分布特点，易使纺制的纤维直径和纤维性能等存在差异性。

FZXB