SAW式WTP输入及输出阻抗匹配研究

刘守兵，卢文科

(1.河南工程学院 电气信息工程学院，河南 郑州 451191；2.东华大学 信息科学与技术学院,上海 201620)

0 引言

声电式小波变换处理器(WTP)，特别是声表面波(SAW)式WTP不但能对信号进行小波变换[1]，且还具有独有的体积小，结构简单和性能可靠等优点[2]，因而其在气体检测、水位测量、雷达目标识别等领域得到广泛的应用[3-6]。为此，研究人员设计了一系列性能优良的SAW式WTP[7-8]。但是，组成这些SAW式WTP的叉指换能器(IDT)的等效电路是一个三端口网络，其插入损耗和三次渡越反射都与输入、输出阻抗有关[9]。若直接将该芯片用于电子系统中，受三次渡越反射的影响，其通带将会产生波纹，进而将该波纹引入转换后的信号中。为此，必须对SAW式WTP的输入、输出阻抗匹配进行研究。

求取SAW式WTP的输入、输出阻抗的方法很多，但大多需要借助测量器具实现[9]。为此，本文拟采用导纳矩阵来求取其输入、输出阻抗，进而由其设计相应的匹配网络。采用这种方法求取SAW式WTP的输入、输出阻抗，必须先求出该器件的导纳矩阵。但现有的导纳矩阵计算方法由于只能求取两IDT都未加权的SAW器件的导纳矩阵，而无法将其直接用于一个IDT加权的SAW式WTP的导纳矩阵[10]。为此，本文引入了通道分割法[11]，将一个IDT加权的SAW式WTP转换成一系列可等效为两IDT均未加权的SAW器件的平行通道，进而由每个通道的导纳矩阵求取整个SAW式WTP的导纳矩阵，并由其求取该器件的输入、输出阻抗，设计其匹配网络。

1 SAW式WTP的原理与设计

Morlet小波函数的时域表达式[12]为

(1)

式中：s为小波函数的尺度；f0为其中心频率；t为时间。

根据式(1)，小波函数的包络函数[13]为

(2)

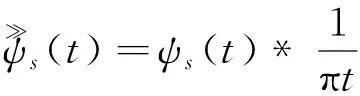
经过大量的研究[14-15]可发现，如果按照式(2)设计SAW器件的输入IDT指条重叠包络，而输出IDT采用指条相等重叠、均匀周期的电极结构，就可以设计出一个SAW式WTP。

根据式(2), SAW式WTP的声孔径长度为

(3)

式中:n为指条编号;k为声孔径长度与对应包络值比值的常数。

2 SAW式WTP的导纳矩阵

2.1 两IDT均为加权的SAW器件的导纳矩阵

SAW器件在电子系统中应用时的连接示意图如图1所示。将1个内阻抗为Zs的电压源(Vin)连接到输入IDT上，负载ZL连接到输出IDT上。从电信号传输的角度来看，该器件可等效为1个信号变换器件，可用二端口网络表示，则有

I1=y11V1+y12V2

(4)

I2=y21V1+y22V2

(5)

式中:y11、y12、y21和y22为该二端口网络的导纳参数;V1、I1、V2、I2分别为输入电压、输入电流、输出电压、输出电流。

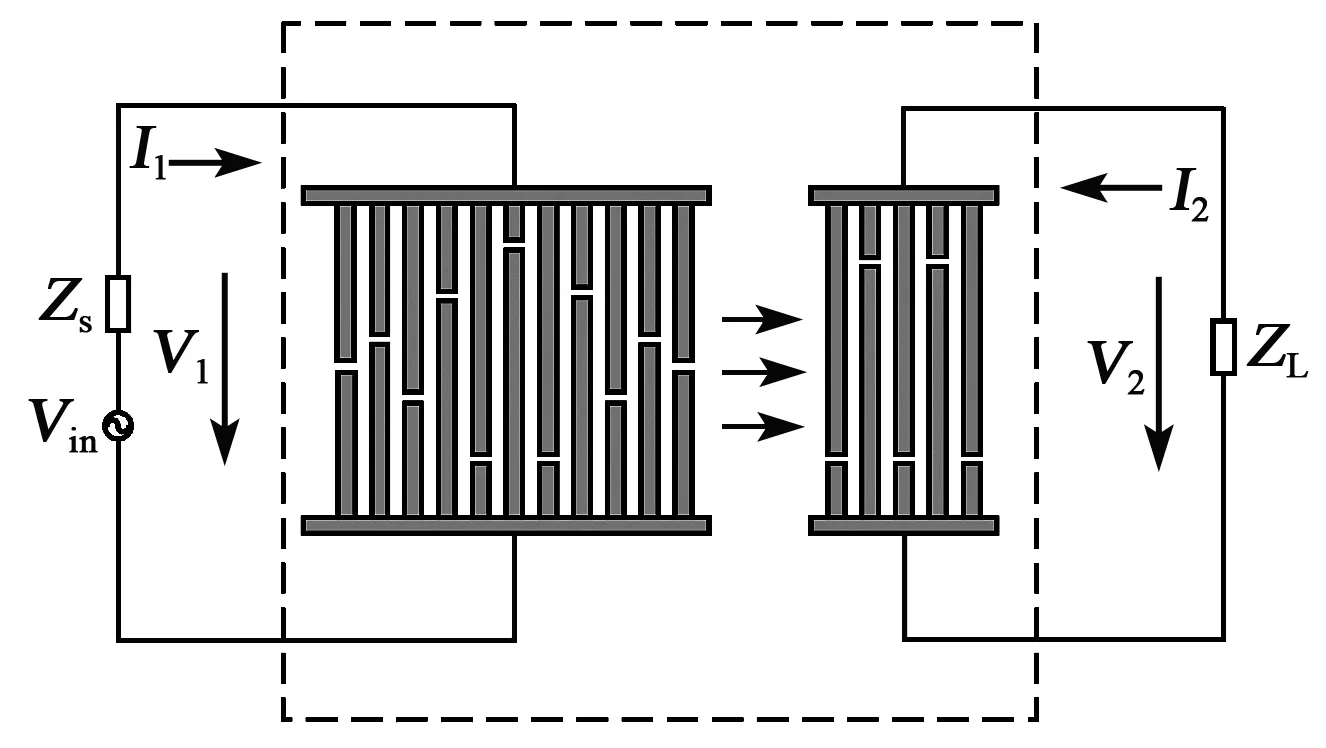
图1 SAW器件的等效二端口网络

对于两个IDT都未加权的SAW器件，这些导纳参数可通过下式计算：

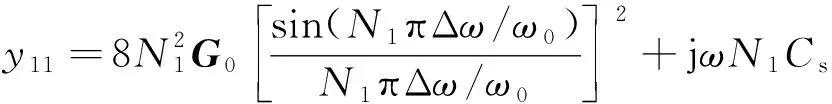
(6)

(7)

(8)

式中：N1为输入IDT的指对数；N2为输出IDT的指对数；G0=ω0CsK2/(2π)为SAW器件的特性导纳矩阵，K2为基片材料的机电耦合系数；ω0=2πvs/L为声同步角频率，vs为SAW在基片材料自由表面的传播速度，L为1个叉指周期的长度；Cs为一对叉指的静态电容；Δω=ω-ω0和Φ为由两IDT的中心距造成的相位角；j表示该部分为复数的虚部。

根据式(4)～(8)即可得到SAW器件的导纳矩阵为

(9)

2.2 SAW式WTP的导纳矩阵

由于SAW式WTP的输入IDT采用切趾加权的电极结构(见图2)，因而我们无法直接采用式(6)～(9)计算出该器件的导纳矩阵。为此，我们引入Tancrell 和Holland两位学者首创的通道分割法，并通过这种方法将SAW式WTP分割成一系列平行的通道，如图2所示。图2中，通道由水平折线标识，而通道边缘由电极边缘标识。每个通道都可以看作是一个两IDT均未加权的SAW器件，从而可以利用式(6)～(9)求出每个通道的二端导纳矩阵。

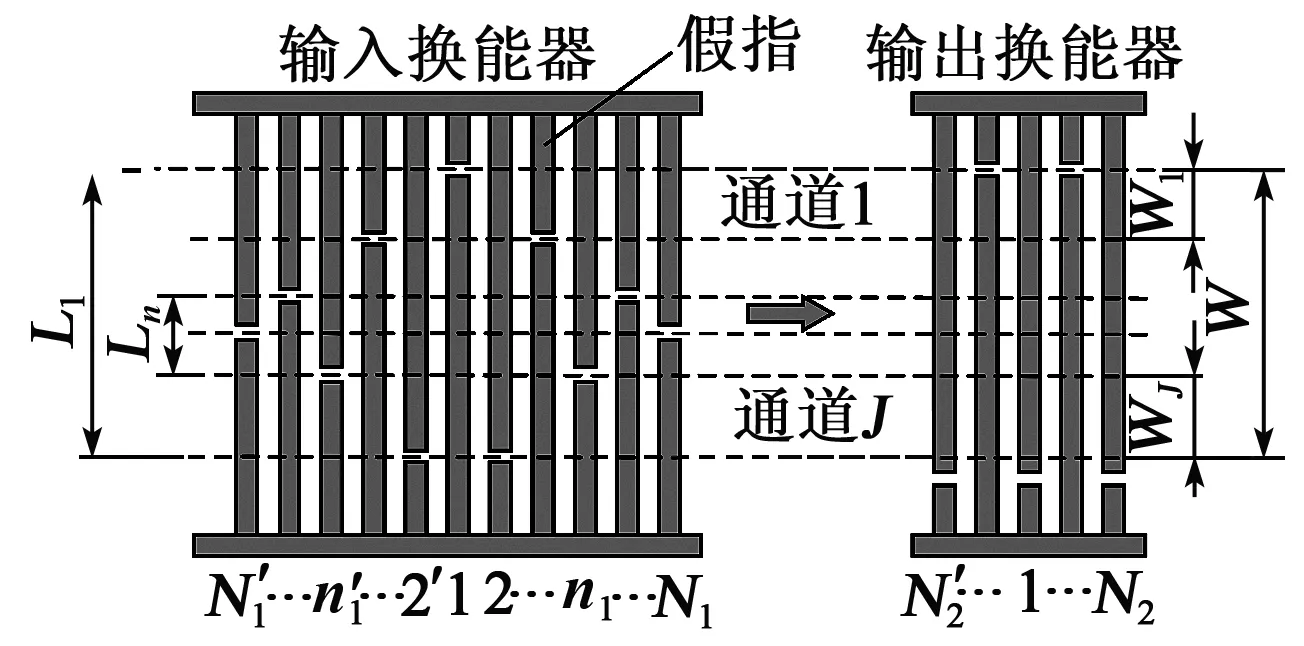
图2 SAW式WTP的结构示意图

若一个SAW式WTP的输入IDT的指条对数为Nsr，输出IDT的指条对数为Nsc，根据图2，并经适当的数学推导，可得到以下结论:

该SAW式WTP可分割的平行通道个数为

Ntd=Nsr

(10)

当通道个数Ntd为奇数时：

对于每个通道，其输入IDT的指条对数为

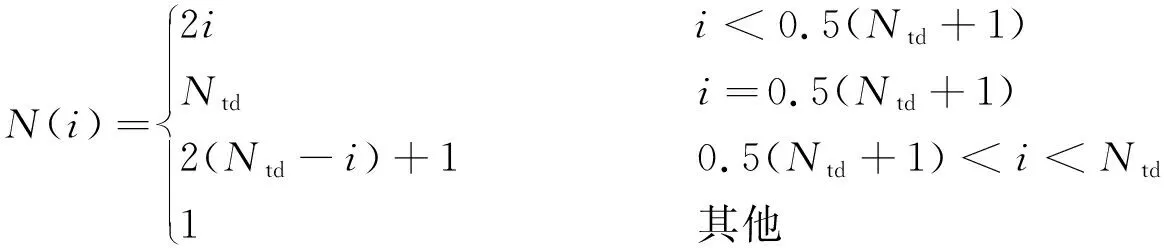
(11)

式中i为通道编号。

对于每个通道，其声孔径长度为

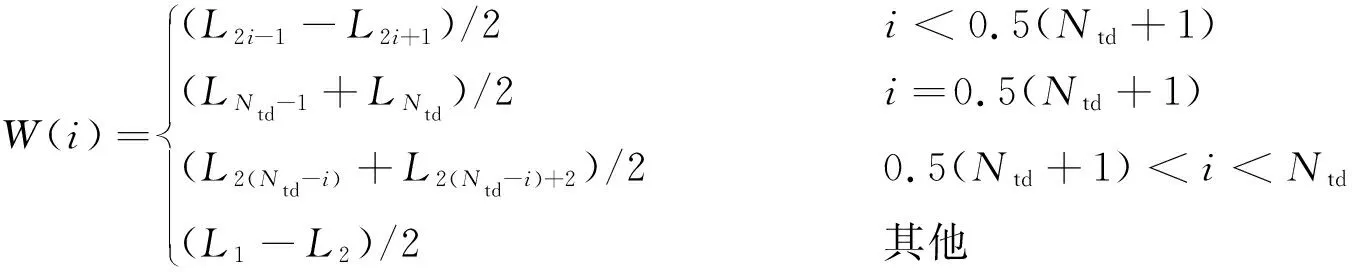
(12)

式中Li为SAW式WTP输入IDT中编号为i的指条重叠包络的长度。

当Ntd为偶数时：

对于每个通道，其输入IDT的指条对数为

4.自动驾驶功能驾驶员有不当适用，但驾驶员驾驶或操作没有过错，也没有违反道路交通安全法律法规，此种情况下交通肇事的法律责任由自动驾驶功能的制造商或供应商承担责任；

(13)

对于每个通道，其声孔径长度为

(14)

若周期段内单位长度指条的静态电容为C0，则由式(12)、(14)可计算出一对叉指的静态电容为

Cs(i)=C0W(i)

(15)

将式(11)、(13)和(15)代入式(6)、(7)和(8)中，即可得到每个通道的导纳矩阵。

依据二端口网络的简化原则，可求得整个SAW式WTP的导纳矩阵为

(16)

3 SAW式WTP的输入及输出阻抗匹配

综上所述可知，SAW式WTP可等效为一个二端口网络，且已算出该二端口网络的导纳矩阵。根据二端口网络的性质，由SAW式WTP的导纳矩阵可计算出其输入、输出阻抗为

(17)

(18)

式中conj(·)为共轭运算。

利用式(17)、(18)求取的输入、输出阻抗即可设计出SAW式WTP的匹配网络。

4 方案论证与讨论

为了验证本文提出的SAW式WTP的输入、输出阻抗匹配方案，本文专门设计了SAW式WTP的参数如表1所示。表中ε∞为介电常数。

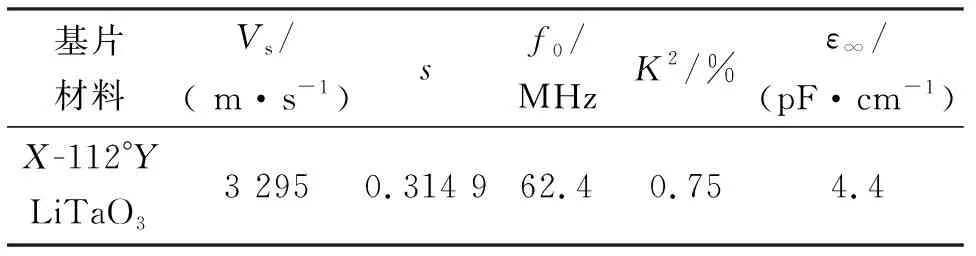
表1 SAW式WTP的设计参数

根据式(3)可设计出上述SAW式WTP，并得到该器件的Nsr和每根指条的Li，进而可由式(10)～(15)算出该SAW式WTP分割的平行通道数Ntd，每个通道内输入IDT的指条对数N(i)和一对叉指的静态电容Cs(i)。由这些参数利用式(6)～(8)计算出每个通道的导纳矩阵Yi，进而可由式(16)计算出整个SAW式WTP的导纳矩阵，即

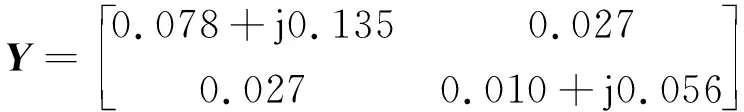
(19)

与此同时，我们还实际制作了SAW式WTP，并利用文献[4]提供的方法实际测量了该器件的导纳矩阵，则有

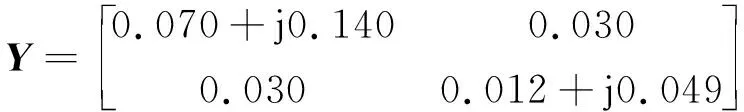
(20)

对比式(19)、(20)可知，理论计算的导纳矩阵与实测的导纳矩阵相比，其误差基本可忽略，能满足理论研究和应用的精度要求。

将式(19)代入式(17)、(18)，即可得到该SAW式WTP的输入、输出阻抗为

Zs=3.209+j5.553

(21)

ZL=3.090+j17.305

(22)

利用式(21)、(22)可设计出该器件的匹配网络。

采用文献[16]可测量出匹配前、后的SAW式WTP的插入损耗分别为31.6 dB和19.2 dB，降低了39.2%。

5 结束语

本文对SAW式WTP的输入、输出阻抗匹配进行了研究。为了求取匹配网络中需要的输入、输出阻抗，本文首先根据通道分割法将SAW式WTP分割成一系列可等效为两IDT都未加权的SAW器件的平行通道，并首次给出通道数、各通道输入IDT的指条对数和一对叉指的静态电容；然后根据这些参数计算出各个通道的导纳矩阵和整个SAW式WTP的导纳矩阵；最后根据这个导纳矩阵计算出该器件的输入、输出阻抗，并对该阻抗的SAW式WTP的插入损耗的影响进行了验证。理论研究和实验结果表明，利用这种方法设计的SAW式WTP的匹配网络，可以使该器件的插入损耗降低30%以上，因而其具有显著的理论意义和应用价值。