高强度钢材钢框架梁柱节点抗震性能研究

高志远，郭宏超，王德法，梁 刚

(西安理工大学 土木建筑工程学院，陕西西安710048)

在实际工程中，运用的全部梁柱连接都处于完全刚性和理想铰接之间，而作为带加劲肋顶底角钢是一种独特的钢结构节点连接形式，随着钢材强度的提高，节点域展现出一种新的特性。

近几年来高强钢越来越被广泛关注，但大多局限于构件，材料，力学方面的研究，对于梁柱节点抗震方面的研究相对较少。文献[1]中试验表明，结构的承载力和延性性能指标受节点脆性破坏的影响非常大，试件发生破坏时节点的承载力和延性指标难以满足设计要求。文献[2]对腹板螺栓连接型梁柱连接节点进行了研究，研究表明腹板螺栓对节点抗震性能有一定的提升。文献[3]进行了多组足尺节点试件试验，试验结果表明，改进型节点抗震性能普遍提高。

带加劲肋顶底角钢也是改进型节点中的其中一种，所以对此节点研究很有必要。

顶底角钢的连接是钢结构梁柱连接节点中的新型连接方式。这种连接方式相对传统连接方式而言，具有高效、简单、经济和高质量等优点。国内外对此节点进行相关试验的研究，试验表明此节点不但具有较好的变形能力而且具有较好的延性性能。但是节点承载力和初始转动刚度有所降低。国外对于该型节点的研究较早且都主要是试验研究，对于采用有限元软件进行研究分析的仍然较少。

试验研究具有一定的局限性，测量数据会存在一定的误差或者无法得到。但是采用有限元模拟可以避免以上缺陷，因此采用有限元分析具有一定的研究意义。

本文主要是对华南理工大学王鹏等试验节点采用Abaqus 6.13进行有限元模拟分析，并将Abaqus软件分析的结果与试验得出的结论进行对比研究，验证有限元软件模型的正确性，然后采用高强钢分析节点抗震性能。

1 有限元模型

试验中设计了5个梁柱角钢连接节点试件，加载方式为单调加载，其编号为SA-1、SAS-1、SAS-2、SAS-3、WAS-3；5个循环加载试件，其编号为CSA-1、CSAS-1、CSAS-2、CWAS-3、CSAS-3。采用10.9级M16摩擦型高强螺栓将梁柱节点进行连接。

为了研究各种形式节点的受力性能，确保试验节点中的柱处于弹性状态[4]，因此设计梁相对柱较弱。加劲肋、梁、角钢均采用强度等级为Q235B钢材，强轴连接时柱采用Q345B钢材，弱轴连接时柱采用Q235B钢材。试件主要参数见文献[5]，节点的基本构造见图1。

1.1 材料本构

遵循结构抗震设计中的强柱弱梁[6]的基本原则，柱钢材等级选用Q345，要比其他构件高一级，梁、加劲肋、角钢及其他钢材等级选用Q235。钢材的本构关系见图2。

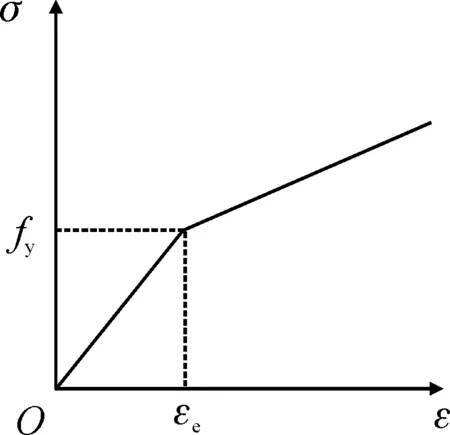
图2 本构关系图Fig.2 Constitutive relationship diagram

对于双折线模型的应力应变关系模型的数学表达式见式：

(1)

式中：σs为应力，εs为应变，εe为钢材的比例极限点对应的应变，Es为钢材的弹性模量，Et为钢材的切线模量，fy为钢材的屈服强度。

1.2 单元选取与网格划分

在梁柱节点实体模拟中，在有限元的计算中单元体的选择非常重要，三维实体单元C3D8R为八节点减缩积分单元，对于解决接触问题和网格受扭问题具有良好的效果，故本文采用这种单元对梁柱节点中各个零部件进行实体单元模拟。在单元选取中有四面体单元与六面体单元两种，四面体单元对复杂几何适应性好，但结果精度较差。相比而言，六面体单元的计算规模较小，精度较高，故本文网格划分采用六面体单元，各个部件网格划分见图3。

图3 各个部件网格划分Fig.3 Meshing of various components

1.3 材料模型

本文有限元模型分析中的钢材为型钢和钢板，试验进行之前，为了得到较为准确的材料模型，对各类钢材进行了材性试验，结果见表1。强化模型采用双线性随动强化，屈服准则采用Von Mises准则[7]。采用双线性模型来表示高强度螺栓的应力-应变关系，其钢材的屈服强度fby为970 MPa，抗拉强度fbu为1 207 MPa。所有材料模型Poisson比均为0.3，材料均为各向同性。构件采用高强钢分析时，梁柱角钢均采用Q690钢材，各材料的参数见表2。

表1 钢材材性试验结果

表2 钢材的材料性能

1.4 加载制度

有限元模型采用和试验相同的加载制度，其单调加载方式由力和位移控制加载，循环加载由层间位移角控制加载，循环加载加载制度见图4。这样的加载方式有利于变形协调。

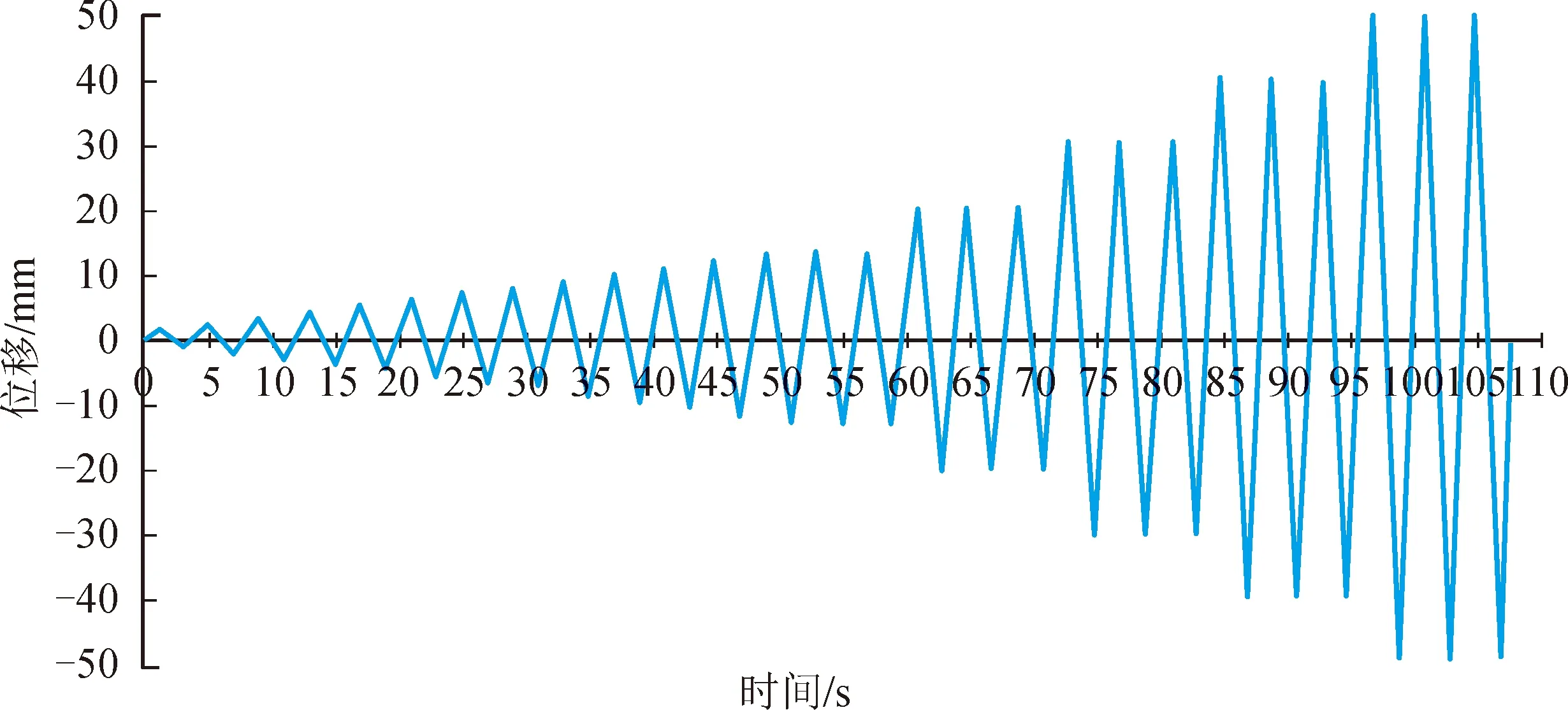
图4 位移荷载加载曲线Fig.4 Displacement load loading curve

考虑到节点的破坏形式，当位移荷载加载至层间位移角θ达3%(110 mm位移荷载)时停止加载，其中层间位移角θ是梁端脱开位移Δ与梁端到柱的中心线距离L之比，加载制度见图4。

1.5 模型验证

1.5.1试件破坏形态

为了研究试件整体变形过程，采用非线性计算分析方法对试件节点模型进行有限元分析，本文给出典型试件破坏模式变形图，破坏模式见图5。

图5 试件破坏形态Fig.5 Specimen damage form

试件SA-1在加载初期时，试件处于弹性工作阶段，试件整体没有发生变化。荷载的增长速度与位移基本一致。当荷载逐渐增加，微小缝隙开始于顶部一侧角钢根部与柱翼缘之间出现，缝隙随着荷载的增加逐渐增大，见图5(b)。加载后期，试件底角钢两者具有相似的极限变形状态。试件SAS-1，在位移荷载加载过程中，顶部一侧角钢根部、加劲肋焊接处与柱翼缘之间有随着梁端位移荷载增加而增大的间隙出现，和图5(c)～(d)两者破坏状态基本相似。试件SAS-2在加载初期，受拉一侧角钢根部与柱翼缘间有随着位移增加而增大的微小缝隙出现，加载后期，加劲肋底角钢加劲肋受压弯曲，产生平面外弯曲变形，和图5(e)～(f)两者极限变形状态基本相似。试件SAS-3，在加载初期，顶部角钢出现微小受拉变形，随着梁端位移荷载的增加，顶部角钢根部、加劲肋焊接处与柱翼缘之间有缝隙产生，且随着荷载的增加缝隙逐步增大，最终由于加劲肋处焊缝被拉断裂而停止加载，和图5(g)～(h)两者极限变形状态基本相符。试件WAS-3随着荷载的逐渐增加，角钢与腹板之间的间隙逐渐增大，随后顶部角钢出现受拉变形，当加载荷载接近峰值荷载时试件首先在顶或底角钢加劲肋附近出现细小裂纹。最终，顶角钢或底角钢上裂缝拓展至角钢根部，导致角钢一侧完全断裂，见图5(i)～(j)。

1.5.2弯矩-转角曲线

通过上述单调加载方式来模拟，可以得到节点的弯矩-转角(M-θ)曲线，见图6。

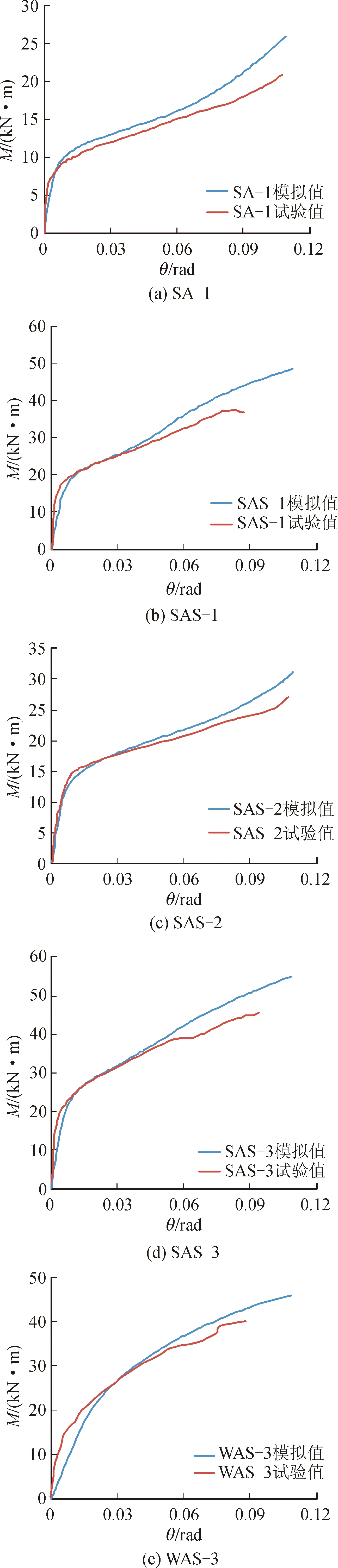
图6 弯矩-转角曲线Fig.6 Bending moment-corner curve

见图6(a)～(e)图，试件SA-1，SAS-1，SAS-2，SAS-3，WAS-3有限元模拟的弯矩转角曲线和试验弯矩转角曲线大致相同，屈服点的位置相差不大，都有向上走的趋势，有限元模拟数据和试验数据基本吻合，从而验证了有限元模型的有效性。

参考文献[8-10]，为方便归一化处理，把节点塑性受弯承载力MPK定义为曲线初始阶段切线与后屈服阶段切线的交点，单调试验主要结果见表3。

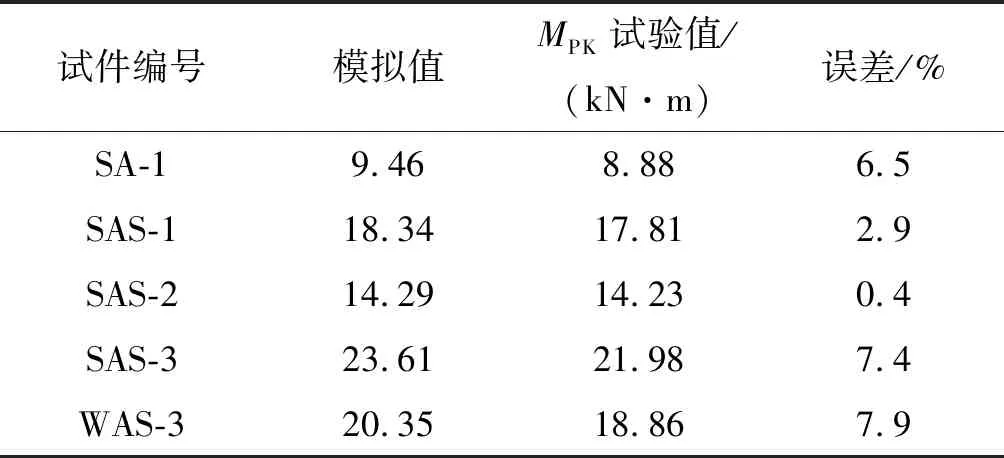
表3 承载力试验值与模拟值比较

对表3数据结果进行分析可得，试件SA-1与试件SAS-1有限元模拟结果的塑性受弯承载力相差93.87%，试件SA-1与试件SAS-2的塑性受弯承载力相差51.06%，可见增设顶角钢加劲肋提高节点的塑性受弯承载力显著增强。表3中五个试件塑性受弯承载力结果中模拟值与试验值平均误差约为5%，说明所建立的有限元模型良好。试验值与模拟值的对比分析为后续高强钢分析奠定了基础。

2 高强钢结果分析

2.1 滞回曲线

模型在力循环往复作用下，得到的结构抗力与变形之间的关系曲线称为滞回曲线[11]。试件加载过程中节点处的最大弯矩值为Mmax，在最大弯矩Mmax作用下的梁柱相对转角为θmax。同时取破坏弯矩Md=0.85Mmax，与之对应的极限转角为θu。为了方便进行归一化处理，将弯矩M与梁的全截面塑性弯矩Mbp的比值作为滞回曲线的竖轴。对应特征点结果见表4，五组试件的滞回曲线见图7。

表4 循环加载试验结果

图7 试件滞回曲线Fig.7 Specimen hysteresis curve

由图7知上述构件全部用高强钢承载力明显提高。由图7(b)～(d)可见，三个构件在达到最大承载力之前，滞回曲线较饱满呈纺锤形。加载初期滞回曲线呈线性变化，卸载时发生很小的残余变形，刚度基本不退化，此时耗能能力很小。随着荷载增加，滞回曲线不再呈直线变化而逐渐呈纺锤形。逐级加载过程中，节点峰值荷载不断减小，节点强度不断退化。滞回曲线所包的面积略有减小，刚度退化略有明显。三个构件可见，图7(d)滞回曲线极限承载能力较大，说明增设顶底角钢加劲肋对结构影响较大。相对于图7(b)～(c)两图，只增设顶加劲肋或底加劲肋对构件承载能力提高较为明显。

由表4可知，试件CSA-1采用高强钢Q690比普通钢承载力提高32%，体现出高强钢使用增强构件受弯承载力，在顶底角钢均设有加劲肋受弯承载力最大，对应梁柱相对转角最小，体现了加劲肋对节点的重要性。

2.2 骨架曲线

把滞回曲线上每一个循环加载的峰值点连成一条平滑曲线，称为模型的骨架曲线[12]，试件的骨架曲线见图8。

由图8可得:峰值弯矩和破坏弯矩分别在增设顶底角钢加劲肋之后增加1倍，而顶底角钢同时增设加劲肋之后峰值弯矩和破坏弯矩显著增强。对比普通钢Q235钢材峰值弯矩，破坏弯矩增加了30%左右。

2.3 耗能

构件的耗能能力可以用等效粘滞阻尼系数he来进行分析，he越大说明构件的耗能能力越强，he可以按图7中滞回曲线的最外一圈ABCD与横轴围成的图形面积A1和三角形△BOC的面积A2之和的比值来确定。

结构抗震的重要性能指标是节点的滞回耗能能力[13]，抗震性能的优劣取决于节点耗散和吸收能量的能力。结构吸收能量是在试件加载过程中进行，而耗散能量是在卸载过程中进行，两者之间的差值称为“耗散能量”，即结构在一个循环荷载作用下的耗能能力。耗能能力代表了一个滞回环的饱满程度，滞回环越饱满，耗能能力越好。能量耗散系数Ce是评定结构耗能能力的重要指标，本文通过计算每一个滞回环包围的面积来反映试件耗散能量的能力。能量耗散系数计算公式为：

(2)

图8 试件骨架曲线Fig.8 Specimen skeleton curve

式(2)中ABC和CDA是指滞回曲线与横轴所围的区域，见图9。本文通过Origin8.0软件计算每个滞回环体的面积。

图9 耗能系数确定Fig.9 Energy consumption coefficient determination

通过分析可得，试件破坏时的耗能系数为2.30，表明此类节点耗能性能良好。

2.4 节点刚性与延性

在结构设计中，刚度反映了结构抵抗变形的能力，在工程实际中，刚度在外在荷载因素作用下会发生一定程度的改变，而这种变化被称为刚度退化[14]，刚度退化也是试件抗震性能的一个重要指标，因此研究试件的刚度退化变得尤为重要。在地震作用下，刚度的大小对结构所受实际震害有至关重要的作用，一般刚度大的结构吸收能量较少，故破坏危害比较严重，而刚度较小的结构具有较大的弹塑性变形来释放所吸收的地震能量，故破坏危害相对轻微，耐震性能要比刚度大的结构好。所以刚度的大小对结构耗能能力起着关键性作用。

结构的延性[15]是指结构在荷载作用下从屈服开始至达到最大承载力或达到以后还具有足够塑性变形的能力。为了避免结构发生脆性破坏，结构要具备一定的延性特征，通常用转角延性系数来衡量延性特征。其计算公式为：

(3)

式中：θm为节点转动能力，节点的转动能力按骨架曲线中转角的最大值；θy为节点受弯承载力对应转角，也称之为弹性极限弯矩转角。试件极限弯矩转角见表5。

表5 延性指标

由表5可知，试件CSA-1的转角延性系数为36而增设上下顶底角钢加劲肋的试件CSAS-3的转角延性系数下降为23.03，说明同时增设上下顶底角钢加劲肋有助于增加节点延性，对于加劲肋顶底角钢连接节点延性系数μθ为23.03～36。通过分析可得，此类节点具有相对较好的延性，满足抗震设计的要求。

3 结 论

1) 有限元模拟得到的试件受弯承载力与试验值基本相同，平均误差约为5%。因此有限元模型较为准确。

2) 高强度钢材节点具有较好的塑性承载能力，其塑性承载力比普通Q345B钢材至少提高32%左右。

3) 不论高强钢还是普通钢，顶底角钢连接节点同时增设加劲肋后，承载力均会增强。

4) 顶底角钢连接节点同时增设加劲肋后，滞回曲线相对饱满，与无加劲肋角钢连接节点对比节点的耗能能力显著增强。

5) 同时增设上下顶底角钢加劲肋有助于增加节点延性，对于加劲肋顶底角钢连接节点延性系数μθ为23.03～36。因此此类节点具有相对较好的延性，满足抗震设计的要求。