基于模糊聚类的可重构制造工艺规划方法

王永泉，张广鹏，张 倩

(1. 西安理工大学 机械与精密仪器工程学院，陕西 西安 710048；2. 湖北汽车工业学院 机械工程学院，湖北 十堰 442002)

可重构制造(reconfigurable manufacturing, RM)是面向批量加工行业所提出的一种新的制造模式，它能有效解决批量加工中高效、低成本与生产柔性之间的矛盾[1]。合理构建可重构制造系统(reconfigurable manufacturing system, RMS)是实现可重构制造的关键，可重构机床(reconfigurable machine tools, RMT)是构成RMS的基础，通过RMT可实现零件族内各零件的加工转换[2]，而被加工零件的加工工艺方案直接影响RMT功能模块群的配置与重构方案的选择，故研究面向可重构制造的零件族工艺方案规划方法将对RMT及RMS的合理设计具有重要意义[3]。

目前，国内外对可重构制造系统、机床模块化设计已有广泛的研究[4-11]，而面向可重构制造的零件族工艺方案规划方法的研究并不多，这也是RMS研究中的瓶颈问题之一。大多数研究主要侧重于以节省成本、提高产能为目的，对现有生产线进行优化研究[12-15]，面向可重构制造提出了一些较宏观的工艺创成方法[16-17]。但RMT的设计与RMS工艺密切相关[1]，目前仍缺乏将二者密切结合的设计研究，这给RMS实际应用验证带来困难[18]。

文献[19]基于所提出的工序单元、工序段概念，将RMT设计与可重构制造工艺设计相关联，为可重构制造工艺创成提供了新思路。但经多次验证后发现，该方法对具有较复杂结构的零件群进行工艺规划时会产生海量冗余数据，因而会给计算机自动处理带来困难。

本文在上述方法的基础上，经加工顺序排列形成“工序单元序列”、“工序段序列”，并据此经多层次模糊聚类分析，创成零件族可重构制造工艺方案。以某汽车变速箱体零件族加工为例，经验证，该方法有效避免了工艺方案规划中海量冗余信息的处理问题，为更加高效地获取复杂零件族合理可行的工艺方案提供了方法。

1 零件加工信息矩阵

首先要根据被加工零件的加工要求，明确设计基准，确定被加工特征的工艺基准，提取出所有加工信息，形成零件加工信息矩阵，作为工艺方案制定的基础依据。本文采用n×14矩阵来描述加工信息，n表示加工特征总数；某一零件的加工特征信息用Ci(i=1, 2, …,n)表示，Ci中包含14种加工信息，即Ci={ci,0,ci,1,…,ci,13}，其中，零件加工特征的自然序号为ci,0；方位代码为ci,1，ci,1可取值Ⅰ，Ⅱ，…，Ⅶ，以分别表示六个方位及斜向方位；特征类型代码为ci,2；工序类型为ci,3；加工特征的定位基准为ci,4、ci,5、ci,6；加工特征在总体坐标系中的坐标值为ci,7、ci,8、ci,9；采用多轴箱时对应的最小主轴孔径为ci,10；在本加工特征之前必须完成的加工特征序号为ci,11(亦称“加工顺序号”)；同源加工特征编号为ci,12，在同源加工特征中的顺序号则为ci,13。

所谓“同源加工特征”是由最终加工特征溯源得到的系列相关加工特征，同源加工特征具有明确的加工顺序。例如，大孔的加工工艺过程若为“粗镗孔”、“半精镗孔”、“精镗孔”，则该孔的同源加工特征可通过最终加工特征依次溯源，其加工顺序分别为：“粗镗孔”、“半精镗孔”、“精镗孔”。

2 工序单元序列的生成

一个工序单元的加工特征可通过一个多轴箱或一个主轴头来完成，故一个工序单元对应零件某一方位的加工内容。因此，要由前述得到的零件加工信息矩阵，对零件各加工方位的所有加工特征进行判别、合并处理，形成对应方位的工序单元。本文分两步进行，即先生成自然合并工序单元，再生成各方位工序单元及工序单元序列。

2.1 自然合并工序单元

根据所填写的加工信息矩阵，通过检索方式将零件的同方位、同类型、同加工基准、无加工顺序冲突的加工特征进行自然合并，形成“自然合并工序单元”(简称“自然工序单元”)。若采用多轴箱加工，这些自然合并的加工特征不但要有共同的进给速度允许区间，还需满足多轴箱加工的最小主轴间距等条件。用以上方法得到的自然工序单元方案可能有很多，本文以包含加工特征最多的原则形成自然工序单元，这样可以减少RMT数量。

2.2 工序单元及工序单元序列

对同一方位自然工序单元组配形成该方位的工序单元。为了得到所有可能的工序单元，需要对自然工序单元通过检索方式遍历组配，即每个自然工序单元可独立成为一个工序单元，也可两个组配、三个组配或多个组配等，在组配过程中，通过约束条件检验，将符合条件者保留，形成备选工序单元方案。组配的约束条件包括：加工顺序要求、具有相似的加工特征(如面、孔加工分开)、加工基准相容原则[19]。采用多轴箱加工时，各自然工序单元具有共同的进给速度区间以及满足最小主轴间距等条件，如图1所示。

图1 某一方位组配生成工序单元过程示意图Fig.1 Generating process diagram of the process units of a part in a machining direction

最后将包含零件某方位所有加工特征且加工特征不重复的工序单元筛选出来，组合形成一个工序单元序列，这样可以得到很多工序单元序列方案(见图1)。

2.3 工序单元顺序矩阵

每一工序单元序列中，各工序单元之间的加工顺序关系可用一个矩阵来描述，称之为“工序单元顺序矩阵”，该矩阵的行元素和列元素都为工序单元序列中的各工序单元，用工序单元数字编号来表示。矩阵赋值规则为：行元素若在列元素之前加工，则对应的矩阵项赋值为“1”，否则为“0”，工序单元间的加工顺序关系可由它们所包含的加工特征顺序号由加工顺序溯源方式来获取。

3 工序段序列的形成

一个工序段对应一台RMT的加工内容，因此需要将各方位的工序单元进行组配以形成工序段的加工内容。

为便于描述，先建立零件加工方位坐标系，图2用编号描述零件的六个加工方位，若该零件的六个方位都要加工，与专机加工生产线一样，RMT可采用多刀或多主轴头并行加工。广义上一台RMT并行加工的方位可取五个(第六方位作为固定面)、四个、三个、两个或一个，每种情况下可能有多种组合形式，故可选的工序段方案可能有很多。

图2 零件的加工方位面描述Fig.2 Description of the processing directions of the part

工序段是将各方位的工序单元组配后形成的，因此工序段中的工序单元应满足3个约束条件：①同一工序段中的工序单元应具有相同的加工基准，以保证工件一次装夹即可完成各方位工序单元的加工；②满足总体加工顺序要求，即工序段中的各工序单元加工顺序无冲突，可通过检索方式，从工序单元顺序矩阵中获取顺序信息；③孔加工特征与面加工特征分属不同的工序段，以保证工序段中各工序单元互不干扰。

工序段的生成步骤为：首先将各方位工序单元序列中的工序单元依据工序单元顺序矩阵，重新按顺序排列形成新的“工序单元序列”；参照前述各方位工序单元顺序矩阵的形成方法，将参与组配的所有方位工序单元用一个工序单元顺序矩阵来描述工序单元间的顺序关系；然后依据前述工序段形成的3个约束条件，将各方位的工序单元序列中的工序单元进行组配形成工序段。由于组配方案可能有很多种，为了减少RMT配置的数量，本文将尽可能多的工序单元组配到一个工序段中，这样可以减少RMT数量。因前述零件加工方位组合有很多种，每种组合下都可得到多种工序段组配方案，每一组配方案即形成一个“工序段序列”。

4 基于模糊聚类分析的可重构制造相似工艺方案确定

面向零件族的可重构制造工艺方案创成。可重构制造的目标是找出零件族中各零件间最相似的工艺方案，以保证可重构制造系统在加工不同零件时能快速转换。前已述及，在工序单元序列及工序段序列的形成过程中，会产生大量的可选方案，导致信息太多，难以快速找到相似工艺方案，为此本文采用三层模糊聚类法找出零件族中的相似工艺方案：

①按零件并行加工方位组合次序，通过模糊聚类进行零件间工序单元序列的相似性分析，选出最为相似的工序单元序列进行交叉组配，形成工序段方案，即工序段序列；

②对得到的各零件工序段序列(按加工顺序排布)，再进行模糊聚类相似性分析，选出零件间最为相似的工序段序列；

③以工序单元顺序矩阵为依据，将各零件相似的面加工与孔加工工序段序列排列生成各自的加工工艺方案，对这些工艺方案再进行模糊聚类相似性分析，得到零件间最相似的工艺方案，以此作为可重构机床设计和方案重构的依据。

图3为族内两零件采用两个并行加工方位组合，经模糊聚类相似性分析，生成两零件相似工序段序列方案的过程示意图，其中A1、A2、…、An，B1、B2、…、Bm以及K1、K2、…、Kn，L1、L2、…、Lm表示工序单元序列中的各工序单元，C1、C2、…、Ci，D1、D2、…、Dj表示工序段序列中的各工序段。

图3 两零件采用两个并行加工方位面组合分别形成工序段序列过程示意图Fig.3 Forming process diagram of the sequential process sections of two parts machined concurrently in two directions respectively

以下简要介绍本文所采用的多层次模糊聚类相似性分析数学模型。设论域U={x1,x2,…,xj,…,xn}(j=1, 2, …,n)为被分类的对象，每个对象又由m个指标表示其性状，即xj={xj1,xj2,…,xjk,…,xjm}(k=1, 2, …,m)。这里模糊聚类所考虑的相似性特征因素包括加工特征的类型、数量及其加工次序。

例如建立零件族某一方位孔系工序单元序列的聚类分析原始信息数据矩阵X=(xjk)n×m，其中n为要比较的工序单元序列总数量，m为所含的相似性加工特征信息总数。Xjk表示第j个工序单元序列中按加工顺序排列的第k个孔加工特征数据指标，它有两种数据类型，其一为加工特征类型数据指标，即按加工顺序，若存在特指的某种加工特征类型，其数值设为1(否则为0)，其二为相应加工特征的数量。为了使不同量纲的量也能比较，由于xjk≥0，在无需变换的条件下，可直接采用数量积法建立模糊相似矩阵R=(rjs)n×n，有：

(1)

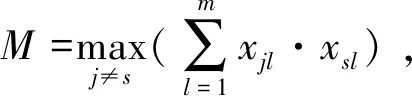
5 应用举例

以某汽车变速箱体零件族(箱体类零件)的加工为例，利用本文方法进行零件族可重构制造工艺方案规划。

5.1 零件加工特征分析

图4为由两个零件组成的某汽车变速箱体零件族，首先按照两零件的特征相似性将它们置于同一坐标系下，根据零件族加工特点，对两零件的对应加工方位进行编号，再找出所有可能的并行加工方位组合。该汽车变速箱体零件族的特点是：族内零件都有两个窗口面(即方位Ⅳ、Ⅴ)相对，两个大端面(即方位Ⅱ、Ⅲ)相对，而结合面(即方位Ⅰ)往往作为加工时的定位面和支撑面，方位Ⅵ无加工特征。该零件族采用大结合面“一面两销”定位加工，该特征需作为基准面先行加工。本例采用多轴箱加工。

图4 某汽车变速箱体零件族Fig.4 Part family of auto gearbox housing

5.2 工艺方案创成

1) 建立加工信息矩阵，如表1、2所示，两零件分别有142条和139条加工特征信息，限于篇幅，表中仅列出部分信息。

2) 自然工序单元。首先检索零件加工特征信息矩阵，将零件同方位、同类型、加工基准相同、满足多轴箱加工最小主轴间距条件(孔系加工)、无加工顺序冲突的加工特征进行自然合并，再按包含加工特征数量最多的原则，建立各零件的自然工序单元。两零件最终得到的自然工序单元方案各有一套。

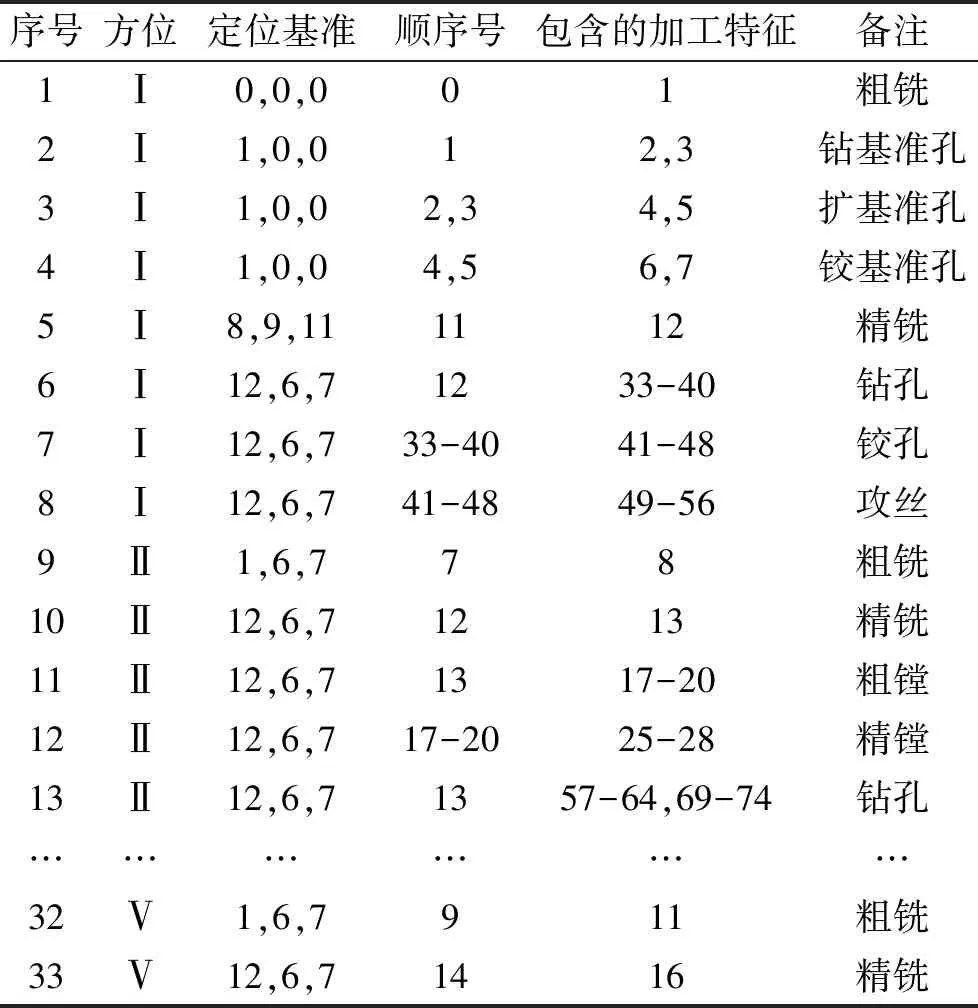
3) 工序单元及工序单元序列。按照前述检索组配方法及约束条件检验，由自然工序单元生成两零件的工序单元，如表3、表4所示的零件1与零件2分别有32和33个工序单元。经过对工序单元的筛选组合得到工序单元序列，两零件各有一种。

4) 工序单元顺序矩阵。表3、表4中两零件工序单元的顺序号(即加工特征编号)表示该工序单元加工之前必须完成的系列加工特征，根据这些顺序号及各工序单元所含加工特征编号，经加工顺序溯源，追溯出各方位所有工序单元序列中工序单元之间的加工顺序关系，生成零件的工序单元顺序矩阵。限于篇幅，本文仅列出了零件1的Ⅰ、Ⅱ方位工序单元顺序矩阵，如矩阵A、B所示：

以矩阵A中第一行第二列元素为例，“1”表示工序单元1的加工顺序位于工序单元2之前，否则为“0”；矩阵B同理。

再依据各方位工序单元顺序矩阵合并形成零件的工序单元顺序矩阵来对后续生成的工序段序列和工艺方案进行校验，限于篇幅，本文仅列出了零件1的工序单元顺序矩阵C。

C=

5) 工序段及工序段序列。先将各方位工序单元序列中的工序单元依据工序单元顺序矩阵，按先后顺序排列形成新的“工序单元序列”，再选取由2个到5个不等的并行加工方位组合，按照前述的工序段生成原则，生成各方位组合下的工序段方案。由于可选的方位组合数量多，限于篇幅，基于模糊聚类分析以零件{Ⅰ，Ⅱ，Ⅲ}和{Ⅳ，Ⅴ}两种方位组合为例，介绍工序段及工序段序列的生成过程。

先以孔加工工序单元序列的相似性分析为例进行介绍。①两零件方位Ⅰ所生成的工序单元序列各有1个。②两零件方位Ⅱ生成的工序单元序列数量分别为10个和15个，将两零件的这25个序列按顺序从1到25重新编号，按加工顺序提取它们所含加工特征的类型(包括钻、扩、…、精镗)、数量信息作为相似性分析的特征因素，形成聚类分析的原始信息数据表，如表5所示。经模糊聚类后，由聚类图5(a)可以看出，零件1的工序单元序列5与零件2的序列16、17、18、19最为相似，其相似度为0.757 1。③两零件方位Ⅲ生成的工序单元序列数量分别为10个和15个，由聚类图5(b) 所示，零件1的序列2、5分别与零件2的序列22、19最为相似，其相似度为0.997 1。④两零件方位Ⅳ生成的工序单元序列数量分别为1个和10个，由聚类图5(c)所示，零件1的序列1与零件2的序列5最为相似，其相似度为0.991 1。⑤零件1方位Ⅴ的工序单元序列仅1种，零件2的方位Ⅴ无孔加工。

以{Ⅰ，Ⅱ，Ⅲ}方位组合为例，基于前述两零件各方位面最为相似的工序单元序列，先将零件1方位Ⅱ与方位Ⅲ的工序单元序列进行交叉组配，经工序单元顺序矩阵校验，剔除不符合顺序的工序段序列。同样，将零件2方位Ⅱ与方位Ⅲ的工序单元序列进行组配和顺序校验，获得满足顺序的工序段序列。再对两零件Ⅱ、Ⅲ方位组合下得到的工序段序列重新编号、聚类后，得到零件1的工序段序列1与零件2的工序段序列5最为相似，其相似度为0.999 1，如图5(d)所示。最后将两零件方位Ⅰ的工序单元序列再融入到上述获得的工序段序列中进行组配，经顺序校验，生成{Ⅰ，Ⅱ，Ⅲ}方位组合下两零件的工序段序列。对这些工序段序列再经编号、聚类后，得到零件1的工序段序列9与零件2的工序段序列22、24、25最为相似，其相似度为0.983 7，如图5(e)所示。

类似地，可以生成另一方位组合{Ⅳ，Ⅴ}下两零件相似的工序段序列方案，这里不再赘述。

表1 零件1的加工信息矩阵

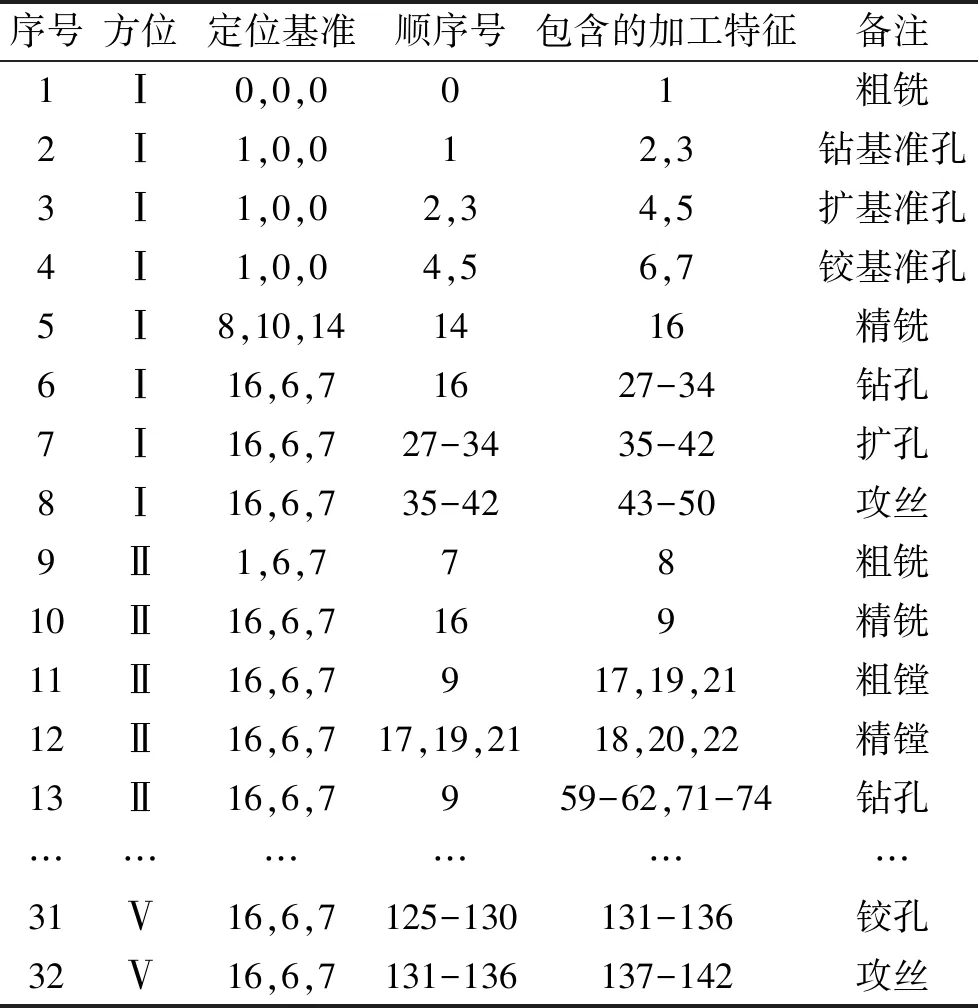
表3 零件1的工序单元信息表

表4 零件2的工序单元信息表

Tab.4 Information table of process units of Part 2

序号方位定位基准顺序号包含的加工特征备注1Ⅰ0,0,001粗铣2Ⅰ1,0,012,3钻基准孔3Ⅰ1,0,02,34,5扩基准孔4Ⅰ1,0,04,56,7铰基准孔5Ⅰ8,9,111112精铣6Ⅰ12,6,71233-40钻孔7Ⅰ12,6,733-4041-48铰孔8Ⅰ12,6,741-4849-56攻丝9Ⅱ1,6,778粗铣10Ⅱ12,6,71213精铣11Ⅱ12,6,71317-20粗镗12Ⅱ12,6,717-2025-28精镗13Ⅱ12,6,71357-64,69-74钻孔………………32Ⅴ1,6,7911粗铣33Ⅴ12,6,71416精铣

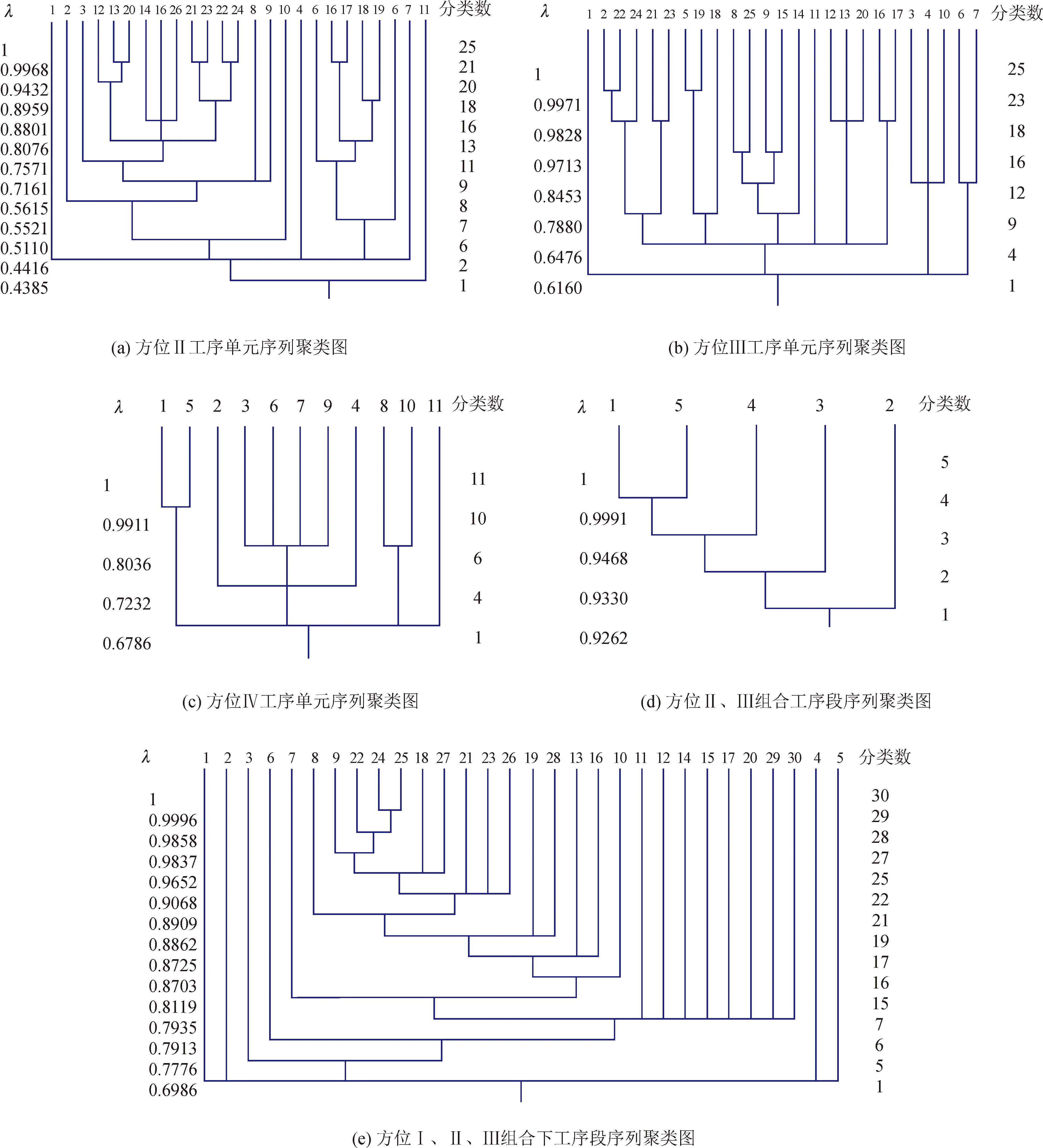
图5 两零件工序单元序列及工序段序列的聚类图Fig.5 Clustering trees of sequential process units, and sequential process sections of two parts

最后，将{Ⅰ，Ⅱ，Ⅲ}、{Ⅳ，Ⅴ}两种方位组合下得到的两零件最为相似的孔加工工序段序列分别进行穿插排列、加工顺序校验，得到两零件孔加工工艺方案，零件1有56种，零件2有1 680种。

6) 同样的方法，可以得到两零件最为相似的8种面加工工艺方案。

7) 对前述得到的两零件所有方位组合下孔加工与面加工工艺方案分别进行穿插排列、加工顺序校验，可获得零件1的224种工艺方案和零件2的6 720种工艺方案。

对两零件的这些工艺方案再进行模糊聚类相似性分析，经重新编号和聚类分析后，零件1的工艺方案16、20、23、8、22、6、7分别与零件2相对应的工艺方案64、69、72、(59，61)、(70，73)、55、57最为相似，相似度都为0.975 0。限于篇幅，图6仅列出两零件部分工艺方案的聚类分析结果。

仅分析两零件第1组相似的工艺方案，即：

零件1的第16工艺方案：

1-2-3-4-(9,16)-(23,28)-5-(10,17)-(24,29)-(25,30)-(11,18)-(13,6,20)-(12,19)-(26,31)-(21,32)-(14,7,21)-(15,8,22)

零件2的第64工艺方案：

1-2-3-4-(9,17)-(25,32)-5-(10,18)-(26,33)-(19,11)-27-(21,13,6)-(22,14)-28-29-(23,15,7)-(24,16,8)-(20,12)-30-31。

上述工艺方案中“-”两侧为各工序段，数字表示该工序段中工序单元编号；“()”表示括号中的工序可合并为一道工序。两零件的上述两工艺方案的加工特征信息如表6所示。由该表从宏观上可以看出，两工艺方案所对应工序段中的加工特征类型及其数量、加工特征的加工顺序排列、加工方位组合具有极大的相似性，所以当两零件在进行加工转换时，所需的可重构机床变换模块数量最少，能有效解决大批量定制生产中高效、低成本与生产柔性之间的矛盾。

6 结 论

针对文献[19]方法进行复杂零件工艺方案规划时所出现的海量冗余数据难以处理的问题，本文研究了基于模糊聚类多层次分析的可重构制造工艺规划方法，并举例验证了其可行性。

1) 通过建立零件族加工方位坐标系，以加工方位分类组合方式将工序单元组配成工序单元序列，再用模糊聚类相似性分析获得零件族各方位相似度较高的工序单元序列，解决了第一层工序单元方案海量信息问题。

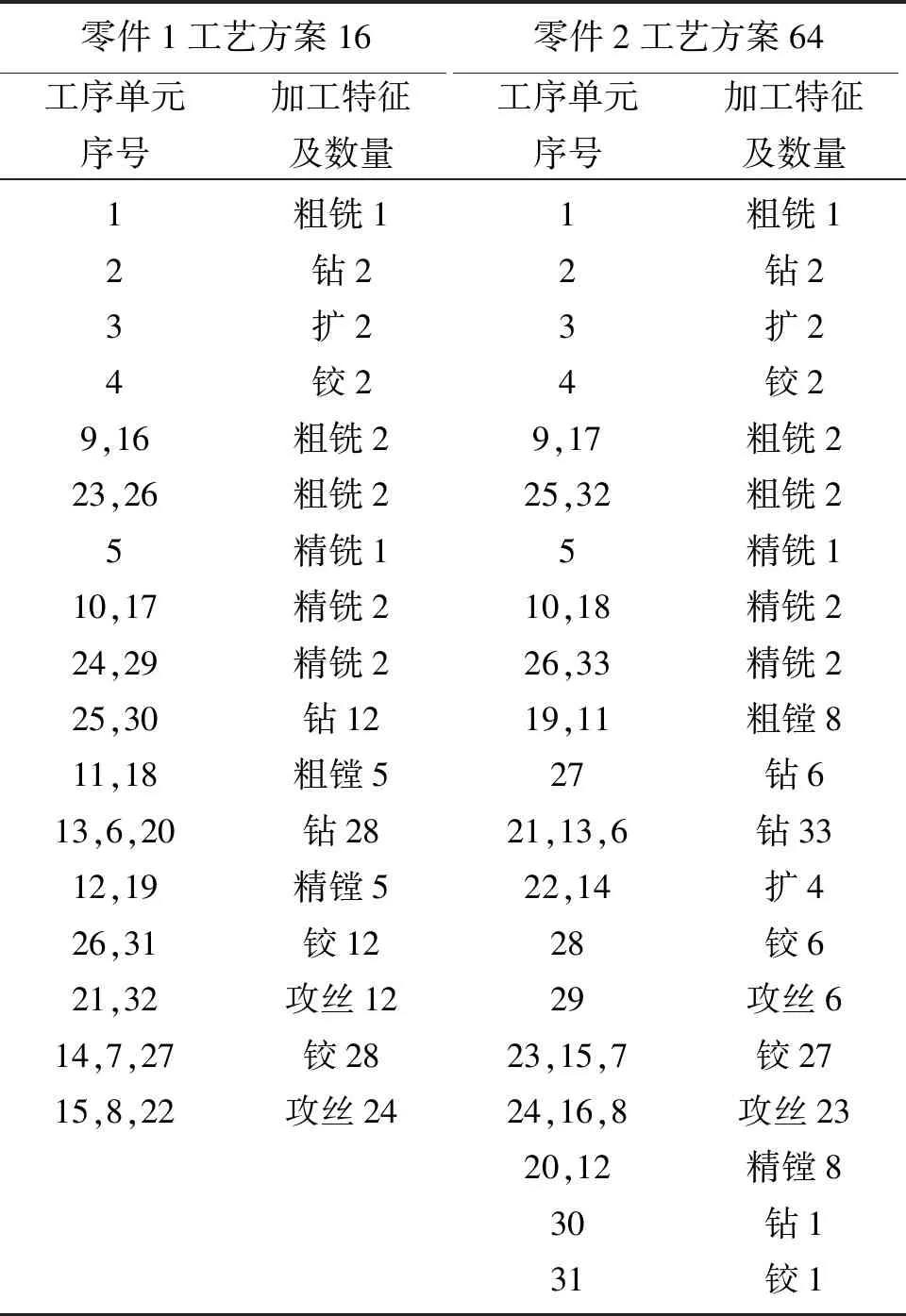
表6 零件1与零件2一组相似加工工艺方案的比较

2) 以零件族各方位具有相似特征的工序单元序列为基础，通过交叉组配及工艺顺序校验，筛出不同方位组合条件下的工序段序列方案，再以模糊聚类相似性分析得到具有相似性的工序段序列方案，解决了第二层工序段方案海量信息问题。

3) 依据零件的工序单元顺序矩阵，将箱体类零件的面加工和孔加工工序段序列排列组合成备选工艺方案，然后以模糊聚类相似性分析得到零件间最相似的工艺方案，解决了第三层工艺方案海量信息问题。