导体材料涡流热成像应力检测的仿真

(四川大学 制造科学与工程学院，成都 610065)

工业零部件在生产、加工及使用过程中，会受到外部载荷的作用，从而在材料的局部区域产生应力集中，致使材料的力学性能降低，甚至导致材料失效。因此，对材料或结构的应力状态进行检测与监测，特别是采用无损检测方法进行检测与监测是很有必要的。在众多的无损检测方法中，涡流热成像检测(ECT)技术可以快速地检测试件表面或近表面的缺陷，如表面裂纹[1-3]、腐蚀缺陷[4-6]、焊接缺陷[7-9]、疲劳损伤[10-12]等。同超声法、射线法等相比，ECT方法具有非接触、单次检测面积大、对复杂形状零件的易适应性等优点，可用于大范围内的应力先验检测。近几年，不少专家学者将涡流热成像检测技术应用于金属材料冲击损伤应力、拉伸应力的检测中，并取得了一定的研究成果。通过检测多次冲击后的钢板，刘录叶等证明了应用ECT检测冲击残余应力是可行的[13]；利用ECT检测拉伸应力，有学者给出了材料纵向和横向电磁特性的变化规律[14]以及应力和热导率之间的线性耦合关系[15]；雷庆等有效定量了单向拉伸载荷下钢结构的表面应力[16]等。但在实际应力检测中，预制一定量大小及分布厚度的应力样本试件比较困难，结果量化也比较复杂。因此，笔者采用数值仿真分析手段，通过设置材料局部区域的电导率、热导率等参数的大小及其厚度来模拟实际应力层，建立涡流热成像仿真模型并分析试件表面温度响应的变化情况，试图为涡流热成像定量检测材料或结构的应力提供理论参考。

1 ECT应力检测原理

应用ECT技术检测导体材料的应力分布时，含应力区域的感应涡流密度大小是异于正常区域的，且与应力幅值相关，应力幅值的改变会导致材料电磁特性参数和传热特性参数的改变，从而使得感应焦耳热在材料内部传导的速度发生改变，最终表现为热成像图像温度场的不均匀分布和应力区与非应力区的温升变化规律的不一致。通过对ECT热成像图像/序列的后期处理分析，可以获得材料的应力状态，其检测理论模型如图1所示。电导率变化主要影响检测过程中的感应加热，热导率主要影响冷却过程中的热传导。

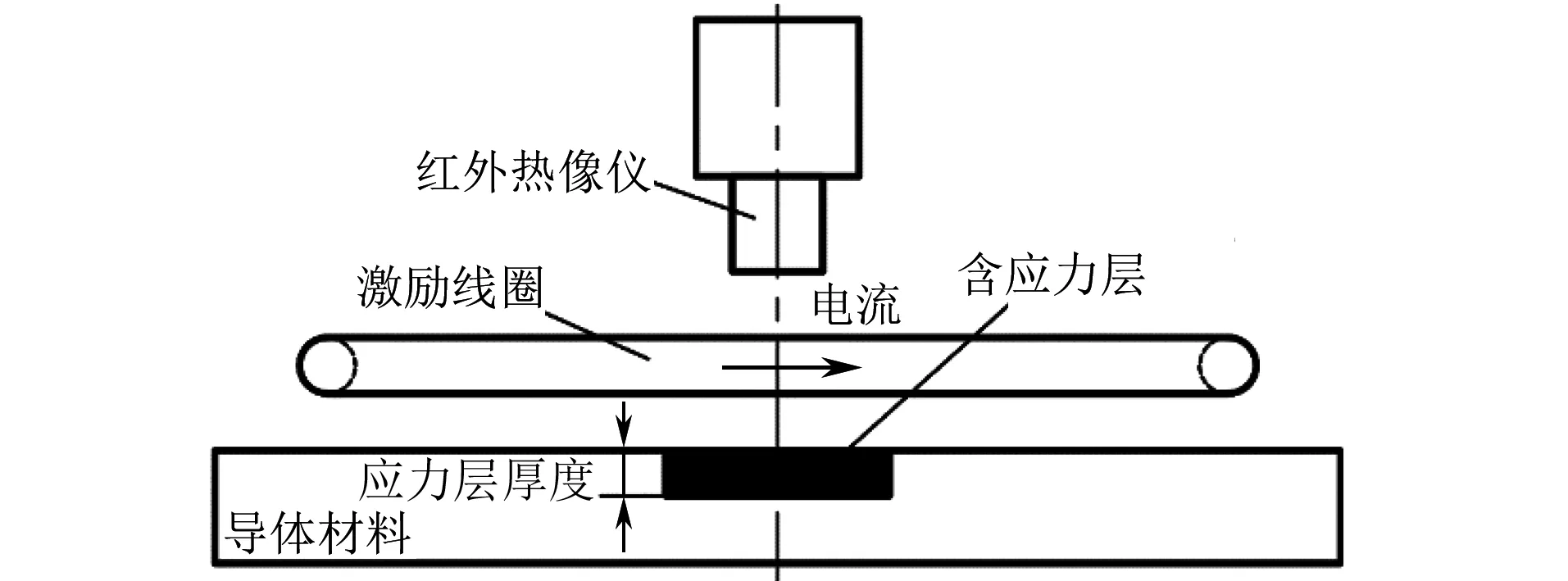
图1 ECT应力检测理论模型

1.1 检测原理

涡流热成像技术在检测过程中所涉及到的物理过程有：感应涡流加热、热传导、红外辐射[17]。当激励线圈中通有一定频率的交变电流时，会产生电磁感应现象，即在被测导体内会感应出相同频率的电涡流，由麦克斯韦尔方程推导出该涡流场的控制方程如式(1)所示。

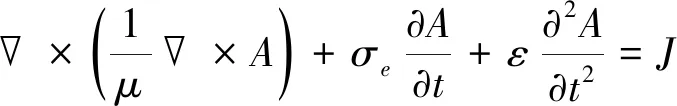
(1)

式中：μ为材料的磁导率；A为磁矢势；σe为材料的电导率；ε为介电常数；J为外部电流密度;t为电磁激励作用时间。

产生的涡流会产生集肤效应，积聚在被测导体表面，其集肤深度dJ的计算公式如式(2)所示。

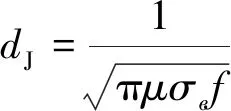
(2)

式中：f为激励电流频率。

由焦耳定律可知，部分涡流会在导体内部由电能转换为热能，产生的焦耳热Q正比于涡流密度Js和电场强度E，其计算公式如式(3)所示。

(3)

由式(3)可知，影响焦耳热的因素主要有导体材料的电导率和涡流密度，但因为电导率也会影响涡流的密度值，因此焦耳热与电导率不是单纯的负幂次关系，其变化规律还需要进一步探讨。

在感应加热阶段产生的焦耳热Q会在被测试件内部进行传递，其传递规律及热扩散深度dT的计算公式如式(4)，(5)所示。

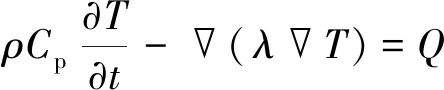
(4)

(5)

式中：ρ为材料密度；Cp为材料的比热容；T为材料热力学温度；λ为材料的热导率；α=λ/(ρCp)为导体热扩散系数;t为热扩散的时间。

1.2 应力对导体材料属性的影响

1.2.1 金属电阻应变效应

导体材料内部应力会使得材料内部原子间的距离和点阵的动畸变发生变化，导致材料的电阻率发生变化，从而影响材料的电导率[15，18]。一般情况下，电导率随应力的变化呈负指数关系，当指数的绝对值远远小于1时，则略去高阶小项，近似成为线性关系。其影响规律遵循式(6)[19]。

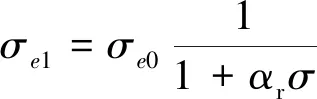
(6)

式中：σe1为导体存在应力时的电导率；σe0为导体无应力时的电导率；σ为应力值(拉应力为正、压应力为负)；αr为应力系数。

即当试件存在拉应力时，其应力区域的电导率将减小相反，当试件存在压应力时，其应力区域的电导率将增大。

在检测过程中，由于被测试件产生的焦耳热会影响材料本身的温度，且电导率会随温度的变化而发生变化，其关系遵循式(7)。

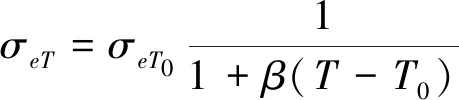
(7)

式中：σeT，σeT0分别为材料在温度T，T0时的电导率；β为导体电阻温度系数。

1.2.2 魏德曼-弗兰兹定律

由魏德曼-弗兰兹定律可知，在室温下很多金属的热导率与电导率之比几乎相同，如式(8)所示。因此当被测试件内部存在应力时，应力区域的热导率也会随着电导率的改变而发生相应改变。

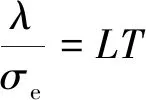
(8)

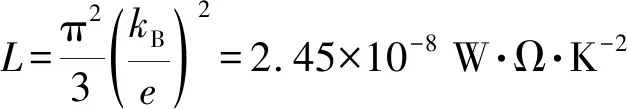
设λ0为无应力时的热导率，λ1为存在应力时的热导率。设置仿真模型参数时，同电导率一样，当试件存在拉应力时，将试件应力区域的热导率λ1同σe1等比例减小；相反，当试件存在压应力时，将λ1同σe1等比例增大。

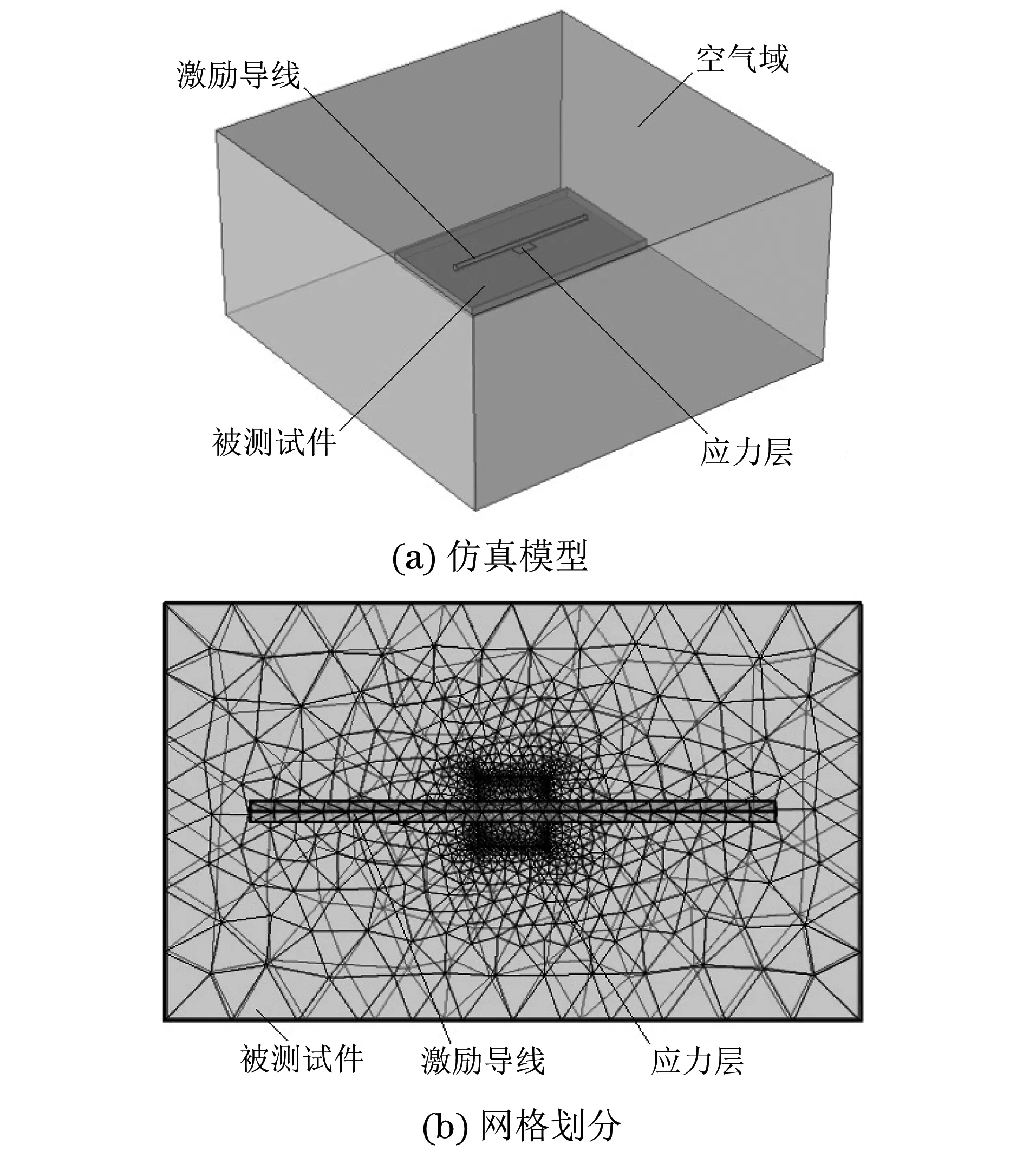
图2 涡流热成像检测的仿真模型及其网格划分

2 ECT应力检测仿真模型

涡流热成像检测过程中，被测试件温升的热源主要来自导体材料的电磁损耗，在进行数值仿真分析时，需要耦合电磁场和温度场。文章用COMSOL MUTIPHYSICS多物理仿真软件建立了脉冲涡流热成像检测的三维模型，模型及其网格划分如图2所示。选取电磁场与热传导两个物理场进行耦合，并将热传导模式设置为固体传热，通过瞬态分析获取激励加热阶段和自然冷却阶段的温度场变化情况。激励线圈直径为6 mm，长150 mm，距检测表面的提离为1 mm；导体材料的尺寸(长×宽×厚)为200 mm×120 mm×10 mm，中部存在(长×宽)20 mm×20 mm的区域为电导率及热导率变化层，厚度可变，模拟被测试件存在应力的区域；初始温度设置为293 K，激励电流设置为500 A，加载频率为250 kHz，加热时间为500 ms，冷却时间为1 000 ms，即总的检测时间为1 500 ms。

仿真所用导体材料的参数见表1，由式(5)计算出材料正常区域在检测结束后的热扩散深度可达到4.231 mm，即在研究应力层厚度对温度响应曲线的影响时，最大厚度不能超过4.231 mm。

表1 仿真所用材料的参数

3 COMSOL仿真结果讨论

在分析仿真结果的过程中，分别考查被测导体表面点1(位于试件应力层中部)和点2(位于远离应力层的正常区域处)的温度响应变化情况。如图3所示，点1,点2的检测值分别代表应力层及远离应力层的正常区域的表面温度值，以下曲线原始数据点均是基于点1,点2处的温度值所绘制。

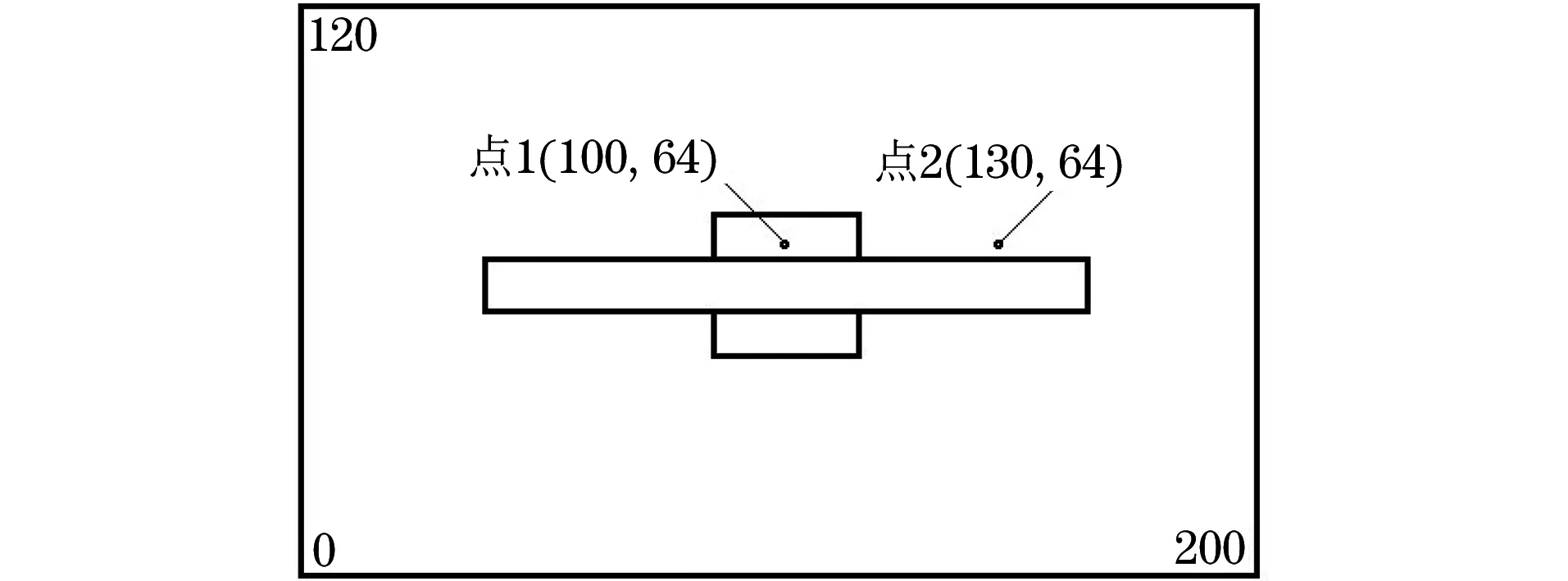
图3 数据取点位置示意

3.1 电导率、热导率变化与检测结果的关系

电导率、热导率变化层即所模拟的应力层，其厚度设置为1 mm，导体正常区域的电导率σe0设置为5.0×106S·m-1，为得到较光滑的仿真曲线，应力区域的电导率σe1设置如下：从1.0×105S·m-1以1.0×105S·m-1的增量逐次增加至5.0×106S·m-1，模拟拉应力层；再继续从5.0×106S·m-1以1.0×105S·m-1的增量逐次增加至1.0×107S·m-1，模拟压应力层。其中，热导率与电导率呈等比例变化，因此后续结果分析中只列出了电导率与温度值的关系。结合仿真结果，探讨上述变化过程中被测试件表面温升曲线的响应情况。改变层电导率对导体表面温度分布的影响如图4所示。

图4 改变层电导率对导体表面温度分布的影响

图5 不同电导率对应点1,点2处的温度响应曲线

由图4可见，被测导体拉应力层区域的温度明显高于标准件的，且拉应力越大，应力层感应涡流越集中，加热结束及冷却结束时的高温区越明显；相反，压应力层区域的温度低于标准件的，压应力越大，应力层感应涡流越分散，低温区范围越大。不同电导率对应点1，点2处的温度响应曲线如图5所示，可以看出电导率的改变对点1处的温度影响较大，基于此可评估应力大小的变化情况，而远离应力区域的点2处温度几乎不受电导率变化影响，可以其作为拉、压应力层温度的参照值。

图6 加热结束时电导率变化对点1、点2处温度值的影响

图6是应力区域点1处与正常区域点2处在加热结束时的温度T1,T2随电导率、热导率变化的曲线图，从图中可以看出，拉应力层电导率越小，应力区温度高于正常区且温差越大；压应力层电导率越大，应力区温度低于正常区且温差也越大。通过式(6)反演导体电导率与其应力绝对值(不考虑拉、压应力的正负问题)之间的关系，如式(9)所示，并绘制应力大小变化与点1、点2处温度差值(T1-T2)之间的关系曲线图，如图7所示。

(9)

图7 应力变化对温度的影响

结果表明，在一定范围内，导体应力值与表面应力区域和正常区域的温度差近似为线性关系。拉应力越大，应力区与正常区的正温差越大；压应力越大，应力区与正常区的负温差越大。

3.2 应力层厚度变化与检测结果的关系

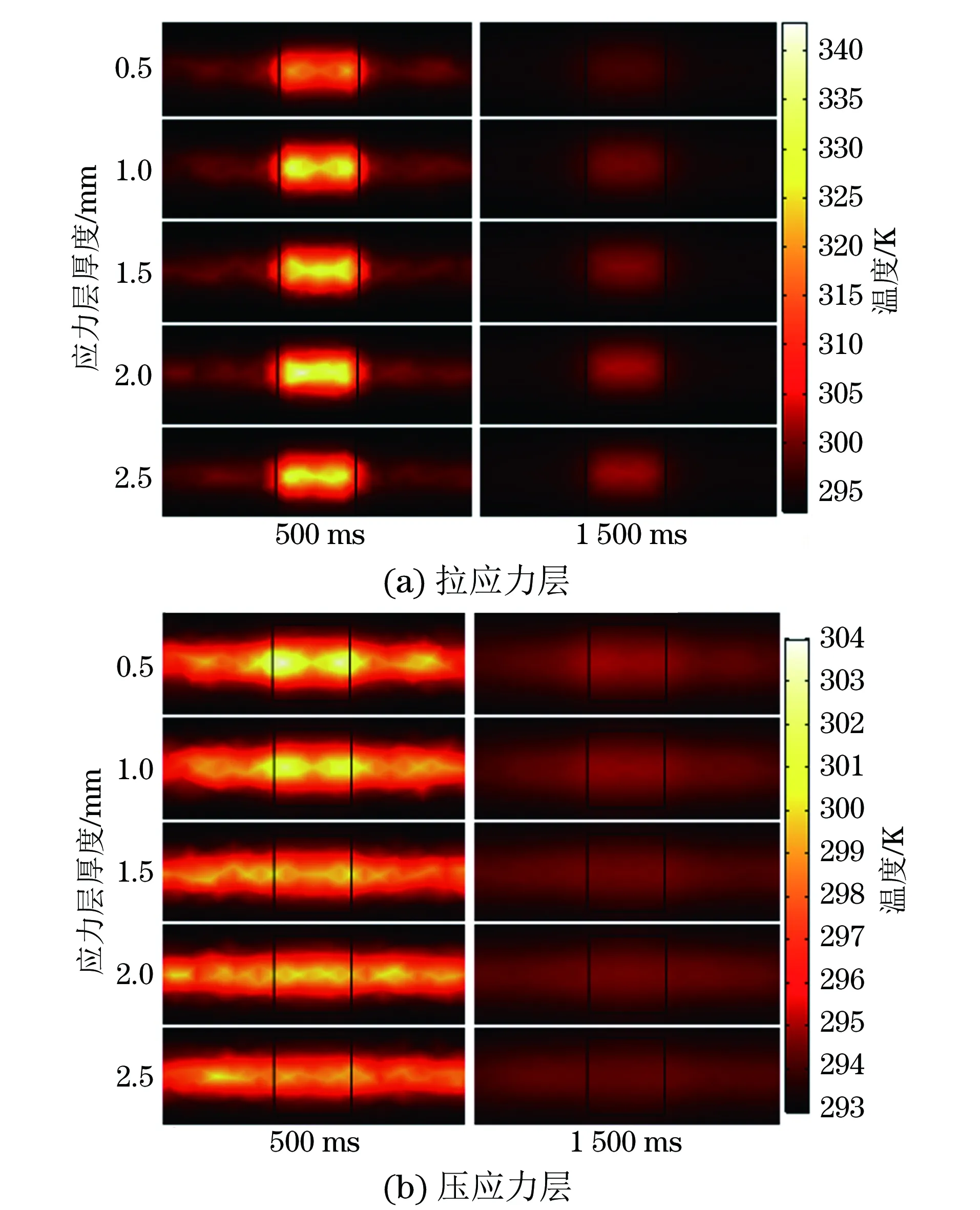
图8 应力层厚度变化对导体表面温度分布的影响

类比裂纹缺陷深度的影响，研究导体应力层的厚度改变时，其表面温度响应曲线的变化规律,正常区域、拉应力层以及压应力层的电导率分别设置为5.0×106,2.0×106,8.0×106S·m-1。则由式(5)可计算得到冷却阶段结束时模拟拉、压应力层的热扩散深度分别为2.68,5.35 mm。因此，模拟应力层的厚度不能超过2.68 mm。在仿真分析时，将最大应力层厚度设置为2.5 mm，应力层厚度从0.5 mm开始,以0.1 mm为增量逐渐叠加。应力层厚度变化对导体表面温度分布的影响如图8所示。

由图8可见，拉应力层厚度越大时，靠近应力区的感应涡流越多、越集中，因此应力层表面温度分布越集中，最大温度值越大；相反，压应力层厚度增大时，感应涡流逐渐向正常区域靠近，应力层表面温度分布越分散，最大温度值越小。对应应力层厚度变化时，在加热结束及冷却结束时点1处的温度值均相应发生变化，如图9所示。因此可以通过导体应力层表面温度的变化来反演应力层的厚度值。

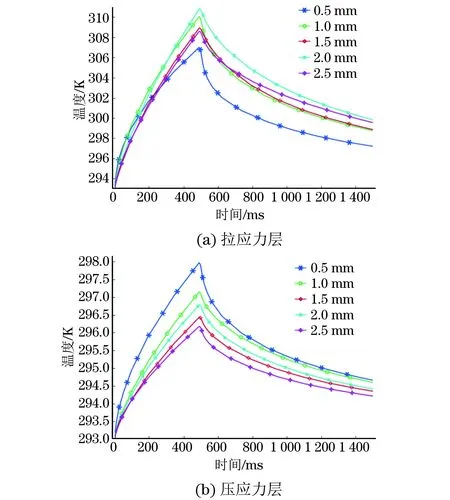
图9 不同应力层厚度对应点1处的温度响应曲线

图10 应力层厚度对点1处温度值的影响

由图8,9可以看出，拉应力层在冷却阶段结束时的温度随厚度的变化明显，而压应力层在加热结束时的温度随厚度的变化明显，在加热结束时模拟压应力层的热扩散深度已达到3.1 mm，大于最大厚度2.5 mm，因此后续探究应力层厚度与温度变化之间的关系时，拉应力选取冷却阶段结束时的数据，压应力层选取加热结束时的数据。应力层厚度对点1处温度值的影响如图10所示，导体应力区域应力层厚度与表面温度近似为线性函数关系。拉应力层厚度越大，其表面温度就越高；压应力层厚度越大，其表面温度就越低。

4 结论

讨论了涡流热成像法检测应力的原理，建立了数值仿真模型，利用多物理场耦合的有限元方法，分析了导体应力层厚度及电导率、热导率大小变化对表面不同区域点的温度响应曲线的影响，根据仿真结果，给出了应力大小及应力层厚度变化与温度之间的关系。

(1) 在一定范围内，导体应力值与其表面检测温度近似为线性关系，即可以通过导体表面各点的温度变化情况反演得到导体表面应力的大小。若导体表面存在拉应力，则应力区的温度将高于正常区的，且拉应力越大，应力层的温度越高；若导体表面存在压应力，则应力区的温度将低于正常区的，且压应力越大，应力层的温度越低。

(2) 在已知应力值大小的条件下，导体应力层厚度与其表面检测温度近似为线性函数关系，拉应力层越厚，对应表面温度越高；压应力层越厚，对应表面温度越低。即可以通过温度值的大小来分别确定拉、压应力层厚度。