基于互联网+的新型不定线公交策略研究*

韩冬成 赵 欣 李 旸

(武汉理工大学交通学院1) 武汉 430063) (海信网络科技2) 青岛 266071)

0 引 言

地方政府大力支持公共交通的发展，采取公交专用道、交叉口公交优先等先进的管理措施，提高了公交车在路段和交叉口处的通行效率，增强了公共交通的吸引力.但随着公交规模扩大和乘客需求的增加，系统内部运行出现了公交列车化现象和公交站点拥堵等问题，形成了新的交通瓶颈点.

此外，公交系统的资源没有得到充分利用.很多公交线路过长，沿线的公交停靠站较多，同时沿线部分公交站点乘客数量不均，即使某站点没有乘客，公交车也会照常停靠.同时，在交通量较大的地段，公交站点有大量的公交车停靠，增加了路段的负荷，加剧了拥堵.部分公交线路为了一个或几个公交站而选择了绕线行驶，甚至有些公交线路形成了多个环形，大大增加了公交车的运行时间.

Leiva等[1-5]在公交车变线运行的基础上，针对不同的公交线路，分析公交跳站运行对乘客出行的影响，建立了以公交乘客出行时间最小为目标的优化模型，分析不同的车次分别跳站的运行效果.不定线公交优化策略建立了不同的公交变线模型，对公交乘客和公交公司的成本等因素做了研究，但影响了公交系统的可靠性，公交车行驶信息的滞后性造成乘客无法及时了解公交车的通行路径.互联网技术的发展将给传统的交通运输业带来新的变化.

1 互联网及传统公交特性分析对比

互联网技术、思维或者模式等在传统行业的应用即为互联网+[6]，“互联网+公共交通”的发展模式给城市公交系统的未来发展指明了方向.两者的结合能够带给公共交通新的特点：乘客乘车信息的实时性、乘客乘车信息及公交车信息的双向传递、乘客乘车大数据的获取.

传统公交与互联网+公交特性相比，在公交的路径、站点、信息等方面存在着显著的不同，见表1.

2 基于原线路站点的动态公交

2.1 模式介绍及分析

基于原线路站点的动态公交模式包括两方面：①允许公交车跳站运行 在原线路的基础上，基于实时的乘客需求，允许公交车跳过一些公交站点.需要注意的是该趟公交车在跳过某一站后，下一趟公交车不一定会跳过该站.跳过的站点不确定，将按照当时的车上乘客、等车乘客人数等因素，建立公交跳站模型判断跳过哪些公交站.同时规定站点有乘客下车时必须停车.②新型不定线公交 基于原线路对路径做适当调整.由于公交车运行时可以跳过公交站，则当公交车跳过某站时，可以选择新的不经过该公交站的路径行驶，即选择通过时间最短的路径，当路径与公交车原有路径不同时，公交车可以改变行驶路径.

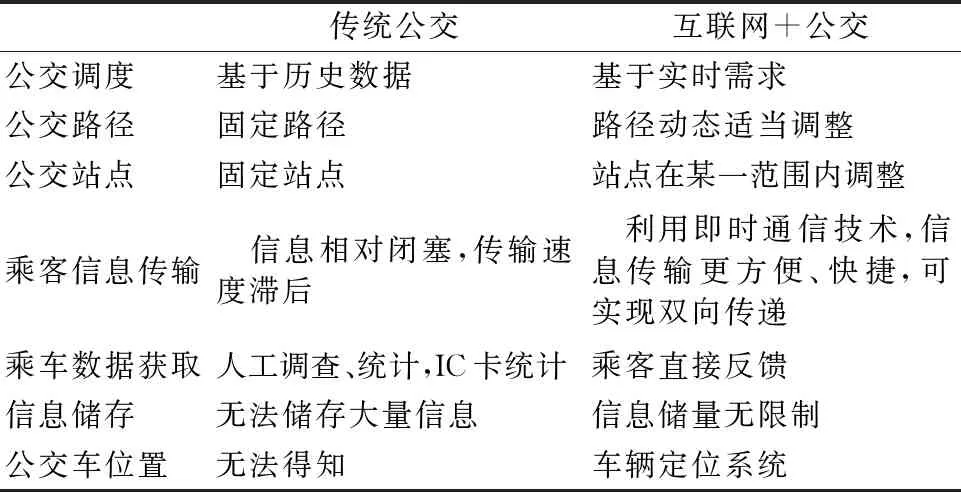
表1 传统公交与互联网+公交对比

该模式可以提高公交系统的运行效率.公交车行驶过程中，会遇到部分车站没有人上下车，公交车跳过当前时刻没有人上下车或者上车人数相对很少的站点可以节省公交车的通行时间，为了便于讨论，假设车辆跳过站点后，乘客会继续在该站等车；此外公交车在跳站后选择通行时间更短的路径行驶，可以进一步减少通行时间，提高公交效率.但是，该模式会增加部分乘客的等车时间.考虑在公交车跳站模型中引入跳过站点后乘客多等待的时间，将这部分时间作为跳站判断的重要因素.

2.2 乘客到达站点分布研究

国内外学者对公交乘客的到站分布已有居多研究，认为乘客的到站符合泊松分布[7].以武汉市公交909路关山大道关南小区站、关山大道华夏学院站和大学园路化徐村三站进行乘客数量调查.见表2.

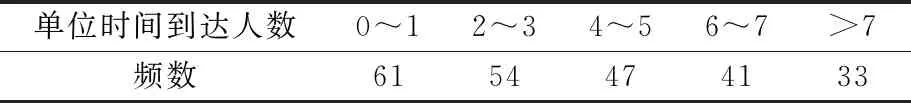
表2 乘客到达人数

利用SPSS软件，对到达人数进行分析可以发现，对乘客到达数进行的泊松分布检验中，渐进显著性为0.967，大于0.5，即乘客到达站点服从泊松分布.

2.3 公交最优路径选择

当公交车跳过了某一个站点时，公交车会选择从当前站点到下一停靠站的最优路径行驶.由于公交车跳站运行的过程中，跳过站点后到下一个站点距离较短，路况复杂程度不高，故最优路径的选择通过Dijkstra(迪杰斯特拉)算法进行计算.

2.4 公交跳站模型

公交跳站运行过程中，公交车内乘客的总出行时间成本下降，而公交站点处等车乘客的出行时间成本增加.公交跳站模型则以乘客站点总出行时间最小为目标函数，求解公交车跳站情况.

乘客站点总出行时间成本T.

α·Ni·tsi+β·Ni·tri)

(1)

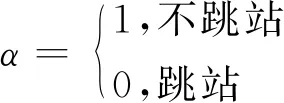
(2)

(3)

n≥0;N≥0;m≥2

式中：m为公交站点数量；ni为站点i的等车乘客数量，人；Ni为车辆到达站点i时车上乘客数量，人；tdi为站点i处乘客等车时间，s；twi为跳过站点i处乘客额外等车时间，s；tsi为车辆不跳过站点i时的过站时间，s；tri为跳过站点i并沿新路径行驶过站时间，s；w为等车时间权重；α，β为模型参数.

设公交车总共跳过了m1个公交站点，没有跳过的站点数量为m2，则总的站点出行时间为

(4)

站点出行时间主要包括乘客在公交站点等候的时间和公交车途经该公交站的运行时间两部分.而当公交车跳过站点时，乘客的站点等车时间会发生变化，当公交跳过该公交站后，等车时间增加了twi.过站行驶时间同样分跳站与不跳站，跳过公交站时其过站时间为路段行驶时间tri，而不跳站，过站时间tsi包括行驶时间、车辆减速加速时间、站点停靠时间等.为了方便乘客出行，规定当站点有乘客要下车时，公交车必须停.

2.4.1车辆过站时间

2.4.1.1 公交车不跳站时的过站时间

公交车正常运行过程中，驶过公交站点有3个部分：①路段行驶；②减速进站、加速离站；③乘客上下车.

1) 路段行驶时，路段行驶时间t1为

(5)

式中：L1为原路段长度，m；v1为路段平均行驶速度，m/s.

2) 车辆减速进站、加速离站 假设公交车的启动加速度和制动加速度同为a，减速进站和加速驶离的过程所需的时间tb为

(6)

则在减速进站和加速驶离的时间为2tb，总共行驶的距离s为

(7)

驶过同一距离，不停车需要的时间tn为

(8)

即行驶同一段距离，速度不变时花费的时间是速度变化的50%.当在路段中忽略车站长度时，可以将tb理解为公交车速度变化产生的时间成本.

3) 乘客上下车时间 除了公交车进出站点的时间外，乘客上下车的过程同样产生时间成本td，公交车在公交站点停靠时，存在两部分时间：乘客上下车时间和开关车门时间，两部分共同组成公交车停站时间td.

td=bn+toc

(9)

式中：b为单位乘客上车所需的时间，s；n为等车乘客数，人；toc为开关车门所需要的时间，s.

而开关门时间toc数值见表3.

表3 开门时间参数表 s

得到公交车不跳过公交站的过站时间tsi

(10)

2.4.1.2 跳站后的车辆过站时间

当公交车跳过站点后，沿新的路段行驶，其过站时间tri为

(11)

式中：L2为新路段长度，m；v2为车辆行驶速度，m/s.

2.4.2乘客等车时间

2.4.2.1 公交站点乘客等车时间

在公交车跳过公交站后，该站的等车乘客的时间成本被迫增加.由于，公交乘客到达公交站服从泊松分布，此时，乘客相继到达的间隔时间服从负指数分布[8].即乘客在相邻两车时间间隔内随机到达的概率密度函数为

f(t)=λe-λt

(12)

式中：λ为某公交站单位时间内乘客的到达率，人/s.

那么乘客的等车时间的期望值tdi为

(13)

式中：λ为某公交站单位时间内乘客的到达率，人/s；h为公交车的到达时间间隔，s.

2.4.2.2 跳过站点后乘客增加的等车时间

车辆跳过公交站点，站点乘客等车时间twi增加，设公交车的发车间隔时间为h，则理想情况下，乘客需要至少多等待h.

twi=h

(14)

公共交通的出行时间由到达站点的时间、等待时间、换乘时间(有换乘时)、车内时间和离开站点到达目的地时间构成，且各阶段出行时间价值根据出行者心理感知不同而变化.国外学者对公交出行各阶段时间的权重及价值进行了较为广泛的研究.Mcknight[9]根据四个国家17项研究的成果，进一步研究等待时闻价值和车内时间价值的关系，得到平均等待时间价值是车内时间价值的2.4倍.而杨晓庆[10]研究了公交乘客出行的时间价值，得到等车时间的时间价值是车内时间的1.9倍，文中取w=1.9.

公交线路的终点站乘客到达率为0，且规定终点站不可被跳过.此外，公交线路中的最后几站由于上车乘客的到达率很低，接近于0，多次被跳过后乘客的累积效果不明显.为了避免线路部分公交站被无限次的跳过，设置公交站点被连续跳过的次数不超过3次，当某一个站点被连续跳过了3次，那么第4辆公交车必须经过该站点.

2.5 模型分析

2.5.1线路站点利用率

线路站点利用率是有乘客上下车的站点占公交线路站点数的比例.不同的城市公交线路，乘客沿线的上下车情况不同，可能存在部分线路，几乎所有站点都有乘客上下车，站点利用率较高；而有些线路则有一部分站点很少有人上下车，站点利用率低.而文中将上车乘客和下车乘客分别作讨论.根据沿线站点利用率情况，将公交线路分为四类.类型1：上车、下车乘客站点利用率均高；类型2：上车乘客利用率低、下车乘客利用率高；类型3：上车乘客利用率高、下车乘客利用率低；类型4：上车、下车乘客利用率均低.

针对不同类型模拟给出沿线各站的乘客上下车人数.模拟某一条公交线路见图1.该公交线路共有22个公交站.路线全长13 km，非直线系数为1.6. 针对该路网，将公交线路沿线途经的路段和周边的路段做编号，共93段路段.用Matlab随机生成路段的车辆行驶速度，速度范围10～40 km/h.公交车到达间隔为300 s，车辆加速度为1 m/s2.

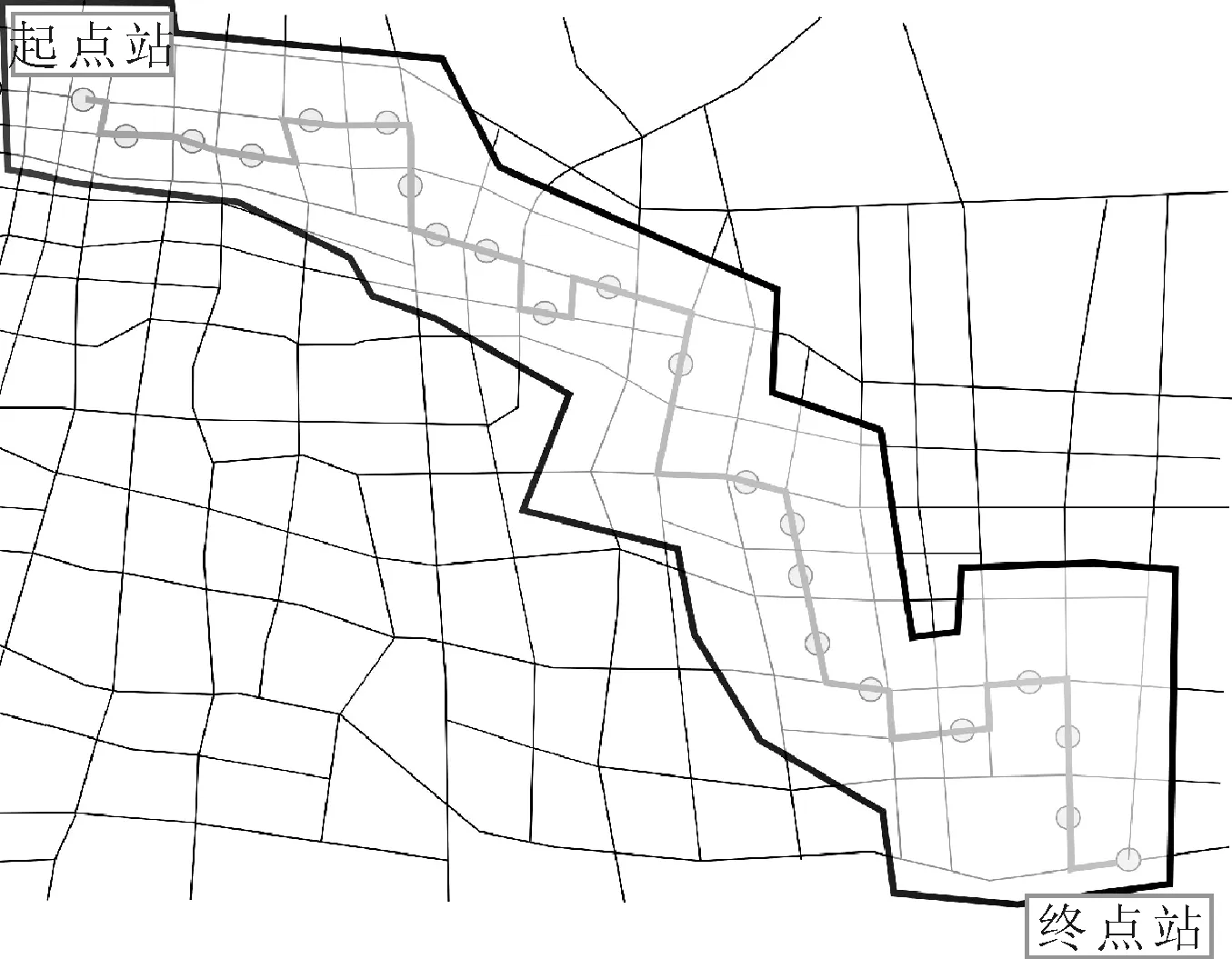
图1 公交线路及路段编号范围

根据这93段路的路段长度和路段行驶速度.使用遗传算法，求解公交跳站模型，使用dj算法求解最优路径选择，流程图见图2.取迭代次数为500次，交叉概率0.9，变异概率0.01，种群规模为22.

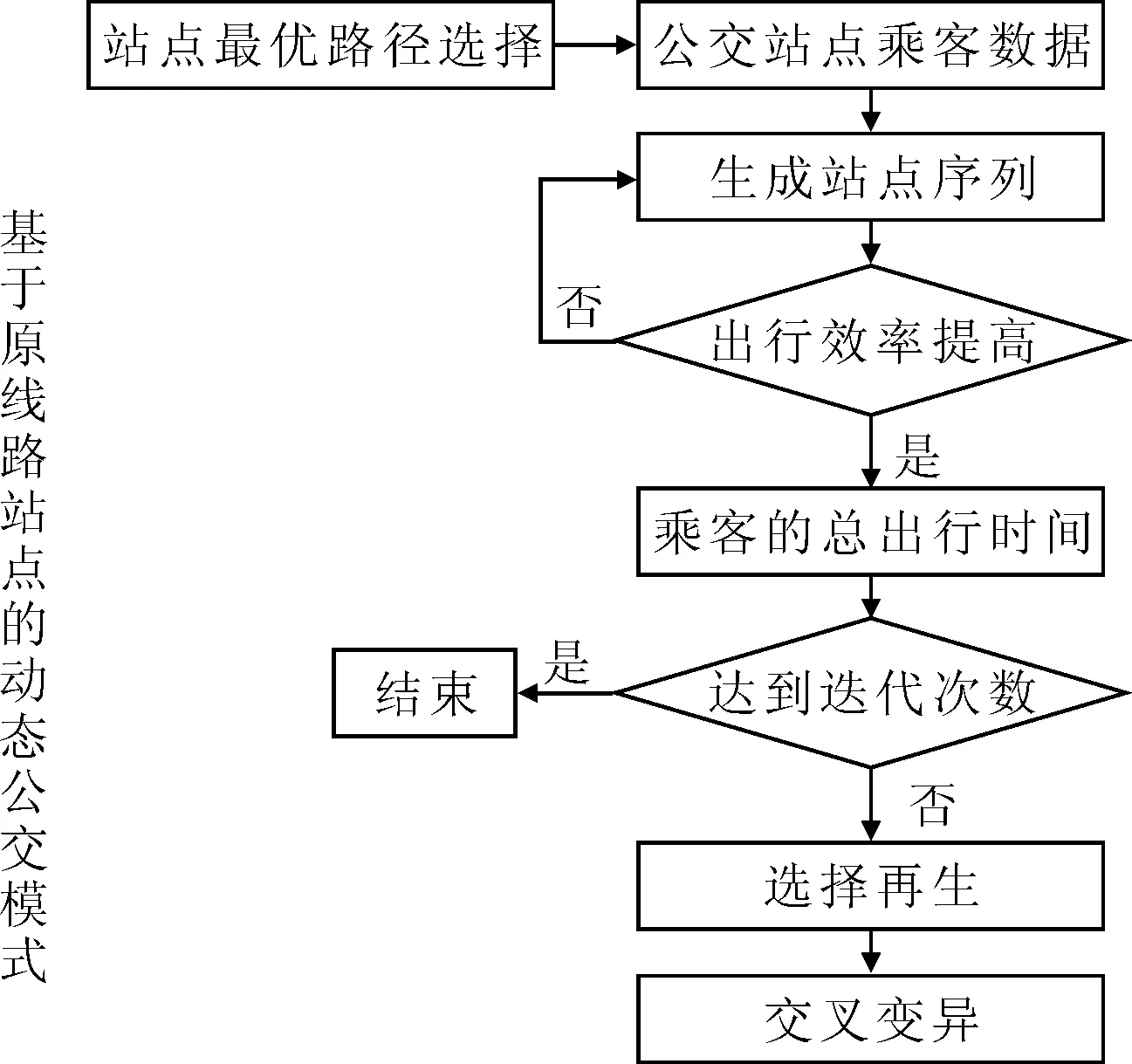
图2 模型求解流程图

分别计算不同的类型能够跳过的公交站，值得注意的是，为了方便公交车乘客下车，规定当在某公交站有乘客下车需求时，公交车必须停车.计算类型一，见图3.

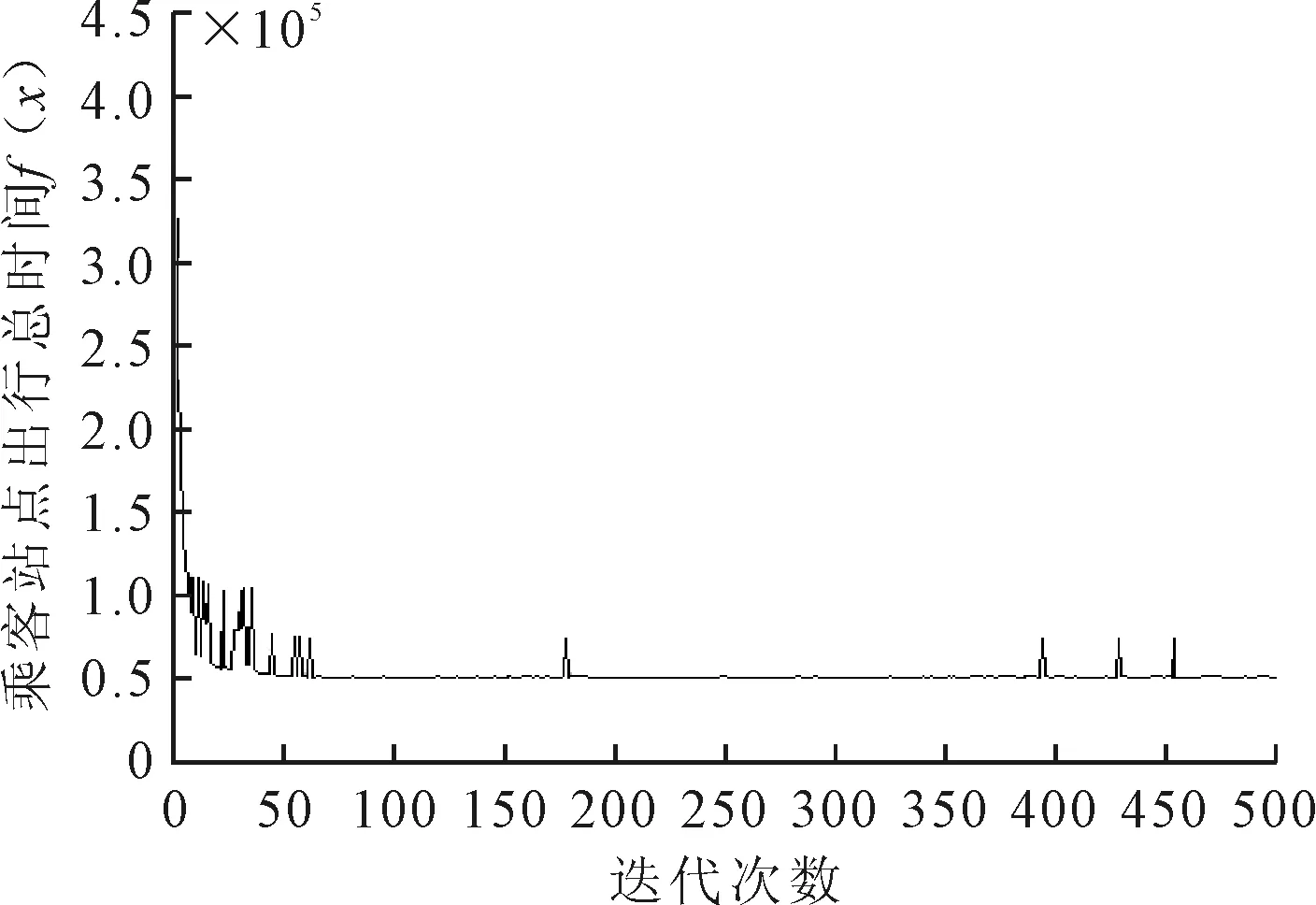
图3 乘客出行时间成本变化趋势注：横轴-迭代次数；纵轴-乘客站点出行总时间.

通过的公交站点情况：1-2-3-4-6-7-8-9-10-11-12-13-14-15-16-17-18-19-20-21-22.即只跳过了站点5.站点5上车乘客数为1，无人下车.

同理可计算在不同类型下公交车的跳站情况，汇总后见表4.

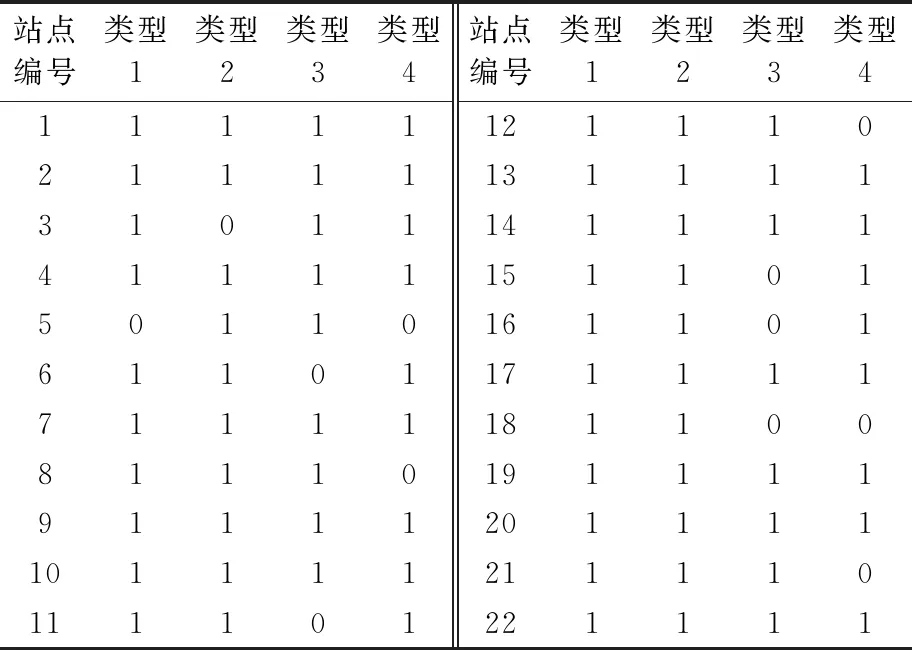
表4 公交车跳站情况

注：1-停车；0-不停车.

由表4可知，当公交车沿线站点利用率对跳站情况有明显的影响.类型1中，跳过公交站5，总的通行时间为：48 068.11 s.而不跳过公交站5，通行时间为48 649.51 s，减少了1.2%.类型2中，跳过站点3的总通行时间为49 328.98 s，不跳过站点3的通行时间为50 116.18 s，跳过站点降低1.6%的通行时间.类型3中，跳站后的通行总时间为56 311.76 s，不跳站时的通行时间为57 832.18 s，效率提升了2.6%.类型4中，跳站后的通行时间为58 793.63 s，不跳站的通行时间为62 021.23 s，效率提升了4.7%.从上述分析可以看出，当下车乘客的站点利用率高时，由于乘客下车必须停靠，所以此时公交车很少跳过站点.而当下车乘客站点利用率降低时，公交车跳过的站点数量随着上车乘客站点利用率的下降而增加，见表5.

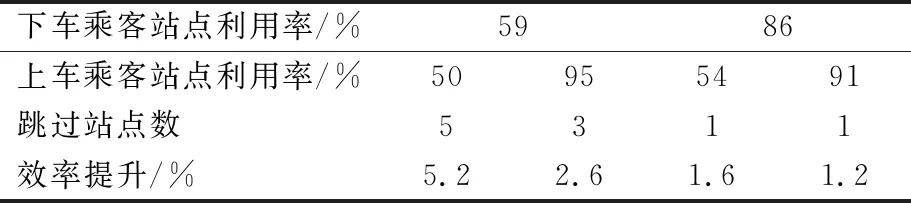
表5 乘客利用率-效率提升表

2.5.2乘客比例

乘客比例是指车辆到达某一公交站时，车上乘客数与站点等车乘客数的比值.模型中最为重要的参数就是乘客人数，公交车判断是否跳过站点要根据车上乘客数和站点等候的乘客数来做综合评判.

考虑两种情况：站点无人等车，站点有人等车.当站点无人等车时，在不考虑下车乘客的情况下，公交车可以跳过站点.当站点有人等车时，需要结合当时车上乘客数和等车乘客数来做选择.

文中主要针对站点有乘客等车的情况，分析在单个站点，公交车跳站与否与乘客数量的关系.

单个站点的通行时间Td为下式，参数同前.

Td=w·n·tdi+w·β·n·twi+

α·N·tsi+β·N·tri

(15)

通过对比站点跳站与不跳站两种情况下的通行时间，得到在当前乘客数量下公交车的跳站情况.

将不跳过该站的通行时间减去跳过该站的通行时间，得到差值：

Tp=N·tsi-w·n·twi-N·tri

(16)

当Tp>0时，表示公交车不跳过站点的通行时间更长，应该跳过该站点；同理，当Tp<0时，公交车不跳站.令Tp=0，得到

由模型可知车上乘客数和站点乘客数不是线性关系，故分别讨论站点乘客数为1，2，…人时，车上乘客数与跳站情况之间的关系.

由于乘客比例是针对单个站点的车内外乘客的比值，所以不能使用公交非直线系数的概念.在这里选择两段道路作为研究对象.

路段1见图4a)，该线路为绕行路段.路段2见图4b)，该路段为直线路段.图中罗马数字为路段编号.

图4 模拟路段

该路网中各路段的长度和平均行驶速度见表6.

首先讨论路段1.当站点乘客数为1时，用Matlab计算公交车的Tp，站点乘客1人，车上乘客数为10人时，公交车可以跳过该公交站点，跳过后，该站点可以减少3 s的通行时间.同理计算站点乘客数2，3，4的情况并汇总，见图5，其中横轴为站点等车乘客数，纵轴为车上乘客数.

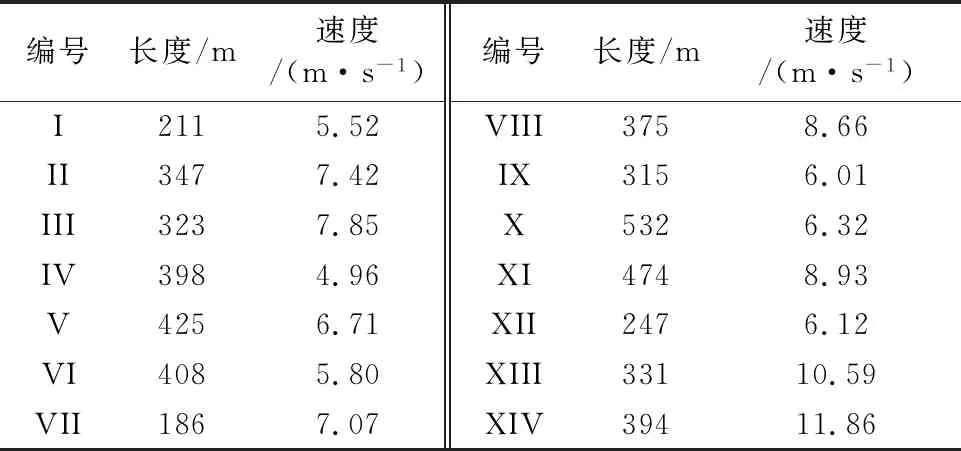
表6 路段长度速度表

图5 路段1跳站乘客数量图

讨论路段2.当站点乘客数为1时，对车上乘客数与跳站情况作讨论.用Matlab计算公交车的Tp，得到表6.站点乘客1人，车上乘客数为22人时，公交车可以跳过该公交站点，跳过后，该站点可以减少39.5 s的通行时间.同理计算站点乘客数2，3，4的情况并将线路1和线路2乘客数据汇总，见图6.

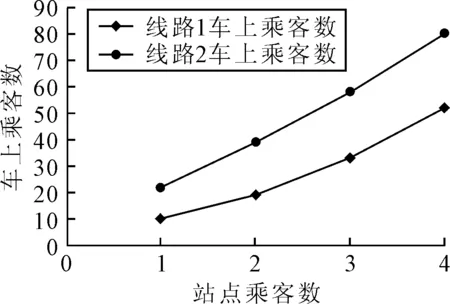
图6 路段1和路段2跳站乘客数量图

由图6可知，路段1和路段2相比，站点乘客数相同时，跳过该站线路2的车上乘客数更多，即线路2能够跳过站点所需的车上乘客数更多.

3 实例分析

选取武汉909路公交车为例，公交线全长45 km，起点站为珞喻路吴家湾，终点站为梧桐湖新区凤凰苑，沿途共50个公交站.起点站珞喻路吴家湾周边分布有武汉众多大学，距离光谷广场较近，所处地理位置较为繁华，人员流动密集，乘客人数较多.而终点站梧桐湖新区凤凰苑临近鄂州市，属于武汉周边乡镇，沿线路过众多乡镇、村落，乘客人数分布比较不均匀，在长达45 km的公交线路上，乘客上下车的站点相对集中.路线图见图7.

图7 909路公交路线图

将公交站点做编号，同时测量其站点间距，对沿线的公交乘客数做调查，得到沿线每一个公交站的乘客上下车数量(发车时间间隔定为10 min)，见图8.其中阿拉伯数字标志站点编号，英文字母表示交叉口编号.

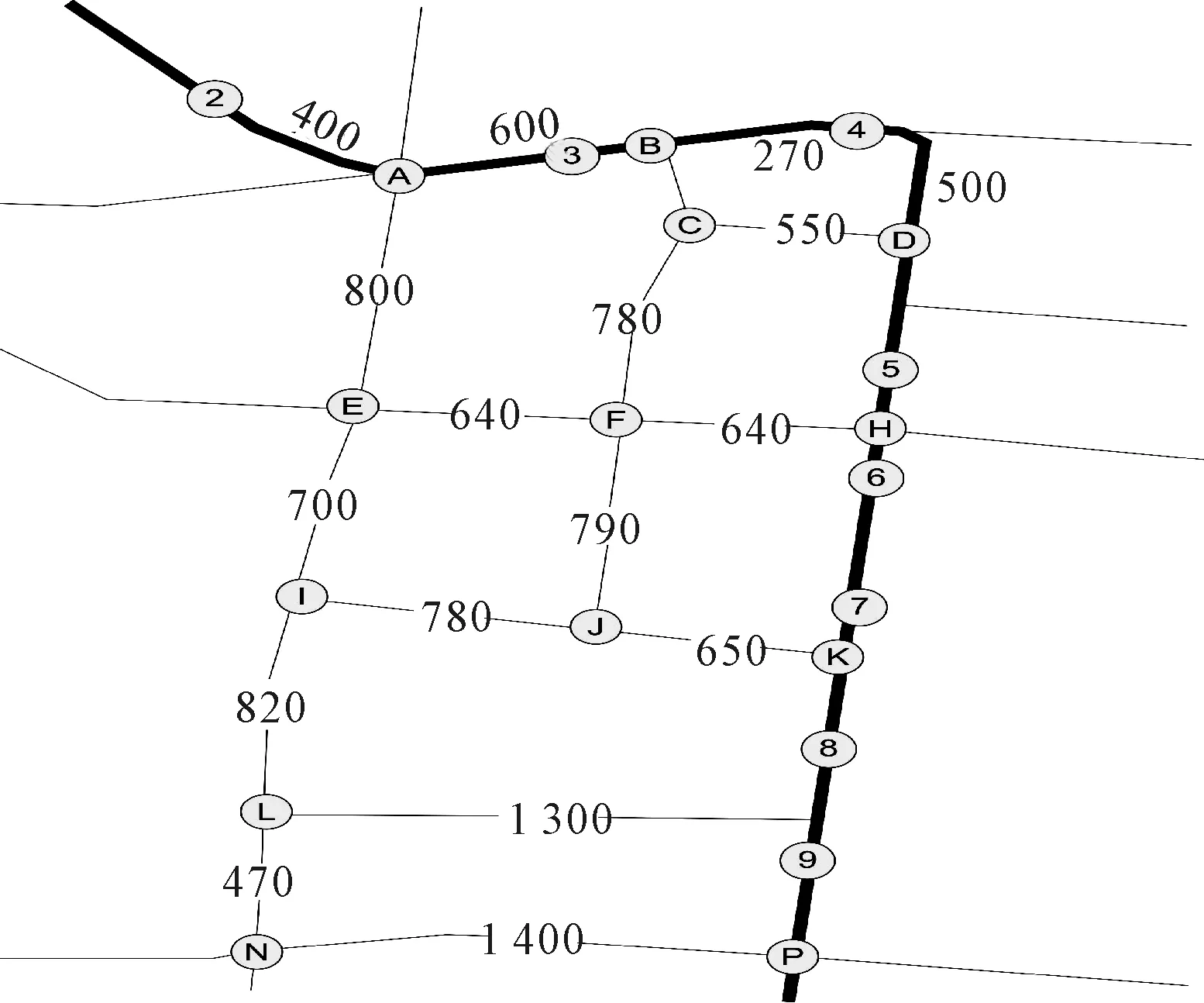
图8 原公交线路

调查公交乘客数和各个路段的长度和通行速度，见图9.运用dj算法，求解公交车到达下一站点的最优路线，最优路线的选择以行驶时间最小为目标.得到站点3～8的各个站点的最优路径，见表7.

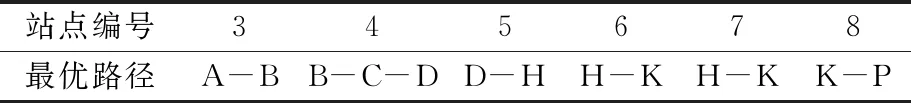
表7 各站点最优路径

通过Matlab运算，得到公交车的停靠站点为编号：1-2-7-9-10-11-13-14-16-17-18-19-20-21-22-23-25-27-29-32-34-37-38-39-40-45-48- 50的公交站.该路径跳过了21个站.其中站点3，4，5，6四个站可以被跳过，跳过后，相应的最短路径为A-B-C-D-H-K.具体路线见图9.

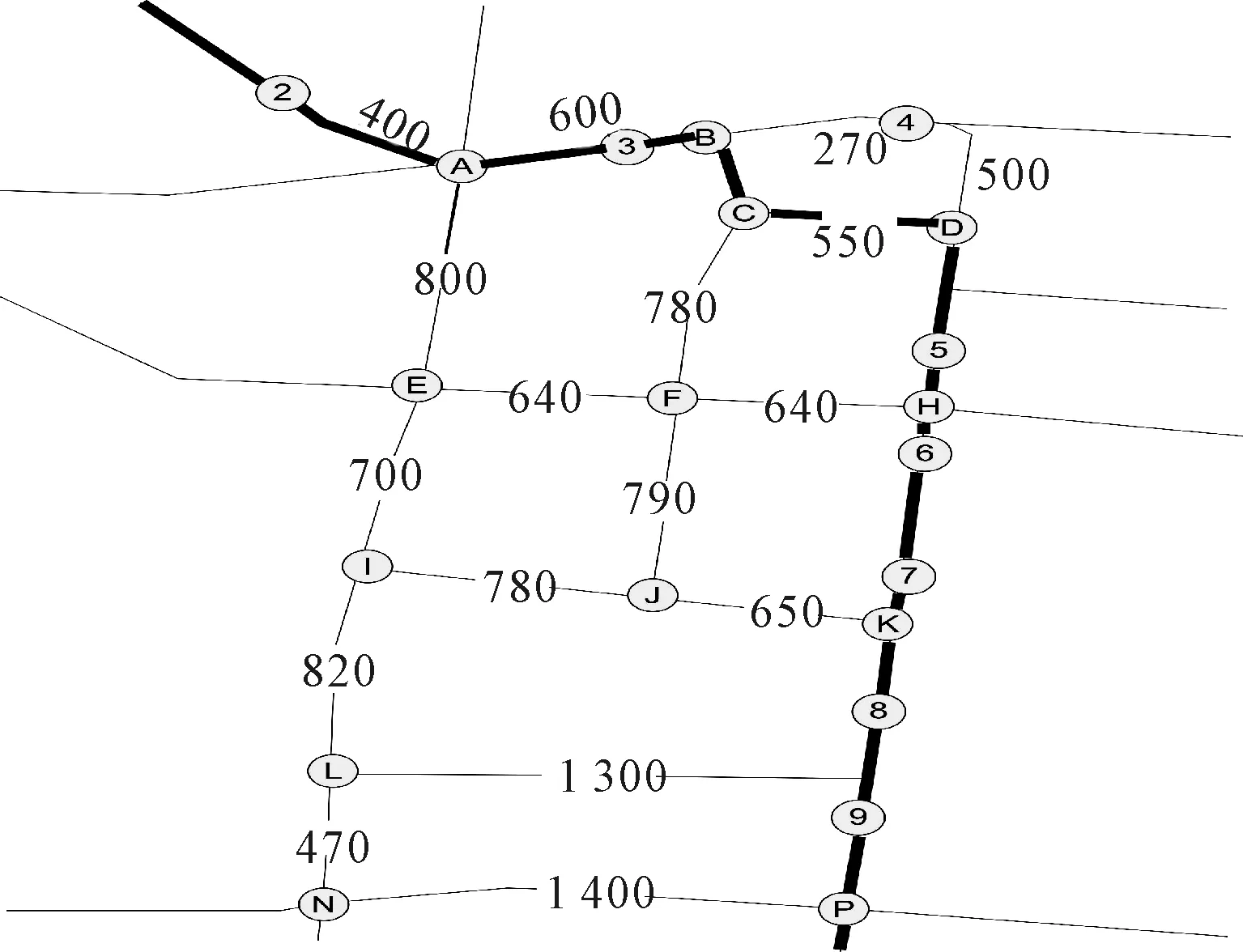
图9 新公交线路图

改变线路后，公交车载着28名乘客从站点2直接行驶至站点7，共有3人没能上车，没有乘客需要下车.改变路径后，公交车到达站点7所需要的乘客总时间为7 804.7 s，3名没能上车的乘客将继续等待，等待时间为2 951.7 s，而原线路所需要的时间为11 715.2 s，则可以得到，采用非固定公交运行模式，公交车在该段节省的乘客出行时间为958.8 s，通过该站点公交运行效率提升了8.2%.

对于整条公交线路来说，沿原线路行驶的公交车乘客出行总时间为：2 134 min；而当公交车按照跳站变线模式运行时，公交车乘客的总出行时间为2 058 min.乘客的总出行时间减少76 min，效率提升3.5%.

4 结 束 语

文中主要基于原线路站点的动态公交模式做了研究.允许公交车跳过公交站并适当改变行驶路径.在相关假设的前提下，以站点乘客总出行时间最小为目标，建立了公交跳站模型，利用dj算法寻找公交最优路径.同时，针对沿线公交站点利用率和乘客比例对模型做了参数分析，并选取武汉市909路公交线对模式做了实例验证，验证了文中模型的有效性.