互联电网联络线功率控制与全过程仿真技术*
汤 涌
(中国电力科学研究院电网安全与节能国家重点实验室 北京,100192)
引 言
我国80%以上的能源资源分布在西部和北部,70%以上的电力消费集中在东部和南部,供需相距800~3 000 km,需要远距离、大容量能源电力输送。为了满足能源电力输送需求,我国电网由省级电网和区域(东北、华北、西北、华中、华东、西南及南方)电网逐步发展形成为世界上装机容量最大、电压等级最高、电网结构最复杂的互联电网。其中,接入发电厂1万余座,建有3万余座变电站、各类输变电设备15亿台,输电线路总长100多万公里,共有9个电压等级,紧密互联成了一个特大型交直流电网。电网大规模互联,使得大范围配置能源资源的能力提升,经济效益显著。但是,由于互联电网是一个动态系统,送电、受电需保持实时动态平衡,一旦发生网内设备故障或者遭受雷击、山火、台风、冰雪、地震和地磁暴等外力冲击时,原有平衡被打破,故障冲击能量瞬间传至整个电网,系统状态会发生恶化,防御不当容易在薄弱环节突破稳定极限,导致故障范围迅速扩大,甚至发生大停电。21世纪以来,国际上先后发生了15次大停电事故。例如:2003年北美互联电网大停电,受影响人口达5 000万,纽约地区停电长达29h,直接经济损失达300亿美元。2012年互联规模较小的印度电网也发生了大停电,受影响人口超过6亿,经济损失巨大。
根据国际大电网组织相关事故统计报告,故障后的动态过程中,联络线连锁断开和受端电网电压崩溃是造成大停电的两大直接原因。因此,为了防范大停电事故发生,需解决互联电网安全防御问题,其关键技术包含:电网联络线功率波动理论与控制技术[1-8]、受端电网电压稳定理论与控制技术[9-15]以及电网全过程动态仿真方法与软件[16-33]。其中,前两项解决互联电网如何防御薄弱环节,后一项解决如何准确、快速定位互联电网的薄弱环节。
为解决我国互联电网安全防御面临的难题,笔者揭示了联络线功率波动和振荡机理,提出了电网主导失稳模式的辨识方法,研发了“毫秒级-秒级-分钟级”多时间尺度电力系统全过程动态仿真软件,建立了互联电网动态过程安全防御技术体系,提升了对关键输电断面联络线连锁开断、电压失稳的有效防御,实现数十分钟乃至数小时动态过程的准确仿真。研究成果应用于我国34个省级及区域电网的规划调度运行,大幅提升了互联电网动态过程安全防御能力。这里主要论述了联络线功率波动与振荡的原理和预测方法,以及电力系统全过程动态仿真软件的模型和算法的技术进展和应用。
1 电网联络线功率波动和振荡新原理
1.1 波动与振荡类型分类
联络线是指两个电网间功率交互传输的输电线路,由于距离长、功率波动大,容易引起连锁开断,是互联电网安全防御的薄弱环节。图1为互联电网及联络线示意图。

图1 我国互联电网及联络线示意图Fig.1 The schematic diagram of China's interconnected power grid and tie lines
联络线功率波动是互联电网运行中始终存在的自然现象。如果控制不当,功率波动幅值会超过联络线的功率极限,导致联络线开断,并引起多条联络线连锁开断,引发大停电事故。以2003年美加大停电为例,事故中俄亥俄、底特律、密歇根、安大略、纽约州、魁北克、新英格兰和PJM(Pennsylvania-New Jersey-Maryland)等8个区域电网间的数十条联络线发生连锁开断,引发了世界瞩目的大停电事故。但是,由于功率波动表现形式多样,影响因素众多,机理复杂,主要依靠故障计算结合工程经验进行联络线功率波动分析,缺乏理论支撑,效率低,误差大,建立理论体系难度很大。
联络线上的功率波动类型多样,根据表现形式和物理本质,笔者将其分为4类:对于周期性波动,分为强迫功率振荡、负阻尼功率振荡;对于无规律波动,分为随机功率波动、冲击功率波动,如图2~5所示。本节针对不同类型功率波动和振荡开展研究。
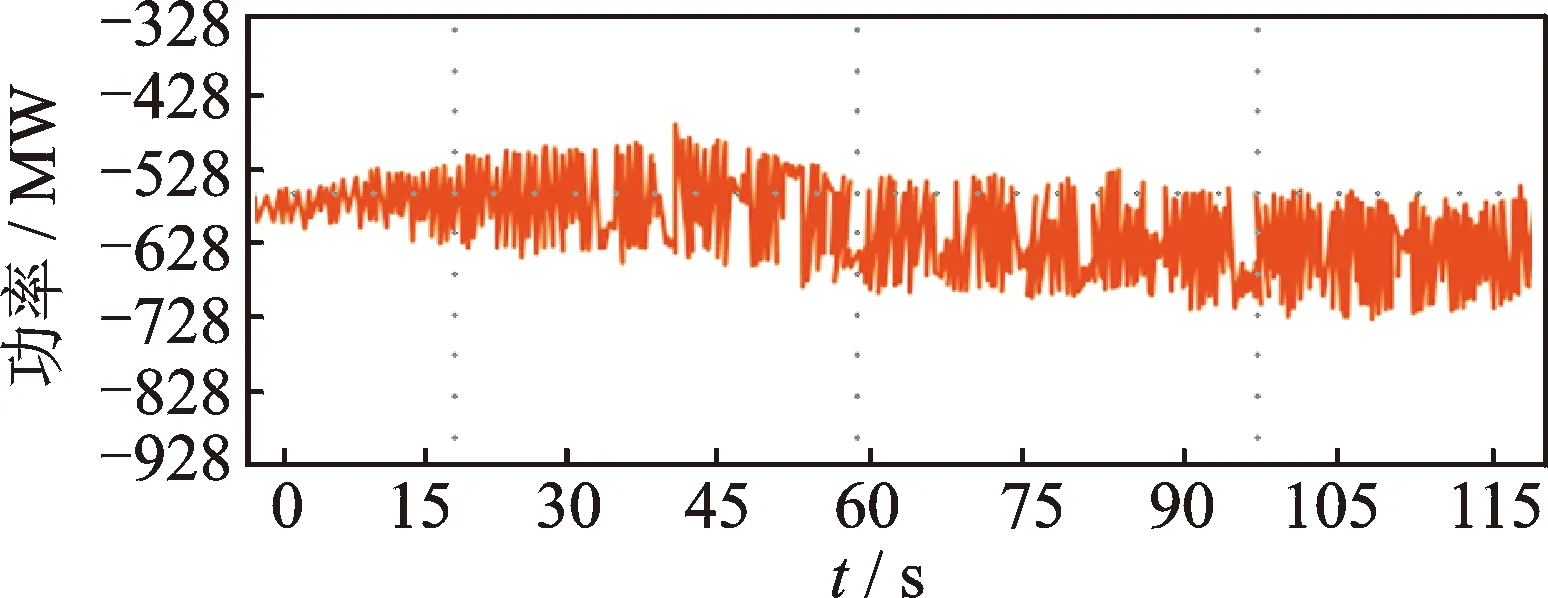
图2 强迫功率振荡Fig.2 The diagram of forced power oscillation
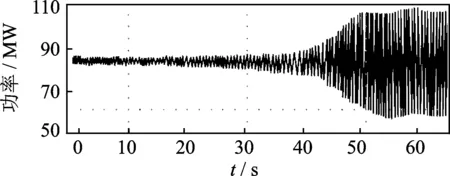
图3 负阻尼功率振荡Fig.3 the diagram of negative damped power oscillation
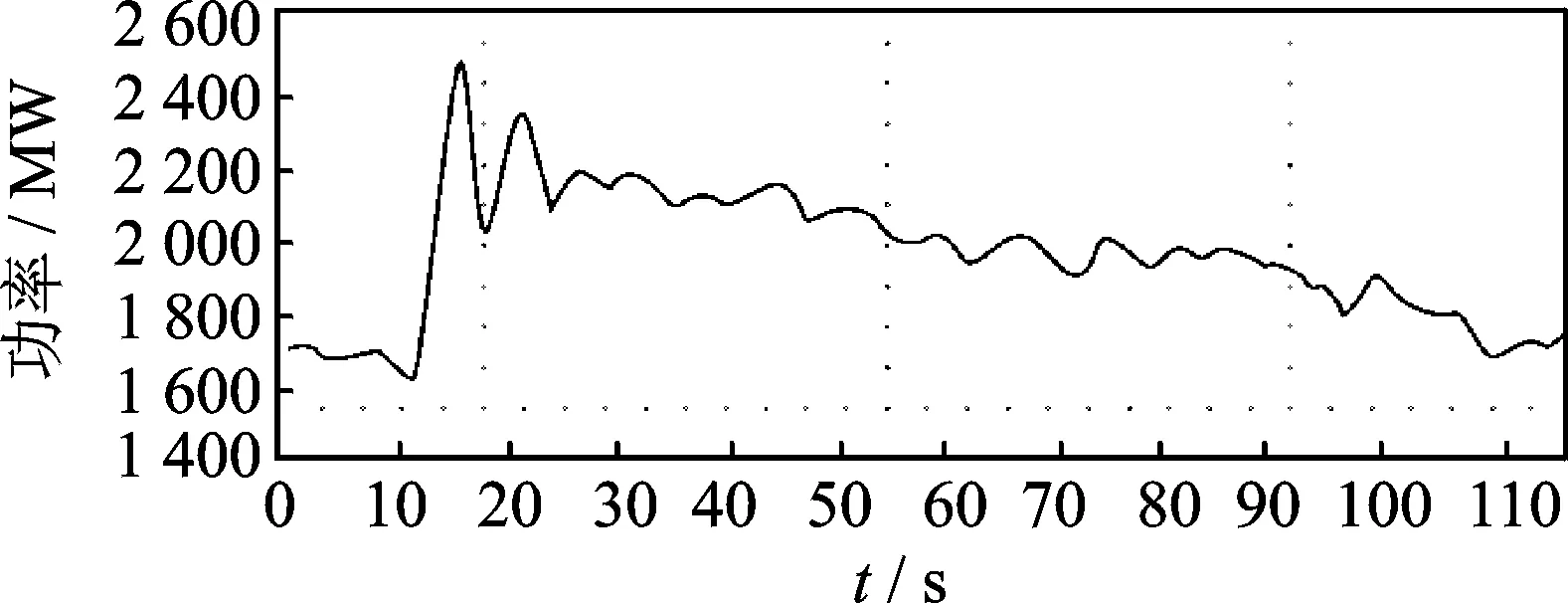
图4 冲击功率波动Fig.4 The diagram of surge power fluctuation

图5 随机功率波动Fig.5 The diagram of random power fluctuation
1.2 强迫振荡理论的新原理
我国电力系统发生了多次功率振荡现象,如南方电网分别于2005年5月13日、8月18日、9月1日发生了功率振荡,华北电网于2005年9月1日发生了蒙西电网对京津唐电网的功率振荡,华中电网于2005年10月29日发生了全网性的功率振荡,新疆南北疆于2014年12月29日发生功率振荡。这些振荡的特点是:振荡频率较低(类似于负阻尼或弱阻尼低频振荡),振荡范围广(表现为系统主振荡模式),振荡持续时间较长(几分钟到十几分钟)。振荡发生时系统均处于正常运行状态,没有明显的故障或操作,系统主振荡模式的阻尼特性较好。
上述振荡发生时,有些电网局部地区小电网存在弱阻尼,有些电网个别机组发生了负阻尼低频振荡,有些电网某些电厂运行不正常,甚至有些电网振荡时没有发现异常状况。采用常规的电力系统负阻尼低频振荡理论不能解释这些振荡现象,笔者提出的电力系统强迫功率振荡理论解释了这类非负阻尼功率振荡。该理论指出,当系统持续的周期性功率扰动的频率接近系统功率振荡的固有频率时,会引起大幅度的功率振荡,扰动所引起的响应不仅与电力系统本身的特性有关,还与扰动的变化规律有关。
电力系统的运行方程经过线性化后可表达为

(1)
上述方程的解可以写为
X(t)=UeΛtC+UeΛtV(t)
(2)
其中:X(t)为系统状态向量;C为常数向量,由状态变量初值决定;Λ为系数矩阵A的特征值组成的对角阵;V(t)为扰动函数;U为n×n阶矩阵,U的n个列向量由A的n个线性无关的特征向量组成,顺次对应的特征值就是Λ对角线上的元素。
式(2)中等号右侧第1项为系统的自由振荡,当系统的特征值λi=σi+jωi时,对应于具有一系列衰减系数为σi和振荡频率ωi的振荡。当反映系统低频振荡模式的σi>0时,则为负阻尼低频振荡。第2项为取决于扰动函数V(t)的强迫振荡。
电力系统持续的周期性小扰动可能不规则,但可用傅里叶变换将其分解为一系列周期性扰动,因此强迫振荡项可写为
d1φλ1(ωt)U1+d2φλ2(ωt)U2+…diφλi(ωt)Ui
(3)
其中
由上述分析可以看出,电力系统强迫振荡功率是由持续的周期性小扰动激起的强迫振荡,当扰动频率接近系统固有频率时就会引起系统谐振。强迫功率振荡的振幅与扰动的幅值、系统阻尼的大小有关;当持续的周期性小扰动频率接近于反映系统间振荡的较低的固有频率时,就会激起联络线较大幅值的振荡,这种振荡的表现形式类似于负阻尼低频振荡。
通过上述强迫振荡理论,能够明确系统的振荡性质,迅速搜索和定位扰动源,并采取措施快速抑制振荡。如图6所示,2014年12月29日,在新疆电网振荡事故分析中,事故当天明确了扰动性质为强迫振荡,定位了扰动源为喀发三期5号机组的调速器,找到了振荡原因并提出了解决措施。
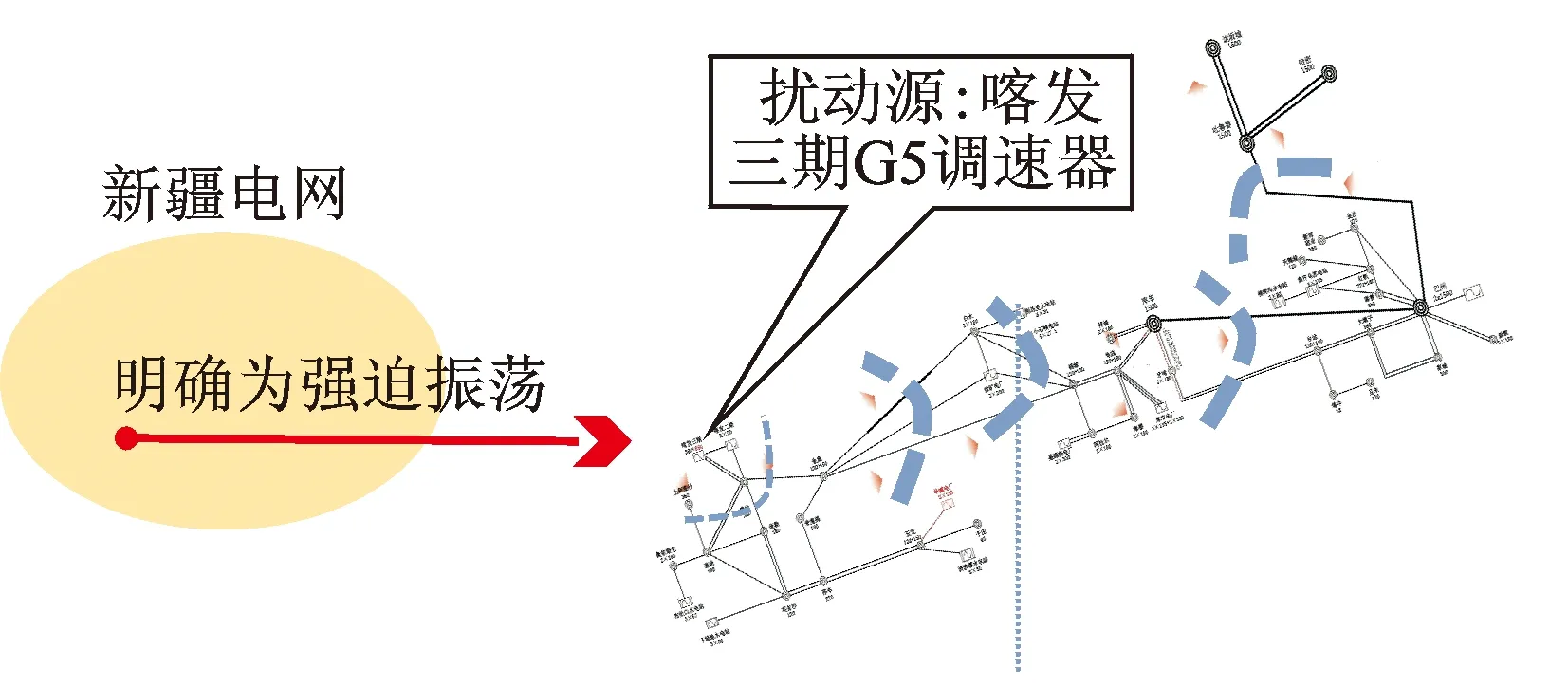
图6 新疆强迫振荡事例Fig.6 The examples of forced oscillation in Xinjiang
1.3 冲击功率波动机理及峰值预测的新原理和方法
在系统发生较大的扰动或故障后,如失去一台发电机、一个大负荷、直流闭锁、直流换相失败等产生的冲击功率,由于发电功率的重新分配,联络线将会产生大幅度的功率波动,第1摆功率波动幅值最大。此类功率波动的头摆功率峰值与冲击功率大小有关,最严重时冲击功率可能100%由联络线承担。中国长治—南阳—荆门特高压试验示范工程是目前华北和华中两大区域电网之间唯一的联络线。该工程自2008年底投入运行以来,当华中或华北电网出现功率冲击时,特高压线路上将会产生大幅度的功率波动。若扰动点在华中电网,联络线功率波动峰值常达到功率冲击的90%以上;若扰动点在华北电网,则联络线功率波动峰值为功率冲击的70%左右。随着中国更多大容量直流工程的相继投运,直流单极或双极闭锁、换相失败等故障导致的联络线功率波动幅度将越来越大,很可能造成特高压线路功率逼近甚至超过其静稳极限值,影响华北-华中互联电网的安全稳定运行。
采用传统仿真方法对故障后的联络线功率波动峰值进行计算,不但费时和模型参数精度要求高,且对机理及影响因素无法进行解释和分析。笔者提出将两大区电网等值为两机系统,进而基于2阶系统的动态响应,提出了在跳机故障、直流闭锁以及换相失败故障后的联络线功率波动峰值主导模式线性化快速预测解析算法,解决了仿真计算方法不能准确模拟故障后的联络线功率波动的问题。下式为联络线功率波动的解析表达式
(6)
其中:ΔP为系统失去发电机、大负荷、直流闭锁产生的冲击功率,当功率缺额时,ΔP为正,反之为负;ξ为互联系统区域振荡模式的阻尼比;子系统1与系统2的总惯性常数比为HΣ1/HΣ2。
(7)
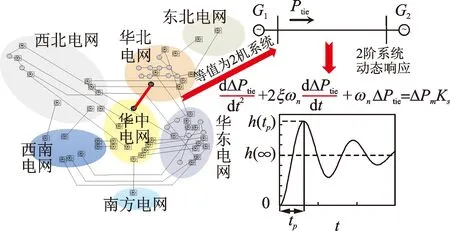
图7 冲击功率波动峰值预测思路示意图Fig.7 The schematic diagram of peak prediction of surge power fluctuation
其中:ΔPmax为直流换相失败产生的冲击功率;PDC0i为直流i的初始功率;M1和M2分别为送受端系统的总惯性常数,等于区域内各台发电机惯性常数之和;ωn为自然振荡频率;ζ为阻尼比;τ为等效换相失败持续时间。
该方法突破了由于机理不明必须穷举计算的难题,耗时由单个故障10~20 s减少到0.1 s,误差小于2.5%。
在理论研究成果的基础上,成功研发联络线功率波动联合控制系统,控制策略如图8所示。主控装置安装在四川电网,一旦感知2 000 km以外华东电网发生故障,立即判断1 000 km以外的华北-华中联络线功率波动情况,迅速决策并实施相应的控制措施,保证互联电网的安全运行。动作过程示意图如图9所示。自2001年在华北-华中互联电网中实施以来,该系统成功防御了全部大扰动冲击事件,有效保障了互联电网的安全稳定运行。

图8 联络线功率波动联合控制系统控制策略Fig.8 The control strategy of joint control system of power fluctuation of tie lines

图9 联络线功率波动联合控制系统动作示意图Fig.9 The action diagram of joint control system with power fluctuation of tie lines
1.4 随机功率波动峰值预测新原理和方法
特高压试验示范工程投入运行后,在正常运行过程中可以观察到联络线上存在随机功率波动的情况。通过分析联络线功率的相量测量单元(phase measurement unit,简称PMU)录波曲线可知,这种功率波动具有明显的无序性,波动周期一般为数十秒到数分钟,且具有随机性,波动幅值也同样具有随机性。
随机功率波动是负荷和风电、光伏发电功率的随机变化在全互联电网中再分配后在联络线上的反映,是一种稳态过程,不能用机电振荡模型描述。理论上,若能够测量并统计得到互联电网各子网的功率波动量及常规发电机功率的调整量,则可估计出系统频率和联络线功率波动的幅值。但在实际电网中,一方面由于系统中负荷站点数量巨大,在同步相量测量装置尚未覆盖到全网负荷点的情况下,要准确测得某一时间断面上系统的总负荷和总发电情况是非常困难的;另一方面,由于要求测量的各变化量(ΔPGA,ΔPGB,ΔPDA和(ΔPDB)为系统2个平衡点之间的差值,而实际电力系统总是处于动态过程中,即使在获得系统同一时间断面的总负荷和总发电曲线的情况下,也很难确定其变化量。
笔者综合考虑负荷、风电和光伏等随机功率波动源,提出了随机波动峰值概率估计方法,如图10所示。具体计算如式(8)~(10)所示
其中:ΔPABi为样本总数;Δfi为从实测的PMU曲线上得到的第i个频率波动幅值样本;KA*和KB*分别为系统A和系统B的静态频率特性系数的标幺值;CAi和CBi分别为系统A和系统B采样时刻对应的系统容量;f0为系统额定频率;E(|ΔPAB|)为联络线功率波动幅值的均值;D(|(ΔPAB|)为联络线功率波动幅值的标准差;n为样本总数。
利用该公式首次发现了联络线随机功率波动峰值、频率与输电能力之间的双指数对应规律,提出了计及随机功率波动的输电断面运行限额计算方法。

图10 联络线随机功率波动峰值预测方法Fig.10 The random power fluctuation of tie line
采用本研究方法对华中-华北特高压联络线功率波动幅值的估计值与实际统计值进行对比,如表1所示。结果表明,功率波动幅值均值的估计值与统计值的偏差小于3%,标准差的偏差小于8%,估计结果在工程允许的误差范围内。国家电力调度控制中心应用该成果确定华中-华北特高压联络线运行限额时,限额受限幅度下降33%,经济效益显著。
表1 华中-华北特高压联络线随机功率波动估算与实际对比
Tab.1 The comparison between estimation and practice of random power fluctuation of Central China-North China ultra-high voltage alternating current tie line

时间估计值实际统计值均值EP/MW标准差SP/MW均值EP/MW标准差SP/MW2011-05-2523686233932011-06-2021883224862011-07-1022783228852011-07-312248222988
2 电力系统全过程动态仿真原理与算法
2.1 电力系统仿真的作用及意义
仿真分析是掌握互联电网特性的必要手段。电网的运行是不能中断的,电网发展建设、运行控制和安全防御策略都不可能在实际电网中进行破坏性试验验证;互联电网规模巨大,设备/元件数目达数百万个以上,不能实现物理模拟,只有通过数字仿真或数模仿真,才能分析掌握互联电网的特性,验证理论分析和安全防御策略的准确性,为电网提供定量决策依据。
互联电网是一个大规模非线性动态系统,含有不同时间尺度的动态过程。直流输电、风电和光伏发电等电力电子装备的响应为毫秒级,发电机和负荷等元件的响应为秒级,整个互联电网的动态响应为分钟级。不同时间尺度动态过程相互交织,毫秒级快速暂态过程对秒级、分钟级动态过程的影响凸显,需要研发3个时间尺度统一的全过程动态仿真方法和软件。
电力系统全过程动态仿真是将电力系统毫秒级(电磁暂态)、秒级(机电暂态)和分钟级(中长期动态)过程有机地统一起来进行数字仿真,能够描述电力系统受到扰动之后整个连续的动态过程。全过程动态仿真主要涉及发电机及其励磁系统和动力系统、动态负荷、电力电子元件等动态元件和输电网络等组成的非线性动态系统。描述这一非线性动态系统的是一组高阶的微分方程组和代数方程组。仿真中模型的时间常数差异很大,混合着快速和慢速动态过程,是典型的刚性非线性动态系统。由于描述电网动态特性的微分-代数方程组(DAE)刚性比大(1∶105),对求解的数值稳定性、收敛性要求高,而电网动态过程有时可长达数小时,算法和模型微小误差的积累会导致仿真结果的极大偏差。此外,电网的微分-代数方程组阶数高(10万阶以上),对计算速度要求也很高,同时电网设备种类多,全过程动态仿真对设备模型参数的精度要求高,建模难度很大。
2.2 电磁暂态-机电暂态混合仿真算法
机电暂态-电磁暂态混合仿真算法的基本思想是根据对电力系统各区域研究重点的不同,把电力系统分解为3个部分:电磁暂态子系统、机电暂态系统以及接口母线。含有电力电子装置的详细系统定义为电磁暂态子系统,使用电磁暂态程序进行详细仿真;把传统的外部交流电力网络定义为机电暂态系统,使用机电暂态程序仿真;联接两个子系统的母线定义为混合仿真的接口母线,电磁暂态子系统和机电暂态子系统通过接口母线进行两种仿真的同步和数据交换。由于机电暂态程序基于基频、单相、相量模型,而电磁暂态基于详细的三相瞬时值模型,所以两个子系统的相互等值和接口变量选择是机电暂态-电磁暂态混合仿真算法的研究重点。
机电暂态-电磁暂态混合仿真是在机电暂态仿真中采用电磁暂态模型对高压直流输电等电力电子装备进行详细电磁暂态仿真,使用状态变量法对高压直流输电系统的换流器暂态行为进行仿真,而外部交流网络使用机电暂态稳定仿真算法。接口母线选择为换流器终端母线,如图11所示。
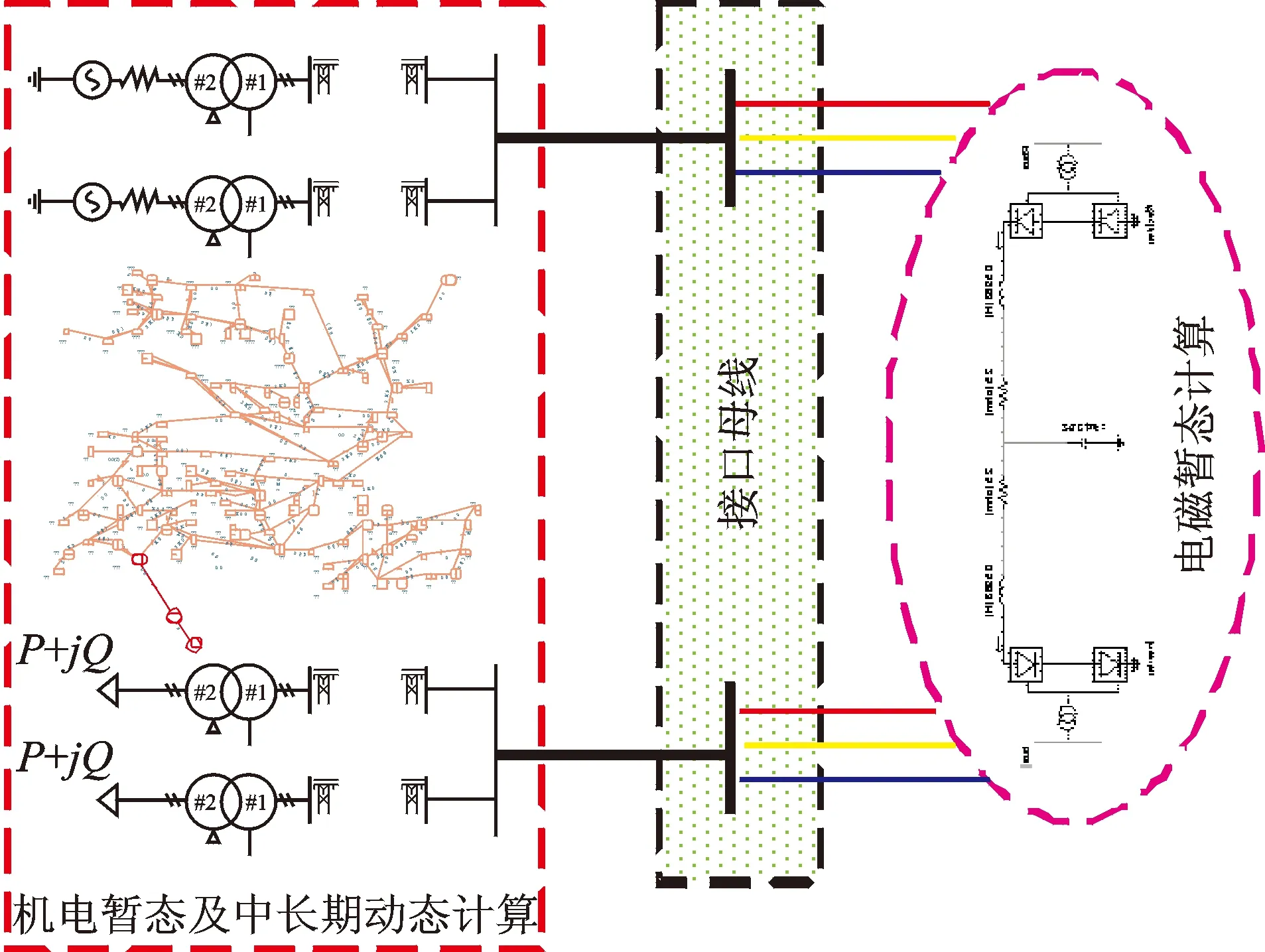
图11 电磁暂态与电磁暂态混合仿真接口示意图Fig.11 The Interface diagram of electromagnetic transient and electromagnetic transient hybrid simulation
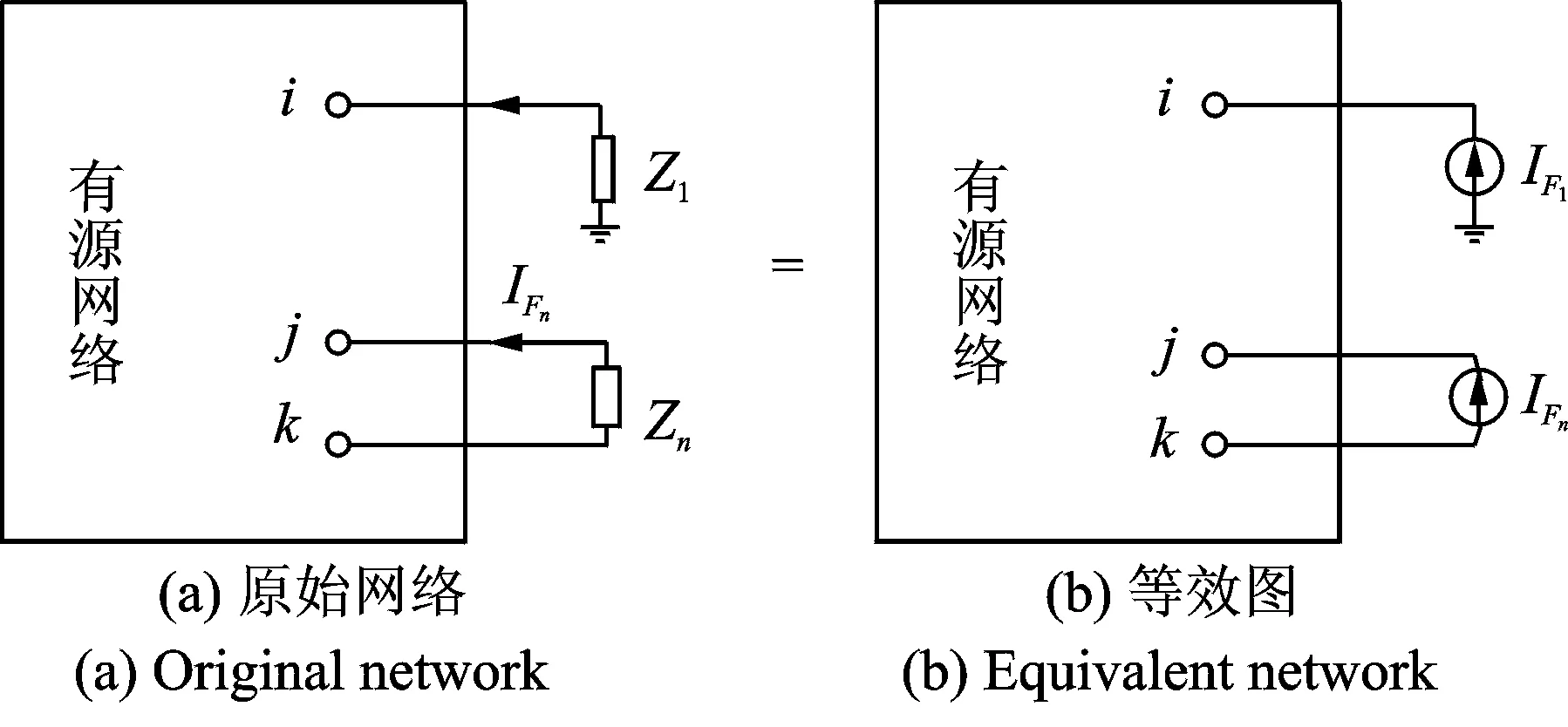
图12 补偿法的原理图Fig.12 The schematic diagram of compensation method
由于网络中含有多条高压直流或灵活交流输电元件,接口母线的数量不止一个,可以采用多端耦合诺顿等效电路(戴维南等值也是等效的)代替外部交流系统进行电磁暂态仿真。主要是利用补偿法计算直流端口的等值导纳阵和电流源。补偿算法的等效电路如图12所示。图中:Z1,Z2,…,Zn为端口连接的附加阻抗。
根据替代定理,在已知阻抗中电流的情况下,端口阻抗的变化量可以用该电流代替,即可以等效为图(b)。
电磁暂态-机电暂态混合仿真首次实现了机电/电磁暂态混合仿真,及多馈入高压直流系统的混合仿真,提高了互联电网的仿真精度。
2.3 多时间尺度数值积分算法
对于电力系统全过程动态仿真来说,电力系统全过程动态仿真中需要求解的微分-代数方程组可表示为
(11)
其中:微分方程表示电力系统元件的动态特性,为系统的状态方程;代数方程表示电力系统元件的静态特性,主要为系统的网络方程;y1为n1个状态向量(微分变量);y2为n2个代数向量(代数变量)。
全过程动态仿真对象通常是大规模交直流电力系统,其规模可达成千上万个母线和支路、数千台发电机及其控制系统、数十条直流输电线路,方程阶数常达10万阶以上。电力系统全过程动态仿真中往往有频繁的自动装置动作,产生很多的机电暂态过程,导致在较长的仿真时间内积分计算只能使用很小的步长。
全过程动态中微分代数方程组的秩为1,是一个隐式的非线性微分代数方程组,能够使用刚性微分方程理论和算法进行数值积分求解。现有数值积分方法大多采用Gear类变步长方法,例如:瑞典的SIMPOW程序、法国和比利时的EUROSTAG程序。这种方法的优点是暂态过程及中长期动态过程可以采用统一的模型和数值积分方法,在中长期动态过程中可以大步长进行仿真。在应用实践中发现该方法的主要缺点为:a. 当代数方程不收敛时,Gear算法可能失效;b. 机电暂态过程中计算步长过小,导致仿真效率很低;c. 算法难以处理模型中的间断环节。
固定步长的梯形积分法和变步长的数值积分法都具有稳定性,且都是自启动的,计算中2种方法可以相互切换。因此,为解决大规模刚性微分-代数方程组求解的数值稳定性、收敛性和快速性问题,构造新算法的基本思路是在仿真中使2种积分方法得到有机结合,扬长避短。根据电力系统动态过程的特点自动选择合适的积分方法:a.在电力系统全过程仿真的机电暂态过程中采用固定步长的梯形积分法,动态元件的微分方程和电力网络的代数方程进行简单迭代求解;b.在中长期动态过程中采用变步长的Gear法,微分方程和代数方程联立求解;c.固定步长和变步长2种方法在仿真中依据一定的策略自动切换,从而在保证数值稳定性和仿真精度的前提下,大大缩短仿真时间,提高了程序的计算效率。
积分方法切换策略是算法的关键点,其依据机电暂态过程和中长期动态过程的不同特点。根据母线电压、步长和固定步长积分法的迭代次数可以判断系统处于机电暂态还是中长期动态过程。

图13 多时间尺度统一仿真算法示意图Fig.13 The schematic diagram of unified multi-time scale simulation algorithm
多时间尺度统一仿真算法如图13所示。组合算法能有效解决现有的变步长Gear法在电力系统机电暂态阶段存在的计算速度过慢和间断环节处理复杂的问题,从而大大提高电力系统全过程动态仿真程序的仿真效率和实用性。
2.4 大型稀疏线性方程组的分块求解算法
对于大规模电力系统来说,全过程动态仿真中大型稀疏线性方程组的求解是牛顿法求解其非线性方程组的核心和难点。其难度主要表现在:a. 求解规模大,且为不对称矩阵。例如,我国目前华北-华中电力系统仿真计算,母线数目通常在15 000以上,发电机数目约为1 300余台,方程组阶数约为130 000阶;b. 求解次数多,对单次求解速度要求高。对于仿真电力系统10 min的动态过程来说,求解次数常在1万次以上。
全过程动态仿真中的稀疏矩阵结构图如图14所示。虽然属于一般结构矩阵,结构不对称,但也有其特点。总体上分为A,B,C和D四大块。A,B块对应动态元件方程,A块为对角矩阵,B块为因动态方程的输入(即网络方程的求解量电压)而引入的元素。C,D块对应于网络方程,C为因计算网络方程的注入电流而引入的元素,D由网络导纳阵组成。C和D块元素数值在不发生故障/操作时,其元素值保持不变。A块中又包含许多对角小分块,基本上是每个节点生成一个对角块,每个节点的块中又可由几个小块组成, 如由发电机子块、 励磁调节系统子块等组成。因此,该矩阵具有复杂的嵌套分块结构。

图14 稀疏矩阵的结构Fig.14 Structure of sparse matrix
方程组求解分为4个步骤进行:a.分块的符号分析算法;b.分块最小度排序算法;c.分块的上下分解(lower-upper decomposition,简称LU分解)数值分解算法;d.前代和回代求解。
根据这一新算法,开发了适于全过程动态仿真的大型线性方程组求解器(electric sparse solver,简称ESS),并与由美国Florida大学的Timothy A. Davis开发的稀疏矩阵直接求解器(Clark Kent LU,简称KLU求解器)进行了详细对比。KLU代表了目前该领域大型稀疏线性方程组求解的最高水平,Matlab也把其作为线性方程组的求解器之一。
以全过程动态仿真中2个线性方程组为例进行了上下分解、前代和回代求解时间对比。2个方程组阶数为54 603和126 869。表2为方程组求解一次耗费的计算时间对比。LU分解方面,KLU耗时为ESS求解器的2倍左右;前代和回代求解方面,ESS求解器比统一求解算法的速度略快。
表2 数值分解与求解时间对比
Tab.2 Comparison of numerical decomposition and solution time

阶数LU分解时间/ms前代回代求解时间/msESSKLUESSKLU54 6030.5141.0720.2030.233126 8691.3412.4100.5030.605
2.5 电力系统多时间尺度全过程动态仿真软件
研发出世界首套“毫秒级-秒级-分钟级”统一仿真的电力系统全过程动态仿真软件(PSD Power Tools),软件界面如图15所示。实现了数十分钟乃至数小时动态过程的准确仿真,为分析确定关键输电断面和电压失稳风险区域提供了必要手段。

图15 电力系统全过程动态仿真软件(PSD Power Tools)Fig.15 The whole-process dynamic simulation software of power system (PSD Power Tools)
全过程动态仿真软件得到广泛应用,已成为我国电力规划设计单位、调度运行部门、科研院校的基础仿真工具,市场占有率超过80%。
全过程动态仿真软件与美国PSS/E、欧洲EUROSTAG等国际先进仿真软件相比,在仿真时间尺度、算法收敛性和求解效率等方面全面超越,如表3所示。
表3 全过程动态仿真软件国内外对比表
Tab.3 The comparison of whole process dynamic simulation software at home and abroad

比较内容技术指标国际先进技术指标比较结果仿真时间尺度3种时间尺度美国PSS/E、欧洲EUROSTAG等软件具备1~2种时间尺度仿真准算法收敛性仿真不会中断欧洲EUROSTAG,SIM-POW等存在仿真中断问题适应性强 求解效率(10万阶方程组)1.86 ms美国KLU求解器:3.0 ms效率高
全过程动态仿真软件采用面向对象的思想设计了程序的架构,在灵活性、可维护性、开放性和模块化等方面较传统的仿真软件都有明显的提高。通过实际电网事故反演,验证了笔者提出的全过程动态仿真算法和模型以及仿真软件的可靠性、有效性和准确性。
3 结束语
本研究成果取得了电网安全领域的重大技术突破和突出创新,并广泛应用,具有重大的经济和社会效益,为我国电网安全稳定运行提供了技术保障,国家电网大停电事故发生率由20世纪70年代末的年均19次降到近20年的0次,电网安全达到了世界最高水平。
随着我国电网的蓬勃发展,大电网的复杂性正不断提升,尤其是近年来风电、光伏和直流输电技术的大规模运用,让电网运行控制的复杂性和难度不断增加,新一代电力系统安全运行面临更大挑战。团队将继续围绕我国能源电力发展面临的基础性、共性和前瞻性问题开展研究。
由笔者主持的国家重点研发计划项目“大型交直流混联电网运行控制和保护”,将提出安全稳定协调控制理论、故障分析方法及直流线路超高速保护方法、主动保护原理,研发大规模交直流电网全电磁暂态仿真软件,研制稳定控制样机、快速保护样机。该成果将引领大型交直流混联电网运行控制保护技术发展,有力保障大型交直流混联电网安全。
由笔者作为项目负责人的国家自然科学基金集成项目“基于数字仿真的大电网人工智能分析方法研究”将针对大电网仿真分析与决策的人工智能这一科学问题,开展大电网仿真分析知识经验的人工智能建模和应用方法、大电网仿真分析知识发现、大电网潮流方式智能分析与调整、大电网稳定性智能分析与控制4个方面的研究。构建大电网仿真人工智能分析原型系统,将先进的人工智能技术与大电网仿真分析结合,通过仿真计算产生海量样本并验证研究成果,实现对人工分析的有效替代,显著提高大电网海量潮流和暂稳数据分析的工作效率和准确性,推动电网仿真分析和人工智能技术的共同进步。未来,团队将继续支撑我国电网低碳清洁、安全高效发展和运行,持续为电网发展提供强有力的技术保障。

