基于磁偶极子模型的水下目标定位与跟踪

向 前， 马小龙

(1.武昌工学院信息工程学院，湖北 武汉 430065；2.武汉工程大学电气信息学院，湖北 武汉 430205)

0 引言

我国海洋面积辽阔，随着海上运输、口岸贸易、海上石油与天然气开采等活动的发展，重要港口与重要沿岸设施连接的水域、航道等水上活动区域以及水上设施的安全保障亟待加强。其中一项重要的威胁来自于蛙人、UUV等水下小目标。水下小目标具有隐蔽性好、突袭性强等特点，随着现代科技的迅速发展，各种水下装备不断推陈出新，如蛙人运载器、水下机器人等小型武器平台对海军舰艇基地、民用港口、海上钻井平台等海滨重要设施进行攻击，可造成巨大的生命和财产损失。针对这种情况，各国均大力研究针对蛙人、水下机器人等水下目标的探测技术。如英、美、加等国针对港口和重点目标构建了基于声纳的监视及防御系统[1-3]。但在浅海复杂环境下，声学探测易受到背景噪声、多径干扰、水中生物活动的影响，从而影响探测定位的稳定性，且声探测存在一定的暴露性。由于水下目标附属的氧气瓶、推进器等刚制装备在地球磁场中会被磁化，具有一定的磁特征，由于磁定位方法不受水文条件影响，无暴露性问题，因此采用磁方法进行近岸敏感水域水下目标的探测和定位近年来引起了广泛的重视。

根据磁传感器的类型，磁定位可分为基于矢量磁传感器的定位方法[4]和基于标量磁传感器的定位方法两大类。为了消除地磁场及其他共模干扰，基于多矢量磁传感器测量磁场梯度张量的磁定位方法是目前的研究热点[5-8]，但其需要同时工作的传感器多达6～9个，引入的测量误差较多，计算较复杂，影响了解算的稳定性。本文将水下目标磁性装备建模为一个磁偶极子，研究了基于双三轴磁传感器磁场测量数据反演磁偶极子磁矩以及空间位置，从而实现对水下目标定位和跟踪的方法。

1 磁偶极子模型

由于当传感器与目标磁体之间的距离大于目标磁体尺寸10倍以上时，该磁体可以用磁偶极子作为模型建模[9]，因此基于磁偶极子模型的探测方法在兵器引信、水下打捞、钻井对接、医疗等特殊领域均有一定应用[10-12]。

磁偶极子模型的经典数学表达式为：

(1)

式(1)中，B(μ,r)为磁感应强度，μ(H/m)为磁偶极子所在介质的磁导率，m(A·m2)为磁矩矢量，r为原点O到点P的矢径，r=|r|。

2 水下目标定位与跟踪方法

2.1 定位模型与方程组求解

水下目标与磁传感器的布置如图1所示。设目标的磁特征可等效为一个磁矩为M的磁偶极子，探测器由2个相隔一定距离的三轴磁传感器组成，并固定在预置探测点处。为了便于研究磁偶极子相对于测量磁传感器的空间位置，本节以磁传感器P1的三轴建立理想坐标系进行磁偶极子的位置解算和跟踪，并设磁传感器P2的三轴与磁传感器P1的三轴平行。设磁传感器P1坐标为(x,y,z)，则P2坐标为(x+d1,y+d2,z+d3)。

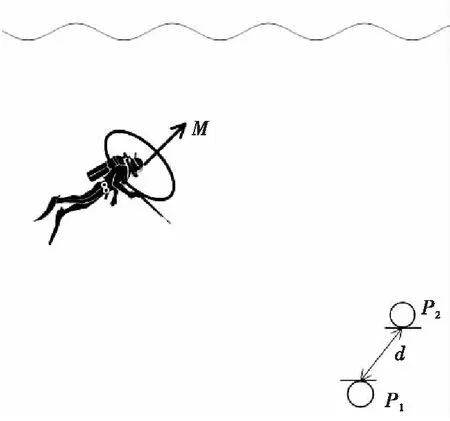
图1 水下目标磁定位传感器布置图Fig.1 Underwater target magnetic positioning sensor arrangement

将各轴上的磁偶极子参数和方向矢量(1,0,0)，(0,1,0)，(0,0,1)代入方程组(2)中，磁传感器P1处的磁场强度等于三轴方向上各磁偶极矩分量所产生的磁场强度之和，计算公式可化为式(5)。

(2)

(3)

(4)

(5)

类似可推导磁传感器P2处的磁场强度公式，在此不再赘述。式(5)为非线性方程组，其中共有6个方程，6个未知数。通常可以采用牛顿法、梯度法、共轭方向法、混沌法、BFGS法、单纯形法、Levenberg-Marquardt算法(以下简称为L.M算法)等算法求解。本文采用的是基于非线性最小二乘法的Levenberg-Marquardt算法[14]。

2.2 求解有效性判据

由于磁场强度随距离的三次方衰减， 目标与传感器之间超出一定距离后由于信号信噪比降低，参数反演会出现不稳定。针对这种情况，提出以磁偶极子三分量反演值1-范数作为求解有效性的判据。

(6)

3 模型误差分析

由于磁传感器阵列安装几何误差和磁传感器自身轴间非正交等指标非理想误差，从而导致磁场测量误差，影响水下载体定位参数的准确性。本节主要对定位与跟踪方法中的主要误差源及影响进行分析。

3.1 传感器安装中心误差

设磁传感器P1，P2坐标分别为(x1+δx1,y1+δy1,z1+δz1)，(x2+δx2,y2+δy2,z2+δz2)，其中δx，δy和δz分别表示磁传感器安装坐标偏差值，皆为小量。

3.2 传感器间敏感轴指向不一致

设传感器P1与传感器P2对敏感轴之间由于安装产生的已知夹角为(α,β,γ)，其中α为P2坐标轴绕P1X轴正向旋转角度，β为P2坐标轴绕P1Y轴正向旋转角度，γ为P2坐标轴绕P1Z轴正向旋转角度，则P2坐标系到P1坐标系的旋转矩阵R1如式(7)所示。

(7)

设由于安装校正引起的角度误差为Δα，Δβ，Δγ，均为小量，则式(7)中角度(α,β,γ) 应替换为(α+Δα,β+Δβ,γ+Δγ)。

3.3 磁传感器三轴非正交

如前所述，磁传感器P1三轴(Xp,Yp,Zp)与理想正交轴(X,Y,Z)之间存在偏差。设Zp轴与Z轴重合，坐标面YpZp与坐标面YZ共面；Yp轴与Y轴夹角为φ，Xp轴与XY面的夹角为θ，Xp轴在XY面的投影与X轴的夹角为φ。φ，θ，φ为小量，则被测磁场在理想坐标轴上的分量到传感器输出轴上实测分量之间的转换矩阵R2如式(8)所示。

(8)

上述误差因素对磁传感器输出的磁场测量数值的影响均为线性关系[15]。

4 定位算例与仿真

4.1 蛙人目标定位

以水下蛙人目标定位实验结果为例。设磁传感器P1坐标为(0,0,0)，d1=2，磁传感器P2坐标为(2,0,0)，传感器信号信噪比为20 dB，蛙人目标等效磁偶极子在三轴上分量的磁矩分别0.6，0.25，0.7(A·m2)。

蛙人在水下做水平匀速直线运动，速度为1 m/s，采样频率为2 Hz。传感器P1收到的信号经低通滤波去除地磁等静磁干扰后并归一化后如图2所示。x轴方向实际轨迹和本文方法反演得到恢复轨迹如图3所示。

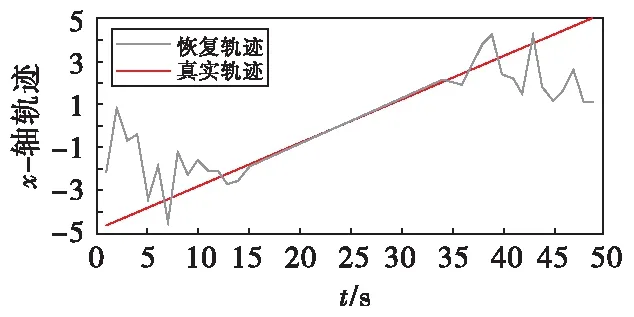
图3 x轴方向实际轨迹和采用本文方法反演得到恢复轨迹Fig.3 The actual trajectory of x-axis and the trajectory recovered by using the method in this paper

从图3和图4可以看出，反演结果在目标距传感器一定距离内，才可以稳定地反演出目标的磁偶极子分量和位置，而超出这一距离，反演结果将会发散，因此这里采用1-范数作为反演解有效性的判据。蛙人目标等效磁偶极子三轴分量范数如图4所示。

图4 磁偶极子分量1-范数Fig. 4 1 norm of magnetic dipole component

在上述实验条件下，得到有效距离内的目标定位误差为x轴3.4%，y轴7.3%，z轴0.47%。

4.2 误差分析

为进一步验证方法的定位效果，进行了误差仿真分析实验。仍取传感器P1的中心点为原点，三轴对应的理想坐标系为参考坐标系，P2坐标为(2,0,0)。设目标磁偶极子在三轴上的磁矩分量为M=[2,2,2] (A·m2)，在(5,-5,5)，(5,5,5)，(-5,-5,5)，(-5,5,5)确定的平面内按1 m间隔选取定位点，如图5所示。

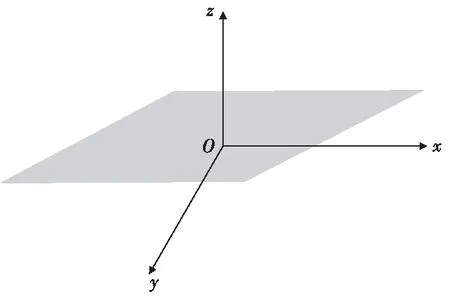
图5 算法仿真方法示意图Fig.5 Sketch map of simulation experiment

设传感器安装中心误差小于0.05 m，传感器间指向角度误差小于2°，磁传感器三轴非正交夹角小于0. 1°。传感器信号信噪比为25 dB，考虑到实际应用，定义当定位误差大于10%时，即认为定位失败。在设定区域的定位成功率仿真结果如表1所示。

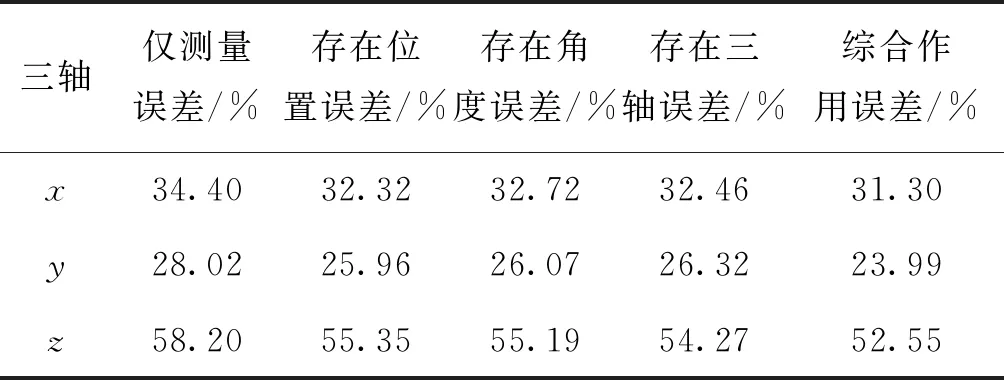
表1 目标定位成功率

从表1可以看出，本实验条件下的定位成功率主要反映了指定区域中有效定位区域的大小。本文方法在存在安装几何误差、传感器非理想指标等因素的情况下，有效定位区域有所减小，但仍具有较好的稳定性。验证了第三节关于误差影响的分析。

5 结论

本文提出了基于磁偶极子模型的水下目标被动定位方法，并分析了其主要误差及影响。该方法采用双三轴磁传感器测量数据通过对目标等效磁偶极子模型进行反演解算，实现对目标的定位与跟踪，模型简洁，计算量小。计算与仿真实验表明，本文算法可以得到水下目标的三维方位及距离信息，具有较高的精度和稳定性，可以做到实时计算。由于磁场强度信号衰减较大，对目标的探测距离较近，下一步需采用更高精度、低噪声的磁场强度传感器，提高对于水下目标的有效定位与跟踪距离。