考虑节点过载的碳排放空间关联系统级联失效模型

黄光球 谢蓉

摘 要：为提高突发事件级联失效对现实碳排放关联系统破坏程度的评估可信性，在传统复杂网络的“负载容量”级联失效模型基础上，考虑个体成员对负载的冗余能力，提出一种过载失效概率，构建了考虑节点过载状态的级联失效模型，并基于节点特性提出了6种过载节点负载分配策略。仿真结果表明：在过载节点负载分配策略中，综合分配策略整体上较优，能够有效控制级联失效的规模，增加网络鲁棒性;在一定范围内提升过载参数有助于降低级联失效的影响，但提升到一定程度时改善效果不明显;在不同负载分配策略下，剩余系数存在一个最优值，容量可调参数存在最优区间，可以使碳排放关联网络保持较好鲁棒性的同时，花费较小的构建成本，其中紧密度分配策略对应的网络构建成本较高。

关键词：碳排放关联网络;级联失效模型;过载节点;负载分配;魯棒性

中图分类号： TP393

文献标志码：A

Abstract： In order to increase the creability of the damage degree evaluation of cascading failure caused by emergency to carbon emission correlation system， considering the redundancy ability of individual members to load， an overload failure probability was proposed based on “load-capacity” cascade failure model of traditional complex network， and a cascading failure model was constructed considering load overload. Then， based on the characteristics of nodes， six load allocation strategies for overloaded nodes were raised. The simulation results show that， in the load allocation strategies of the overloaded nodes， the integrated allocation strategy is superior in general， which can effectively control the scale of cascading failure and increase the robustness of network; increasing the overloaded parameters in a certain range can help to reduce the impact of cascading failure， while the improvement effect is not significant when the parameters are too large; under different load allocation strategies， the residual coefficient has an optimal value and capacity adjustable parameters have optimal ranges which can keep the carbon emission correlation network in good robustness with low construction cost while the tight allocation strategy means high costruction cost.

Key words： carbon emission correlation network; cascading failure model; overloaded node; load distribution; robustness

0 引言

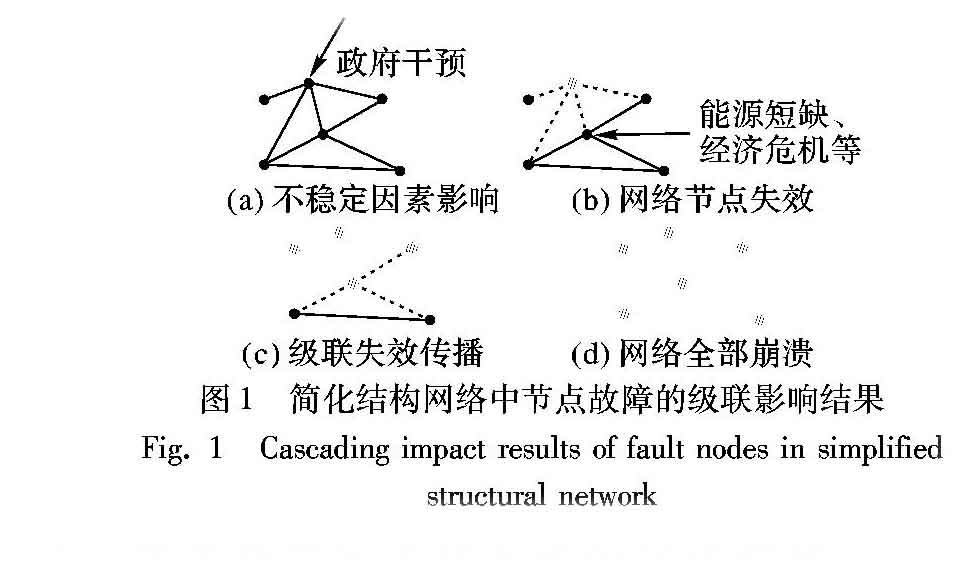
现实社会中，产生碳排放的主体彼此相互依赖，它们通过资金、技术等经济往来联系在一起，逐渐形成一个复杂化、规模化的碳排放关联系统，但系统本身常表现出不稳定的情况，如能源短缺、经济危机等;同时当主体的碳排放水平过高时，政府或企业便会响应节能减排号召采取一定措施，如搬迁出高耗能企业、改革产业结构等，以降低碳排放，此时主体成员“故障失效”，继而影响到与其他主体成员间的经济往来，特别是当系统内重要的参与主体或主要的环节“失效”时，关键链路消失，级联失效传播，严重时可导致整个网络的瘫痪，如图1所示。故不能忽视这种失效现象的存在，尤其是对一些核心主体，那么客观有效地分析和改善碳排放关联系统的级联失效就成为一个需要重点关注的问题。

在交通网络[1]、电力网络[2-3]、通信网络[4]等方面，级联失效现象早已引起学者们的关注，可是针对碳排放关联网络的相关研究较少。随着我国一系列区域碳协同减排发展战略的实施，空间依赖性增强，碳排放的关联特征逐渐成为研究热点[5-6]，但动态的级联失效过程分析涉及不多。在级联失效模型方面，Motter等[7]最早提出ML（Motter-Lai）模型，根据节点度为负载赋值、仿真，发现移除负载最大的节点足以瘫痪整个网络。Dou等 [8]提出非线性容量负载模型，针对多种网络模型，从网络费用和鲁棒性两方面进行了研究。Bao等 [9]发现不同网络在不同情况下呈现的抗毁性相反。丁琳等[10]分别以节点度、介数为依据进行加权，结果表明，参数在特定值下网络抵抗级联失效的鲁棒性最强。在失效节点的负载分配方面，Wang等[11] 、段东立等[12]分别提出了一种负载局域、全局及中间分配策略的级联失效模型，并进行了级联失效的仿真。

既有模型大多未考虑节点的过载状态，失效均为确定性的模式，且缺乏对过载节点负载分配的探讨。现实系统中的个体通常存在一定的冗余能力，具有些许弹性，并非负载超过其容量就会失效，只是负载的持续增加会使其更易失效。基于此，本文考虑了节点的过载状态，对碳排放关联系统动态级联失效问题进行研究，以过载系数描述节点对于负载的冗余能力，以失效概率刻画失效的不确定性，提出了更贴近于现实碳排放关联网络中失效情况的级联失效模型，有助于拓展级联失效研究的思路。

1 碳排放空间关联系统的网络构建

碳排放关联系统中不仅包含有多种类型生成碳排放的社会成员以及碳排放关系链，而且随着社会经济的迅速发展，成员间相互交流的方式发生了很大改变，不只限于直接的能源交流方式，还包括有资金、信息等途径，这促进了成员之间碳排放的交流，也使得它们之间呈现出日益紧密的依存依赖关系，并且这种关系会随着时间的推移而变化。这些成员的规模和产业常常不同，在网络中也拥有不同的地位和作用，系统也因此呈现出多样性。所以对于碳排放关联系统来说，把它模拟为一种复杂网络形态更为合适，而不是用简单的线性链来描述。

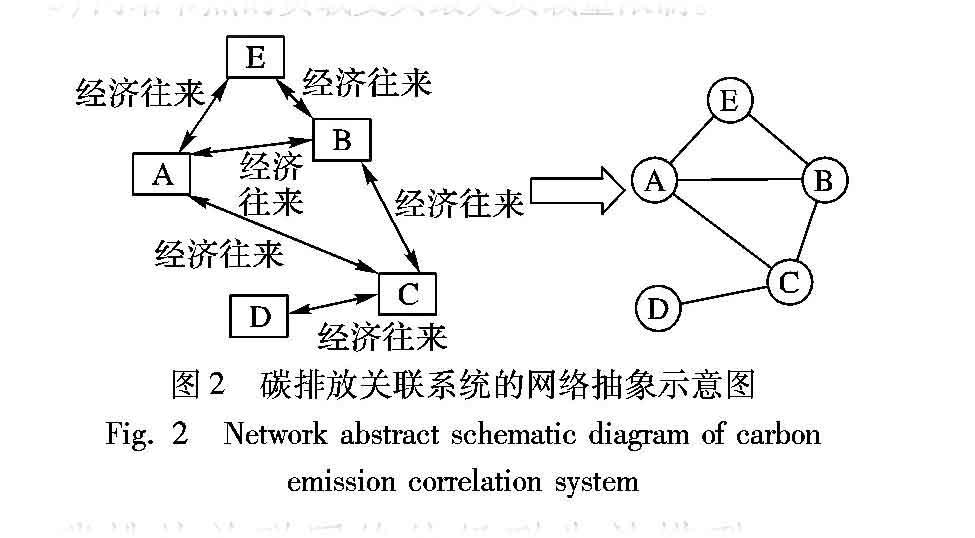
首先，认识到区域碳排放关联系统包含碳排放主体和关联关系两个基本要素。现实区域碳排放关联系统中的参与主体是有限的，本文研究主要以区域内管辖的省份、城市等为对象，它们可以用复杂网络的节点表示，任意两个碳排放主体之间有“距离”;但它们之间虽地理分离却以经济往来方式（包括资金往来、能源交流、信息交互等）联系在一起，这种相互依赖和作用的关联联系被抽象为边，网络抽象过程如图2所示，图中字母代表节点城市或省份。通过复杂网络理论和数学图论知识，可以获得碳排放关联系统的网络图集合G=（V，L），其中V={v1，v2， …，vN}是节点集合，L={（vi，vj），i，j=1，2， …，N}是边的集合。在确定了主体成员节点和边的基础上，还需引入N×N的邻接矩阵B={bij}来描述碳排放主体之间的关联关系，邻接矩阵元素的取值可以反映主体之间从事的碳排放关联活动状况，如果两主体成员vi和vj之间有关联存在，则bij=1，此时代表在碳排放关联网络中节点vi和vj之间有边相连;反之，则bij=0，此时代表节点vi和vj之间没有边相连。

关系的确定有多种方法，常用的有引力模型[6]和基于向量自回归（Vector AutoRegression， VAR）模型的格兰杰因果关系（Granger Causality）检验方法。不论选择哪种方法，本文研究都要作以下假设：

1）碳排放关联网络中主体成员之间的经济往来是双向的，认为该网络是一个无向网络。

2）研究期内，失效破坏的成员节点和边短期内不具备恢复能力。

3）网络节点的负载受其最大负载量限制。

2 碳排放关联网络的级联失效模型

如果区域碳排放关联网络中某个参与成员因外界影响而故障失效，那么它会破坏系统中信息、资金、能源等的交流往来，这将使得网络中的负载在其他成员节点或边上进行重新分配;但考虑成员的冗余能力，当节点负载大于容量限制时并非一定会失效，即为节点的过载状态，只是运行效率降低且存在一定的失效风险。基于此，改进既有的级联失效模型，考察级联传播所引起的碳排放空间关联网络的鲁棒性变化。

2.1 节点初始负载与节点容量

碳排放关联网络的组织结构是决定内部负载分布的一个关键因素，现有的相关研究[13-14]中，节点负载的估量通常引用度和介数的概念给出不同的定义。本文研究定义碳排放参与成员节点的负载出于两方面考量：一方面，现实碳排放关联关系中，成员节点更易选择距离较近的成员进行资源交互，因此认为成员节点承担的负载与该成员的局部连通效率有关;另一方面，对于现实系统中一些度较大的“富成员”，自身跟其他成员之间关联数量较多，而其他成员为了寻求信息和机会倾向于跟“富成员”建立关联关系，因此该成员承担的负载更大，这也符合城市社会系统的特点[15]。因此，定义节点vi的初始负载Fi（0）如下：

2.2 节点状态类型

在许多现实大规模碳排放关联网络中都存在一定的保护应对策略，过载的成员不一定会崩溃失效，如果负载能得到及时疏散，有可能会恢复正常。以过载参数γ来刻画节点vi对于额外负载的处理能力，γ>1，则其可承受的最大负载为γFi′，节点的过载参数越大，意味着网络鲁棒性在一定程度上就越强。当负载Fi大于等于γFi′时，节点一定失效;当负载Fi大于Fi′且小于γFi′时，节点以一定概率失效。因此t时刻节点vi的状态表达式gi（t）如下：

大多数情况下，节点对于小范围的过载較为敏感，失效的概率增长较快;超过一定范围后，失效概率增长速度减慢，这体现在式（4）中。当失效持续时间τ=T0，函数h的导数表现为先增加后减小。 当过载参数γ=γ0，函数m体现失效持续时间τ和失效概率P（τ）|γ0之间的关系，并假设P（τ）|γ0服从均匀分布。因此，当过载参数为γ0，时间T0过后，其失效概率为P0;倘若经过时间段为0.5T0，则得到该过载节点的失效概率为0.5P0。式（5）表明，失效概率函数P与过载比例γ和过载持续时间τ呈正相关关系，当过载比例和过载持续时间增加，失效概率也随之增加，这也与碳排放关联系统真实情况吻合。

2.3 节点负载分配过程

每个成员节点vi在碳排放关联系统中都承担着一定作用，当它故障失效后，模型中不得不考虑其原本承担负载的分配疏散，这里讨论多种负载分配方式。首先，将故障节点vi的负载Fi以节点度策略分配至其相邻节点，并更新相邻节点的负载。对于“过载”状态节点，用剩余系数δ来描述节点分配负载后自身承担的负载，满足0≤δ≤1，过载节点vi的剩余负载量为δFi′。当δ=0时，说明过载节点vi将当前负载全部进行分配;当δ=1时，表明过载节点vi仅分配多余负载，保证节点恰好处于正常状态。t时刻，过载节点vi分配至相邻非失效节点vk的分配量ΔFik如式（6）所示：

2.4 级联规模和网络构建成本评估

某个节点的故障失效会造成众多节点的状态改变，继而造成网络一定规模的级联过载或失效现象。为量化这个问题，也为了更好地表示过载这一状态，采用修正后的级联失效平均规模Saffect作为评估级联效应的测度，其计算式如下：

3 过载节点负载重分配策略

在级联失效过程中，失效节点负载的分配策略影响着网络的鲁棒性，同样，若没有及时地对过载节点的负载进行疏散，可能致使其失效并造成进一步级联失效现象。在以往的研究中，学者们一般假定分配原则是按照节点的负载或容量进行简单的平均分配[18-19]，但这并不符合现实关联网络负载路由规则。因此，本文研究基于网络局部和全局两个角度，分别对过载节点的负载分配规则进行以下6种讨论。

4 仿真实验与结果分析

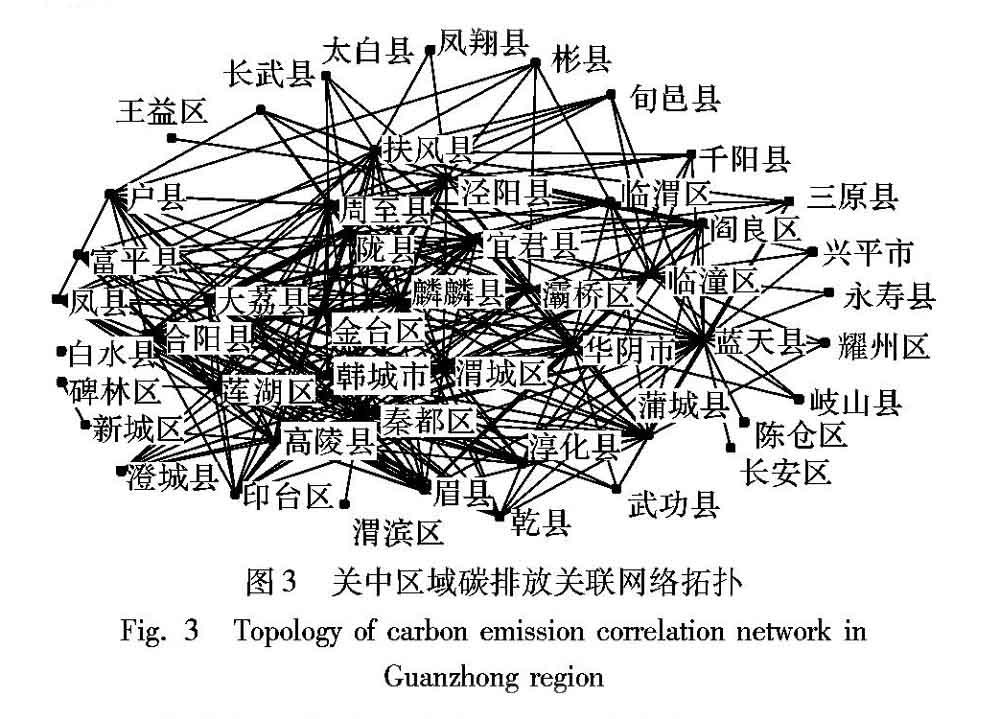
以关中区域碳排放空间关联系统为仿真对象，探索它的级联失效传播影响。在这个范围内，共有53个县（市、区）成员个体，内部在资源、技术等方面互相依赖，相互合作，形成了一个典型的区域碳排放空间关联网络。本文研究以2016年关中区域碳排放统计数据为基础进行仿真剖析，其中，社会经济数据主要来源于陕西省一系列区域性统计年鉴、政府工作报告和《陕西省统计年鉴》等。依照第1～2章提出的碳排放关联系统的网络化方法，通过引力模型获得关中区域碳排放关联网络的邻接矩阵B={bij}，如果矩阵元素bij=0，代表这两个节点之间没有连边，利用复杂网络分析法和UCINET 6.0软件，得到这个碳排放关联网络拓扑结构，如图3所示，网络结构共存在372条连边。

本文研究重点探讨级联失效过程，暂不讨论网络中初始负载分配方案，即不考虑负载可调系数α的影响，令α=1。根据成员节点的经济规模和实时处理能力，假设过载的市、区节点可以及时对负载进行疏散，不产生失效情况，即认为P<1，对于过载的县域节点，是否失效利用式（4）进行判断。采取随机攻击方式，分别从过载节点负载重分配策略、过载参数、剩余系数、容量可调节参数等方面对网络级联失效传播进行评估。

4.1 过载节点负载重分配策略对级联效应的影响

为研究过载重分配策略对级联效应的影响，将其他参数固定为β=1.2，μ=1，γ=1.5，δ=1，利用式（10）～（14）对过载节点采取不同的负载重分配策略，计算相应的Saffect值（式（7）～（8）计算得到）。在仿真结果中发现，DR、HCR、LPR策略下网络级联影响较小，因此IR策略采取以上三种策略进行加权，且权重分别取0.1、0.3、0.6时效果较好。随机选取碳排放空间关联网络节点作为初始故障节点，仿真结果如图4所示。

由图4可知，未考虑过载节点负载重分配策略时，超过容量的负载没能被及时疏散使得节点更易失效，因此网络级联失效规模最大;TR策略是所有分配策略中效果最不理想的;HCR策略、LPR策略与IR策略下网络失效规模较小，效果较好。这是由于TR策略忽略了邻居节点自身的差异，负载容量较小或是处理能力较低的节点存在着较高的失效风险;相反，HCR策略与LPR策略充分考虑了这种风险。此外，IR策略在整个过程中使碳排放关联网络保持着较低的失效规模，这是由于该策略一方面考虑了节点的度，即分散负载的路径，另一方面考虑了节点负载容量和实时处理能力，也就是可承受负载的能力，因此，IR策略相对最佳。通过仿真结果可知，对过载节点的负载进行合理疏散，可以较大程度上控制网络失效的规模，从而加强整体网络鲁棒性。

4.2 过载参数对级联效应的影响

为探讨过载参数γ对级联效应的影响，令过载节点分配策略为IR策略，并将其他参数固定为β=1.2，μ=1，δ=1，对式（3）～（5）中γ取不同的值，计算不同的Saffect值，仿真结果如图5所示。

由图5可知，当网络未考虑过载状态时，对网络级联失效规模的影响是巨大的，仅3个节点发生故障就可引起网络全部崩溃;当γ=1.5时，网络的失效规模相较于γ=1.0得到了显著控制，有7个节点故障网络才会完全崩溃;而γ=4.0时，网络崩溃则需要12个节点发生故障，表明随着参数γ的增大，网络的鲁棒性增强，级联失效的规模总体上呈现出了减少的趋势。这是因为，对于拥有较大γ参数的节点，意味着它对于额外负载的处理能力较强，它的鲁棒性有了提升，自然级联失效规模可以得到一定程度的控制，但是发现γ=3.5和γ=4.0的仿真曲线总体比较接近。

由此不难看出，过载参数γ是影响网络级联效应的一个因素，但是在节点存在小范围的过载能力时，网络失效规模可以得到显著控制，当γ增加至一定程度时，对于提升网络鲁棒性的贡献降低，因此在现实网络中，应该合理提升节点的过载能力。

4.3 剩余系数对级联效应的影响

为考察剩余系数δ对级联效应的影响，令过载节点分配策略为IR策略，并将其他参数固定为β=1.2，μ=1，γ=1.5，對式（6）中δ取不同的值，计算Saffect值，仿真结果如图6所示。

观察图6发现，当故障节点数不大于3时，对于不同的δ值，Saffect的变化相似，表明在故障节点数较少情况下剩余系数对级联效应影响不大;当δ=0.5时，网络的失效规模最大，网络鲁棒性较差;而当δ=0.8时，网络失效规模得到了最有效控制。这是由于系数δ确定着过载节点负载分配后的剩余量，当δ较小时，过载节点分配到邻居节点的负载较多，容易使邻居节点的状态转为过载或失效;而δ较大时，过载节点虽分配的负载较少，邻居节点可能维持正常，但承担部分负载自身又易过载或失效。因此，δ存在某一个值能够使节点保留一定的冗余能力来处理负载，同时又不会对邻居节点造成过多影响。

由图6可知，在IR策略下，δ=0.8即为最优的取值，同时为检验不同过载节点负载重分配策略下δ=0.8是否仍然最优，因此，对不同的δ、过载节点负载分配策略进行仿真，通过随机故障8个节点对Saffect取平均值，仿真结果如图7所示。由图7不难发现，开始时期随着系数δ的增加，不同策略下级联效应均展现出降低走向;δ=0.8时，不同过载节点负载分配策略下的Saffect在0.28到0.45之间，显然低于δ=0.1和δ=1.0时的取值，这表明，对于关中碳排放空间关联网络而言，在不同的过载节点负载重分配策略中δ=0.8时网络的鲁棒性最强。

4.4 容量可调参数对级联效应的影响

为解析节点容量对级联效应的影响，首先要分析节点负载容量模型式（2）中β、μ与Saffect的关系，令过载节点分配策略为DR策略，并将其他参数固定为γ=1.5，δ=1，故障节点数为6，仿真结果如图8所示。由图8可以看出，Saffect值随着β与μ的增大而下降，且呈现出非线性相关关系;刚开始随着β和μ的增加，Saffect值始终为1，这是由于节点容量太小以至于无法有效阻挡故障后的级联失效现象，网络一直处于崩溃状态;当β和μ增加至一定范围内时，Saffect值迅速降低，随后趋于稳定。当Saffect值发生急剧变化时所取的β和μ值是需要重点关注的，而且当节点容量增加到一定程度时，对提高碳排放关联网络鲁棒性并不明显，同时节点容量增加在现实生活中意味着发展新能源技术、增强经济交流等，网络成本随之提高，这在应用中存在一定难度，因此采用加权最小二乘法（Weighted Least Square， WLS）对该临界区域进行拟合，得到结果如图9所示，该曲线上的点即为β与μ的最佳取值点，若β和μ取值点位于曲线下方，则该碳排放关联网络无法抵抗级联失效现象。

4.5 模型优越性分析

为进一步分析改进后级联失效模型的优越性，采用文献[13]模型对真实碳排放关联网络进行节点失效后的破坏规模对比评估。两种模型的规模对比如图11所示。

根据图11发现，改进后的模型在提高网络鲁棒性方面有着明显的优越性，当故障节点数不超过2个时，网络仍可以正常运营，当故障节点数为14时，网络才会崩溃失效;而文献[13]模型对节点故障失效始终保持着较高敏感性。这是因为，改进后的模型不仅考虑了节点和网络自身的冗余能力，还考虑了过载机制下的节点失效概率问题，更好地抑制了网络级联失效破坏程度，相较文献[13]模型更适用于结构复杂的实际碳排放空间关联网络。

5 结语

本文提出了一种既考虑到节点过载状态，又适用于碳排放关联网络的级联失效模型，并以关中区域碳排放关联网络为例进行仿真分析，分别从过载节点负载重分配策略、过载参数、剩余系数、容量可调参数4个方面进行研究，得出结论如下：

1）在单一分配策略当中，LPR策略和HCR策略使得碳排放关联网络抵制级联失效的鲁棒性较强;TR策略效果不理想;而IR策略兼顾了节点分散负载和承担负载的能力，所以在网络级联传播过程中一直保持着较强的鲁棒性。

2）考虑网络节点的过载状态对提高整体网络的鲁棒性是必要的，但是在一定范围内增加过载参数γ，可以有效控制网络级联失效的传播过程，当过载参数提升到一定程度时，其贡献度降低，網络鲁棒性没有显著提升。

3）在不同过载节点负载重分配策略下，剩余系数δ存在着某一值能够使节点自身保留一定的冗余能力，同时又不会过多影响其他节点，使碳排放关联网络鲁棒性达到最强。

4）从节点容量对级联失效的影响结果来看，参数β和μ与平均失效规模Saffect呈现出非线性负相关关系，而且参数β和μ存在一个最优边界，使得β和μ在较小的情况下，仍然能让碳排放关联网络保持较好的鲁棒性，这一点在实际应用中尤为重要，即花费最小的代价取得较好的效果。若考虑到网络内过载节点分配策略和节点容量模型的差异性，DR、BR、HCR、LPR、IR五种策略可使平均容量ω值较小，网络构建成本较低。

本文研究的不足之处是对攻击模式作了简化处理，实际碳排放关联系统中故障节点的选择不一定全部是随机的，而是根据同期社会经济状况来决定的，后续工作将对此展开深入研究，为碳排放关联系统结构优化和效能评估提供更加切合实际的政策建议。

参考文献 （References）

[1] WU J J， SUN H J， GAO Z Y. Cascading failures on weighted urban traffic equilibrium networks [J]. Physica A： Statistical Mechanics and its Applications， 2007， 386（1）： 407-413.

[2] WEI D Q， LUO X S， ZHANG B. Analysis of cascading failure in complex power networks under the load local preferential redistribution rule [J]. Physica A： Statistical Mechanics and its Applications， 2012， 391（8）： 2771-2777.

[3] ROHDEN M， JUNG D， TAMRAKAR S， et al. Cascading failures in AC electricity grids [J]. Physical Review E， 2016， 94（3）： 032209.

[4] 张超，张凤鸣，王瑛，等.基于复杂网络视角的航空通信网络鲁棒性分析[J].系统工程与电子技术，2015，37（1）：180-184.（ZHANG C， ZHANG F M， WANG Y， et al. Method to analyse the robustness of aviation communication network based on complex networks [J]. Systems Engineering and Electronics， 2015， 37（1）： 180-184.）

[5] 刘华军，刘传明，陈明华.中国工业CO2排放的行业间传导网络及协同减排[J].中国人口·资源与环境，2016，26（4）：90-99.（LIU H J， LIU C M， CHEN M H. The conduction network and collaborative reduction among different industries of carbon dioxide emission in Chinas industries [J]. China Population， Resources and Environment， 2016， 26（4）： 90-99.）

[6] 孙亚男，刘华军，刘传明，等.中国省际碳排放的空间关联性及其效应研究——基于SNA的经验考察[J].上海经济研究，2016（2）：82-92.（SUN Y N， LIU H J， LIU C M， et al. Research on spatial association of provinces carbon emissions and its effects in China [J]. Shanghai Journal of Economics， 2016（2）： 82-92.）

[7] MOTTER A E， LAI Y C. Cascade-based attacks on complex networks [J]. Physical Review E： Statistical， Nonlinear， & Soft Matter Physic， 2002， 66（6 Pt 2）： 065102.

[8] DOU B L， WANG X G， ZHANG S Y. Robustness of networks against cascading failures [J]. Physica A： Statistical Mechanics and its Applications， 2010， 389（11）： 2310-2317.

[9] BAO Z J， CAO Y J， DING L J， et al. Comparison of cascading failures in small-world and scale-free networks subject to vertex and edge attacks [J]. Physica A： Statistical Mechanics and its Applications， 2009， 388（20）： 4491-4498.

[10] 丁琳，张嗣瀛.面向级联失效的复杂网络加权策略[J].控制与决策，2013，28（9）：1399-1402.（DING L， ZHANG S Y. Cascading failures-oriented weighting strategies on complex network[J].Control and Decision， 2013， 28（9）： 1399-1402.）

[11] WANG J W， RONG L L， ZHANG L， et al. Attack vulnerability of scale-free networks due to cascading failures [J]. Physica A： Statistical Mechanics and its Applications， 2008， 387（26）： 6671-6678.

[12] 段东立，吴俊，邓宏钟，等.基于可调负载重分配的复杂网络级联失效模型[J].系统工程理论与实践，2013，33（1）：203-208.（DUAN D L， WU J， DENG H Z， et al. Cascading failure model of complex networks based on tunable load redistribution [J]. System Engineering — Theory and Practice， 2013， 33（1）： 203-208.）

[13] 竇炳林，张世永.复杂网络上级联失效的负载容量模型[J].系统仿真学报，2011，23（7）：1459-1463，1468.（DOU B L， ZHANG S Y. Load-capacity model for cascading failures of complex networks [J]. Journal of System Simulation， 2011， 23（7）： 1459-1463， 1468.）

[14] 袁铭.带有层级结构的复杂网络级联失效模型[J].物理学报，2014，63（22）：220501-1-220501-8.（YUAN M. A cascading failure model of complex network with hierarchy structure [J]. Acta Physica Sinica， 2014， 63（22）： 220501-1-220501-8.）

[15] 曾宇.基于级联失效的社会经济系统脆弱性研究及其弹性优化[D]. 武汉：华中科技大学，2015：82-88.（ZENG Y. Vulnerability research of socio-economic system with cascading failures and its resilient optimization [D]. Wuhan： Huazhong University of Science and Technology， 2015： 82-88.）

[16] KIM D H， MOTTER A E. Resource allocation pattern in infrastructure networks [J]. Journal of Physics A： Mathematical and Theoretical， 2008， 41（22）： 224019-1—224019-8.

[17] 郝羽成，李成兵，魏磊.考虑节点过载的复杂网络级联失效模型[J].系统工程与电子技术，2018，40（10）：2282-2287.（HAO Y C， LI C B， WEI L. Cascading failure model of complex networks considering overloaded nodes [J]. Systems Engineering and Electronics， 2018， 40（10）： 2282-2287.）

[18] 李勇，吴俊，谭跃进.容量均匀分布的物流保障网络级联失效抗毁性[J].系统工程学报，2010，25（6）：853-860.（LI Y， WU J， TAN Y J. Invulnerability study for cascading failure of the logistics support networks of capacity evenly distributed [J]. Journal of Systems Engineering， 2010， 25（6）： 853-860.）

[19] 朱林，方胜良，王劲松，等.面向体系作战的空间通信网络级联失效模型[J].系统仿真学报，2018，30（6）：2144-2152.（ZHU L， FANG S L， WANG J S， et al. Space Communication network cascading failure model oriented system combat [J]. Journal of System Simulation， 2018， 30（6）： 2144-2152.）