基于ARMv8架构的面向机器翻译的单精度浮点通用矩阵乘法优化
龚鸣清 叶煌 张鉴 卢兴敬 陈伟

摘 要:针对使用ARM处理器的移动智能设备执行神经网络推理计算效率不高的问题,提出了一套基于ARMv8架构的单精度浮点通用矩阵乘法(SGEMM)算法优化方案。首先,确定ARMv8架构的处理器执行SGEMM算法的计算效率受限于向量化计算单元使用方案、指令流水线和缓存未命中的发生概率;其次,针对三点导致计算效率受限的原因实现向量指令内联汇编、数据重排和数据预取三条优化技术;最后,根据语音方向的神经网络中常见的三种矩阵模式设计测试实验,实验中使用RK3399硬件平台运行程序。实验结果表示:方阵模式下单核计算速度为10.23GFLOPS,达到实测浮点峰值的78.2%;在细长矩阵模式下单核计算速度为6.35GFLOPS,达到实测浮点峰值的48.1%;在连续小矩阵模式下单核计算速度为2.53GFLOPS,达到实测浮点峰值19.2%。将优化后的SGEMM算法部署到语音识别神经网络程序中,程序的实际语音识别速度取得了显著提高。
关键词:ARMv8;单指令多数据流计算;基础线性代数子程序库;高性能计算
中图分类号: TP332控制器和处理器
文献标志码:A
Abstract: Aiming at the inefficiency of neural network inferential calculation executed by mobile intelligent devices using ARM processor, a set of Single precision floating GEneral Matrix Multiply (SGEMM) algorithm optimization scheme based on ARMv8 architecture was proposed. Firstly, it was determined that the computational efficiency of the processor based on ARMv8 architecture executing SGEMM algorithm was limited by the vectorized computation unit usage scheme, the instruction pipeline, and the probability of occurrence of cache miss. Secondly, three optimization techniques: vector instruction inline assembly, data rearrangement and data prefetching were implemented for the three reasons that the computational efficiency was limited. Finally, the test experiments were designed based on three matrix patterns commonly used in the neural network of speech direction and the programs were run on the RK3399 hardware platform. The experimental results show that, the single-core computing speed is 10.23GFLOPS in square matrix mode, reaching 78.2% of the measured floating-point peak value; the single-core computing speed is 6.35GFLOPS in slender matrix mode, reaching 48.1% of the measured floating-point peak value; and the single-core computing speed is 2.53GFLOPS in continuous small matrix mode, reaching 19.2% of the measured floating-point peak value. With the optimized SGEMM algorithm deployed into the speech recognition neural network program, the actual speech recognition speed of program is significantly improved.
Key words: ARMv8; single instruction multiple data; basic linear algebra subprogram; high performance computation
0 引言
近年由Intel公司創始人摩尔提出的摩尔定律已经逐渐在以X86-64指令集为代表的复杂指令集(Complex Instruction Set Computer, CISC)型中央处理器(Central Processing Unit, CPU)上失效,而以ARM为首的精简指令集(Reduced Instruction Set Computer, RSIC)型CPU则随着智能时代的到来进入了超高速发展期。ARM公司于2014年1月正式发布了首个64位架构ARMv8-A,ARMv8-A新加入数种特性,例如:更大的寻址范围、数量更多位数更宽的通用寄存器组、并发执行浮点计算的128b NEON向量单元、复合单指令多数据流(Single Instruction Multiple Data, SIMD)计算指令。
高性能计算在桌面与服务器端CPU和其他大体积大功耗的高性能计算设备上是一个常见的研究课题,早在几十年前第一台通用计算机ENIAC诞生的时候,它承担的任务就是替美国军方高效计算弹道,从数学模型的角度来看就是对一系列复杂的线性方程组进行近似求解,而求解过程也是通过一系列复杂的线性代数计算来实现的。时至今日,虽然通用计算机和中央处理器的性能可以满足普通用户的需求,但是在执行线性代数计算的时候依然还是要依赖于对应平台的基础线性代数子程序库(Basic Linear Algebra Subprograms, BLAS),针对目标硬件优化的BLAS库允许计算设备高效率的执行线性代数计算,著名的BLAS库有:AMD的ACML[1]、IBM的ESSL[2]、NVIDIA的CUBLAS[3]、TACC的GotoBLAS[4-5]、 中国科学院计算技术研究所的OpenBLAS[6]。
本文旨在提高移动智能设备上神经网络推理计算的执行效率,推理计算的执行过程中会大量调用单精度浮点通用矩阵乘法(Single precision floating GEneral Matrix Multiply, SGEMM)算法,所以面向Cortex-A72架构进行SGEMM优化,测试平台为RK3399,实验参照对象为OpenBLAS库的0.3.4版本。因为OpenBLAS库为跨多平台的开源项目,在公司的产品和实验室研究课题中有着广泛的应用[7],选取OpenBLAS作为参考对象更具备说服力。
首先根据GotoBLAS[4]的思路,实现SGEMM的计算子任务划分;其次,使用Cortex-A72架构特性[8]实现计算核心代码,用于执行划分后的计算子任务;最后,将不同的计算核心与数据重排方案匹配不同的矩阵规模。与OpenBLAS对比的实验结果为(以下为行文方便,本文实现的SGEMM为Evalite_SGEMM,OpenBLAS实现的SGEMM为OpenBLAS_SGEMM):方阵模式下,Evalite_SGEMM相较于OpenBLAS_SGEMM性能提升了170%,达到了实测峰值的78.2%;细长矩阵模式下,Evalite_SGEMM相较于OpenBLAS_SGEMM性能提升了312%,达到了实测峰值的48.1%;连续小矩阵模式下,Evalite_SGEMM相较于OpenBLAS_SGEMM性能提升了283%,达到了实测峰值的19.2%。
1 基础介绍
1.1 Cortex-A72处理器介绍
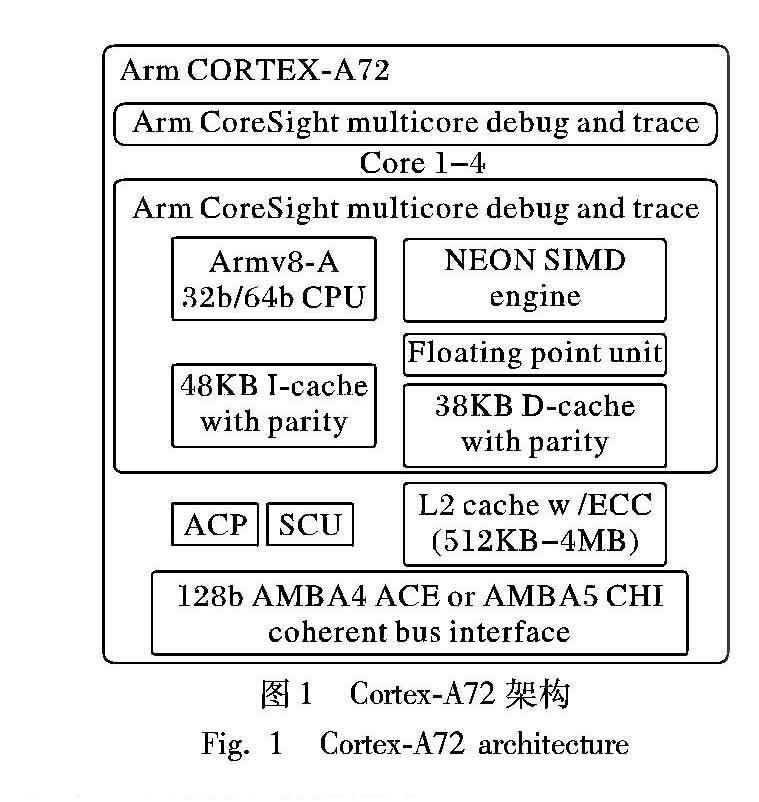
图1是ARM官方网站上展示的Cortex-A72处理器的总体架构。从图1可知,Cortex-A72同时兼容32b/64b指令集,处理器内置48KB的3路组相连L1指令cache、32KB的二路组相连L1级数据缓存(D-cache)和512KB到4MB的16路组相连L2数据共享缓存(D-share_cache),一个集成电路板上集成1到4个Cortex-A72核心,核心之间通过AMBA(Advanced Microcontroller Bus Architecture)相连。Cortex-A72处理器采用台积电16nm FinFET+制程,使得核心主频最高可达到2.5GHz。Cortex-A72采用的是3发射超标量乱序流水线,每个核心内设32个128b浮点寄存器v0~v31专门用于SIMD计算指令。
Sogou_SGEMM是移动智能设备上深度学习框架的基础数学库组成部分,以机器翻译框架为例,其中一个关键组成部分被称为转导模型[9],转导模型包含多种规格的SGEMM计算任务。针对语音方向深度学习框架中常用或者效率受限的3种矩阵规模进行调优:方阵(M=O=N)、细长阵(M=2、4,O=256,N=30000)、迷你矩阵(M≤16,O=64,N≤16)。
实现思路如下所述:第一步,实现两个高度优化的计算核心子函数SGEBP与SGEPD,旨在CPU运行这两个子函数时指令流水线更密集,同时更少地发生控制冒险、数据冒险[10];第二步,重排A、B、C三个矩阵的数据存储顺序,使得矩阵的数据存储顺序符合SGEBP和SGEPDOT在执行计算循环体时的连续读写顺序;第三步,划分A、B、C三个矩阵,使得SGEBP和SGEPD在计算一块子区域时,数据在cache与主存之间的流通次数降到最低,降低读写操作带来的额外时间开销。
2 优化实现
大规模矩阵计算的第一步是子区域分割,GotoBLAS[4]中提出的划分方案总结并分析了全部情况,所以本文的研究重心是如何利用Cortex-A72架构的特性,提升子任务计算内核代码的效率[11]。
2.1 内联汇编
参照1.1节可知,Cortex-A72的理论流水线为3发射超标量乱序,图2为Cortex-A72的流水线架构图。Cortex-A72的每1条指令在有序超标量下经过取指、译码、重命名后被乱序分派到各个执行单元上完成指令期望的操作,在不用考虑数据相关性的前提下,流水线可以在每一个cycle中同时执行3次整数计算、2次向量计算、1次分支跳转、1次读取和1次写回中的任意3条[12]。此外Cortex-A72中内置了2个SIMD计算单元NEON,NEON最初引入的目的是提高视频和音频的解码速度。发展到ARMv8架构,内置32个128b浮点寄存器,访存部件支持128b单步读写,因此本文利用NEON单元
进行SIMD计算加速。本文的实现采用的是GNU与LLVM都支持的内联汇编语法结构,在C程序中調用手动编写的汇编代码块。
内联汇编要面向的是两个不同的计算内核SGEBP和SGEPDOT,其计算模式分别如图3 (a)、(b)所示,图中M1、N1、O1、M2、N2、O2分别为各个矩阵的横纵轴,同形状点表示的是一次内联汇编循环A、B、C涉及到的数据,其中A、B的点只表示源操作数,而C的点既表示源操作数也表示目的操作数。A的行和B的列坐标分别对应的是C的行和列坐标,所以SGEBP和SGEPDOT计算模式可分别表示为式(2)~(3):
SGEBP是沿着矩阵B1的N1轴进行内循环,使得A1上的一个点跟B1上对应的一整行均相乘,相乘的结果再累加到对应的C1上一行,然后外层迭代A1沿着O1轴换到下一个点,B1沿着O1轴换到下一行,C1保持行号不变但返回到行首第一个点,当对整个O1轴都迭代1次之后,C1的一行计算就全部完成了;SGEPDOT是沿着矩阵B2的O2轴进行内循环,A2上列号与B2上行号对应的点相乘再累加到对应的C2上一点,然后外层迭代A2回到当前行行首,B2沿着N2轴切换到下一列,C2沿着N2轴切换到下一个点,当对整个N2轴都迭代一次之后,C2的一行就全部计算完成了。
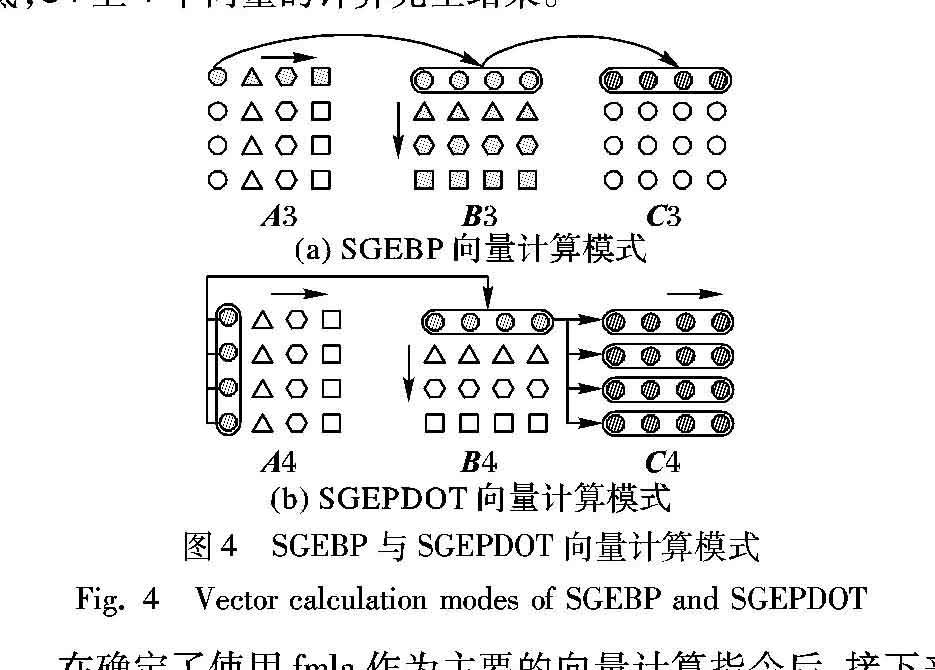
上述模式属于点对点计算,利用NEON向量化指令进行计算是优化的第一个目标,所以需要将点对点计算组合成向量计算,{fmla v0.4s,v1.4s,v2.s[0]},这条指令的功能为v2寄存器上的1个单精度浮点数分别乘上v1寄存器上的4个单精度浮点数,再累加到v0寄存器的4个单精度浮点数上,其中v0和v1的4个单精度浮点数从位高到低一一对应。fmla意味着arm可以做到1条指令进行8次浮点计算,符合矩阵乘法计算公式的基础操作,所以内联汇编将围绕着fmla展开,而使用fmla作为基本计算操作下,SGEBP和SGEPDOT的计算模式都要进行一定程度的修改, 如图4(a)、(b)所示。图中A3、B3、C3、A4、B4、C4分别是SGEBP和SGEPDOT一次内循环所需要的数据,但是利用NEON执行单元后,1条fmla指令同时计算矩阵B、C内的4个单精度浮点数。SGEBP模式A3上一个点乘以B3上一个向量再累加到C3上一个向量,直到B3一整行数据都跟A3上同一个点完成乘法计算并累加到C3一整行上,A3沿着横轴切换到下个点,B3沿着纵轴向切换到下一行,当整个B3都累加到C3同一行上,标志着C3这一行上的计算完全结束;SGEPDOT模式变为A4上纵轴4个点为1个向量取出,B4上横轴4个点为1个向量取出,然后展开4次fmla计算,并依次再累加到C4的4个向量上,然后A4沿着横轴切换到下一个向量上,B4沿着纵轴切换到下一个向量,循环计算,当A4沿着横轴循环到底,B4沿着纵轴循环到底,C4上4个向量的计算完全结束。
在确定了使用fmla作为主要的向量计算指令后,接下来研究的就是fmla在什么状态下才可以让流水线满排。这里本文参考了arm公司的《Cortex-A72优化指南》,指南里对Cortex-A72的各种指令的执行参数进行了一一列举,从指南里可以得知fmla指令在128b格式下单条的执行延迟为7个cycle,Cortex-A72有2个SIMD执行部件,并行执行延迟为3个cycle,理想的吞吐量为每个cycle完成1条fmla指令。且文档里特别说明了,混合计算指令(乘加、乘减等)实际执行的时候是将混合指令拆分成乘法、加法两条来执行,所以混合计算指令的理论峰值吞吐量为每个cycle执行1条。
为了验证文档里数据的正确性,以及验证NEON执行指令时数据相关性,参考《Cortex-A72优化指南》设计峰值测试实验,结果为峰值下每1.167个cycle完成1条fmla,循环展开3条以上目的寄存器不同的fmla下就可达到浮点峰值,与指南中给出的每cycle完成1条的结果存在16%的偏差,但测试结果显示NEON的单精度向量计算指令的数据相关性带来的延迟为4cycle,与指南中给出的数据一致。对于实测峰值为13.2GFLOPS,而理论峰值为14.4GFLOPS的状况,在与测评平台的系统设计工程师沟通分析后认为,这是由于底层的功耗調度驱动对处理器的性能进行了限制,所以测试程序实际上是在功耗受限的处理器上运行。
至此结合每个浮点寄存器可保存4个单精度浮点数的条件,想要汇编代码块在执行的时候SIMD单元利用率高,需要保证循环展开4条以上的目标寄存器不同的fmla指令,即安排4个以上的浮点寄存器用于对矩阵C的访存操作,但此点不适用于连续小矩阵乘模式的部分情况,因为小矩阵模式下C本身规模太小用不满4个浮点寄存器。
2.2 数据重排
2.1节是从计算指令的角度讨论如何让流水线满排,而没有考虑访存指令在计算中的影响,事实上计算访存比在BLAS优化中同样是一个需要的问题[13],因为当计算指令在流水线上达到足够的密度后,访存指令获取数据的效率受到缓存未命中(cache miss)情况的限制,从而限制了计算指令的执行效率[14]。本文的内联汇编计算核心在迭代执行规模为4096×4096×4096的矩阵乘法时,浮点效率3.2GFLOPS,为理论峰值的22.2%。这是因为在迭代SGEBP或者SGEPDOT的时候需要循环多次读取整个矩阵B,而本文测试使用的CPU L2 D-cache总量为512KB,当B的规模增大到512KB以上时,每次循环读取矩阵B的时候有一部分数据并不在D-cache上,需要去主存上读取,这部分数据的读取每一次都会产生cache miss,从而造成了计算效率严重下降,这是需要进行数据重排和预取的第一个原因。
第二个原因依然是从访存指令出发,从高级语言的角度来看对于数据的操作是直接的,一套复合运算用C语言书写一行计算表达式就可以描述;但是从汇编的角度来看,计算指令在执行之前需要把将要使用的变量读到通用寄存器上,主存和cache上的数据必须经过寄存器才能被CPU的执行单元进行操作,而由于数据相关性,在数据没有被读入寄存器之前,计算指令就不会执行,刚才说到的cache miss是阻碍数据读入寄存器的一个因素,而还有一个因素是执行load或者store指令时地址的变化。例如,在SGEPDOT里,load矩阵B的数据是如下格式{ldr v0,[base];add base,base,x0;},之所以要这么做,是因为B的数据是跳行读取的,x0是B的行字节宽度,在读取一行上的某个向量之后,就需要手动计算地址来定位到下一行,这也是因为虽然ARMv8支持寄存器间址寻址,但并不支持寄存器间址寻址后自动更新源地址,而相反的,如果是使用立即数间址寻址,是支持在寻址之后自动更新源地址的,也就是说如下两个格式{ldr v0,[base,#imme]!},{ldr v0,[base,#imme];add base,base,#imme}完成的是一样的功能,在使用的执行单元数量和种类相同的情况下,前一种格式只需要1条指令,而后一种格式需要2条指令,且这2条指令之间存在数据相关,即需要插入NOP来填塞流水线。
第三个原因从计算访存比出发,内联汇编代码core为了代码的简洁性和泛化性,内部实现一层循环,例如SGEPDOT的一次需要沿着0轴循环256步,不可能把256步的每一步都写成代码,正确的做法是直接写出8步或者16步的计算代码,然后循环执行32次或者16次。这就导致了一个问题,流水线想要循环执行的过程中迅速进入满排,那么计算访存比就必须足够高,根据式(1)可知,最理想的情况为在循环体内2次load就可以展开4次fmla。
综合以上3点,本文采取了以下重排方案来分别处理矩阵A与B、C。
图5(a)是矩阵A、C的重排方案,(b)是矩阵B的重排方案,同形状的点表示重拍前后同列和同行上的4个数据单元。对于A来说是将同列上4个数变为同行上地址连续的4个数,也可以看作是局部上的矩阵转置,但是无论是行还是列都必须以4的倍数进行迭代的重排,实际情况下往往行列都存在余数,那剩下的一部分并不进行重排,因为考虑剩余部分的兼容性会导致程序的结构变得复杂,且实际测试结果表明余数部分的重排并不会带来性能上的明显提升。而将A进行图5(a)所示的重排后,一次load就可以load原序里4个同列的点,由矩阵乘法计算模型可知,这4个点对应的B的数据也是相同的,换句话说就是对A进行一次load,再对比B进行一次load,就已经可以展开4次目标寄存器不同的fmla计算。对于B的重排则是进一步地强化局部的计算访存比,从图5(b)可以看出对B的重排,是以1个向量为基本单位,将同列的4个向量变为同行上地址连续的4个向量,这样2次load(ARMv8指令集支持连续地址连读、连写2个数据单元)就可以load 4个B上的向量,并与A的4个点(也可以看作为1个向量)展开16次fmla计算,且面对的是4个不同的目的寄存器,从而16次fmla可以充分利用2个SIMD单元。在SGEBP模式下,重排后的计算访存比为2;在SGEPDOT模式下,重排后的计算访存比为4;且两种模式下访存指令都可以在一定程度上被fmla指令覆盖。
此外,重排可以沿着纵轴进行延长或者缩短的。在方阵上A、B的重排可以沿着纵轴到底部的,而在2×256×30000的规模上,A只有2列,进行的就是2×4规模的重排,同时细长矩阵模式下B的全列重排占据了一次完整计算98%的时间,为了减少B全列重排对计算效率的严重影响,对于细长矩阵模式的重排本文也作了一些变化。首先,B的重排是以4行为一个子区域进行的;其次,B的重排结果在重排完成后进行暂时性的保存,也就是说当前计算完成之后,B重排后的并不只是用于最近的几次计算,而是框架模型没有进行改动之前一直重复使用,这里利用了神经网络推理计算中参数矩阵为常数矩阵的特性,每次计算时都可能发生变动的是矩阵A与C,所以对B进行一次重排之后,可以满足一整次框架运行的计算需求,甚至可以将常参数矩阵就按照重排之后的格式进行长期存储。同时对于方阵,本文作了一个细节上的优化,由于A和C都要乘以标量系数,所以在进行全局矩阵标量点乘时,本身就是对A和C的一次遍历,将这次遍历融合到A和C重排上,在矩阵小于512KB的情况下有11.2%的加速效果。
2.3 数据预取
重排完成之后,内联汇编的计算顺序和矩阵的数据排列顺序达成一致,数据在cache上得到充分重用,但数据重排和子区域划分考虑到的cache是L2 D-cache,对于L2数据cache来说能在计算中稳定保存的子区域,在32KB 大小的L1 D-cache上并不可行。ARMv8提供了数据预取指令来进一步解决高密度计算场景下的L1 D-cache miss问题,例如{prfm L1keep,[addr]}就是将接下来需要使用到的首地址为addr的数据预取到L1 D-cache中,keep的意思是指预取的这部分数据将要接下来的时间内进行多次使用,L1 D-cache就不会轻易地将这部分预取的数据刷出,还有另外一种后缀为strm,strm的意思指的是预取的这部分数据在接下来的一段时间内只计算一次,这类的预取数据在计算结束之后就会被L1 D-cache优先丢弃[15]。
使用数据预取指令需要注意3个问题:第一,预取指令的执行时间通常会超过执行访存指令并且没有发生cache miss情况下的時间,这是因为预取的数据一般是分布在L2、L3 D-cache、或者主存上,在预取数据的时候,至少发生1次cache miss,最多发生3次,所以使用预取指令的时候,要确保有足够的计算指令掩盖预取访存延迟。第二,预取指令跟访存指令使用相同的访存执行单元,预取访存延迟为几十个机器周期到上百个机器周期不等,为了保证当前计算指令依赖的数据能够提前准备好,预取指令在指令流水线上要跟正常访存指令保持一定间隔。第三,预取指令并不是将紧接的几次计算指令所需要的数据预取到L1 D-cache中,这是因为ARM的D-cache在设计上就考虑了空间局部性,假设当前计算所使用到的数据其地址为base,那么从base到 base+x地址范围内的连续数据都已经在L1 D-cache中了(其中x是根据当前计算状态在一定范围内动态变化的值),所以正在计算中使用到的数据地址为base,预取的数据地址为base+y,当y≤x时,预取就起不到任何加速作用,根据目前平台的实际测试,预取达到最好的加速效果,是预取base+320地址所指向的数据。
3 测试结果与分析
本文测试使用的硬件平台为Rockchip公司生产的RK3399芯片,内置2个Cortex-A72核心与4个Cortex-A53核心,在测试过程中只开启一个Cortex-A72核心,并锁定运行频率为1.8GHz,可计算得理论浮点峰值为14.4GFLOPS,由图6的代码实测峰值为13.2GFLOPS,考虑到芯片工艺、测试平台系统等非相关性干扰因素,本文以实测峰值13.2GFLOPS为对比基准。图6展示了3项优化工作累加之后与原始算法的计算性能对比结果。
从图6可知,3项优化工作中:对性能提升效果最大的数据重排,以4096×4096×4096规模为例,只累加向量化的版本浮点性能为3.27GFLOPS,累加向量化、数据重排实现的版本浮点性能为9.69GFLOPS,性能提升196%;其次是向量化,以4096×4096×4096规模为例,原始算法的浮点性能为2.19GFLOPS,只累加向量化的版本浮点性能为3.27GFLOPS,性能提升49%;最后是数据预取,以1024×1024×1024规模为例,累加向量化、数据重排的版本浮点性能为7.20GFLOPS,向量化、数据重排、数据预取实现全部累加的最终版本浮点性能为9.97GFLOPS,性能提升38%;最后,以4096×4096×4096规模为例,原始算法的浮点性能为2.19GFLOPS,最终版本的浮点性能为10.23GFLOPS,性能提升367%。
4 结语
本文面向ARMv8架构提出了三种不同角度的SGEMM算法优化方案,降低了移动智能设备上语音识别和机器翻译框架推理计算的时间消耗。实验结果表明,优化后的SGEMM算法在保证了计算精度前提下有效地提升了计算速度。未来的工作,还将考虑多线程优化,从而进一步提高对整个处理器的利用率,更好地降低语音识别和机器翻译框架推理计算的时间消耗。
参考文献 (References)
[1] AMD. AMD Core Math Library (ACML) [EB/OL]. [2018-09-12]. http://developer. amd. com/acml. jsp.
[2] FILIPPONE S. The IBM parallel engineering and scientific subroutine library [C]// Proceedings of the 1995 International Workshop on Applied Parallel Computing, LNCS 1041. Berlin: Springer, 1995: 199-206.
[3] QUINTANA-ORTI E S, IGUAL F D, CASTILLO M, et al. Evaluation and tuning of the level 3 CUBLAS for graphics processors [C]// Proceedings of the 2008 IEEE International Symposium on Parallel and Distributed Processing Symposium. Piscataway, NJ: IEEE, 2008: 1-8.
[4] GOTO K, van der GEIJN R A. Anatomy of high-performance matrix multiplication [J]. ACM Transactions on Mathematical Software, 2008, 34(3): Article No. 12.
[5] 蔣孟奇,张云泉,宋刚,等.GOTOBLAS一般矩阵乘法高效实现机制的研究[J].计算机工程,2008,34(7):84-86,103.(JIANG M Q, ZHANG Y Q, SONG G, et al. Research on high performance implementation mechanism of GOTOBLAS general matrix-matrix multiplication [J]. Computer Engineering, 2008, 34(7): 84-86, 103.)
[6] 张先轶,王茜,张云泉.OpenBLAS:龙芯3A CPU的高性能BLAS库[J].软件学报,2011,22(增刊2):208-216.(ZHANG X Y, WANG Q, ZHANG Y Q. OpenBLAS: a high performance BLAS library on Loongson 3A CPU [J]. Journal of Software, 2011, 22(Suppl. 2): 208-216.)
[7] CHEN B, WANG L, WU Q, et al. Cross hardware-software boundary exploration for scalable and optimized deep learning platform design [J]. IEEE Embedded Systems Letters, 2018, 10(4): 107-110.
[8] LIN I, JEFF B, RICKARD I. ARM platform for performance and power efficiency — hardware and software perspectives [C]// Proceedings of the 2016 International Symposium on VLSI Design, Automation and Test. Piscataway, NJ: IIEEE, 2016: 1-5.
[9] VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need [C]// Proceedings of the 31st Conference on Neural Information Processing Systems. North Miami Beach, FL: Curran Associates Inc., 2017: 5998-6008.
[10] WANG F, JIANG H, ZUO K, et al. Design and implementation of a highly efficient DGEMM for 64-bit ARMv8 multi-core processors [C]// Proceedings of the 44th International Conference on Parallel Processing. Piscataway, NJ: IEEE, 2015: 200-209.
[11] RUSITORU R. ARMv8 micro-architectural design space exploration for high performance computing using fractional factorial [C]// Proceedings of the 6th International Workshop on Performance Modeling, Benchmarking, and Simulation of High Performance Computing Systems. New York: ACM, 2015: Article No. 8.
[12] FLUR S, GRAY K E, PULTE C, et al. Modelling the ARMv8 architecture, operationally: concurrency and ISA [C]// Proceedings of the 43rd Annual ACM SIGPLAN Symposium on Principles of Programming Languages. New York: ACM, 2016: 608-621.
[13] LIU Z, JARVINEN K, LIU W, et al. Multiprecision multiplication on ARMv8 [C]// Proceedings of the IEEE 24th Symposium on Computer Arithmetic. Piscataway, NJ: IEEE, 2017: 10-17.
[14] XU X, CLARKE C T, JONES S R. High performance code compression architecture for the embedded ARM/ThUMB processor [C]// Proceedings of the 1st Conference on Computing Frontiers. New York: ACM, 2004: 451-456.
[15] 姜浩,杜琦,郭敏,等.面向ARMv8 64位多核處理器的QGEMM设计与实现[J].计算机学报,2017,40(9):2018-2029.(JIANG H, DU Q, GUO M, et al. Design and implementation of QGEMM on ARMv8 64-bit multi-core processor [J]. Chinese Journal of Computers, 2017, 40(9): 2018-2029.)
This work is partially supported by the National Key R&D Program of China (2016YFB0201100, 2017YFB0202803), the National Natural Science Foundation of China (11871454, 91630204, 61531166003), the Strategic Priority Research Program of Chinese Academy of Sciences (B) (XDB22020102), the e-Science Foundation of Chinese Academy of Sciences (XXH13506-204).
GONG Mingqing, born in 1994, M. S. candidate. His research interests include high performance computation, machine learning.
YE Huang, born in 1979, Ph. D., associate research fellow. His research interests include high performance computation.
ZHANG Jian, born in 1972, Ph. D., research fellow. His research interests include high performance computation, scientific computation, visualization in scientific computing.
LU Xingjing, born in 1983, Ph. D. His research interests include high performance computation, deep learning, parallel programming, compiling technology.
CHEN Wei, born in 1984, Ph. D. His research interests include human-computer interaction, machine translation, deep learning.

