基于去噪自编码器的极限学习机

来杰 王晓丹 李睿 赵振冲

摘 要：针对极限学习机算法（ELM）参数随机赋值降低算法鲁棒性及性能受噪声影响显著的问题，将去噪自编码器（DAE）与ELM算法相结合，提出了基于去噪自编码器的极限学习机算法（DAE-ELM）。首先，通過去噪自编码器产生ELM的输入数据、输入权值与隐含层参数;然后，以ELM求得隐含层输出权值，完成对分类器的训练。该算法一方面继承了DAE的优点，自动提取的特征更具代表性与鲁棒性，对于噪声有较强的抑制作用;另一方面克服了ELM参数赋值的随机性，增强了算法鲁棒性。实验结果表明，在不含噪声影响下DAE-ELM相较于ELM、PCA-ELM、SAA-2算法，其分类错误率在MNIST数据集中至少下降了5.6%，在Fashion MNIST数据集中至少下降了3.0%，在Rectangles数据集中至少下降了2.0%，在Convex数据集中至少下降了12.7%。

关键词：

极限学习机;深度学习;去噪自编码器;特征提取;特征降维;鲁棒性

中图分类号： TP181;TP391

文献标志码：A

Abstract： In order to solve the problem that parameter random assignment reduces the robustness of the algorithm and the performance is significantly affected by noise of Extreme Learning Machine （ELM）， combining Denoising AutoEncoder （DAE） with ELM algorithm， a DAE based ELM （DAE-ELM） algorithm was proposed. Firstly， a denoising autoencoder was used to generate the input data， input weight and hidden layer parameters of ELM. Then， the hidden layer output was obtained through ELM to complete the training of classifier. On the one hand， the advantages of DAE were inherited by the algorithm， which means the features extracted automatically were more representative and robust and were impervious to noise. On the other hand， the randomness of parameter assignment of ELM was overcome and the robustness of the algorithm was improved. The experimental results show that， compared to ELM， Principal Component Analysis ELM （PCA-ELM）， SAA-2， the classification error rate of DAE-ELM at least decreases 5.6% on MNIST， 3.0% on Fashion MINIST， 2.0% on Rectangles and 12.7% on Convex.

Key words： Extreme Learning Machine （ELM）; deep leaning; Denoising AutoEncoder （DAE）; feature extraction; feature reduction; robustness

0 引言

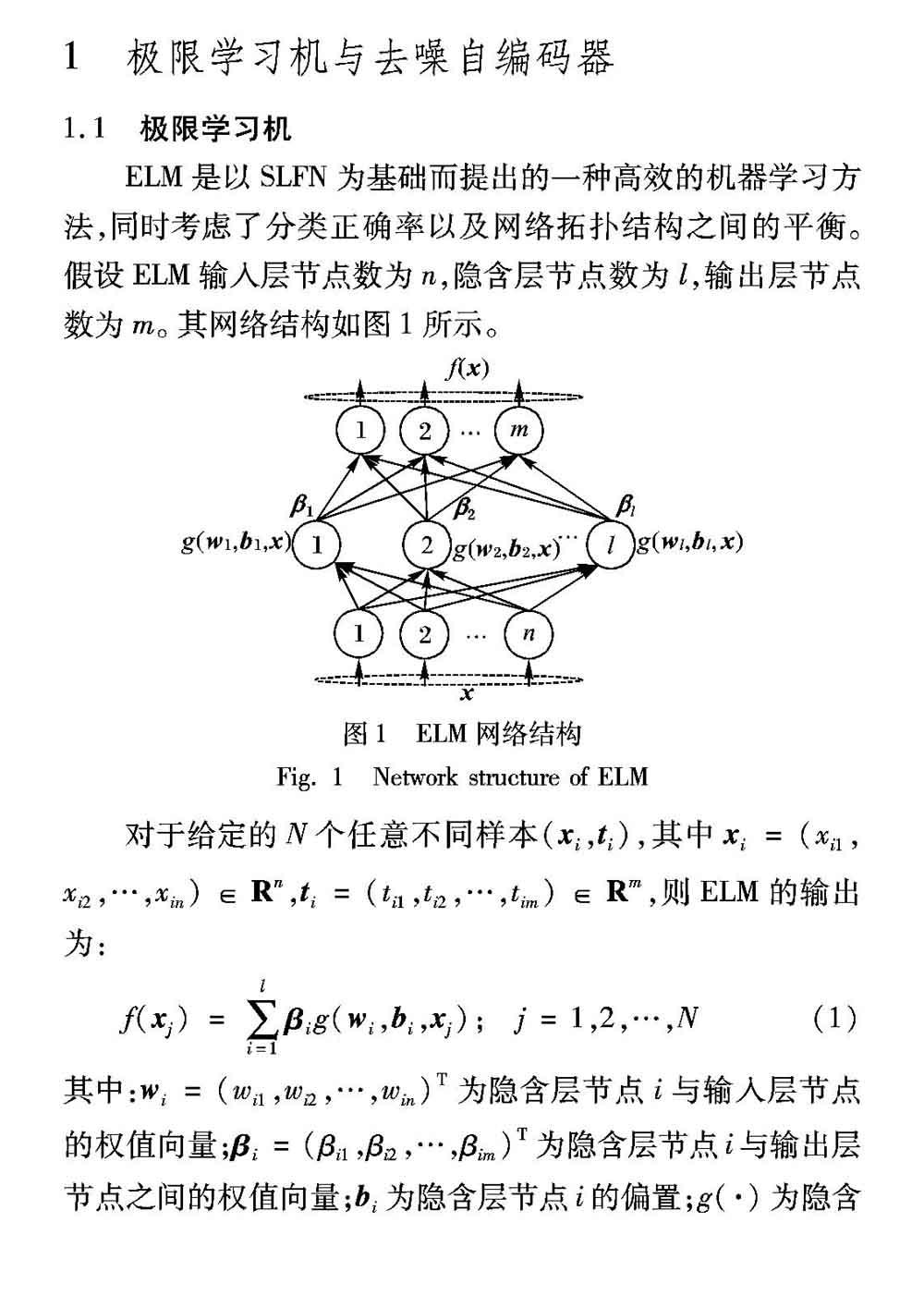
作为单隐含层前馈神经网络（Single Hidden Layer Feedforward Neural Network， SLFN）的最新研究成果，极限学习机（Extreme Learning Machine， ELM）[1]自被提出以来，凭借泛化性能优、训练时间短等特点，引起了研究者们的密切关注。同一般SLFN方法相比较，ELM的隐含层参数均为随机产生，无需进行反复的迭代，而且其输出权值为求解最小二次方程所得的全局最优解，避免了陷入局部最优解的困境。Huang等[2]证明了ELM的一致逼近性和ELM可直接应用于回归与多分类问题[3]。同时，为处理非平衡数据的学习问题，Zong等[4]通过引入类别权值，提出了加权极限学习机（Weighted ELM， W-ELM）。Liang等[5]提出的在线贯序极限学习机（Online Sequential ELM， OS-ELM），延伸ELM至在线学习问题，拓宽了其实际应用领域。目前，ELM在语音识别[6]、图像评价[7]、电力系统[8]等部分模式识别应用领域已得到初步应用。

但是当参数完全随机选择时，为保证ELM的分类性能需要大量的隐含层节点[1]。对此，学者们提出可以利用构造或剪枝的方式对隐含层节点进行参数优化，以提高ELM整体性能[9-10]。Horata等[9]通过将满足最小LOO（Leave-One-Out）误差准则的节点加入隐含层，实现对隐含层的参数优化，提出了增长型鲁棒极限学习机（Robust Incremental ELM， RI-ELM）。Rong等[10]提出的快速剪枝极限学习机（Pruned ELM， P-ELM），利用统计学原理，裁剪对分类性能影响较小的隐含层节点，以实现算法优化。但在实际应用中，此类方法对识别正确率的提升有限，这是因为基于构造或剪枝的优化方法其基本思想仍局限于传统ELM框架。当数据维数大或存在噪声干扰时，采用单一隐含层进行特征映射的方式并不适用于处理所有样本。所以，如何提升ELM算法对高维含噪声样本的识别性能是当前亟待解决的重点问题。

近年来，深度学习在高维数据特征提取方面的突出表现，使得许多的学者尝试将ELM与深度学习结合起来，以提升ELM算法性能。Chamara等[11]将极限学习机与自编码器（AutoEncoder， AE）结合起来，提出的极限学习机自编码器（ELM-AutoEncoder， ELM-AE）拥有良好的特征表达能力。基于ELM-AE，Tang等[12]提出了分层极限学习机（Hierarchical ELM， H-ELM）算法，以逐层编码实现特征的高阶表示，相较于其他多层感知器，其训练更快速、准确率更高。同时，其他的深度极限学习机算法[13-14]也为提高ELM处理高维数据的能力做出了贡献。

去噪自编码器（Denoising AutoEncoder， DAE）[15]较其他自编码器，提取的抽象特征更具代表性与鲁棒性，拥有较强的抗噪能力。受深度极限学习机算法启发，本文将DAE与ELM相结合，提出基于去噪自编码器的极限学习机（DAE based ELM， DAE-ELM）算法，用堆叠DAE先产生ELM的输入数据，然后产生输入层权值及隐含层参数，克服了传统ELM参数赋值的随机性，增强了其鲁棒性及抗噪能力。实验结果表明，对于典型高維数据集，无论是否存在噪声影响，DAE-ELM比传统ELM算法和AE算法的分类性能有明显的提升。

1.2 去噪自编码器

DAE是对自编码器的改进，其最大特点是在进行特征提取之前，加入了对原始样本数据的退化过程[17]，其结构如图2所示。

在DAE中，退化过程是指对于每一个样本，按照一定比例将其属性值置为0或其他值，这个比例被称作退化率。退化过程如图3所示（对于灰度图像，置0意味着置黑）。

DAE加入退化过程的自然原理是人眼在看物体时，如果物体某一小部分被遮住了，人依然能将其识别出来[15]。该现象说明人所带有的“生物”自编码器所提取的特征更具有代表性与鲁棒性，对于输入的含有一定噪声的样本数据，它经过编码、解码后仍能得到纯净无噪的样本。这要求自编码器不仅有编码功能，还要有去噪作用。然而，即使数据中含有的噪声，AE却只能重构含有噪声的输入数据。所以，对原始样本进行适当的退化处理，再让自编码器重构原始样本，如此提取的特征更本质、更抗干扰[15]。

DAE的学习过程包括退化、编码和解码三个阶段。首先，对输入数据按比例随机置0进行退化，得到退化数据。然后，对退化数据完成编码得到编码层。最后，解码编码层，得到输入数据的重构，通过调整各层参数使重构误差函数达到最小值，以获得输入特征的最优抽象表示。

2 基于去噪自编码器的极限学习机

ELM性能受样本数据维数、噪声影响大，且其鲁棒性因参数随机赋值而降低。而DAE所提取的特征更本质、噪声敏感性更低，所以结合DAE与ELM，由DAE获得ELM的输入样本、输入权值与隐含层参数，一方面可以提高分类器处理高维含噪声数据的能力，另外一方面可以提高分类器的鲁棒性。

DAE-ELM的网络结构及如图4所示。

DAE-ELM的学习过程如下：

1）训练第一去噪自编码器网络，提取出原始输入数据的去噪抽象特征，以作为ELM的输入数据。该网络结构如图4中DAE1所示，根据1.2节中所述，令DAE的输出数据与输入数据相同，通过反向传播算法进行训练。当重构误差函数最小时，得到最优网络参数：输入层权值w1，隐含层偏置b1及隐含层输出h1。h1为输入特征的高级抽象表示，这些抽象特征剔除了输入数据中的冗余信息，而且过滤了其中部分噪声，且当输入数据维度较高时，可以起到降低数据维度的作用。将h1作为ELM的输入数据，有利于提升ELM性能。

2）训练第二去噪自编码器网络，生成ELM输入权值和隐含层参数。该网络结构如图4中的DAE2所示，与第一去噪自编码器训练相似，只是将DAE的输出数据与输入数据均置为第一去噪自编码器的隐含层输出h1。训练完毕后，得到第二去噪自编码器的最优网络参数：输入层权值w2，隐含层偏置b2及隐含层输出h2。将其作为ELM的网络参数，可以避免输入层权值与隐含层参数随机赋值所造成的性能和鲁棒性下降问题。

3）训练ELM作为整个网络的辨别模型。ELM结构如图5中的ELM模块所示，其输入数据为第一去噪自编码器的隐含层输出矩阵h1，即原始输入数据的去噪抽象特征表示，其输入层权值与隐含层输出为第二去噪自编码器的输入层权值w2与隐含层输出h2，然后根据1.1节中所述理论训练ELM，即求解ELM隐含层输出权值β，从而完成整个网络的训练。

3 实验结果及分析

3.1 实验环境

实验平台为Intel i7-7700K 4.2GHz，16GB内存和1TB硬盘的PC，实验在Windows 7系统上用Matlab 2017（b）实现。

3.2 实验数据

DAE-ELM算法旨在提升ELM在高维含声噪数据下的泛化性能，在本文中采用MNIST[18]、Fashion MNIST[19]、Rectangles[20]和Convex[21]等数据集作为实验数据，并分别加入10%高斯白噪声与10%椒盐噪声到各数据集生成含噪声的新数据集，其详细信息如表1所示。

3.3 结果分析

为测试所提出模型的性能，设计了以下实验（需要强调的是，本文中所有实验结果皆为重复实验10次后的均值）。

实验1 网络结构确定以及与其他ELM算法在无噪声MNIST数据集下的性能对比分析。

实验2 退化率对模型性能的影响分析。

实验3 与其他算法在有噪声和无噪声环境下的性能对比分析。

3.3.1 网络结构确定与性能对比分析

对于神经网络结构，即隐含层层数、节点数的确定在目前为止暂无明确的理论指导，学者们普遍采用试错法，按照一定准则改变网络结构进行重复实验，然后采用性能最优的网络结构。因为本文需进行性能对比实验，隐层节点数目的不同将对模型性能对比的客观性产生影响，所以各模型网络隐层节点数应尽可能相同。

因为DAE-ELM含有两层隐含层，难以同时确实两层节点数，又因为第二隐含层实为ELM的隐含层，所以本文首先根据原始ELM算法隐含层节点个数对分类性能的影响以确定DAE-ELM第二隐含层节点数，然后再根据DAE-ELM第一隐含层节点数对分类性能的影响情况，确定其节点数。最后在进行对比实验时，观察隐含层节点数对各模型分类性能的影响，以判别各模型性能。

首先，使用MNIST数据集中的训练样本训练ELM模型，并使用测试集进行测试，观察分类性能随隐含层节点数的变化趋势，其中节点个数取值范围为{100，200，…，2000}。性能趋势图如图6所示。

根据图6不难发现，随着隐含层节点数的增加，ELM的训练与测试分类错误率都在逐步下降，且下降趋势逐渐放缓，符合ELM的一致逼近性。但是在保证一定分类正确率的前提下，理应考虑网络的紧凑性，减少时间与空间复杂度。在图6中，当节点数等于1500时，分类错误率较低，网络较紧凑，而且错误率下降趋势已较为缓慢，所以假定隐含层节点数为1500，即DAE-ELM第二隐含层节点数为1500。

假定DAE-ELM第二隐含层节点个数为1500后，根据重复实验的方法确定其第一隐含层节点个数。DAE-ELM的基本参数设定如表2所示，分类性能随第一隐含层节点数变化情况如图7所示。

由图7可以发现，随着第一隐含层节点数的递增，DAE-ELM的分类错误率先上升后下降，而后再上升。这表明当第二隐含层节点数固定，而第一隐含层节点数逐步增加时，DAE-ELM分类性能的变化并不是一个单调的过程，存在一个或多个最优节点数，使得DAE-ELM分类错误率最低，如图7中隐含层节点数为200时。

当固定DAE-ELM的第一隐含层节点数为200后，进行DAE-ELM与ELM、K-ELM（Kernel ELM）[3]、PCA-ELM（Principal Component Analysis ELM）[22]算法的性能对比分析，观察各算法性能随隐含层节点数增加的变化情况。其中各算法参数设定为：K-ELM中KernelParam=0.1，PCA-ELM取前200维，其累计贡献率为96.89%，DAE-AE参数不变。不同算法的分类性能如图8所示。

观察图8可以发现，DAE-ELM算法性能在数据集未添加噪声的情况下，性能优于其他ELM算法，尤其在隐含层节点数低于1500时，性能优势明显。DAE-ELM分类错误率的降低主要有以下三点原因：1）与其他ELM相比，DAE-ELM由DAE生成ELM的输入权值与隐含层参数，避免了算法随机赋值的偶然性，提高了算法的鲁棒性，且比K-ELM采用核函数方法优化隐含层输出的方法更优;2）与ELM，K-ELM相比，DAE-ELM中DAE起到了特征降维的作用，有利于剔除数据中的冗余信息，将其作为输入数据，有利于提高ELM性能;3）与PCA-ELM相比，DAE的特征降维并不是将部分特征删除，而是发掘特征间的关联信息，将其抽象为更高级的特征，这些高级抽象特征更能体现事物的本质，有利于降低分类错误率。

3.3.2 退化率影响实验

退化率是DAE中的重要参数，它直接关系到编码器所提取的高级抽象特征，进而影响算法性能。在本次实验中，将着重分析不同退化率对输入样本、特征提取、分类性能的影响。

实验数据为未加噪声MNIST数据，DAE-ELM网络结构为784-200-1500-10，退化率v={0，0.1，0.4}，其余参数与3.3.1节实验相同（当v=0时，DAE-ELM算法即为AE-ELM[23]算法）。当v取不同值，输入样本、输入权值如图9～10所示。

由图9可以看出，随着退化率v的增加，经退化后的样本所加入的噪声越多，样本失真越严重。但从图10可以发现，当v=0.1时，输入权值较未经过退化情况下的更清晰分明，这是因为经过退化后，为使得重构误差函数达到最小值，DAE必须尽可能地发掘更本质、鲁棒的高级抽象特征，促进其对重构数据的作用，进而降低次要特征的影响。发掘更加本质、鲁棒的高级抽象特征对模型性能有促进作用。当v=0.4时，过高的退化率导致样本失真严重，输入权值更加模糊，使得提取的特征不能很好地识别不同类别样本的差异，这对模型是不利的。所以，将模型退化率控制在合理范围内，这对DAE-ELM模型具有重要意义。

为进一步确定合理的退化率范围，接下来测试当其余参数不变，v={0，0.05，0.1，…，0.5}范围内对MNIST数据集的分类性能，其测试结果如图11所示。

从图11可以发现，当v≤0.25时，DAE-ELM分类错误率处于一个震荡过程，且v=0.1时，训练与测试分类错误率均达到最低值;当v>0.25时，错误率明显上升。由此可见，针对MNIST数据集，DAE-ELM中v的合理范围为[0，0.25]，最佳取值为0.1。模型性能变化大致分为三个阶段：1）当v<0.1时，分类错误率先上升后下降，这是因为提取高级抽象特征对于模型性能的促进作用与退化过程相比是滞后的，当v较低时，高级特征的促进作用弱于退化过程的抑制作用，随着v的增加，促进作用增加并强于抑制作用，模型性能逐渐提高，直到v取到最优值，模型性能达到最佳。2）当0.1≤v≤0.25時，高级抽象特征的促进作用与退化过程的抑制作用不相上下，模型性能无明显变化。3）当v>0.25时，模型性能大幅度下降，这是因为退化过程造成失真严重，以至于提取的特征并不能很好表示原始样本，从而影响模型性能。所以，对样本数据进行合理范围内的退化有助于提升模型性能。

3.3.3 多算法性能对比分析

为验证DAE-ELM的综合性能，在本节实验中，将采用对上述4个数据集及其分别添加10%高斯白噪声与10%椒盐噪声后的8个数据集，共12个数据集进行DAE-ELM与其他算法的性能比较。其中ELM、PCA-ELM、SAA-2[15]、DAE-ELM网络结构分别为：784-1500-X，784-1500-X，784-200-200-X（为重复实验后性能最佳的结构），784-200-1500-X，其中X为类别数。各算法其余参数与实验1中相同（SAA-2参数与DAE-ELM相同）。各算法分类错误率如表3所示。

由表3可以发现，当隐含层节点数较少时，绝大多数数据集下DAE-ELM的分类错误率皆低于其余算法，且加入噪声对DAE-ELM性能的影响也较弱。在不含噪声影响下，DAE-ELM相较于ELM、PCA-ELM、SAA-2算法，其分类错误率在MNIST数据集中至少下降了5.6%，在Fashion MNIST数据集中至少下降了3.0%，在Rectangles数据集中至少下降了2.0%，在Convex数据集中至少下降了12.7%。

性能分析如下：1）DAE-ELM性能优于ELM、PCA-ELM，是因为DAE-ELM避免了隐含层随机赋值，且其提取特征并不是舍弃部分特征，而是将其融合为更能体现数据本质、更具鲁棒性的高级抽象低维特征。2）DAE-ELM性能优于SAA-2，一方面是因为ELM具有一致逼近性，随着隐含层节点数的增加，能逼近任意函数;另一方面是因为DAE在AE中加入的退化过程使得提取的高级抽象特征更具代表性和鲁棒性。3）但在个别含噪声数据中，PCA-ELM性能优于DAE-ELM，其原因可能是因为PCA在去掉部分维度时，将包含其中的噪声一并去除，大幅度减少了噪声对PCA-ELM性能的影响。

4 结语

针对ELM隐含层参数随机赋值降低算法鲁棒性以及传统ELM处理高维含噪数据性能欠佳的问题，本文提出了基于去噪自编码器的极限学习机（DAE-ELM）算法。首先通过堆叠的DAE分别产生ELM输入数据、隐含层参数，然后通过ELM算法求解隐含层输出权值，完成对网络的训练。实验结果表明，不管高维数据是否含有一定噪声，DAE-ELM算法相较传统ELM算法与自编码器算法，其分类错误率得到了较大的下降，同时提供了拓宽ELM与深度学习算法结合的思路。但DAE-ELM为保持良好的泛化能力，仍然需要一定量的隐含层节点数作为支撑，这需要今后进一步的研究加以改善。

参考文献 （References）

[1] HUANG G B， ZHU Q Y， SIEW C K. Extreme learning machine： theory and applications [J]. Neurocomputing， 2006， 70（1/2/3）： 489-501.

[2] HUANG G B， CHEN L， SIEW C K. Universal approximation using incremental constructive feedforward networks with random hidden nodes [J]. IEEE Transactions on Neural Networks， 2006， 17（4）： 879-892.

[3] HUANG G B， ZHOU H M， DING X J， et al. Extreme learning machine for regression and multiclass classification [J]. IEEE Transactions on Systems， Man， and Cybernetics， Part B： Cybernetics， 2012， 42（2）： 513-529.

[4] ZONG W W， HUANG G B， CHEN Y Q. Weighted extreme learning machine for imbalance learning [J]. Neurocomputing， 2013， 101： 229-242.

[5] LIANG N Y， HUANG G B， SARATCHANDRAN P， et al. A fast and accurate online sequential learning algorithm for feedforward networks [J]. IEEE Transactions on Neural Networks， 2006， 17（6）： 1411-1423.

[6] LAN Y， HU Z J， SOH Y C， et al. An extreme learning machine approach for speaker recognition [J]. Neural Computing and Applications， 2013， 22（3/4）： 417-425.

[7] 王光華，李素梅，朱丹，等.极端学习机在立体图像质量客观评价中的应用[J].光电子·激光，2014，25（9）：1837-1842.（WANG G H， LI S M， ZHU D， et al. Application of extreme learning machine in objective stereoscopic image quality assessment [J]. Journal of Optoelectronics·Laser， 2014， 25（9）： 1837-1842.）

[8] XU Y， DAI Y Y， DONG Z Y， et al. Extreme learning machine-based predictor for real-time frequency stability assessment of electric power systems [J]. Neural Computing and Applications， 2013， 22（3/4）： 501-508.

[9] HORATA P， CHIEWCHANWATTANA S， SUNAT K. Robust extreme learning machine [J]. Neurocomputing， 2013， 102： 31-44.

[10] RONG H J， ONG Y S， TAN A H， et al. A fast pruned-extreme learning machine for classification problem [J]. Neurocomputing， 2008， 72（1/2/3）： 359-366.

[11] CHARAMA L L， ZHOU H， HUANG G B. Representational learning with ELMs for big data [J]. IEEE Intelligent Systems， 2013， 28（6）： 31-34.

[12] TANG J X， DENG C W， HUANG G B. Extreme learning machine for multilayer perceptron [J]. IEEE Transactions on Neural Networks and Learning Systems， 2016， 27（4）： 809-821

[13] ZHU W T， MIAO J， QING L Y， et al. Hierarchical extreme learning machine for unsupervised representation learning [C]//Proceedings of the 2015 International Joint Conference on Neural Networks. Piscataway， NJ： IEEE， 2015： 1-8.

[14] YANG Y M， WU Q M J. Multilayer extreme learning machine with subnetwork nodes for representation learning [J].IEEE Transactions on Cybernetics， 2016， 46（11）： 2570-2583.

[15] VINCENT P， LAROCHELLE H， BENGIO Y， et al. Extracting and composing robust features with denoising autoencoders [C]// ICML 2008： Proceedings of the 25th International Conference on Machine Learning. New York： ACM， 2008： 1096-1103.

[16] HUANG G， HUANG G B， SONG S J， et al. Trends in extreme learning machines： a review [J]. Neural Networks， 2015， 61： 32-48.

[17] 郭旭东，李小敏，敬如雪，等.基于改进的稀疏去噪自编码器的入侵检测[J].计算机应用，2019，39 （3）：769-773.（GUO X D， LI X M， JING R X， et al. Intrusion detection based on improved sparse denoising autoencoder [J]. Journal of Computer Applications， 2019， 39 （3）： 769-773.）

[18] LECUN Y， BOTTOU L， BENGIO Y， et al. Gradient-based learning applied to document recognition [J].Proceedings of the IEEE， 1998， 86（11）： 2278-2324.

[19] XIAO H， RASUL K， VOLLGRAF R. Fashion-MNIST： a novel image dataset for benchmarking machine learning algorithms [EB/OL]. [2018-09-15]. https：//arxiv.org/pdf/1708.07747.pdf.

[20] ERHAN D. RectanglesData [DB/OL]. [2018-09-15]. http：//www.iro.umontreal.ca/～lisa/twiki/bin/view.cgi/Public/RectanglesData.

[21] ERHAN D. Recognition of convex sets [DB/OL]. [2018-09-15]. http：//www.iro.umontreal.ca/～lisa/twiki/bin/view.cgi/Public/ConvexNonConvex.

[22] 肖冬，王繼春，潘孝礼，等.基于改进PCA-ELM方法的穿孔机导盘转速测量[J].控制理论与应用，2010，27（1）：19-24.（XIAO D， WANG J C， PAN X L， et al. Modeling and control of guide-disk speed of rotary piercer [J]. Control Theory & Applications， 2017， 27（1）： 19-24.）

[23] 马萌萌.基于深度学习的极限学习机算法研究[D].青岛： 中国海洋大学， 2015：28-30.（MA M M. Research on Extreme learning machine algorithm based on deep learning [D]. Qingdao： Ocean University of China， 2015： 28-30.）