浅谈深度教学中小学数学“U型学习”模式

董艳

我们当下的数学课堂教学，对知识的积累、技巧的训练等工具性价值过分关注，压抑了学生学习的主动性与探索性，使得他们对数学的情感淡漠了，对数学的兴趣被扼杀了。缺少了对思想的追寻，忽视了思维的启迪，丧失了方法的引领，我们的课堂能够教给学生什么？只能是无意义、无思想、无涵养的符号。

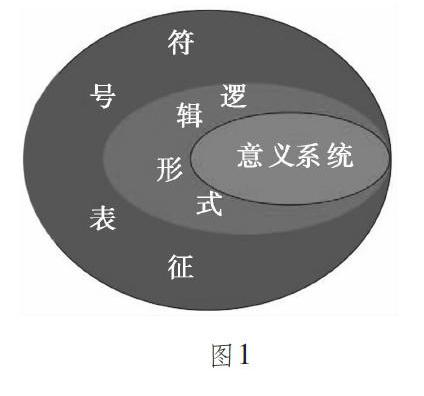
深度教学旨在克服教学过程中表面、表层、表演的局限，引导学生深层、深刻、深度学习。深度教学改革站在知识的教育学立场重新审视知识的教育学意义，揭示知识的符号表征、逻辑形式和意义系统（图1），提倡通过课程的过程性规约来实现知识的教育价值，正好契合了核心素养培养的内在要求。

学生学习经历的不规范、不完整、不丰富，实质上反映了一线教师普遍存在的“忽视教学的过程价值”的弊端。即便强调“把时间还给学生”，也仅仅是强调让学生在时间上自主，却呈现出方法上的失控、知识理解上的单向度。

从书本知识到个人知识，学生究竟经历了一个怎样的过程？书本具有不可教性，不能直接进行传授，而需要让学习者经历一个复杂的过程，即知识的学习需要经过“还原和下沉”“体验与探究”“反思与上浮”的过程。这一学习过程恰似一个“U型”。

“U型学习”的学习形态充分体现了学生学习的主体性，它保证了学生充分的学习投入或学习参与，实现了学习过程的完整性、规范性和丰富性，从而充分发挥了教学的过程价值。

“U型学习”的第一个环节是“下沉与还原”。在数学学习中，学生首先要将课本知识还原，还原为“儿童已有的知识背景”，还原为“活动经验”，还原的过程即知识的“下沉”过程。“下沉”环节是对知识进行表征化、表象化和具象化的过程。“下沉”一方面有助于学生理解知识的背景和现象，另一方面有助于建立起书本知识与学生个人经验的关联性，从而增强学生对知识的理解。大多“去情境”教学的局限就在于去掉了知识的具象化与表征化过程。

“U型学习”的第二个环节是“体验与探究”。这一过程是“U型学习”的底部，是对知识进行自我加工的过程，是对知识理解、对话、运用的过程。从学习过程的连续性和整体性来看，“体验与探究”环节是最复杂、最深刻的，是学生真正把知识符号转化为逻辑形式的重要步骤。大多数“去过程”教学的局限性就在于简化、压缩了这一复杂且深刻的必要过程，从而极大地减损了整体目标的达成。

U型学习的第三个环节是“反思与上浮”，即学生反思性和批判性思维的形成过程。经过反思性思维，将经过自我加工的书本知识进行个人意义的升华和表达，书本知识才真正变成学生自己理解的东西，即所谓“个人知识”，是对书本知识的个人化理解、自我建构并获得知识的意义增值。

笔者在“除数是两位数的除法”练习课上，发现学生会计算“612÷78”后，却不会计算除数是一位数的除法“612÷8”了（图2）。看来，学生只是机械记住了教师说的“把除数看成与之接近的整十数来试商”。至于“为什么要这样做？”“它与前面的旧知识有着怎样的联系？”学生没有深思，只是“老师让怎么做，就怎么做”。由此可见，如果我们的教学省去了“U型学习”这一重要过程，学生所获得的知识永远只能停留在对书本知识的简单占有层面，学生的数学素养与关键能力就难以达成了。

一、掠去表象，突出本源，“U型学习”实现理解性学习

面对未知世界的学习，学生必须获得对概念更深层次的理解。有研究表明，与把知识作为孤立的事实来接受和记忆的浅层学习不同，深度教学中的“U型学习”强调理解与批判地接受知识。

在小学数学中，一些性质、规律、法则背后常常蕴含着更为一般的原理，它們是一般原理在特定情境中的特殊表现。而这些知识本质又可以追溯到学生已有或熟知的经验与观念。在“下沉与还原”中，教师应当运用多种方法探明学生对于将要学习的概念或原理的前理解，并运用相应方法解构学生的前概念。

当学生能熟背结论与方法时，教师应当思索——“知道事实是否真正理解”“会背概念是否真正理解”“会做题是否真正理解”。例如，“角的度量”这一课历来是小学数学测量教学中的重难点。通常教师会教给学生量角的方法，即“点对点，边对边，再定内外圈”，最后进行反复练习。但从实际情况看，效果并不理想。部分学生要么总是不会，要么测量的方法单一。其实，与测量长度、面积和重量一样，度量的本质是相同的，即看度量的对象含有多少个单位。在学生“探究和加工”的学习过程中，把握数学本质联系是解决问题的法宝。可谓“越高级越简单，越真理越明了”。

教学过程绝不是简单地将书本知识原封不动地投射到学生脑海里的过程，更不是对书本知识的简单复制的过程。如若在课堂学习中投入知识的文化背景，学生获得的就不仅仅是对知识的符号认知而是对知识的文化理解。如若投入学生的生活经验，便能在知识的理解过程中生成新的想象或画面。

“U型学习”强调教师在知识教学过程中有效进行背景导入、经验导入、文化导入，可以提高学生对知识的理解水平并促进知识的转化，进而促进知识从“表层符号学习”进入“知识内在的逻辑形式和意义领域”。

二、抓住关联，注重综合，“U型学习”实现建构性学习

教育理论和实践都充分证明：学习一个数学概念、原理、法则，如果在心理上能组织起适当的、有效的认知结构，并使之成为个人内部的知识网络的一部分，那么学生才会产生他们自己的数学理解。

数学知识体系是以基础性、决定性的概念、原理、法则等为地基，构造出整座“数学大厦”的。学生探究数学知识时，不但需要一些基础性、常规性知识来驱动，更需要从数学整体结构乃至本源把握数学知识的前后联系。“U型学习”强调从知识的内在结构出发，通过多种方式，寻求知识的连接与构建，在不同模型间实现迁移，以利于学生形成开放的知识结构。

如“三位数乘两位数的笔算”学习中，学生从“两、三位数乘一位数笔算”过渡到“两位数乘两位数的笔算”，再到“三位数乘两位数的笔算”，从知识层面来说是纵向的统一体系上的知识点，从经验层面来说学生有可以解决问题的口算、估算与笔算的经验。课堂上，在经历了笔算探究的整个过程之后，教师引导学生经历从“表内乘法”到“三位数乘两位数的笔算”整个知识体系生长的过程。全课尾声，教师还让学生猜一猜，关于“笔算乘法”，小学阶段还会研究什么问题？将知识进行系统整理，把零碎的知识点串联成一条线，让学生感知数学的学习是螺旋上升的系统。而在学生开始漫无边际地想到“四位数乘三位数”与“多位数乘多位数”时，教师指出：“在整数的笔算乘法中，小学阶段只研究到此。那遇到位数更多的乘法怎么办呢？”学生顿悟：笔算乘法的核心就是根据“乘法的意义”，利用“数的组成”及“位值原则”，一切乘法问题均可迎刃而解。

作为教师，要有一定的高度和眼界，注重教学内容的丰富、关联与综合。通过知识的结构化组织、模块化架构和网络化呈现，丰富学生的认知结构，让学生有意识地建立联系，体会建构的意义，外化思维过程，从碎片化学习向立体式学习转型。

基于此，实现“U型学习”既需要教师对知识进行合理加工、有效组织和多样化呈现，同时还需要学生善于运用学习策略，深入理解知识，对知识进行积极建构，并内化到个体的认知结构之中。

三、渗透方法，提升思考，“U型学习”实现反思性学习

弗赖登塔尔提出，数学思维的发展主要是指由较低层次上升到更高层次。但是，只要儿童没能对自己的活动进行反思，他就达不到高级的层次。当前的数学课堂，教师注重引导学生通过活动来学习，注重理解、对话等学习形式，但由于忽视深度体验及反思感悟，完整的学习经历中缺少“反思与建构”的过程，学习活动变得虎头蛇尾。诸如此类，自然不能达成数学知识、数学经验、数学思想和数学品格等多维目标。

“U型学习”中的“反思与上浮”，不是简单的“自我纠错”，也不应仅仅理解为“事后反省”，而是应该贯穿于学习经历的全过程，应当成为主体思维活动十分重要的一个组成部分或基本特征。

教学的高境界，不是“教会”，而是让学生自己“悟得”。培养学生的反思性思维，需要立足学生高阶思维的形成。教师应该将高阶思维的发展作为教学目标的一条暗线伴随课堂教学始终，提升学生的理解、反思和批判能力，强调学生对知识的具体内容、知识之间的内在逻辑关系的梳理和理解，进而锻造学生思维品质，实现深度教学，促进学生核心素养的发展。

一个充溢着数学思考的学习过程，彰显的就是数学思考本身的内在力量。前期看似有些“繁琐”，长期来看却是“简单”，真正实现“以一驭多”。随着数学思考力量的不断积累与壮大，数学学习将变得越来越有味道、越来越有吸引力。

综上所述，通过坚持实施“U型学习”模式教学，真正实现“无论学生将来从事什么工作，深深铭刻在心的理性的精神、严谨的思维方法、看问题的着眼点等，可以随时随地发生作用，使他们终身受益”。这个过程不但是培养学生数学品格和关键能力的过程，更是深化小学数学教师对课程理解的过程，是实现师生共同成长的过程。

（作者单位：华中师范大学附属小学）