异构无线网络多用户多业务接入中多目标优化控制方法研究

董晓庆，程良伦，陈洪财，郑耿忠，谢森林*

(1. 广东工业大学 计算机学院，广东 广州 510006 2. 韩山师范学院 物理与电子工程学院，广东 潮州 521041)

1 引 言

用户业务量及用户终端数量近年来呈爆发性增长态势，单一通信网络已无法满足用户的需求，未来的无线通信网络必然是多网络共存、融合、优势互补，这也是下一代无线通信网络的发展趋势[1-2]。多模终端可通过多无线电接入技术选择不同的接入网络(比如蜂窝网络、无线局域网络(Wireless Local Area Networks，WLAN)、全球互通微波访问网络(Worldwide Interoperability for Microwave Access，WiMax)等)进行数据传输。在异构网络重叠覆盖多用户多业务共存环境下，如何为用户选择合适的接入网络及分配带宽，以保障网络系统可靠性并满足不同用户的服务需求，已成为研究热点[3-4]。

目前异构无线网络的网络接入及资源分配方面已取得一些研究成果。文献[5]针对带宽资源受限条件下如何选择接入网络以最大化传输速率的问题，提出了一种基于牛顿迭代算法的网络选择方法。该方法首先分别以信息传输速率最大化为目标及带宽资源受限为约束对网络接入问题进行建模，然后通过牛顿迭代算法求得信息传输速率最大化的接入网络及在该网络中所需带宽资源理论值，把用户分配到理论值与实际带宽需求差值最小的网络中，以提高带宽资源的利用率。文献[6]提出了一种基于离散粒子群的网络选择接入的多目标优化方法，该方法首先通过惩罚函数法将多优化目标转换为单目标，然后利用离散粒子群算法求解，提高了用户满意度。文献[7]分析了无线异构网络中用户总信息传输速率与网络接入及带宽分配的关系，将复杂的多链路动态接入建模为系统传输速率最大化问题，提出一种支持多链路接入的多阶段求解方法，从而最大化总用户信息传输速率。文献[5-7]把提高信息传输速率作为目标，但忽略了网络间的负载差异，易造成网络间负载不均衡。文献[8]利用博弈理论构建了异构无线网络中的带宽资源分配及用户终端网络关联理论模型，提出了可靠通信的接入控制方法以降低用户接入阻塞率，但非合作博弈中纳什均衡的存在性和唯一性难以确定，求解最佳方案难度较大。文献[9]针对负载均衡问题，通过构建与实际流量模型相符的网络节点分簇拓扑结构，提出了一种基于梯度的负载均衡非均匀分簇方法，在一定程度上提高了负载均衡并缓解网络拥塞情况。文献[10]分别分析了用户的资源占用模型、阻塞率模型及网络负载模型，并建模了总资源占用最小化、业务阻塞率最低及网络负载最均衡的多目标优化模型，并通过最大化满意度将多目标转化为单目标，最后利用遗传算法求解，但该方法在网络负载较重时，用户接入阻塞率偏高。文献[11]针对现有异构无线网络接入多目标优化方法大多将多目标转化为单目标，没有充分考虑各目标相对关系的问题， 提出一种基于分解的多目标进化算法，然后通过非支配排序得到最优网络接入方案，在用户阻塞率、负载均衡及资源占用取得较好的折中效果。文献[9-11]从网络的角度对系统性能进行优化，但忽略了用户的速率需求。

综上所述，在异构无线网络多用户多业务接入环境下，目前在网络侧的负载均衡、阻塞率方面及用户侧的速率需求方面均取得一定的研究成果，但联合考虑网络负载均衡及用户速率需求的研究成果还较少。因此，为保证系统通信速率及网络间的负载均衡，本文以系统通信速率及负载均衡为目标，构建多目标优化控制模型，提出一种基于多目标优化的业务接入控制算法，以满足用户的服务质量需求及保障网络的可靠性。

2 网络模型及问题定义

2.1 网络模型

如图1所示，假设存在N个异构无线网络重叠覆盖(包括蜂窝网络、WiMax及WLAN)，M个多模用户终端可以根据自身服务质量(Quality of Service，QoS)需求及网络效益选择接入任一网络。载波传输方案采用基于多用户正交频分复用技术(Orthogonal Frequency Division Multiplexing，OFDM)[12-13]，基本的资源分配单元为一个子时隙和一个子信道构成的二维资源单元( Two-dimensional Resource Unit，TRU)[10,14]，网络k( 1≤k≤N) 能提供的TRU资源数Tk为：

(1)

其中，Nk为网络k的子载波总数，Fk为每个子信道包含子载波个数，TSk为每帧的帧长，SPk为OFDM的符号周期，Sk为每个时隙包含的 符号个数。

令Xjk表示用户j的网络接入情况，若用户接入网络k，则Xjk等于1，否则为0。因此用户终端的网络接入情况可表示为一个M×N的0/1二维矩阵，如公式(2)。

(2)

2.1.1 系统负载率模型

设业务j接入网络k后，需要网络提供的TRU资源数为tjk，那么网络k分配给所有用户的资源数量为：

(3)

其中，Bk为用户所占用的网络资源。根据公式(1)中的网络可提供资源，可推导出网络k的负载率为：

(4)

2.1.2 传输速率模型

网络k的信息传输速率由接入该网中的所有用户终端决定，根据香农定理，网络k的信息传输速率可表示为：

(5)

其中，bjk表示用户j在网络k中分配到的信道带宽，Sjk、Njk分别表示信号功率及噪声功率，ωjk表示用户j在网络k中的效益因子。

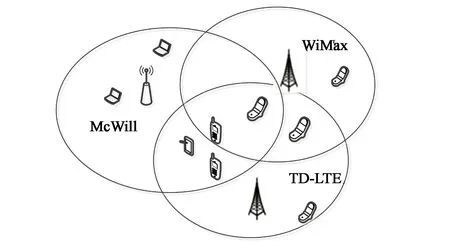
图1 重叠覆盖的异构无线网络Fig.1 Overlapping heterogeneous wireless networks

2.2 问题定义

用户的网络接入及带宽分配影响到系统的传输速率及网络间负载，本文从整个异构无线网络的角度，通过为用户选择合理的接入网络及资源分配，使系统获得最大传输速率并保持网络间的负载均衡。因此，本文将目标函数建模为最均衡网络负载及最大化系统传输速率。

本文以负载率方差衡量各异构网络间负载均衡程度，负载率方差最小化表征负载最均衡，由2.1节中的负载率模型，负载最均衡可表示如下：

(6)

从整个网络的角度，系统传输速率为各个异构网络获得的传输速率之和，根据公式(5)网络k的传输速率，系统传输速率最大化可表示如下：

(7)

由公式(6)、(7)，可以推导出以系统传输速率最大化及网络负载最均衡为目标，以带宽资源限制作为约束条件的数学模型，具体如下：

(8)

其中约束条件1表示接入网络k的所有用户占用资源总和不得超过网络k所能提供的总资源，约束条件3表示每个用户最多只能接入一个网络。该优化模型既考虑了用户的传输速率需求，同时保证了网络间的负载均衡。

3 接入控制方法

本文在带宽资源受限条件下，以网络负载最均衡及系统传输速率最大化为目标，构建了如公式(8)所示的多目标优化模型。对于约束条件的多目标优化问题，难以利用多项式时间算法求解，因此，本文基于非支配排序遗传算法NSGA-Ⅱ求解复杂的资源分配及网络接入问题。

NSGA-Ⅱ利用强大的全局搜索能力较好地解决了多目标优化问题，其具有进化操作规则的概率性、充分利用适应值函数而不需要其它先验知识等特点，且在解空间中沿多个方向并行搜索，不易陷入局部最优，适合求解传统方法难以解决的复杂优化问题。但由于非支配排序算法求得的一组最优帕累托解集中不存在一个可使所有优化目标同时最优的解，而本文需要求得唯一方案以确定网络接入及带宽资源分配，因此本文对经典的非支配排序算法进行改进，提出了一种折中的决策精选策略对得到的帕累托解进行排序。在得到帕累托解集后，该方法通过计算个体各个优化目标值与对应最优值的归一化趋近度，一个优化目标对应一个趋近度，并根据优化目标的重要性赋予一定的权重；最后将同一个体所有优化目标对应的趋近度相加以表征该个体对最优个体的趋近度，趋近度越小表示越接近最优值，并选择趋近度最小的个体作为本文的解。同时，本文对NSGA-II算法进行适应性处理，以解决复杂的资源分配及网络接入问题。下面将给出本文改进的非支配排序算法关键步骤。

3.1 个体编码

个体表示问题的解决方案，给出用户终端的接入网络及选择的带宽资源，一定数量的个体组成一个种群。基于此，本文采用二进制方式对个体进行编码，个体中基因对应用户终端，基因的值表示用户接入的网络及分配到的资源，所以m个用户，需要m个基因。下面给出一个个体实例，假设在一个由3个异构无线网络重叠覆盖场景中，每个网络有10个TRU资源，网络中有8个用户申请接入，那么需要8个基因表示8个用户的资源分配情况，每个基因需要用2位表示接入的网络，4位表示所选TRU资源，共48位组成了一个个体，其编码方案如图2所示。

图2 个体编码方式Fig.2 Chromosome coding

3.2 非支配排序

本文的优化目标包括传输速率最大化及负载最均衡，1个个体确定1个网络接入、资源分配方案及对应的系统传输速率、网络间负载方差目标值，本文基于传输速率及负载方差目标值进行非支配排序，排序方法如下：(1)目标值处理：同时考虑网络资源约束及终端接入约束，对于符合约束条件的个体，取其目标值进行排序，否则令其传输速率为0、网络间负载方差为最大值，以淘汰不符合约束条件的个体；(2)非支配排序：设a和b为种群中任意2个不同个体，如果满足a个体的目标值都不比b差，且至少存在一个目标值优于个体b，则称a为非支配解，b被a所支配；如果两个个体目标值相等或互有优劣，则a、b互不支配，分配在同一层级。

3.3 遗传操作

3.4 决策精选

利用非支配排序算法求得一组最优帕累托解，该组解集中不存在一个可使所有优化目标同时最优的解，而本文需要求得唯一方案以确定网络接入及带宽资源分配，因此本文提出了一种折中的决策精选策略，该策略如式(9)所示：

(9)

综上所述，本文基于改进的非支配排序方法对染色体进行排序，再利用遗传操作实现染色体的迭代更新，最后通过决策精选策略优选出1个折中优化方案。

4 实验结果分析

4.1 实验参数设置

对于优化问题，采用凸优化理论求解及利用启发式智能算法求解是两类常用的解决方法，文献[5]基于牛顿迭代算法(Newton Iteration，NI)的网络选择策略及文献[10]中的多目标优化控制(Multi-objective Optimization Control，MOC)算法是这两类方法的典型代表。因此，本章通过仿真将本文基于NSGA-Ⅱ的算法与文献[5]的NI算法及文献[10]的MOC算法进行对比分析，以测试算法的有效性。假设3 种目前常见的网络重叠覆盖，如图 1 所示，网络 1、网络 2、网络 3 分别表示WiMax、多载波无线信息本地环路网络(Multi-Carrier Wireless Information Local Loop，McWiLL)和分时长期演进网络(Time Division Long Term Evolution，TD-LTE)，网络半径分别为 3，3，1.5 km，基站位置随机生成。WiMax和TD-LTE的网络参数设置同文献[15]，McWiLL 网络参数设置同文献[16]。

假设各异构无线网络中初始业务分布随机产生，同时随机生成100 个新到通信业务，其中实时业务带宽需求随机均匀分布在 50～200kb/s，非实时业务分布在40～140 kb/s，两种业务各约占50%。本文所提算法参数如下：初始种群随机生成，种群规模P=60，交叉概率pc为0.9，变异概率(pm)为0.1，迭代次数为200。

4.2 算法性能分析

下面分别对算法的负载率均衡程度及传输速率进行对比分析。

4.2.1 归一化负载率对比

图3给出了本文所提算法在3个网络中的负载均衡状况，如图所示，随着用户数量的增加，用户占用网络资源相应增加，3个网络负载率均上升；在负载率上升的过程中，3条曲线始终保持缠绕，在不同用户数下负载率差距较小，网络间负载始终较为均衡。

图3 本文算法的归一化负载Fig.3 Normalized load of the proposed algorithm

下面进一步将本文所提算法与其他两种算法的归一化负载进行对比。如图4(a)所示，本文算法与MOC算法的网络负载率均随着用户数的增加而增加，且各网络负载曲线比较集中，表明网络间保持较均衡的状态，因为两种算法都将网络间的负载方差最小化作为优化目标，使各用户均衡地接入到各个网络，较好地实现了负载均衡；同时，可看出MOC算法的负载率稍低于本文算法，因为MOC算法将占用最少资源作为优化目标之一。图4(b)给出了本文算法与基于NI算法的负载对比，如图所示，NI方法在不同用户数下各曲线较为松散，网络间负载差距较大，且负载率相比本文算法大，因为NI方法将传输速率最大化作为唯一目标，始终选择使传输速率最大化的接入网络，而忽视了网络间的负载均衡。

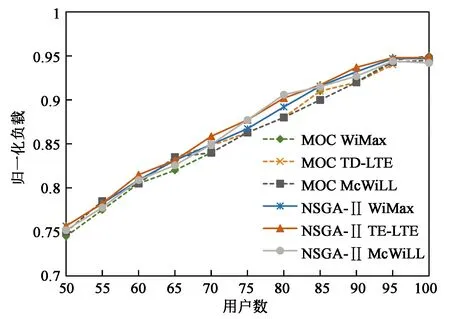
(a)与MOC算法对比(a)Comparison with MOC algorithm

(b) 与NI算法对比(b) Comparison with NI algorithm图4 归一化负载对比Fig.4 Normalized load comparison

4.2.2 传输速率对比

图5比较了算法在不同接入用户数下的传输速率。如图所示，3种算法在接入用户数小于85时，系统信息传输速率与用户数呈线性增长关系，在大于85时，传输速率增长平缓而趋于稳定。同时，由于MOC算法没有考虑传输速率，其各用户数下的传输速率均明显低于其它两种算法。本文算法与NI算法都将传输速率最大化作为优化目标之一，令用户接入信道条件较好的网络，取得了较高的传输速率。

图5 传输速率对比Fig.5 Transmission ratecomparison

由上述实验可知，采用本文提出的基于NSGA-Ⅱ算法的业务接入控制策略，在保持网络间负载均衡的情况下，获得了较高的传输速率，显示出本文所提方法的有效性。

5 结 论

本文针对异构网络多用户多业务共存环境下，用户期望接入最优网络以获取最大的信息传输速率，导致网络负载不均衡的问题，构建了信息传输速率最大化及网络负载最均衡的双目标优化模型，并基于NSGA-Ⅱ多目标优化算法求解该复杂的业务接入问题。实验结果表明，与已有的网络接入及资源分配方法相比，本文算法兼顾了用户的传输速率需求及系统间的负载均衡问题，在用户的QoS需求及网络系统性能间取得较好的均衡，具有一定的应用价值。