利用光反馈多模激光器结合滤波器产生平坦混沌*

李锟影 李璞3)† 郭晓敏 郭龑强 张建国 刘义铭 徐兵杰 王云才

1) (太原理工大学,新型传感器与智能控制教育部重点实验室,太原 030024)

2) (太原理工大学物理与光电工程学院,太原 030024)

3) (上海大学,特种光纤与光接入网省部共建重点实验室,上海 200444)

4) (中国电子科技集团公司第三十研究所,成都 610041)

5) (西南通信研究所,保密通信重点实验室,成都 610041)

1 引 言

光学混沌在通信领域潜在价值巨大,受到国内外学者的密切关注,已被广泛用作保密通信的载波信号[1],测距雷达或光时域反射仪的探测信号[2−4]以及密钥发生器的熵源信号[5−10].

近年来,光反馈激光器因宽带、大幅度及结构简单等特性,是最常用的混沌激光产生系统,其混沌的动态特性研究受到国内外学者的青睐.例如:2001年,Quay等[11]研究了垂直腔面发射激光器(VCSEL)在强光反馈下的混沌特性,并理论分析了激光光谱红移的机制; 2007年,Rontani等[12]研究了光反馈单模半导体激光器中反馈率对时延信息和弛豫振荡周期的作用; 2010年,夏光琼教授课题组[13]研究了双腔反馈混沌半导体(DFB)激光器的时延特征,且分析了弛豫振荡对时延抑制的影响; 2015年,潘炜教授课题组[14]实验和理论分析了两类光反馈DFB激光器的统计特性,并证实后处理技术可以改善混沌信号的动态特性; 2018年,Ahmad等[15]研究了交流耦合光反馈混沌半导体激光器的动力学特性,通过控制反馈强度,测试了混沌的不稳定性; 2018年,Grillot等[16]实验研究和对比了两种多模光反馈量子点激光器的动力学特性,并理论分析了外腔长度变化对混沌振荡的影响.

但受激光器弛豫振荡的影响,光反馈半导体激光器直接产生的混沌信号能量主要集中在高频弛豫振荡频率处,低频成分存在严重缺失.实际应用中信号探测/采集器件的响应通常表现为3 dB低通滤波特性,因此,混沌信号被利用的有效带宽实际上应是3 dB带宽.低频成分的缺失将局限混沌信号的能量利用率,制约混沌应用的相关性能(如混沌通信速率、密钥产生速率、测距雷达及光时域反射仪的测量精度和范围等).

针对低频成分的缺失问题,本课题组前期提出了光反馈单模混沌激光器结合延迟自干涉结构[17]、光外差结构[18]或光纤振荡环[19]结构的改善方案.但是,这些方案结构复杂,偏振敏感,易受环境影响.

本文提出一种结构简单、无低频成分缺失的宽带混沌激光产生方案.具体而言,我们实验上观察到法布里-珀罗(FP)半导体激光器在光反馈扰动下产生的多模混沌激光,经光带通滤波器后,将获得宽带平坦的单模混沌光.实验结果显示: 相较于多模混沌光,单模混沌光的低频振荡能量可提升25 dB; 经测量,该混沌激光的 3 dB 有效带宽可达6 GHz.进一步理论分析证明: 单模混沌信号中低频能量获得显著增加原因在于多模竞争,多模混沌信号低频部分能量会因模式竞争而被抵消.

2 实验装置

图1是光反馈FP激光器混沌频谱特性分析实验装置示意图.FP激光器(FP-LD)输出激光经偏振控制器(PC),被分光比为60︰40的光纤耦合器分为两路: 40%一路与光纤反射镜(FM)相连构成反馈腔,驱动FP激光器产生多模混沌激光; 所产生的多模混沌激光则由60%端口输出.

进而,多模混沌激光经掺铒光纤放大器(EDFA),在光带通滤波器(BPF)作用下,调谐不同的滤波中心,可以输出不同模式下的单模混沌信号.实验中,利用光谱分析仪 (OSA,YOKOGAWA,AQ6370C)观测混沌信号光谱,利用 12 GHz光电探测器 (PD,NEWPORT,1544B)与 26.5 GHz 频谱分析仪 (ESA,Agilent Technologies,N9020A)记录混沌信号频谱.

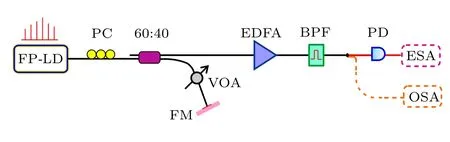
图1 基于光反馈FP激光器混沌频谱特性分析实验装置(FP-LD,法布里-珀罗激光二极管; PC,偏振控制器; VOA,可调光衰减器; FM,光纤反射镜; EDFA,掺铒光纤放大器;BPF,可调光滤波器; PD,光电探测器; ESA,频谱仪; OSA,光谱仪)Fig.1.Experimental setup for the RF spectrum analysis of optical feedback FP laser (FP-LD,Fabry-Perot laser diode;PC,polarization controller; VOA,variable optical attenuator; FM,fiber mirror; EDFA,erbium-doped fiber amplifier;BPF,optical bandpass filter; PD,photodetector; ESA,electrical spectrum analyzer; OSA,optical spectrum analyzer).

3 实验结果

图2 多模混沌激光特性实验结果 (a) 光谱; (b)频谱Fig.2.Characteristics of the multi-mode chaos: (a) Optical spectrum; (b) RF spectrum.

图2是实验记录的光反馈FP激光器直接输出多模混沌激光的光谱及频谱图.实验中,FP激光器偏置于1.5倍阈值电流(12 mA),反馈强度为20%.由图2(a)可观察到,FP激光器直接输出的多模混沌激光由分布在1535—1555 nm波长范围内的19个纵模共同组成,相邻纵模间隔约1.1 nm.为后续分析方便,我们将图2(a)中能量最高的纵模(中心波长1549.291 nm)定义为0模式,其两侧的 1550.390 nm和 1548.190 nm纵模分别定义为+1模式和–1模式; 其他纵模依次类推,分别定义为+2,–2,+3,–3 等.这里需要指出,实验中所用光谱仪的分辨率设置为了0.05 nm.图2(b)是利用频谱分析仪记录的混沌信号频谱图.实验中,频谱仪的分辨率带宽和视频带宽分别为1 MHz和1 kHz.很明显,多模混沌信号的能量主要集中在激光器弛豫振荡频率5 GHz附近,低频范围(0—5 GHz)内的能量存在大幅缺失,整个频谱呈现出单峰分布.这与常规的光反馈单模激光器(DFB或VCSEL)输出混沌信号频谱特低通滤波特性,这类混沌信号存在低频能量利用率低和3 dB有效带宽不足问题.

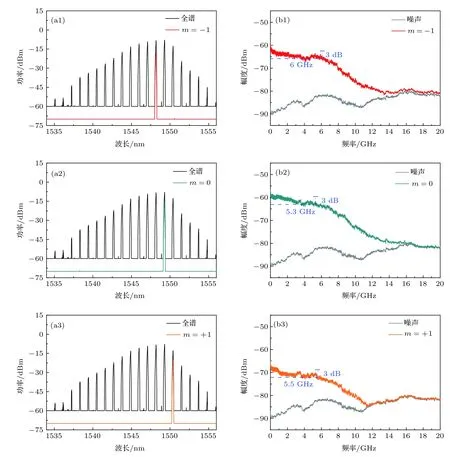
图3 m=–1,0,+1 模式下的单模混沌信号特性实验结果 (a1)—(a3)光谱; (b1)—(b3)频谱Fig.3.Characteristics of single-mode chaotic signals (m=–1,0,+1): (a1)−(a3) Optical spectra; (b1)−(b3) RF spectra.

为了解决低频能量缺失的问题,我们利用光带通滤波器BPF(滤波线宽设置为 0.27 nm)对混沌激光的 0,+1,–1 模式分别进行了滤波,并实验测量了所获得不同模式下单模混沌信号的光谱及频谱.图3(a1)—(a3)分别对应3个不同模式(m=–1,0,+1)的单模混沌信号光谱,而图3(b1)—(b3)则分别对应 3 个不同模式下 (m=–1,0,+1)的单模混沌信号频谱.与预期一致,m=0 模式处于整个光谱的中心位置[图3(a2)],因此,其在频谱上能量最高 (图3(b2)),其他两侧模式 (m=–1,+1)能量相对较低 (图3(b1),(b3)).但是,需要注意的是,不论是哪一个模式,相对于多模混沌信号,所有单模混沌信号在低频部分的能量均得到了大幅度提升,整个频谱更为平坦 (图3(b)).这里,能量提升是通过测量滤波前后混沌频谱在0 GHz处对应的功率值来确定的,以m=–1模式下输出的单模混沌信号频谱为例(图3(b1)): 经测量,其低频能量与原始多模混沌激光信号(图2(b))相比提升了 25 dB,3 dB 有效带宽可达 6 GHz.实验中,反馈强度是指反馈光强度与激光器输出光强度的比值.我们观察到在偏置电流一定时,当反馈强度大于2%,激光器开始进入混沌态; 当反馈强度到达20%时,混沌信号频谱带宽达到最大,且反馈强度改变时,滤波前后混沌带宽变化规律一致.这意味着只要将多模混沌激光器与相应滤波器简单结合,即可获得无低频成分缺失的宽带平坦混沌信号产生; 与在先技术[17−19]相比,本实验方案在系统复杂度上获得了显著改善.

4 理论分析结果

进一步,我们在理论上探究了光反馈多模激光器经过滤波之后获得的不同模式下的单模混沌信号低频成分能量得到显著提升的物理机制.具体而言,我们基于Lang-Kabayashi提出的理论模型,对光反馈多模激光器混沌动力学特性进行了数值模拟.如下[20,21]:

其中M表示多模激光器的模式总数,m对应多模激光器的第m个模式;E,F,N分别表示激光器的归一化振幅、相位和载流子数;D为激光器自身和外部反馈光的相位差,G为激光器增益,a表示线宽增强因子,g表示激光器内腔损耗系数,ge为载流子衰减系数,C为激光器工作时偏置电流系数(C=I/Ith,I为工作电流,Ith为阈值电流),t为光在腔内环行一周的时间,∆ωL=2π/τ表示为激光器纵模间隔,tt为反馈光延迟时间,kt为反馈光强度,Nth为阈值载流子数 (Nth=N0+g/gc,N0为透明载流子数,gc为微分增益系数),wc为增益峰值频率,Dwg为增益宽度,s为增益饱和系数;Fg(t)=是激光器自发辐射产生的噪声,其中,x(t)为高斯白噪声,b为自发辐射率.对应实验结果,本文将数值模拟的中心模式波长(m=0)对应在 1549 nm,纵模间隔为 1.1 nm,自发辐射噪声设置在–30 dB量级.具体参数如表1所列.

表1 光反馈 FP 激光器仿真参数Table 1.Simulation parameters of FP-LD with optical feedback.

图4(a)是模拟获得的15纵模光反馈FP激光器直接输出多模混沌激光的光谱.横坐标为光谱模式的相对波长,Dl=0 nm 对应的模式波长为1549 nm.光谱中可以清楚地看到有15个纵模状态存在,且纵模间隔在 1.1 nm.图4(b)是相应多模混沌信号的频谱图.与图2(b)对比可知: 本仿真结果和上述实验现象一致,多模混沌信号的大部分能量主要集中在弛豫振荡处,低频成分的能量存在缺失.

图5 为滤波后 3 个模式 (m=–1,0,+1)下单模混沌信号结果.图5(a1)—(a3)对应不同模式下的频谱图,可以发现中心模式(m=0)的能量最高,两侧纵模能量递减,这与实验结果(图3(b1)—(b3))一致.图5(b1)—(b3)为 FP 激光器在m=–1,0,+1模式下输出的单模混沌信号的时序图.从时序波动状态上可以看出,m=–1 和m=0 模式的时序起伏趋势相似,而m=–1 和m=+1 模式的时序起伏趋势在一定程度上相反,这意味着多模激光器模式因为共享载流子,相互之间存在着不同程度的竞争关系.

定量地,我们利用关联函数来进一步分析各纵模模式间的这种竞争关系.关联函数CC定义如下:

图4 多纵模光反馈 FP 激光器数值仿真结果 (a) 光谱 (M=15); (b) 频谱Fig.4.Numerical results of multi-mode FP-LD with optical feedback: (a) Optical spectrum (M=15); (b) power spectrum.

图5 光反馈多模激光器在 3 个模式 (m=–1,0,+1)下单模混沌信号的模拟结果 (a1)—(a3) 频谱; (b1)—(b3) 时序;(c1)—(c3) 互相关函数Fig.5.Simulation results of single-mode chaotic signals (m=–1,0,+1): (a1)−(a3) Power spectra; (b1)−(b3) time series; (c1)−(c3) cross-correlations.

式中Ei和Ej分别表示不同模式的复振幅.当关联函数的CC值越趋向于1时,表明模式间同相性越高; 当关联函数的CC值越趋向于–1时,表明模式间反相性越高.图5(c1)—(c3)是不同模式间的关联函数曲线.结果表明,FP激光器模式间同时存在着不同程度的同相和反相振荡关系.这证明了单模混沌信号中频谱低频能量获得显著增加的原因在于多纵模激光器的模式竞争.而所有模式共同作用下输出时的多模混沌信号在低频处的能量部分会因模式竞争关系而被抵消.

5 结 论

实验上通过对光反馈多模半导体激光器进行简单的滤波作用,可实现常规混沌信号低频能量的显著提升(25 dB),使混沌信号频谱相对平坦化,3 dB有效带宽得到大幅度增强(6 GHz).理论上,利用光反馈多模激光器数值模型,分析出滤波后单模混沌激光信号低频部分振荡能量的有效提升的本质原因在于多模激光器模式竞争.不同模式信号之间的反相关联,导致了所有模式共存时的多模混沌信号低频能量被互相抵消.

利用低成本多模激光器结合滤波器这种简单结构来产生频谱平坦、无低频能量缺失的宽带混沌信号,有利于提高混沌信号在实际应用中的能量利用率,对于混沌相关应用(如混沌通信、密钥产生、测距雷达及光时域反射仪等)具有重要意义.