基于袋鼠纠缠跳跃模型的量子状态自适应跳变通信策略*

聂敏 卫容宇† 杨光2) 张美玲 孙爱晶 裴昌幸

1) (西安邮电大学通信与信息工程学院,西安 710121)

2) (西北工业大学电子信息工程学院,西安 710072)

3) (西安电子科技大学,综合业务网国家重点实验室,西安 710071)

1 引 言

近年来,国内外关于自由空间量子通信的研究取得了巨大的成就.2010年,Jin 等[1]实现了 16 km自由空间量子隐形传态.2009年,奥地利科学院与维也纳大学通过实验演示了纠缠光子在144 km自由空间链路上的成功传输[2].2012年,Ma 等[3]进行了超过143 km的自由空间量子隐形传态实验并取得成功.Wang等[4]也于2013年完成了百公里级星地量子衰减信道的自由空间量子通信实验,2015年成功实现了多自由度的量子隐形传态[5].2016年,“墨子号”量子卫星成功发射,为全球量子通信网络的构建提供了理论和实验基础[6].在此基础上,我国科学团队计划与欧洲量子通信团队合作,发射多颗量子通信卫星建成全球化的广域量子通信网络.

量子信息在自由空间传输时,量子态的纠缠度、相位、保真度、偏振、极化以及量子信道的各种参数不可避免地会受到自然环境干扰的影响.因此,目前“墨子号”量子卫星通信实验仅能在夜间进行.但要建设全球量子卫星广域通信网,就必须解决量子卫星星地间的24 h全天候通信这一难题.2017年,潘建伟团队[7]首次克服了太阳光带来的噪声,实现了白天53 km以上的自由空间量子密钥分发.文献[8]研究了中尺度沙尘暴对量子卫星通信的影响.文献[9]分析了PM2.5大气污染对自由空间量子通信性能的影响.文献[10]研究了大气湍流对远距离量子通信的影响.文献[11]定量研究了灰霾粒子与水云粒子不同混合方式对量子卫星通信性能的影响.文献[12]研究了冰水混合云与量子信道衰减的关系.文献[13]研究了中纬度地区电离层偶发E层对量子卫星通信性能的影响.文献[14]研究了空间尘埃等离子体对量子卫星通信性能的影响.文献[15]研究了非球型气溶胶粒子及大气相对湿度对自由空间量子通信性能的影响.文献[16]研究了雷暴雨对星地量子链路性能的影响.

以上研究都只对环境干扰下对量子通信性能的影响进行了分析,并未提出相应的方案来解决量子通信在受雾霾、沙尘暴等自然环境干扰下的生存性问题.目前国内外关于此类方案的研究尚未展开,但对这些问题的研究,决定了自由空间量子通信系统的生存性和能否可持续发展的问题,具有十分重要的意义.因此,本文为解决广域量子卫星通信网中自由空间下全天候通信这一问题,提出了基于袋鼠纠缠跳跃模型 (kangaroo entanglement hopping model,KEHM)的量子状态自适应跳变通信策略.该通信策略能够有效提升自由空间量子通信在自然环境背景干扰下的抗干扰能力,增强量子通信系统的综合免疫力,为广域量子卫星通信网的可靠性与生存性问题提供理论依据,为自由空间量子通信的健康发展奠定理论基础.

2 环境干扰下单量子态信道随时间演化分析

根据文献[17],量子纠缠度可表示为

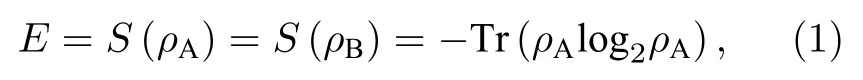
其中量子信道为子系统A; 雾霾、沙尘等自然环境背景量子噪声为子系统B.二者相互作用,约化密度矩阵为[18]

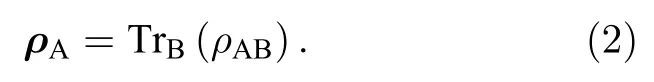
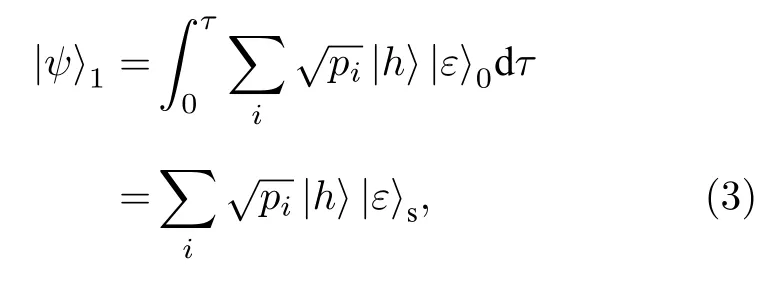
其中是 Hilbert空间中的完备基;是约化密 度矩阵的非零本征值;是量子态与自然环境背景量子噪声作用的终态;τ为量子态持续时间.在该信道下,量子信息传输会受到严重影响.

设pt为量子退极化率,在自然环境背景噪声干扰 下,量子态密度矩阵随时间最终演变为

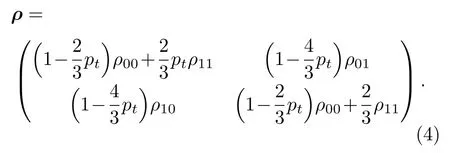
自然环境背景噪声干扰下自由空间量子信号的传输能量衰减可表示为[19]:

其中Es为量子态初态与背景量子噪声在传播一定距离后最终形成的量子态的能量;E1为量子态的初始能量;δn为量子背景噪声影响因子 ;vq为光量子传播速度.根据文献[9],令

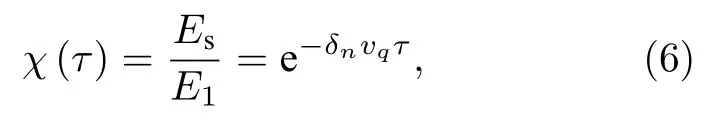
则受自然环境背景干扰时,光量子丢失概率为

量子通信幅值阻尼信道的信道容量为

其中H2(χ) 为二元香浓熵.设接收方探测器探测效率为ηdet,不受干扰条件下计数率为ℓ,量子误码率可 表示为

通过以上分析得出,在受自然环境干扰的自由空间量子通信中,采取单一的量子态作为量子信道,由于初始量子态与背景量子噪声的相互作用,通信的各性能指标都会在时间的演化下都会受到更大程度的影响.

3 基于KHEM的量子状态跳变通信策略

袋鼠是生活在澳大利亚等国的群居动物,当受到惊吓时,就会集体不约而同地远距离跳跃.多只袋鼠按照相同的模式同步跳跃,其跳跃步长、高度、频率、轨迹等参数相同.

为了增强雾霾和沙尘暴背景下自由空间量子通信系统的生存性,我们提出基于KEHM的量子状态跳变通信策略,其核心内容是袋鼠纠缠跳跃模型.用KEHM控制量子纠缠态,使得收发端的量子态按照相同的序列跳变.KEHM的内容具体如下:

1)多只袋鼠在跳跃时,起跳时间、跳跃步长、跳跃频率、跳跃高度和跳跃轨迹均相同,我们将多只袋鼠相同参数的跳跃模式,称为袋鼠纠缠跳跃;

2)设在ti时刻,甲地袋鼠 Alice (以下简称KA)和乙地袋鼠Bob (以下简称KB)开始纠缠跳跃,如图1 和图2 所示,在 0—T1时刻,KA和KB均处于状态; 在T1—T2时刻,KA和KB均处于状态在T2—T3时刻,KA和KB都处于状态不同时刻袋鼠的跳跃状态如表1所示,KA和KB起跳时间相同,跳跃频率相同;

图1 KA 的跳跃模式Fig.1.Skip mode of KA.

图2 KB 的跳跃模式Fig.2.Skip mode of KB.

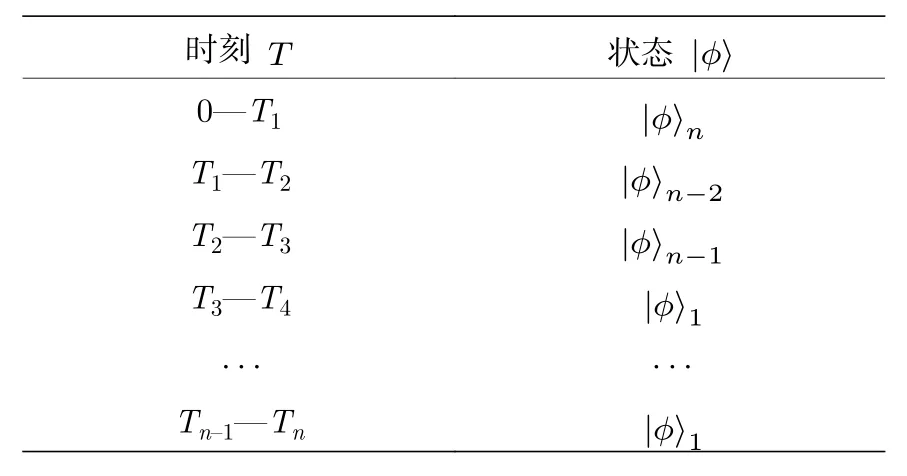
表1 不同时刻通信双方量子跳跃状态Table 1.Quantum hopping states of communication parties at different moments.

4 基于KEHM的量子状态跳变通信策略性能分析

4.1 自然环境量子背景噪声下误比特率分析

在自由空间量子通信系统中,通过量子状态跳变,能够有效地防止沙尘、雾霾等自然环境干扰.设Es为每比特信号能量,PJ为自然背景量子噪声的平均功率,量子带宽为W,则量子背景干扰功率谱密度为N0=PJ/W.宽带量子噪声对量子状态跳变通信的影响,等效为量子噪声N0,在M进制的量子通信系统中,对应的量子误比特率为

其中l=log2M.在基于KEHM的量子状态跳变通信系统中,当M=2 时,令R表示量子比特率,PJ为量子信号平均功率; 设量子态跳最小频率间隔 ∆fmin=R,KJS=PJ/PS,使量子态以频率f跳变,量子误比特率与量子态跳频率及KJS的关系如图3所示

量子误比特率Pb随着背景量子噪声平均功率与量子信号平均功率的比值KJS的增大而增大.当KJS确定时,量子误比特率随着量子态跳频率的增大而减小.KJS=5 时,随着f从 1 增大到 15,Pb从0.4524降低到0.1116.结果表明,该量子状态跳变通信策略能够通过改变量子态跳的频率从而有效降低量子系统的误比特率.

图3 量子误比特率与量子态跳频率及 K JS 的关系Fig.3.Relationship between quantum bit error rate,quantum state hopping frequency and K JS.

4.2 量子态传输性能分析

在雾霾和沙尘等背景下,基于KEHM的量子状态跳变通信过程,是一种量子级联多态通信系统.在量子态跳变的过程中,若每一种量子态传输成功率为p,相应的量子误比特率为Pb,用Xn表示第n次状态跳变后的系统输出结果,则{Xn,n1}是以S={0,1} 为状态空间的齐次马尔可夫链,其状态转移概率矩阵为

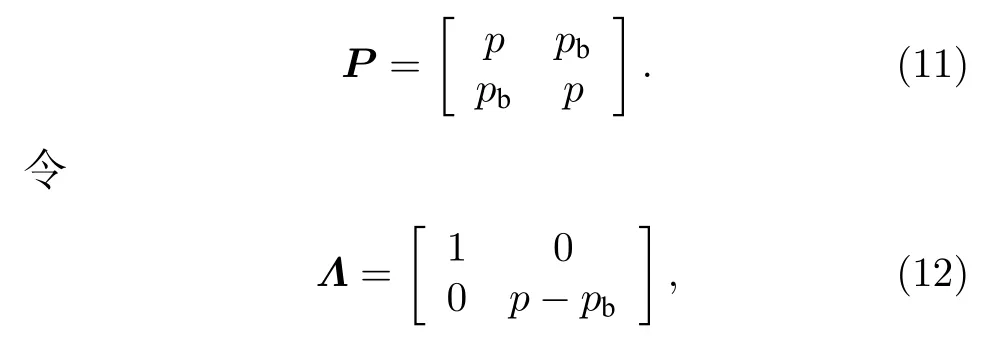
则每比特量子态的成功传输概率为

其中H为 Hardmard 算符.取p=0.95,背景量子噪声与量子信号平均功率比值为1,在不同量子状态跳变频率f下,量子比特的成功传输概率与量子比特率的关系如图4所示.

由于量子态的持续时间越长,其性能参数受环境影响越大,量子比特的成功传输概率Pr随着量子比特率R的增大而增大.对于同量子比特率,量子状态跳变频率f越大,量子比特传输成功率Pr越小,但量子比特率越大,f对传输成功率的影响越小.如图4 所示,在f=10 Hz,f=50 Hz,f=100 Hz的情况下,当R=200 qubit/s时,均有Pr>0.97.

图4 量子比特成功传输概率与量子比特率的关系Fig.4.Relationship between the probability of successful quantum bit transmission and the quantum bit rate.

在雾霾和沙尘等自然环境背景下,令µ为信号源平均量子数,自由空间量子通信系统的量子数κ服从Poisson分布.信号源发射的量子态可以表示为[20]

试验原料为太西无烟超低灰纯煤和粘结剂；试验设备主要包括磨粉机、除尘器、辊式压块机、粉碎机、整粒机、直线筛、振动给料机、炭活化一体炉等。太西无烟超低灰纯煤的工业分析与元素分析见表1。

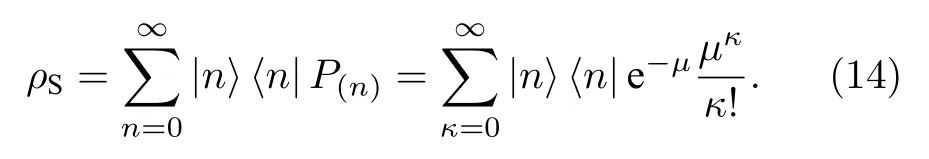
在量子状态跳变系统中,量子传输效率可等效为每比特量子态的成功传输概率.设ηB为接收端的量子接收效率,接收端的量子探测率为

则在雾霾沙尘等环境干扰下,经过量子状态跳变后,量子态的通过率可表示为

当Pr=0.95 时,量子态通过率与接收端量子接收效率及信号源平均量子数的关系如图5所示.

量子态通过率Q与接收端量子接收效率ηB成正比,且随着信号源平均量子数µ的增大,接收端量子接收效率ηB对Q的影响越小.当接收端量子接收效率ηB=0.8 时,随着信源平均量子数µ从1增加到10,量子态通过率Q由 0.3667增大到0.9986; 当信源平均量子数µ=6 时,随着接收端量子接收效率ηB从0.2增加到0.99,量子态通过率Q由 0.6262 增大到 0.9855.当µ足够大且ηB趋近于1时,量子态的通过率也趋近于1.通过合理选择量子态数目,能够有效提升量子状态跳变通信策略下系统的量子态通过率,进一步增强系统的抗干扰 能力.

图5 量子态通过率与接收端量子接收效率及信号源平均量子数的关系Fig.5.Relationship between the quantum state pass rate and the receiver's quantum reception efficiency and the average quantum number of the signal source.

5 基于KEHM的量子状态自适应跳变

5.1 量子状态跳变自适应控制策略

实时量子信道检测通过监测各个量子状态信道的各种参数从而确定该量子态信道的质量及信道接收功率的强弱,判断其是否受到干扰和能否进行正常的量子通信.本文提出基于实时量子信道状态检测的量子状态跳变自适应控制策略,其核心思想是实现从量子状态跳变的量子态集中去除被干扰严重的量子态,实现Alice和Bob间在低强度干扰的量子态上同步跳变.具体内容如下:

2) Bob通过反馈评估信息告知Alice放弃之前传输所用被判定为受干扰严重的无效量子态的信道;

3) Bob选择量子状态表中未被干扰且可使用的量子态作为代替,完成可用量子状态表的更新,并通知Alice;

5.2 量子状态跳变自适应控制平均处理时间分析

在量子状态跳变自适应控制机制中,受干扰量子态的平均处理时间Tj可表示为

其中θj为受干扰的量子态数目;Tji(θj) 是 关于θj的函数.Tj可分为 3 个部分: 受干扰量子态的检测与计算时间Ta,报告量子态参数的时间Tb与应答信息的传输时间Tc,Tj也可表示为Ta+Tb+Tc.设每个量子态出现的频率为 1 /θ,所以每个量子态受干扰检测与计算的平均时间Ta近似为

其中θ为量子态的数目;Kq为对某个量子态的观察次数.在报告量子态参数时,能容忍的最多受干扰量子态数为θ– 1,所以Tb的最大值为Tbmax=θ/f,应答信息的传输机制与量子态参数报告机制类似,有Tcmax=Tbmax.则

当只有一个量子态收到干扰时,即i=1 时,有量子态受干扰检测与计算平均时间的最小值

由于量子状态跳变的遍历性,若量子状态跳变序列中相邻两个量子态不重复,有

其中Psr为量子态被严重干扰的概率.取f=100 Hz,Kq=3,讨论量子态数目与其被严重干扰的概率与平均自适应处理时间的关系,如图6所示.

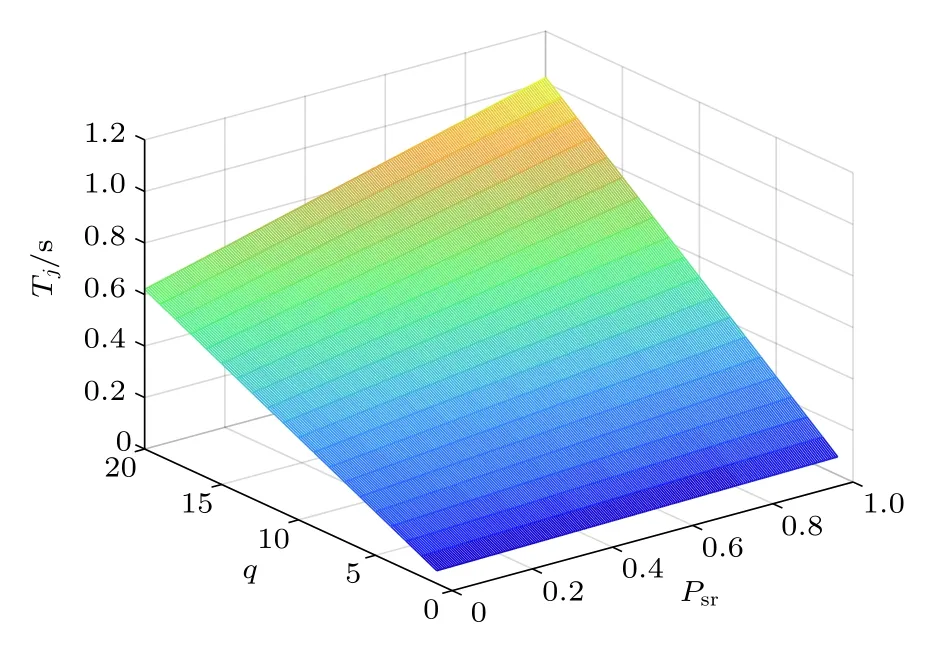
图6 量子态数目、被严重干扰的概率与平均自适应处理时间的关系Fig.6.Relationship between the number of quantum states,the probability of serious interference,and the mean adaptive processing time.

量子态跳自适应处理是一个暂态过程,量子态数目越多,被严重干扰的概率越大,暂态持续时间越长.在经过处理后,系统进入一个相对稳定的状态.

5.3 量子状态跳变自适应控制策略系统增益

根据量子状态跳变自适应处理策略,受干扰的量子态数目为θj,设成功处理的受干扰量子态数的概率为Pme,经量子态跳自适应处理,系统的误码率近似为

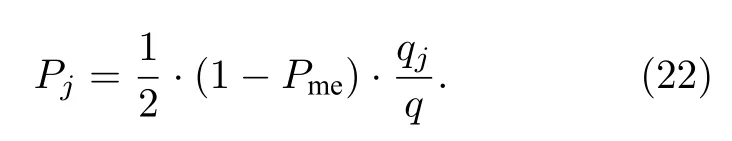
设t为量子状态跳变自适应处理持续时间,有tmax=Tj,则 (22)式可改写为

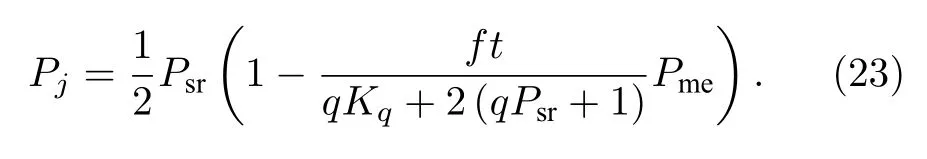
当t=tmax时,系统达到稳态.在同干扰情况下,未经量子状态跳变自适应处理的系统稳态误码率为定义量子状态跳变自适应控制策略的误码率增益Aq为

取θ=30,Psr=0.5,量子态跳自适应控制策略系统增益如图7所示.

量子状态跳变自适应控制策略系统误码率增益Aq随着成功处理受干扰量子态概率Pme的增大而增大.当Pme=0.8 时,系统增益Aq=0.699 ;Pme=0.95时,系统增益Aq=1.301.在基于 KEHM 的量子状态跳变的自适应控制机制中,通过提升系统处理受干扰量子态的能力,能进一步降低基于KEHM的量子状态跳变通信系统的误码率,使量子状态跳变系统性能得到明显改善.

图7 量子态跳自适应控制策略系统增益Fig.7.Gain of the quantum state hopping adaptive control system.

6 结 论

面向广域量子卫星通信网全天候通信问题,针对雾霾、沙尘等自然环境干扰下自由空间量子通信的性能及生存能力,根据在背景干扰下一个量子态持续时间越长,被干扰的概率越大的特性,提出了基于KEHM的量子状态自适应跳变通信策略,对该策略的可行性进行了理论研究,并对其性能进行了定量分析.仿真结果表明,在自然环境背景干扰下,采取量子状态跳变通信策略,通过改变量子状态跳变的频率及量子态数目等,能够有效降低量子通信系统的误比特率,提升量子信息传输的成功率,并且通过量子状态跳变的自适应控制机制,进一步优化了量子通信系统的抗干扰能力.该策略极大的增强了量子通信系统的综合免疫力,确保量子信息网络的安全性,为未来广域量子卫星通信网的健康发展提供了重要参考.