机械波和电磁波的多普勒效应的比较
陈伟锋
(宁波市效实中学 浙江 宁波 315012)
众所周知,多普勒效应是波源和观测者发生相对运动时,观测频率与波源频率不一致的现象.多普勒效应是波动特有的现象,机械波和电磁波(或光)均具有多普勒效应.尽管如此,它们发生多普勒效应时仍有其各自特点,差异来源于它们产生和传播机制有所不同.机械波的传播需要介质,波速是扰动在介质中传播的速度;而电磁波(或光)的传播不需要介质,光速不变原理指出,相对于观测者,光在真空中的传播速度恒为c;机械波的波源相对介质的运动一般远小于光速,光源速度若接近光速,则应考虑相对论效应.正确快速解答此类竞赛试题,要求学生们能推导机械波和光的多普勒效应公式、弄清公式的物理含义和适用条件,这样才能识别试题所涉的多普勒效应特征并直接应用公式进行求解.
1 多普勒效应公式的导出
我们分别就机械波和电磁波(或光)推导出多普勒效应公式,并加以比较.首先,明确两个概念,所谓波源频率就是波源单位时间内发出同相位信号的数目(完整波的数目);观测频率指观测者单位时间内接收到同相位信号的数目(完整波的数目).其次,波源发出波的相位或观测者接收到的波的相位随时间变化的规律相同,均满足
dφ=2πfdt
先讨论机械波的普遍多普勒效应公式,机械波的传播需要介质,设波源在介质中的速度大小为vs,观测者相对介质的速度大小vp,波速大小为u,如图1所示.
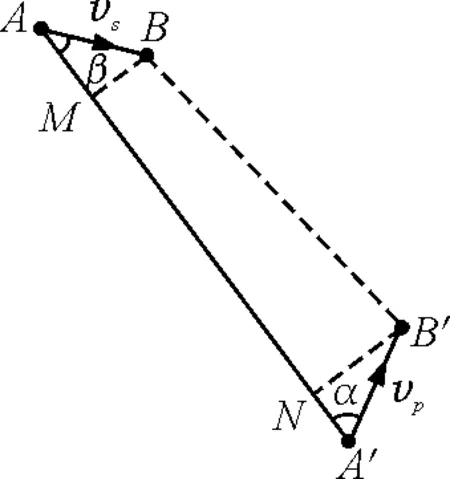
图1 机械波的普遍多普勒效应分析图

dφ=2πfdtdφ=2πf′dt′
(1)
观测者接收到这两个相位的时间差
(2)
如图1所示,过B和B′作AA′垂线垂足为M和N,由几何关系有
AA′-BB′=vsdtcosβ+vpdt′cosα
(3)
式(3)代入式(2),整理得
(u+vpcosα)dt′=(u-vscosβ)dt
(4)
式(4)代入式(1)得
(5)
式(5)为一般情况下机械波的多普勒效应公式,应用此式时应特别注意,A是波源发出某相位时所处的位置,A′是观测者接收到同一相位时所处的位置,即波源位于A和观测者位于A′并非在同一时刻.
下面推导电磁波(或光)的多普勒效应公式,电磁波(或光)与机械波有两点区别:一是电磁波(或光)的传播不需要介质,观测者所测得的真空中的光速总为c;二是当光源速度接近光速c时,还应考虑光源参考系和观测者参考系中时间的相对性,如图2所示.

图2 观测者参考系中的电磁波多普勒效应分析图
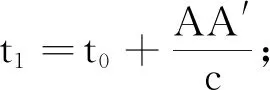
dφ=2πfdTdφ=2πf′dT′
(6)
其中,dT为光源参考系中发出两光信号的时间,是固有时,由于时间膨胀效应,它与观测者所测得的发出两光信号的运动时dt之间应满足
(7)
观测者接收两光信号的时间间隔
(8)
由几何关系
AA′-BA′=vdtcosα
(9)
联立式(6)~(9)得
(10)


(1)若光源速度v≪c,则
取一级近似得
(11)
(2)若α=0或α=π,则
(12)
此时光源向着或背离观测者运动,称为纵向多普勒效应.

(13)
此时光源速度与两者连线垂直,称为横向多普勒效应,是光特有的现象.
2 竞赛试题解析
2.1 机械波的多普勒效应
【例1】(第22届全国复赛试题)两辆汽车A与B,在t=0时从十字路口O处分别以速度vA和vB沿水平的、相互正交的公路匀速前进,如图3所示.汽车A持续地以固定的频率ν0鸣笛,求在任意时刻t汽车B的司机所检测到的笛声频率.已知声速为u,且当然有u>vA,vB.
图4给出了在λT=5,Cwf=1,ηc=ηT=0.85,D1=D2=0.96时,双重最大功率时的总压比与循环温比的关系.由图可知,双重最大功率时的总压比与循环温比基本成正比关系.
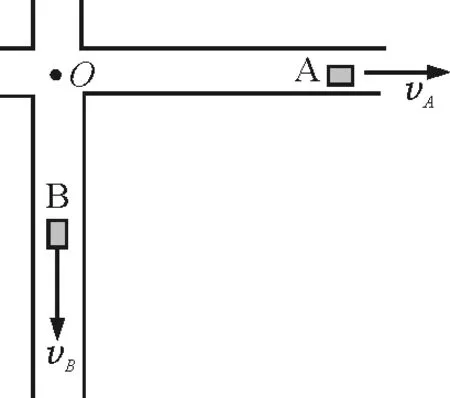
图3 例1题图
分析与解:本题为机械波的多普勒效应,而且波源和观测者相对介质的速度与两者连线不在一条直线上,可直接应用式(5),代入相关数据计算,应用此式要注意两点,一是由于车速相对于声速并不能忽略,波源和观测者的连线并不是同一时刻的位置连线;二是本题中速度与连线的夹角均为钝角,应取负值,即两车速度在连线上的分速度与两者相背离.
题中,汽车B上司机为观测者,汽车A为波源,如图4所示.
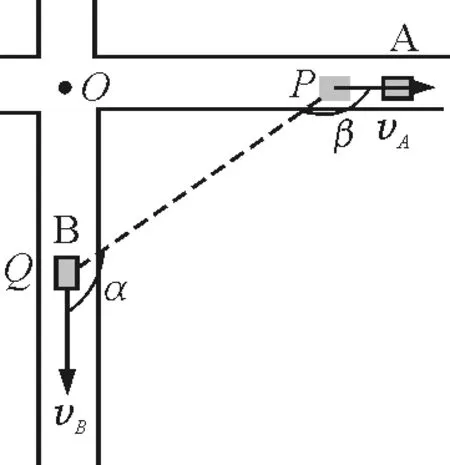
图4 以B中的司机为观测者,A为波源的图示
设在时刻t汽车B位于Q处正接收到相位φ,此相位是汽车A在更早的时刻t-Δt位于P处发出的,而声音从P传到Q处的时间为Δt,有
OQ=vBtOP=vA(t-Δt)PQ=uΔt
(14)
由几何关系
PQ2=OP2+OQ2
(15)
由式(14)、(15)解得
(16)
2.2 电磁波(或光)的多普勒效应
【例2】(第32届全国复赛试题)如图5所示,飞机在距水平地面(xz平面)等高的航线KA(沿x正方向)上,以大小为v(v远小于真空中的光速c)的速度匀速飞行;机载雷达天线持续向航线正右侧地面上的被测固定目标P点(其x坐标为xP)发射扇形无线电波束(扇形的角平分线与航线垂直),波束平面与水平地面交于线段BC(BC随着飞机移动,且在测量时应覆盖被测目标P点),取K点在地面的正投影O为坐标原点.已知BC与航线KA的距离为R0.天线发出的无线电波束是周期性的等幅高频脉冲余弦波,其频率为f0.

图5 例2题图
(1)已知机载雷达天线经过A点(其x坐标为xA)及此后朝P点相继发出无线电波信号,由P反射后又被机载雷达天线接收到,求接收到的回波信号的频率与发出信号的频率之差(频移).
(2)已知BC长度为Ls,讨论上述频移分别为正、零或负的条件,并求出最大的正、负频移.

分析与解:本题为电磁波的多普勒效应,由于飞机速度v远小于真空中的光速c,故不必考虑相对论效应,用式(11)即可;因飞机与地面P点距离相对电磁波速度c极短,飞机发出信号到接收到回波信号的时间内,飞机的位移可以忽略不计.
(1)如图6所示,在KA和BC所在的平面内,连A和P并过P点做KA垂线交KA于Q.

图6 (1)问分析图
由几何关系得
(17)
故P接收到的频率
(18)
式(17)代入式(18)得
(19)
由于v≪c,故不必考虑从发出信号到接收到回波信号过程中飞机的位移.
同理,飞机接收到的信号频率
将式(19)代入得
取一级近似得
(20)
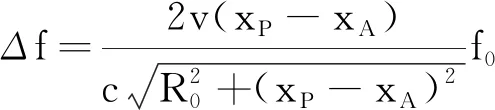
(21)
(2)分析图如图7所示.

图7 (2)问分析图
由式(5)可知,当xP>xA时频移为正,当xP=xA时频移为零,当xP (22) (3)结合式(22)得带宽 当R0≫Ls时,有 故 从以上两题的解析我们不难发现,对机械波,波源速度一般都远小于光速,与波速相差不大,不必考虑相对论效应,但应考虑波在传播过程中波源或观测者相对介质的位移.对于电磁波或光,需要明确波源速度与光速的大小关系,确定是否要考虑相对论效应.只要明确公式的适用条件和物理含义,对此类试题不必从最基本的相位和时间关系出发去解答,从而可以减少答题篇幅,节省解答时间.

