基于蚁群算法的地铁车站行人拥挤等级划分方法

周继彪，赵鹏飞，董 升，张水潮

(1.宁波工程学院建筑与交通工程学院，宁波浙江315211；2.同济大学交通运输工程学院，上海201804；3.北京工业大学建筑工程学院，北京100124)

0 引言

随着中国城市轨道交通客流量迅猛增长，加之客流时空的高度积聚性，设施运量、运力以及服务水平的短板亟待弥补。同时，客运总量、日均客运量、平均客运强度持续攀升以及最小发车时间间隔相对缩短等对网络化运营条件下地铁车站运营的安全管理提出了更高要求。2018年中国城市轨道交通年客运总量超过210.7 亿人次，较2017年增长25.9亿人次，增长14%。全国城市轨道交通高峰小时最小发车间隔平均为265 s。进入120 s 及以内的线路共有10 条，其中以上海地铁9号线115 s最短，广州地铁3号线118 s次之[1]。高峰时段乘客乘车困难问题频发，类似的情况也发生在欧洲的巴黎、伦敦和其他大城市[2]。公共交通的服务质量尤其是拥挤问题已成为全球共同面临的、亟须解决的问题。

作为典型的城市轨道交通系统之一，地铁在满足城市居民出行需求中发挥着重要作用，其服务水平直接受到客流拥挤程度的影响。目前地铁车站客流拥挤程度以客流拥挤强度为依据。客流拥挤强度分级方法主要分为意向(Stated Preference, SP)调查法、立席密度法、服务水平法、云模型法四类。基于SP 调查法，文献[3]以爱尔兰都柏林市市民为研究对象，量化分析不同影响因素对市民通勤压力的影响，发现通勤压力与被试者的通勤特征高度相关，减少公共汽车和火车内的拥挤程度比在可靠性方面的改善更有益处；文献[4]研究了印度孟买火车的行驶时间对其拥挤程度水平的影响，发现列车行驶的当量感知距离随拥挤程度增加而增加；文献[5]对乘客站立和就座两类情景进行测试，结果表明乘车负效用与乘客是否有座位密切相关，与乘客站立密度关系不大；文献[6]建议评估拥挤程度时应将短距离和长距离旅客分开考虑。基于立席密度法，文献[4]提出的拥挤程度水平指单位面积上站立行人的密度大小；文献[7]认为虽然个体之间的主观意见不一致，但是拥挤效应会产生负效用；文献[8]量化了乘客对拥挤程度的感受，其立席密度由车厢内载客数量除以立席所占面积(扣除座席后的面积)得到。国内外在立席密度法的划分标准制定方面存在差异，国外将立席密度分为两类：1)舒适度标准，其立席密度为3 人·m-2；2)拥挤度标准，其立席密度为6 人·m-2。中国存在三种立席密度标准：1)《地铁设计规范》(GB 50157—2013)[9]规定车辆立席按6 人·m-2、超员按9 人·m-2考虑；2)《地铁车辆通用技术条件》(GB/T 7928—2003)[10]规定车辆立席按6 人·m-2、超员按8 人·m-2考虑；3)《城市轨道交通工程项目建设标准》(建标104—2008)[11]规定车辆立席按5人·m-2、超员按8人·m-2考虑。此外，基于服务水平法，文献[12]对香港轻轨站台的拥挤度进行评估，并结合已有的服务水平等级划分标准[13]，将站台的服务水平划分为五类，与之对应的拥挤度也被划分为五级(1～5级)；文献[14]对北京市轨道交通车站内通道的服务水平进行调查，提出适合北京市轨道交通通道服务水平的划分标准。基于云模型法，文献[15]定义了拥挤度，并根据拥挤度给出枢纽内行人拥挤状态的定性描述，结合云模型，给出了拥挤度判别的具体实现过程；文献[16]针对地铁换乘枢纽拥挤状态划分中的模糊性和随机性，提出一种基于云模型的地铁换乘枢纽行人拥挤度辨识方法。

综上，已有研究在城市轨道交通客流拥挤强度量化方法上取得了大量成果，其研究对象主要是基础设施，如地铁车站、综合客运枢纽站等。当前的研究成果分别基于不同的研究方法提出了各自的指数分类标准和划分依据，由于受数据采集能力和数据精度的限制，已有研究中大多采用单一的K-means聚类分析、综合加权等多种方法对不同定义的交通指数进行分级。随着地铁车站自动售检票系统(Automatic Fare Collection System,AFC)等设备的普及以及网络传输效率的提升，对移动设备回传的大数据进行深度挖掘也将成为一种趋势，基于AFC数据的客流拥挤分级将得到良好的实践应用。鉴于此，本文提出一种基于蚁群聚类(Ant Colony Optimization,ACO)的优化算法，其思想是将客流拥挤状态的等级划分问题转化为拥挤度的聚类问题来解决，基于城市轨道交通客流拥挤特征大数据样本值进行聚类分析，从而避免具体分级标准的限制和主观因素的影响。

1 地铁车站客流分布特征分析

客流特征对地铁车站总体规模、内部设施规模和布局设计、轨道交通制式选取、车辆调度等起着决定性的作用。由于进站客流、出站客流以及进出站客流在行人服务设施占用、客流来源以及活动目的上具有差异，本文以陕西省西安市2013年3 月19 日全日客流数据为基础数据，对乘客进站、出站和进出站的客流时空特征进行分析。

1）进站客流。

进站客流一般要经过购票、安检等服务过程通往站台候车，进站客流量随时间的分布如图1a 所示。从全日客运总量的分布分析，其变化呈现明显的M形分布。早高峰集中于7：00—8：00，17 个车站的平均高峰小时系数达9.9%，龙首原站高峰小时系数最高，达 17.2%；晚高峰集中于18：00—19：00，车站的平均高峰小时系数达11.1%，南稍门站高峰小时系数最高，达14.8%。

2）出站客流。

出站客流一般通过站台、楼梯等服务设施直接出站，相比进站客流程序较为简单，出站客流随时间的变化规律如图1b 所示。与进站客流类似，全日出站客流依然呈现出明显的M 形客流分布。早高峰集中于8：00—9：00，车站平均高峰小时系数 达12.2%，永宁门站高峰小时系数最高，达19.8%；晚高峰集中于 18：00—19：00，车站平均高峰小时系数达11.4%，龙首原站高峰小时系数最高，达17.1%。

3）进出站客流。

由于进出站客流同时占用枢纽内部行人设施，且在通道、站台等设施容易出现交织或冲突现象，极易出现拥挤。因此，进出站客流量是分析车站总体运行情况的重要指标。进出站客流随时间的分布规律如图1c所示，可以看出，进出站客流量在一日中仍为M 形客流分布。早高峰集中于 8：00—9：00，车站平均高峰小时系数达11.1%，永宁门站高峰小时系数最高，达14.5%；晚高峰集中于17：00—18：00，车站平均高峰小时系数达11.3%，南稍门站高峰小时系数最高，达12.8%。

2 客流拥挤指数分级建模

2.1 拥挤指数分级方法

城市轨道交通客流拥挤指数旨在表征地铁车站内部客流运行状态。以地铁车站内部客流时空分布特征为依据，综合考虑客流拥挤强度、客流拥挤持续时间以及客流拥挤影响范围3 个方面对行人拥挤状态进行等级划分。

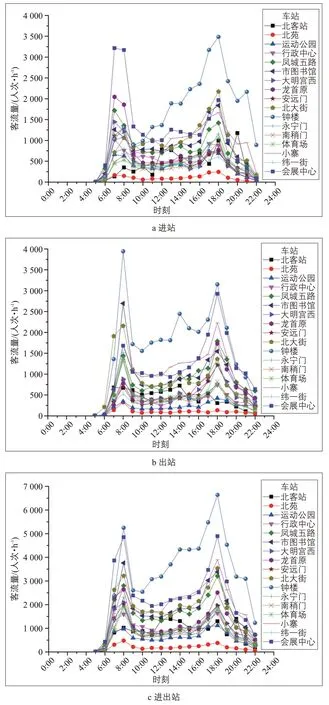
图1 客流分布特征Fig.1 Characteristics of passenger flow distribution

1）客流拥挤强度。

客流拥挤强度(以下简称“拥挤强度”)以客流在单位时间内的平均密度来表征：

2）客流拥挤持续时间。

客流拥挤持续时间(以下简称“拥挤持续时间”)是影响乘客拥挤感受的重要因素之一。通过统计不同行人密度的累积频率分布情况，将其进行函数拟合，得到行人密度的累积频率分布曲线，再将其求导并取倒数后得到在不同行人密度处的变化速率，以此来表征客流的拥挤持续时间。根据AFC数据统计，行人密度累计分布曲线为对数函数

式中：y为行人密度为x时的累积频率；x为地铁车站内的行人平均密度/(人·m-2)；a，b分别为拟合函数的常量。将公式(2)求导并取倒数得到

式中：dx/dy体现了行人密度累积频率的变化快慢，其值越大则行人密度变化越快，拥挤影响越小，反之，行人密度变化越慢，拥挤影响越大；x/a为行人平均密度为x时的持续时间。

3）客流拥挤影响范围。

客流拥挤影响范围(以下简称“拥挤影响范围”)为轨道交通车站内部所有行人可利用设施的面积。

4）客流拥挤指数。

由于拥挤强度指标中已经体现了拥挤影响范围指标，为有效展示这三方面的累积效应，仅需将拥挤强度和拥挤持续时间相乘，即可得到客流拥挤指数PCI(Passenger Crowed Index)，即

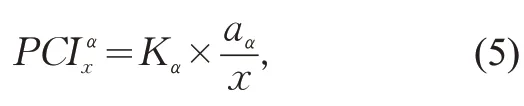
2.2 分级求解算法

地铁车站拥挤等级的划分与聚类思想一致，都是将同一属性的相同或近似值的样本数据进行归纳的过程[17-18]。将地铁车站内的拥挤等级划分问题转化为聚类问题来解决，其结果既能揭示不同等级内部的隐含关系，还有利于进行地铁车站内部运行质量研判。针对目前行人拥挤度量化缺乏分级标准等问题，提出基于改进蚁群聚类的拥挤分级算法，该算法对地铁内部拥挤指数进行自动聚类，可实现层次性分级。

基于计算效率高、鲁棒性强的优点，选取基于蚁群觅食原理的蚁群聚类算法。主要分为搜索食物和搬运食物两个阶段，每只蚂蚁在移动的过程中都会在其经过的路径上释放一定的信息素，蚂蚁能够感知信息素的存在并判断其浓度。路径上经过的蚂蚁越多，其信息素的浓度越强，但同时路径上信息素也会随着时间的推移而挥发。蚂蚁倾向于向信息素强度高的方向移动，某一路径上爬过的蚂蚁越多，后者选择该路径的概率越大，整个蚁群的行为就表现出信息的通信。在Kmeans 算法中，引入蚁群的转移概率，得到蚁群聚类分析算法。

2.2.1 基本原理

将拥挤度数据点视为具备若干属性的蚂蚁，而将拥挤度分级中心视为食物源，在明确分级数量M的基础上，将具有n个属性的N个待分析的拥挤度定义为

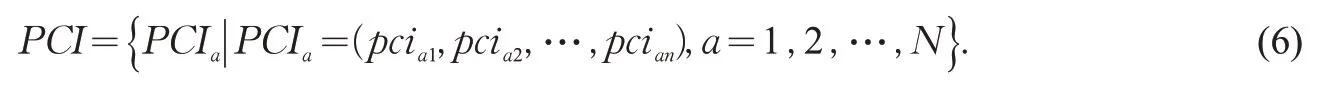
不同拥挤度之间的偏离误差用欧几里得距离来度量，距离越小，偏离误差就越小。将拥挤度pciai分配给第j个聚类中心(j=1，2，…，J) ，蚂蚁就在拥挤度样本pciai到聚类中心Cj的路径 (pciai，pciaj) 上留下信息素τij(c) ，用表示拥挤度PCIi和PCIj属性空间的加权欧氏距离

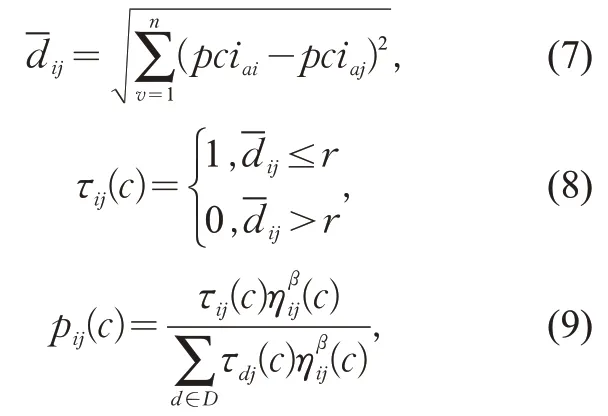
式中：r为聚类半径，无量纲数值；pij(c)为蚂蚁选择路径(pciai，pciaj)的概率；为g次迭代中拥挤度i分配到第j个聚类中心启发信息的数值，采用两者之间距离的倒数来定义；β为期望启发因子，表征蚂蚁在运动过程中启发信息的受重视程度；为 蚂 蚁PCIj可供选择的路径。当pij(c)≥P0时，将PCIi与PCIj合并，P0为基础概率，即拥挤度PCIi分配至前j个聚类中心适配度的累加值。当移动所有蚂蚁之后，每个类中所包含的拥挤度将会发生变化，则各个类的聚类中心点需要重新计算，同一类内部的偏离误差也需计算更新。用Cj表示归并到Xi领域的所有聚类集，新的聚类中心与偏离误差E计算如下：

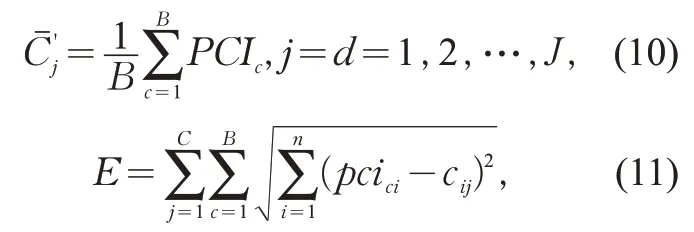
式中：B为新聚类中心的所有元素数量；C为迭代后新聚类中心的数量；J为Cj的元素数量；cij为的第i个分量。

同时，给定最大迭代次数，只要满足以下任一条件则聚类结束并给出分析结果：1)所有类的偏离误差总量小于参数ε；2)迭代次数达到给定的迭代次数最大值。否则，应重新进行计算，直到满足条件终止。

2.2.2 算法步骤

对改进的蚁群聚类算法进行编程，求解拥挤度分级临界值，过程如下：

第1 步：初始化参数，确定拥挤度的样本量N，最大迭代次数G，样本量属性数量n及初始全局信息素矩阵；

第2 步：根据全局信息素矩阵开始进行迭代，确定蚂蚁行走路径并进行标记；

第3 步：根据路径标识得到当前的聚类中心，并计算所有样本到对应聚类中心的偏离误差总量E，得到最小偏离误差E-min；

第4 步：产生随机数，并由此对当前最优路径进行改变，并计算新路径下所有样本到对应聚类中心的偏离误差总量E'；

第5 步：判断E'是否小于E-min ，若是，则当前路径为最优路径，直接输出结果，算法结束；若不是，则进行下一步；

第6 步：判断当前的迭代次数是否达到最大值G，若是则直接输出结果，算法结束；否则返回第2步，进行下一轮迭代。

2.2.3 算法流程

为克服传统的蚁群聚类算法得到满意解效率低的缺点，对传统的蚁群聚类算法迭代过程中的路径更新规则进行改进，改进的算法基本流程如图2所示。

3 实例验证

3.1 数据来源

基于西安市轨道交通AFC系统提供的历史客票数据进行分析。西安地铁各运营线路的AFC 系统使用非接触式IC 卡作为车票媒介，其客流统计主要是依据进出站闸机的刷卡和投票数据来统计，每位乘客进出站时的刷卡和单程票都会产生一个交易文件，上传到车站服务器，然后传送到清算管理中心，最后由AFC工作人员针对这些交易文件统计出各运营线路的实时客流。

AFC系统详细记录了每一位持卡乘客的出行信息，包括卡号、卡类型、乘车日期、进站编号、进站线路、进站时间、出站时间、出站线路、出站编号、总计出行时间等，通过对AFC数据的分析和整理，可以获取各运营线路准确、连续的客流大数据。

选取西安地铁2013年3月19日两条线(1号线和2号线)全日所有车站分时段(5：00—22：00)、分车站进出站客流数据进行分析，包括北客站、北苑、运动公园、行政中心、凤城五路、市图书馆、大明宫西、龙首原、安远门、北大街、钟楼、永宁门、南稍门、体育场、小寨、纬一街和会展中心共计17 个车站。选取进出客流量较高的6 个车站的行人设施可利用面积进行实地调查，并结合西安市地下铁道有限责任公司提供的原始数据，推算得到车站行人设施面积与车站建筑面积的比值均接近0.8(见表1)，因此取有效折算系数为0.8，可根据车站建筑面积推算行人设施有效利用面积。

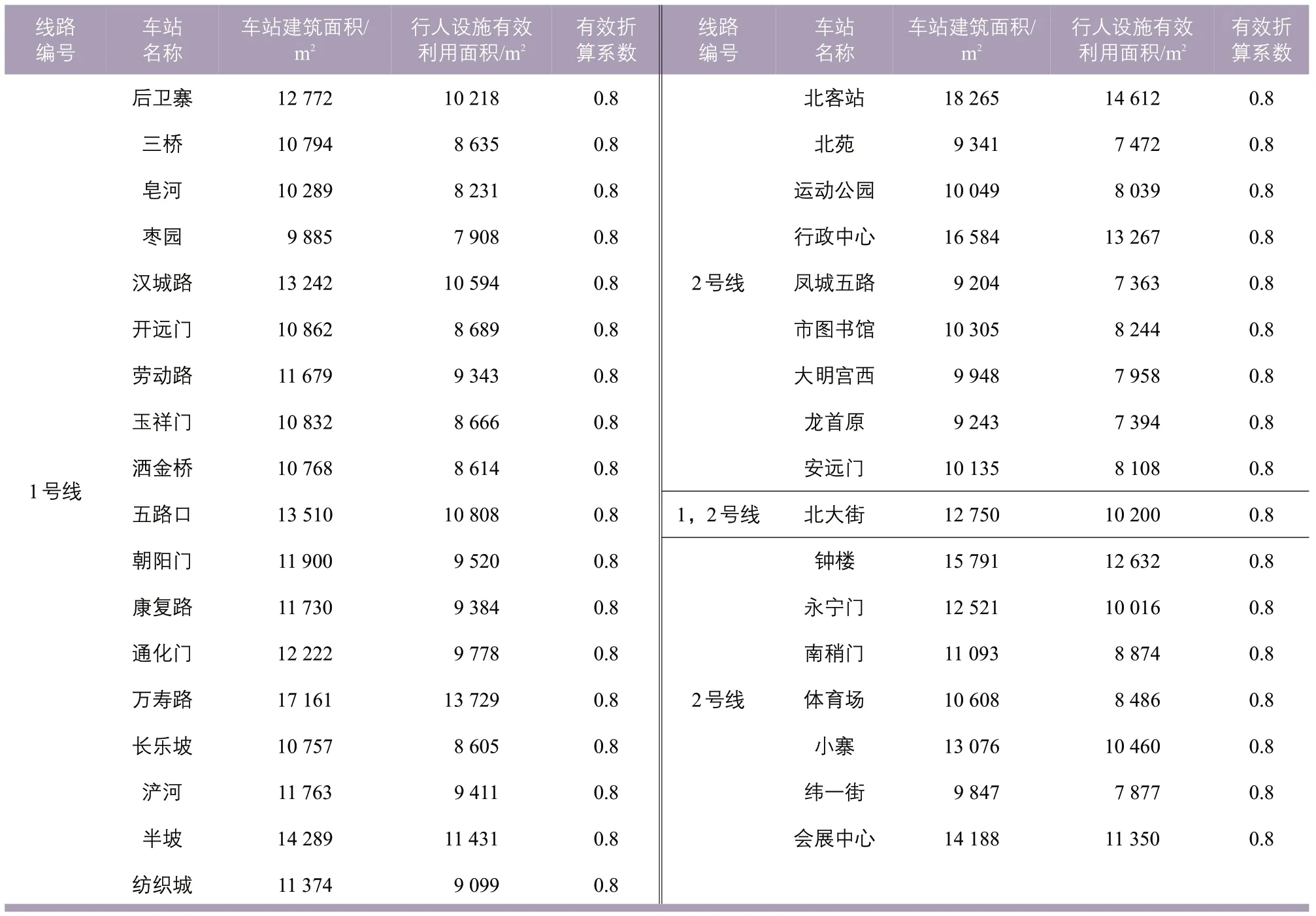
表1 车站建筑面积及行人设施面积统计Tab.1 Statistics on station floor area and pedestrian facilities area

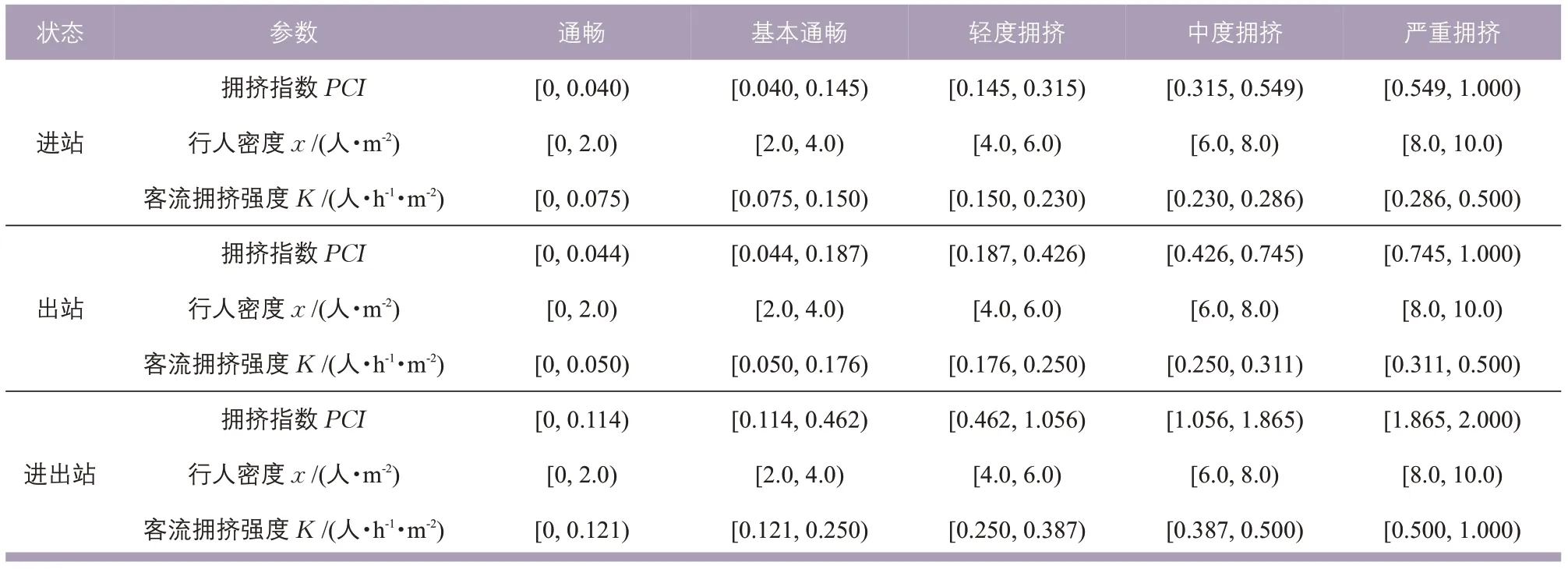
表2 客流拥挤状态划分结果Tab.2 Classification of pedestrian congestion state

3.2 拥挤分级

针对行人在地铁车站内部的拥挤强度、拥挤持续时间以及拥挤影响范围三方面进行拥挤指数计算，利用改进的蚁群聚类算法，分别得到进站、出站以及进出站三种状态下的聚类结果。

根据图3 可知，进站、出站以及进出站客流密度累积频率分布曲线分别为：

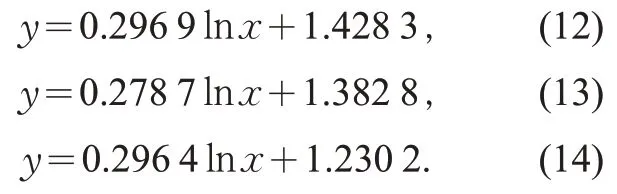
这三个曲线均属于对数函数，表明客流量随着客流密度的增加而降低。同时，可得进站、出站以及进出站三种状态下行人密度为x时的行人密度变化速率

通过比较公式(15)～(17)发现，进站、出站以及进出站三种状态下的行人密度变化速率差别较小，尤其是进站与进出站更为接近，这与实际情况相符。通过改进蚁群聚类算法，设置信息素蒸发率为0.1，蚂蚁数量为50，行人密度以及不同时段的聚类结果如图4所示。

图4 中的颜色综合反映地铁车站内行人的拥挤状态，左侧纵轴为行人密度值，右侧纵轴为不同等级的拥挤指数。根据图4 的聚类结果，判定客流拥挤状态为5 个等级，分别为通畅、基本通畅、轻度拥挤、中度拥挤和严重拥挤，反映地铁车站内部客流的运行状态，数值越高表明地铁车站内行人拥挤状态越严重，结果如表2所示。

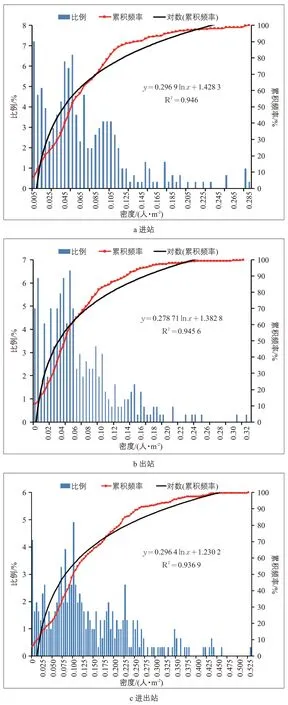
图3 客流密度累积频率分布Fig.3 Cumulative frequency distribution of passenger density

图4 不同状态下客流拥挤指数聚类结果Fig.4 Clustering results of passenger congestion in different states

1） 针对进站、出站和进出站三种状态，地铁车站的行人拥挤变化呈现较明显的时空差异特征，17个车站内的行人拥挤状态均在列车运行周期内上下波动，全日地铁客流在时空特征上呈现出明显的M形分布，早高峰集中于8：00—9：00，平峰集中于10：00—16：00，晚高峰集中于18：00—19：00。其原因为该时段内地铁客流主要为通勤客流。

2）三种状态下，行人密度累积频率分布曲线符合对数函数，表明客流量随着客流密度的增加而降低。当考虑拥挤强度、拥挤持续时间和拥挤影响范围时，客流拥挤指数的等级划分具有非线性特征。客流拥挤状态对应的通畅、基本通畅、轻度拥挤、中度拥挤和严重拥挤的阈值边界，进站时为0.040，0.145，0.315，0.549，1.000； 出 站 时 为0.044，0.187，0.426，0.745，1.000；进 出站时为0.114，0.462，1.056，1.865，2.000。

3）三种状态下，17 个车站的拥挤指数呈现周期性变化，且各车站之间的拥挤状态变化较大。这主要与发车时间间隔有关，地铁1 号线和2 号线的发车时间间隔为5 min 30 s，17 个车站的行人拥挤状态变化周期约为5 min 30 s，其行人拥挤等级变化周期与列车到站时间基本一致，进一步验证了蚁群聚类优化算法的有效性。

4 结语

如何提升城市轨道交通线网的运营水平，科学表征网络化运营条件下轨道交通大客流的拥挤程度级别，进一步提升轨道交通科学应对突发大客流的快速决策和疏散能力，是轨道交通管理部门面临的严峻挑战。本文基于轨道交通AFC历史数据及车站行人设施有效利用面积调查数据，求解得到轨道交通车站内部拥挤强度，综合考虑拥挤强度、拥挤持续时间以及拥挤影响范围三个方面，得到客流拥挤指数。将客流拥挤指数进行聚类分级，结果与实际客流的变化具有一致性，能较好地反映客流的拥挤状态以及乘客对拥挤的感知和承受程度。利用该分级结果，有助于解决客流进出站引导以及枢纽设计瓶颈识别等问题。利用蚁群聚类算法进行聚类，有效避免了等级划分标准缺失的弊端。通过调节信息素的蒸发率和蚂蚁数量得到了良好的聚类结果，在客流拥挤指数的分级中，避免了等间距值的划分弊端，体现了拥挤强度、持续时间以及影响范围对拥挤状态的影响，证明了改进蚁群聚类算法的可行性和实用性。由于目前仅利用西安市地铁车站一日的AFC刷卡数据，样本时间跨度和样本量有限，下一步将考虑扩充和更新数据量，基于大数据视角分析蚁群聚类算法的精度和效率。

致谢：

Acknowledgement：

感谢西安市地下铁道有限责任公司对本文所用数据的支持。文中原始数据仅用于科学研究，无任何商业用途。