高举架立式圆筒型储液容器组合减震理论分析与数值仿真分析
(1.大连万科有限公司,辽宁大连 116650;2.大连海事大学 交通运输工程学院,辽宁大连 116026;3.大连理工大学 建设工程学部,辽宁大连 116023)
0 引言
随着石油化工、建筑工业、海洋平台等行业的发展,高举架储液容器作为关键设备,一旦遭遇地震而损坏,将直接关系到生命财产安全。从已知的高举架储液容器的地震响应可知,引发高举架储液容器破坏的因素可分为储液晃动、动液压力增加、支撑体系与储液容器的锚固连接破坏、支撑体系本身的破坏、基础锚固连接件拉断等。为减轻地震对高举架立式圆筒型储液容器造成的破坏,学者们进行大量研究,研究方向主要是通过在支承底部或顶部附加隔震层来实现减震目的。1990年,Chalhoub等[1]分析了基础隔震措施对储罐地震响应的影响,结果表明,相对于抗震结构,基础隔震措施能明显减小储液动态压力,但储液晃动会略有放大;1994年,Liang等[2]对高举架储罐采用隔震措施,进行了单一地震动输入有限元数值仿真模拟,得出采用隔震设备后能有效减小储液动液压力对罐壁的作用;1993年,Bleiman等[3]提出将隔震作为一种有效的减震措施引入到高举架储罐抗震中;1999年,Shenton等[4]通过在支承底部植入隔震层,对高举架储液容器实行地震动数值分析,得出在支承底部植入隔震层是行之有效的减震方式,但简化分析模型中并未研究弹性罐壁翘曲作用;2003年,Shrimali等[5]对高举架隔震储罐进行了地震作用研究,结果表明,隔震能够降低地震作用;王振等[6-8]利用地上储罐简化力学模型附加支撑体系,对高举架储罐采用基础隔震措施,开展了地震作用数值研究,从不同隔震基频、不同储罐容积、不同场地条件等几个方面入手,论证了隔震技术的可行性;2011年,Curadelli[9]对球形储罐附加消能减震支撑,采用有限元数值仿真技术进行了地震响应数值分析,结果表明,附加减震耗能装置后,地震响应明显降低;2016年,吕远等[10]进行高举架立式圆筒型储液容器基础隔震有限元数值仿真分析,并研究不同隔震层参数、不同储液高度以及不同地震动刚输入时,基础隔震的减震率,为基础隔震的设计提供支持。
但当遭遇强震时,单一减震方式可能无法满足抗震设防要求,由此,本文基于现有的隔震方式,通过在支承结构上附加黏滞阻尼器,提出两种组合减震方式,即基础隔震与黏滞阻尼器组合减震、柱顶隔震与黏滞阻尼器组合减震,分别简称为组合减震A、组合减震B;并以某一工程实例为例,从理论研究及有限元数值仿真分析两个方面进行地震动响应对比分析。
1 理论分析
1.1 简化力学模型及运动控制方程
高举架立式圆筒型储液容器具有一定的高度,支承结构通常为多层钢筋混凝土框架结构和钢结构。本文主要以多层钢筋混凝土框架结构支承为研究对象,将支承结构每一层集中为一个质量点,取每层框架上下柱反弯点为集中质量分割点,如图1(a)所示。而对于上部储罐,可将其视为立式储罐,将罐内液体质量简化为对流质量mc和刚性质量mr;对流质量由等效弹簧刚度kc及阻尼常数cc与罐壁相连,刚性质量与罐壁刚性连接。以某一6层高举架立式储液容器为例,抗震简化力学模型如图1(b)所示。在支承结构的顶部和底部分别装置隔震层,同时在每一层框架上植入多个斜撑式黏滞阻尼器,不考虑阻尼器刚度影响,可得出组合减震A及组合减震B的简化力学模型,如图1(c),(d)所示。
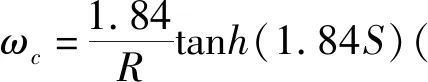

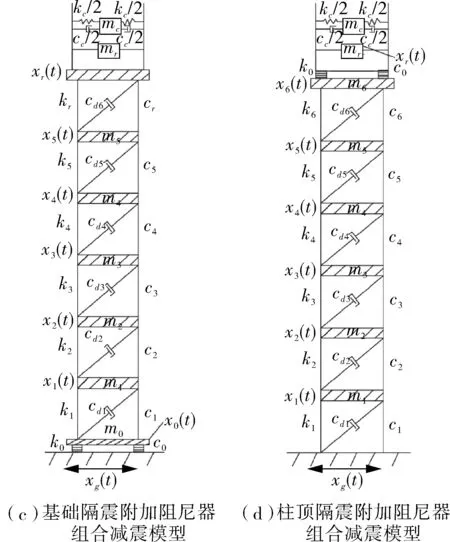
图1 简化力学模型
根据结构动力学中的层剪切恢复力模型,得到运动控制方程为:
(1)

[M],[Meq]——质量矩阵;
[K]——刚度矩阵;
[C]——阻尼矩阵,通过Rayleigh阻尼模型得出,[C]=α[M]+β[K];
Fd——黏滞阻尼器提供阻尼力。
(1)对于基础隔震与阻尼器组合减震模型,有以下公式。
罐底剪力、基底剪力、倾覆弯矩及晃动波高方程式分别如下:
Qg=mrar+mcac
(2)
Q=m0a0+m1a1+…+m5a5+mrar+mcac
(3)
MQ=m0a0h0+m2a2h2+…+m5a5h5+mrar
×(h+hr)+mcac(h+hc)
(4)
hv=0.837Rac/g
(5)
式中a1,…,a5,ar,ac——绝对加速度,为式(1)中所求出的相对加速度逐层累加所得;
h1,h2,…,h5——支承各层距地面高度;
h——支承总高度;
hr,hc——储液刚性质量和对流质量的等效高度。
(2)对于柱顶隔震与阻尼器组合减震模型,有以下公式。
罐底剪力及晃动波高表达式同式(2),(5),基底剪力、倾覆弯矩方程式分别如下:
Q=m1a1+m2a2+…+m6a6+mrar+mcac
(6)
MQ=m1a1h1+m2a2h2+…+m6a6h6+mrar
×(h+hr)+mcac(h+hc)
(7)
式(6),(7)中各参数意义与式(2)~(5)一致。
1.2 算例分析
参照文献[12]中高举架立式圆筒型储液容器工程实例进行地震动响应分析。该高举架立式圆筒型储液容器实际工程情况为6根支柱呈正六边形分布,支架总高H=32.5 m,分6层,支柱与圈梁尺寸如表1所示。

表1 算例参数
塔身顶部半径2.4 m,底部半径4.025 m,倾斜度为1/20。平台板厚度300 mm。梁、柱、板均为混凝土,杨氏模量E=2.6×1010N/m2,泊松比υ=0.16,密度ρ=2 400 kg/m3。钢制拱顶圆筒型储罐半径2.4 m,高3 m,底板和罐壁厚度均为10 mm,拱顶厚度6 mm,υ=0.3,E=2.06×1011N/m2,屈服强度ReL=490 N/mm2,剪切模量G=39.73 N/mm2。罐内液面高度2.2 m,ρ=103kg/m3。
本文隔震层隔震周期取2 s,阻尼比取0.1,根据式(5),(6)可算得隔震层的等效刚度和等效阻尼分别为:253 716 N/m,16 160 N·s/m。根据翁大根等[13]提出的附加黏滞阻尼器减震结构使用设计方法,取阻尼器速度指数0.5,可计算出所需附加阻尼器参数如表2所示。

表2 阻尼器参数
(a)金门公园地震波

(b)北京饭店地震波

(c)El Centro地震波

(d)Pasadena地震波
选取金门公园、北京饭店、El Centro和Pasadena四种不同类型的地震波为地震动输入,加速度峰值均为0.2g,如图2所示。非线性运动方程基于Newmark-β数值分析方法,采用牛顿迭代求解。以晃动波高、罐底剪力、基地剪力、倾覆弯矩、层间位移角为控制目标,进行地震动响应对比分析,计算结果如表3~6所示。

表3 金门公园地震动响应峰值
注:层间位移角=相邻楼层间上下楼层的相对位移/层高

表4 北京饭店地震动响应峰值

表5 El Centro地震动响应峰值

表6 Pasadena地震动响应峰值
从表3~6可以看出,不同地震动输入时,两种组合减震方式的减震效果各不相同。对于El Centro,Pasadena两种地震动输入,两种组合减震措施均有较好的控制效果,除储液晃动波高外,其他工况减震率均在40%以上,尤其体现在对层间位移角的控制。对于北京饭店地震动输入,地震动响应比较剧烈,此时组合减震B对地震动的控制效果要好于组合减震A。图3示出阻尼力耗能时程曲线,可以看出,虽然组合减震A整体耗能比组合减震B多,但地震动响应的峰值在第80 s之前,组合减震B耗能比组合减震A多,说明此时组合减震B对地震动响应的削峰效应比组合减震A要好,组合减震B对地震动的适应能力更强。所以需根据实际工程抗震要求、场地条件等情况,选择最合适的被动控制方式。
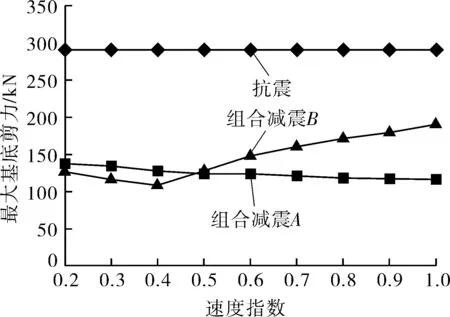
速度指数是影响黏滞阻尼器减震效率的主要因素之一,选取速度指数在0.1~1.0时,考察其对组合减震措施减震效率的影响。以El Centro波作为地震动输入,加速度峰值为0.2g,其结果如图4所示。

图3 阻尼力耗能时程曲线
(a)基底剪力

(b)倾覆弯矩

(c)层间位移角

(d)晃动波高
从图4可以看出,随着黏滞阻尼器速度指数的变大,采用组合减震B措施的基底剪力和倾覆弯矩先减小后增大,有优化区间;而采用组合减震A措施的基底剪力和倾覆弯矩随着速度指数的变大逐渐减小。无论采用何种减震方式,层间位移角和晃动波高都随着速度指数的变大而减小。因此需根据工程实际,从经济性和安全性两个方面考虑,选取最优的黏滞阻尼器速度指数。对本工程实例来说,组合减震A时,最佳速度指数为1.0;而组合减震B时,最佳速度指数为0.5~0.6。
立式圆筒型储液容器内储液的高度直接影响储液的晃动周期和结构的自振周期,关系到结构在地震作用下的动态响应,所以本节将按照25%储液、50%储液、75%储液、100%储液进行抗震和减震地震动响应研究,以0.2g峰值加速度的El Centro波作为地震动输入,对比分析两种组合措施在各种储液高度条件下的减震效率。隔震层周期取2 s,阻尼比为0.1,其计算结果见表7~10。

表7 25%储液下地震动响应结果

表8 50%储液下地震动响应结果

表9 75%储液下地震动响应结果

表10 100%储液下地震动响应结果
由表7~10可以看出,对抗震结构来说,储液较少时其地震动响应较大,随着储液高度的变化,地震动响应也出现起伏,说明储液长周期晃动能在一定程度上抑制结构地震动响应。随着储液高度的增加,S(S=Hl/R)越大,根据公式,储液晃动频率ωc越大,越接近地震动卓越频率,所以液体晃动波高也逐渐变大。建议对高举架立式圆筒型储液容器进行抗震设计时,宜采用空罐设计,计算结果可偏于安全。
采用组合措施后,无论储液量为多少,均能大幅削弱高举架立式储罐的地震动响应。采用组合减震A时,随着储液高度的增加,其地震动响应也呈增大的趋势;而采用组合减震B时,其地震动响应峰值随储液高度的增加变化不大,说明储液高度的变化对组合减震B减震效率的影响相对较小。
2 有限元数值仿真分析
2.1 有限元模型的建立

图5 有限元模型
以上述工程实例,基于有限元软件ADINA建立有限元模型,罐壁及底板均采用四节点等参壳单元,平台板采用三维实体单元,液体采用三维势流体单元,梁柱采用空间Beam单元。隔震层采用弹簧单元模拟,简化为平动的弹簧和阻尼。黏滞阻尼器采用非线性Spring单元,只需设置阻尼系数及速度指数,此时同样忽略阻尼器质量及支撑刚度的影响,假设其只输出阻尼力。由于所选用的工程实例中支承有一定的倾角,水平截面呈正六边形,所以应先计算出附加斜撑式黏滞阻尼器分别与x,y,z轴的夹角;进而计算出各轴所需的阻尼系数分量;再分别设置x,y,z方向上的非线性Spring单元。所建模型如图5所示。
2.2 数值仿真分析
以峰值加速度为0.2g的El Centro波作为地震动输入,对高举架立式圆筒型储液容器有限元模型进行地震动响应,并与理论值进行对比。计算结果如表11及图6所示。

表11 El Centro地震波作用下数值仿真结果
从图6中可以看出,两种减震方式对地震动响应均能起到较好的控制效果。采用组合减震措施后支柱竖向反力、基底剪力大幅减小,尤其对支承结构层间位移角的控制更为明显,所以考虑组合减震措施后,支承结构可降烈度设计;且基础部位不会产生上拔力,能优化基础设计。两种减震方式均对储液底部的刚性质量分量有较好的控制作用,而对晃动分量控制有限。从整体上看,两种组合减震措施的减震效果相差不大。

(a)晃动波高
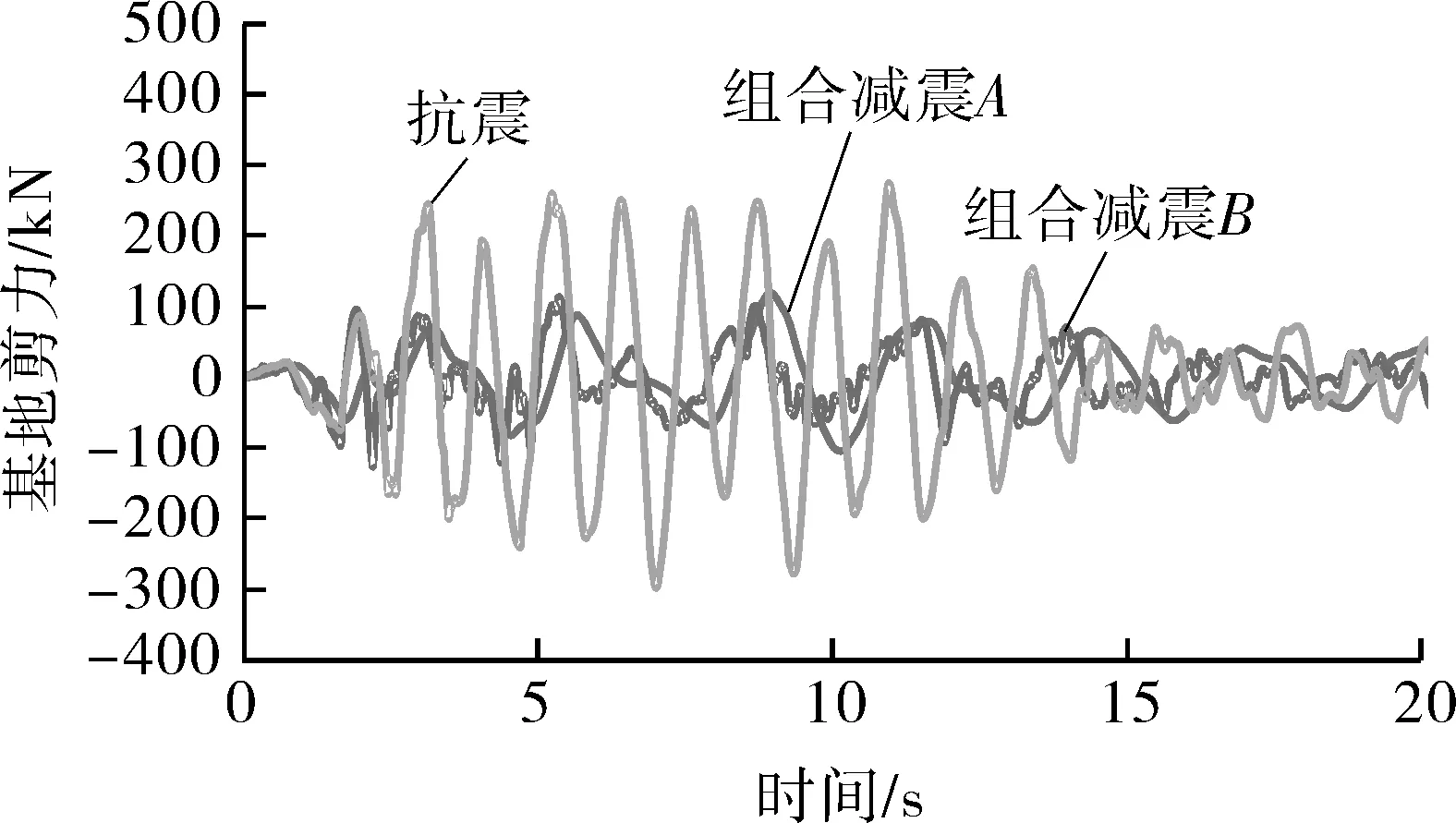
(b)基底剪力

(c)竖向反力
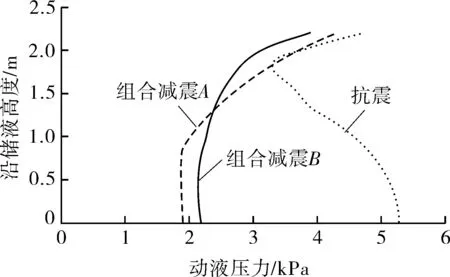
(d)动液压力

(e)隔震层位移

(f)耗能时程
从图6(e)中可以看出,采用组合减震B时,隔震层水平位移比采用组合减震A时要小得多。说明采用组合减震B,有利于保护隔震层,不至于偏移过大而造成的隔震层失效,且有利于结构的安全。
图6(f)为第5层某一x方向黏滞阻尼器输出的阻尼力耗能时程曲线,可以看出,采用组合减震B时,黏滞阻尼器消耗了更多的能量,使黏滞阻尼器充分发挥作用,配置更加合理,减震效果更好。
3 有限元解与理论解对比分析
以金门公园、北京饭店、El Centro和Pasadena波作为地震动输入,对高举架立式圆筒型储液容器地震动响应的有限元解和理论解进行对比分析,峰值加速度为0.2g,其计算结果如表12,13所示。

表12 组合减震A模型理论解与有限元解峰值绝对值对比
注:差异率=(有限元解-理论解)/有限元解
从表12,13中可以看出,理论解与有限元解十分接近,除表13中Pasadena波输入时晃动波高差异为33.00%,其余工况值最大差异率不超过15%,验证了理论模型与有限元模型的正确性,也说明本文采用的建模方法是行之有效的。

表13 组合减震B模型理论解与有限元解峰值绝对值对比
4 结论
(1)对于不同地震动输入,两种组合减震措施均有较好的减震效果,组合减震B对地震动的适应能力更强。采用组合减震B时,隔震层偏移较小,不至于偏移过大而造成的隔震层失效,有利于保护隔震层,也有利于结构的安全;同时在此种组合形式下,黏滞阻尼器消耗了更多的能量,使黏滞阻尼器充分发挥作用,配置更加合理,减震效果更好。
(2)需根据工程实际,从经济性和安全性两个方面考虑,选取最优的黏滞阻尼器速度指数。对本工程实例来说,组合减震A时,最佳速度指数为1.0,而组合减震B时,最佳速度指数为0.5~0.6。
(3)模型理论解与有限元解比较接近,相互验证了理论模型与有限元模型的正确性,说明本文采用的建模方法是行之有效的。

