采空区残余倾斜变形对路基稳定性的影响分析与评价
王猛
(1.山东省鲁南地质工程勘察院,山东 济宁 272100;2.自然资源部采煤沉陷区综合治理工程技术创新中心,山东 济宁 272100;3.山东省地质矿产勘查开发局采煤塌陷地综合治理工程技术研究中心,山东 济宁 272100)
0 引言
地下煤层被采出后,开采区域周围的岩体原始应力平衡状态遭到破坏,应力会重新分布,达到新的平衡。在此过程中,岩层和地表会产生持续的移动、变形,甚至非连续性的破坏(开裂、冒落等),相关研究表明,由于地下开采导致的地表持续移动时间可达几年甚至几十年[1-5]。随着我国城镇化进程的加快,采煤塌陷区逐渐融入城市发展建设地块之内,越来越多的建筑工程,如房地产开发项目、高速公路、高速铁路、输油管线、供电线路等,要穿过或位于采煤沉陷区之内[6]。地下开采造成的地表残余变形对公路路基的稳定性影响较大。在采空区公路建设项目的规划设计阶段,必须对路基的稳定性进行评价,并根据评价结果,合理调整公路路基的设计参数。
针对公路路基的稳定性评价,宋杨等[7-12]运用有限元数值模拟,对路基边坡稳定性进行计算分析,并根据参考结果调整路基设计参数和制定防护措施。这种方法的可靠性和准确性取决于路基填料力学性质参数(如容重、内摩擦角等)及所建力学模型的准确性,而力学模型的建立受人为影响因素较大,该方法目前大多用来对拟建公路设计参数的合理性进行定性分析,或作为其他方法的补充和参考。黄云川等[13-15]基于力学平衡原理,通过计算最不利滑动面抗滑力和下滑力,进而得到公路路基稳定性系数,根据稳定性系数对路基稳定性进行评价。这种方法已应用于大量的工程实践,积累了丰富的实际经验,是当前常用的路基稳定性评价方法。魏见海等[16-19]对采空区公路路基的稳定性进行了相关研究,但并未分析地表残余变形对公路路基的稳定性影响机理,也未从力学平衡的角度对残余变形导致的路基稳定性变化进行研究。
1 采空区地表残余变形的计算方法
地表移动变形计算方法可分为典型曲线法、负指数函数法、概率积分法和数值计算分析法等,其中最为常用的方法为概率积分法,该方法已成为国内较为成熟,应用最为广泛的地表移动变形预测方法。概率积分法是影响函数法的一种,以正态分布函数为影响函数,用积分式表示地表下沉盆地形态特征[20]。
对于水平煤层或缓倾斜煤层,地下开采导致的地表任一点(坐标为(x,y))的稳态下沉值W(x,y)、沿x和y方向的稳态倾斜值ix和iy可表示为:
式中:Wcm—充分采动条件下地表最大下沉值(mm);r—主要影响半径(m);u,ν—开采单元在x,y方向上的坐标值(m);D—开采区域几何范围。
地表移动变形的动态变化过程可以使用含有时间变量的函数表示,Knothe时间函数可以准确描述地表移动变形的动态过程,该时间函数可表示为[4]:
φ(t)=1-e-at
(2)
式中:a—与采矿地质条件有关的时间因素影响系数,一般为2.0;t—预计时刻与工作面停采时刻之间的时间间隔(年)。地表任一点(x,y)在t时刻的动态下沉值W'(x,y,t)及动态倾斜值i'x(x,y,t),i'y(x,y,t)可表示为:
(3)
将式(1)与式(3)相减,即可得到地表任一点(x,y)在t时刻的残余下沉值ΔW(x,y,t)及残余倾斜值Δi'x(x,y,t),Δiy(x,y,t):
(4)
根据上述原理,基于概率积分法的地表残余倾斜变形值计算过程可描述为:①使用概率积分法计算地表任一点的最终倾斜变形值;②结合Knothe时间函数计算地表点在t时刻的动态倾斜变形值;③将地表点的最终倾斜变形值与动态倾斜变形值作差,即可得到地表点的残余倾斜变形值(图1)。
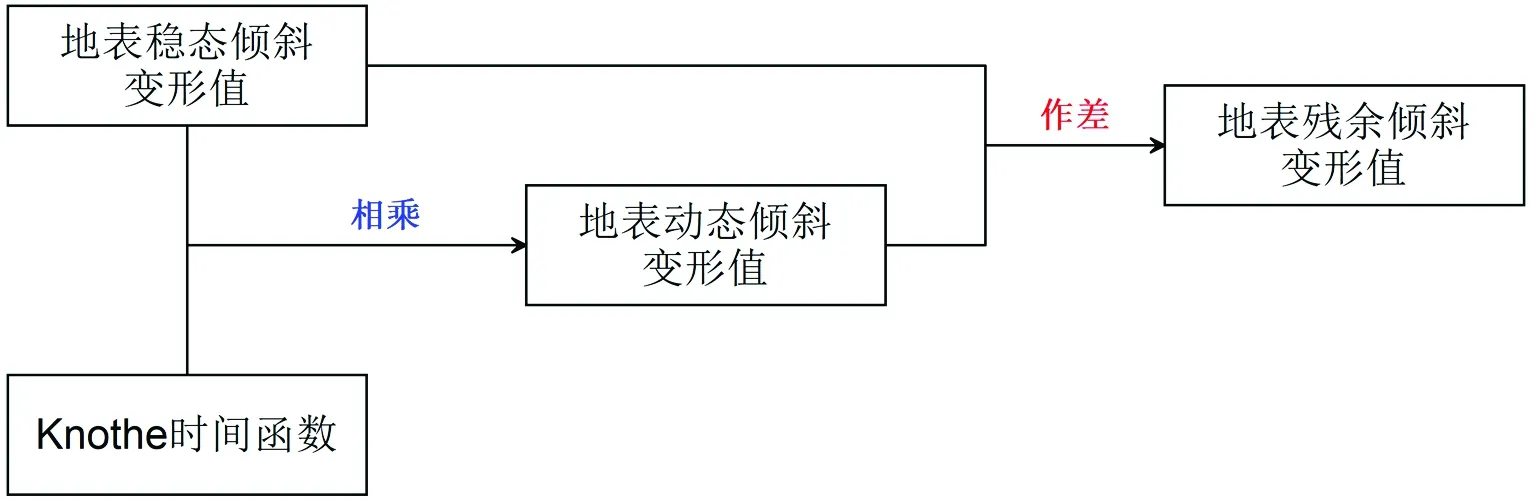
图1 地表残余倾斜变形计算流程图
2 采空区路基稳定性评价方法
2.1 条分法路基稳定性系数计算
我国常用路基稳定性评价方法为条分法,通过计算路基稳定性系数,对路基的稳定性进行评价。当以带有黏性的土填筑路基时,路基滑塌破裂面的形状通常为一圆弧状滑动面(图2)。ABCD为一采空区拟建公路路基,其滑动坡面假设为以O为圆心,AC为滑动坡面的圆弧,将圆弧AC分为N段条状土体,假定每一段土条两侧的侧向力与土条底部切线平行并相互抵消,则土体沿圆弧滑动面下滑的稳定性系数K可表示为[15]:
(5)
Ni=Qi·cosαi=γbihi·cosαi
(6)
Ti=Qisinαi=γbihi·sinαi
(7)
式中:γ—路基填料的湿容重(kN/m3);c—路基填料的粘聚力(kPa);φ—路基填料的内摩擦角(°);αi—各段土条滑动圆弧切线的倾角(°);L—滑动圆弧全长(m);bi—各段土条宽度(m);hi—各段土条高度,包括路堤顶部车辆荷载的换算土柱高度(m)。
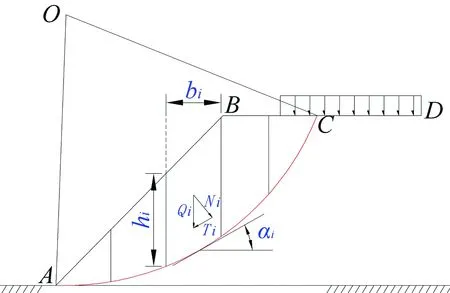
图2 条分法圆弧滑动面路基稳定性系数计算示意图
在公式(5)中,分子为滑动土体的总抗滑力,分母为滑动土地的总下滑力。当路堤不受采空区残余变形影响时,无论怎样对设计路堤选取滑动面,总抗滑力总是大于总下滑力,即路基稳定性系数K>1,路基能够保持稳定状态。采空区残余变形会使滑动面倾角发生变化,可能导致路基稳定性降低;如果地表残余变形导致的路基稳定性系数K<1,路基就会沿滑动弧面发生滑动,从而对公路主体结构造成严重破坏。
地下煤层的开采会造成地表倾斜,进而引起路基滑动面的倾角发生变化。设由于开采造成的地表残余倾斜Δi引起的滑动面倾角变化量为Δα,则:
(8)
式中:ρ—圆弧滑动面的半径(m)。由于地表倾斜引起的土体重力垂直和平行于滑动面的分力Ni,Ti的变化分别为:
Ni=Qi·cos(αi+Δα)
(9)
Ti=Qi·sin(αi+Δα)
(10)
可见,当采空区地表残余倾斜方向与滑动方向相同时,即Δα>0,土体下滑力增大,抗滑力减小,路基稳定性系数K值降低;反之,如果采空区地表残余倾斜方向与滑动方向相反,则土体下滑力减小,抗滑力增大,路基稳定性系数K值增大,此时,在一定程度上有利于采空区公路建设。使用条分法验算圆弧滑动面路基稳定性系数时,每一个假设的滑动面均可求得相应的路基稳定性系数;通常情况下,需要选取几个最不利滑动面分别计算路基稳定性系数,如果各滑动面中的最小路基稳定性系数≥1.25时,则可以认为路基是稳定的。
另外需要说明的是,平缓、均匀的地表残余下沉和残余水平移动会使上方建(构)筑物发生整体移动,一般不会对道路路基稳定性产生影响。地表残余曲率和水平变形虽然会在一定程度上造成路基承载力的降低,但是其影响十分有限,通常可以忽略不计。
2.2 最不利圆弧滑动面的解析法求解
使用条分法验算圆弧滑动面路基稳定性系数的关键在于最不利滑动面位置的确定,而最不利滑动面的位置可根据最不利圆弧滑动面圆心的位置来确定。实际经验和相关研究表明,4.5H法在边坡稳定性验算中精度较高,也更加贴合实际情况。
如图3所示,某梯形路基断面为ABCD,路基高度和边坡坡率分别为H,k,在坡脚点A建立如图所示的坐标系,则A,B,F点的坐标可表示为:
(11)
在坡脚点A作与一与边坡夹角为β1的直线AO;在路基顶点B做与路基顶水平线成β2的直线BO;β1,β2为与边坡坡率有关的角度,则AO,BO可表示为:
(12)
设直线AO,BO的交点为O(xO,yO),则有:
(13)
O点即为路基填料内摩擦角φ为0时(如软黏土)的最危险滑动圆圆心位置,当填料内摩擦角大于0时(如砂质黏土等),最危险圆心的位置在FO方向的延迟线上,即:
(14)
在该延长线上分别选择几个点作为最不利滑动圆弧的圆心,采用条分法,分别计算各圆心对应的滑动圆弧的路基稳定性系数,其最小值即为该路基的稳定性系数值。
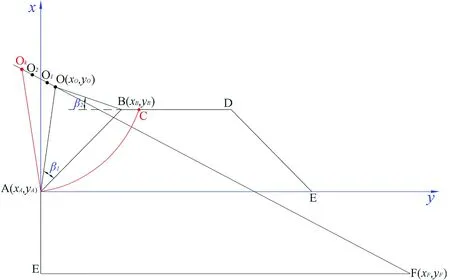
图3 4.5H法最不利圆弧滑动面圆心确定示意图
3 路基稳定性评价软件的设计与实现
基于上述原理,使用C#语言编制了采空区路基稳定性计算软件(图4)。该软件主要由用户交互模块、残余变形计算模块、路基荷载当量高度计算模块和条分法稳定系数计算模块构成,软件整体架构如图5所示。用户交互模块主要为软件主界面,该模块的主要功能是获取路基稳定性计算所需的各种输入参数,如:地表残余变形值计算数据、路基荷载当量数据、路基参数及填料力学性质参数等。残余变形计算模块可根据用户输入的评估区稳态变形预测值数据文件及动态变形预测值数据文件,使用距离加权反比例插值的方法计算地表任一点的残余倾斜值。评估区稳态、动态变形预测值数据文件,可使用山东省鲁南地质工程勘察院设计开发的SODP软件获得,也可将实测值按照SODP软件预测结果文件的格式生成相应的输入文件[21]。路基荷载当量高度计算模块可根据公路车道设计参数及车辆荷载参数将荷载换算为填料土柱高度。将地面点的残余倾斜值和路基荷载当量高度输入条分法稳定系数计算模块即可解算出地面点的路基稳定性系数。
首先根据评估区地下煤层的地质采矿参数及评价时间计算评估区的稳定、动态变形值,通过插值获得评估点的残余倾斜值。然后根据公路荷载当量设计参数及填料容重,计算公路荷载的换算土柱高度。根据最不利圆弧滑动面解析公式,计算圆心及圆弧长度,并根据计算的土条数进行土柱划分。根据残余倾斜值和荷载换算高度,分别计算每条土柱的抗滑力和下滑力,进而得到评估点路基的稳定性系数(图6)。
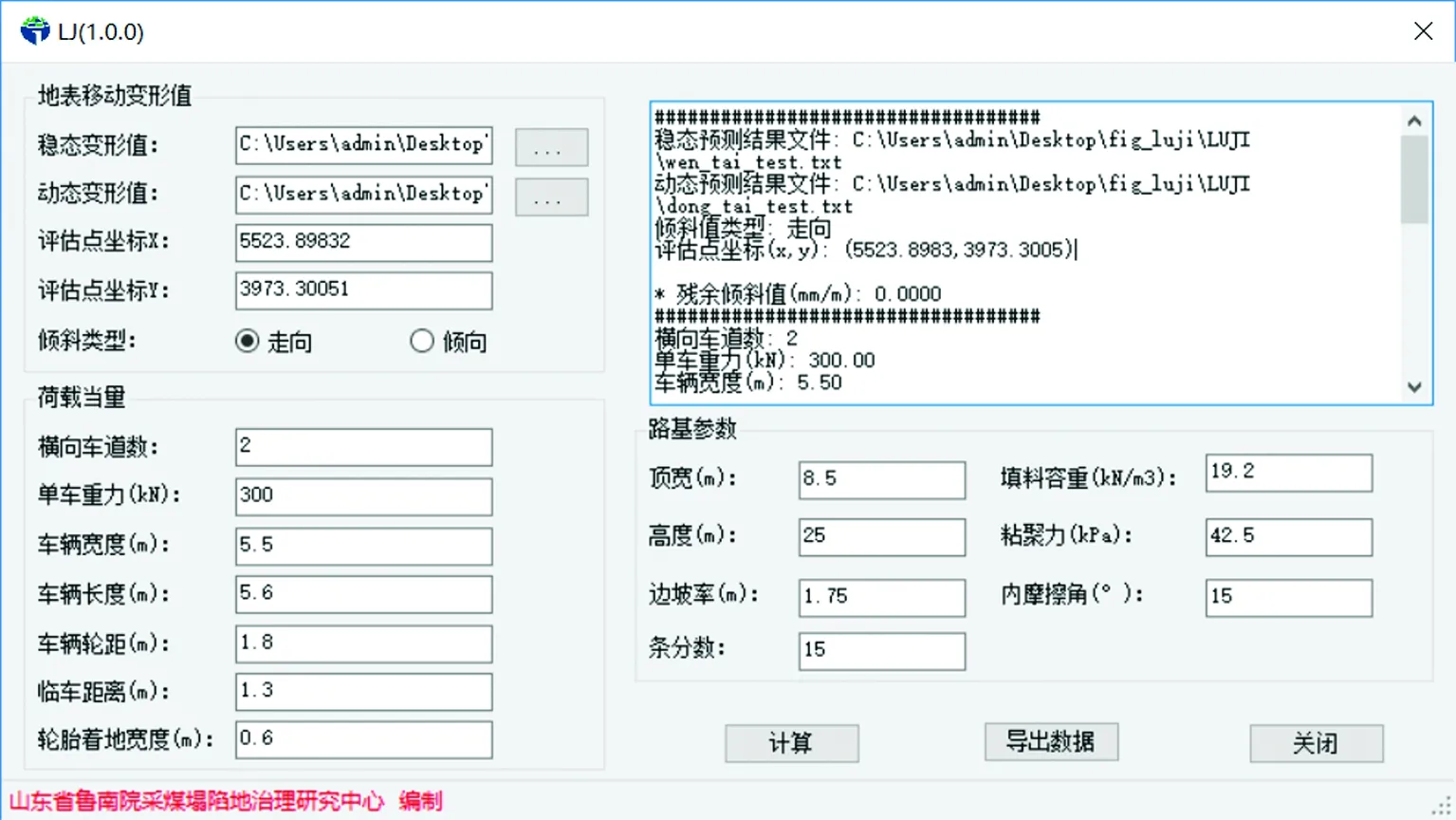
图4 路基稳定性计算软件主界面
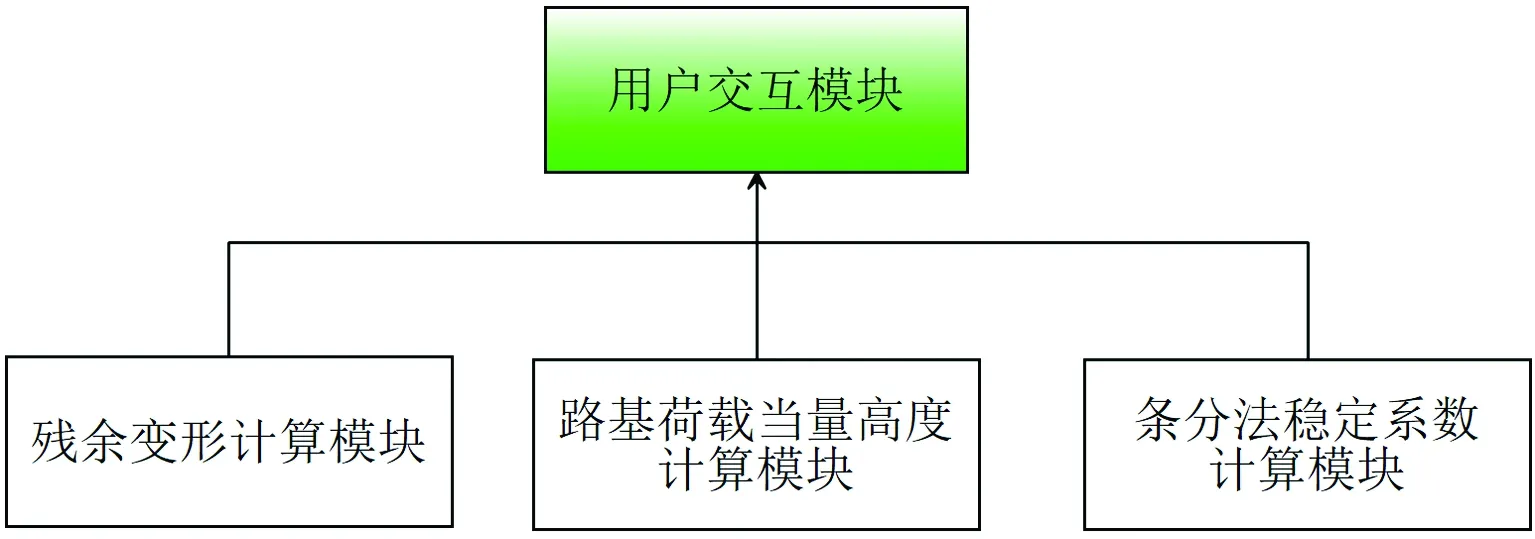
图5 路基稳定性计算软件整体架构设计
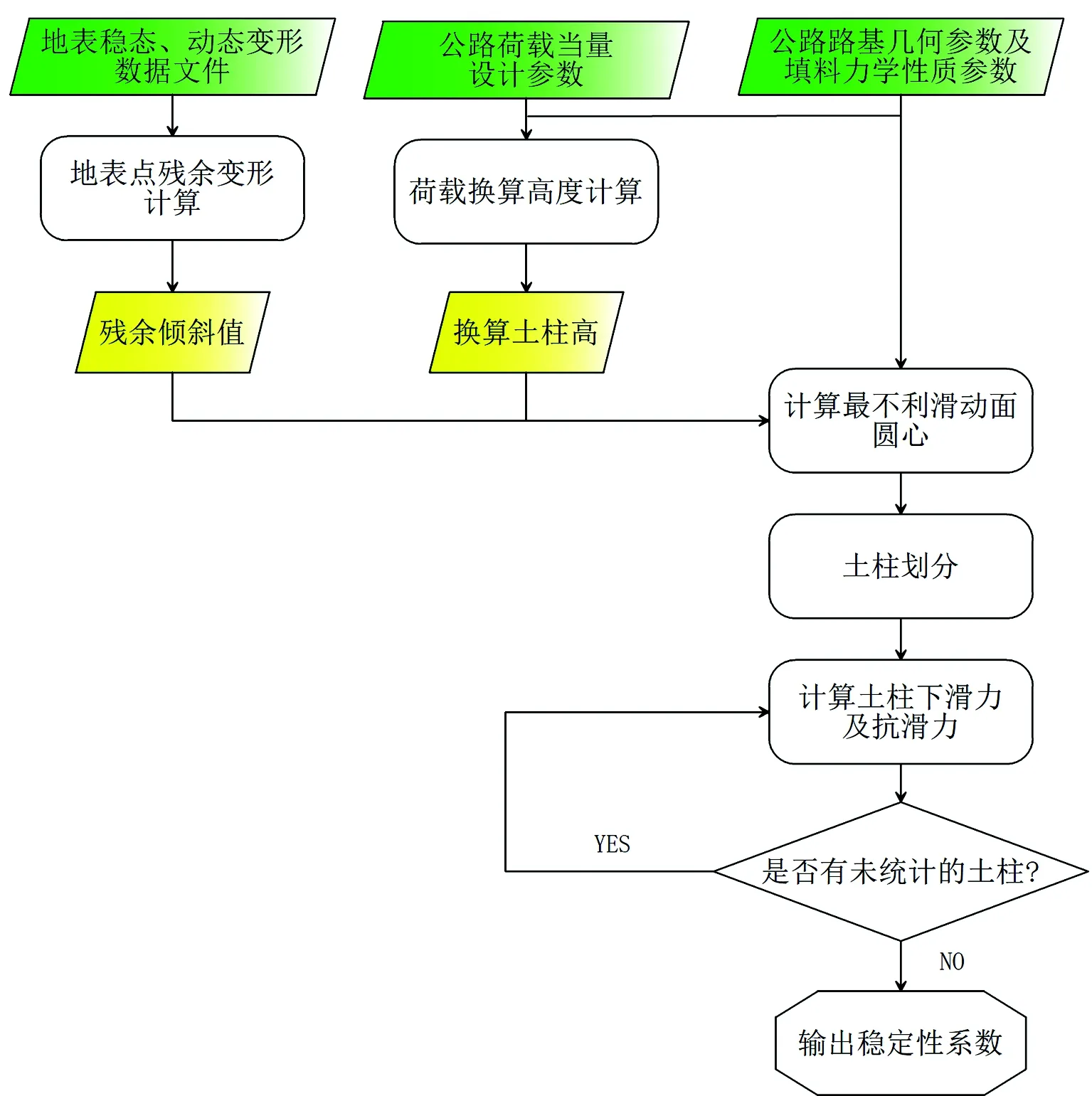
图6 路基稳定性计算软件算法流程图
4 验证与分析
4.1 项目简介及验证
某一公路建设项目穿越煤矿采空区正上方[注]山东省鲁南地质工程勘察院,济宁市快速路工程(一期)煤矿采空区场地稳定性分析与评价,2018年。,公路设计为7.0m的双车道,行车荷载为汽车-20级的重车(单车荷载为300kN);公路路基顶宽为8.5m,高度为20m,路基边坡坡率为1∶1.75;路基填料容重为19.2kN/m3,单位黏聚力为42.5kPa,内摩擦角为15°。拟建公路下方采空区由呈东—西方向布置的2个工作面(2311和2312)组成,2311工作面于2017年4月回采,2017年9月停采;2312工作面于2017年12月回采,2018年5月停采。采空区最大宽度336m,最大长度771m。回采工作面所采煤层为3煤,工作面平均采深-300m,平均采厚8.5m,煤层倾角1.5°。根据该矿地表移动变形观测资料,确定采空区概率积分法预测参数(表1)。
拟建公路计划于2020年6月开工建设,为了评估该路段采空区残余变形对拟建公路的影响,需要对公路路基稳定性进行分析和评价。以2020年6月作为预测基准日期,使用SODP软件,用残余变形预测方法对采空区残余变形进行预测,得到评估区垂直于公路中线方向的残余倾斜值(图7)。

表1 采空区概率积分法预测参数
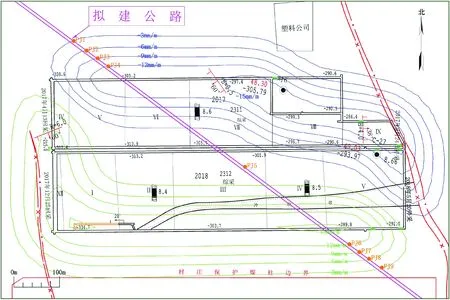
图7 建设项目位置及地表残余倾斜图
在采空区公路路段上随机取一系列点,用图解法计算这些点的路基稳定性系数,并与软件计算结果进行对比。以该路段上的PJ5点(残余倾斜值为0mm/m)为例,将土柱条分数设置为15条,使用图解法求得该点荷载换算高度为1.0m,最不利圆弧半径为36.2m,弧长为51.1m,路基稳定性系数为1.27。使用该文提出的方法进行计算,结果如图8所示。可以看出,图解法和文章中提出的解析法计算的结果是一致的。
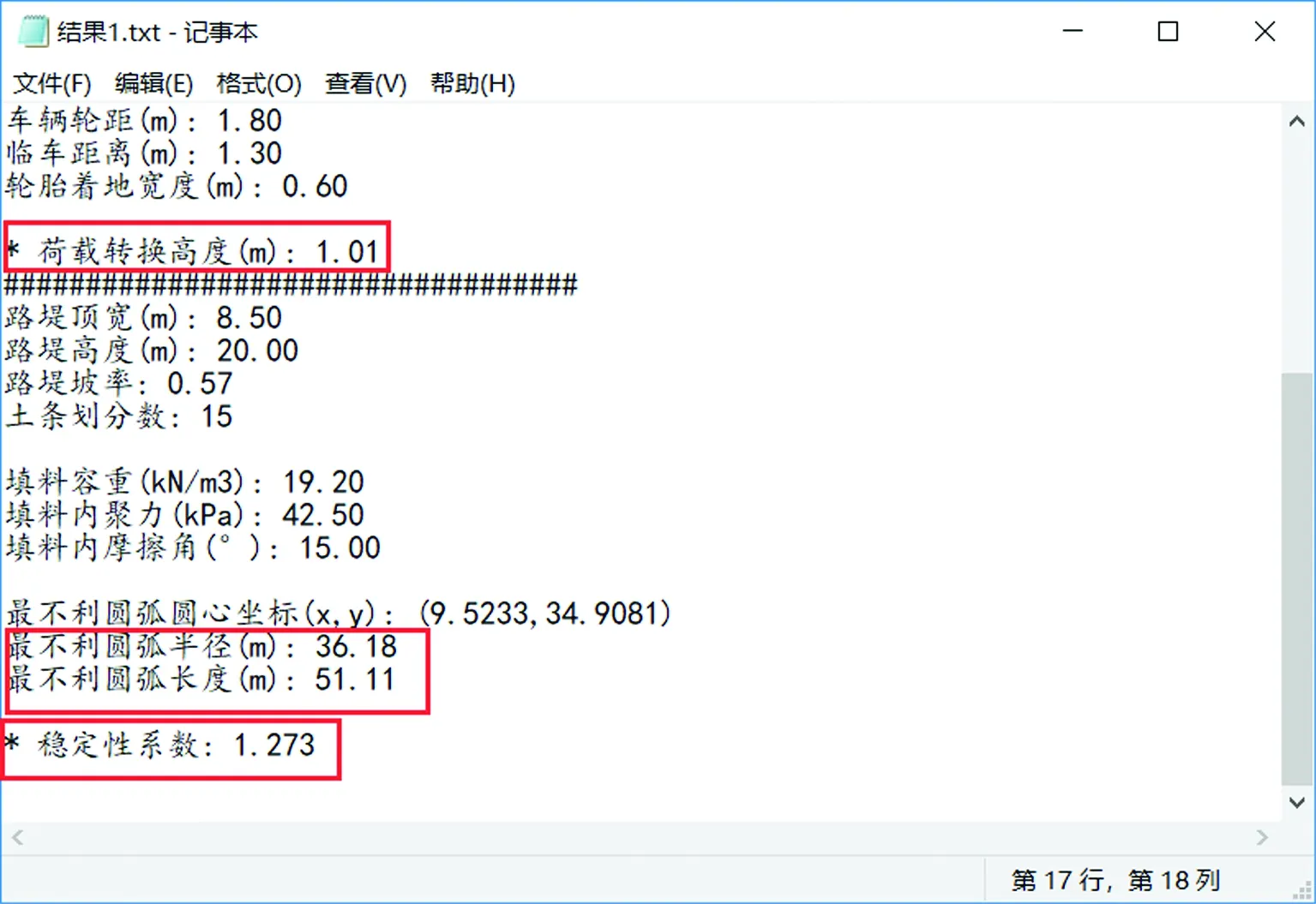
图8 路基稳定性计算软件计算结果图
4.2 地表残余倾斜对采空区路基稳定性的影响
为了分析采空区地表残余变形对路基稳定性的影响,选择该拟建路段上的9个评估点PJ1-PJ9(相对坐标及残余变形值如表2所示),按照拟建公路设计标准分别计算这些点的稳定性系数。评估点稳定性系数的计算结果如图9所示。
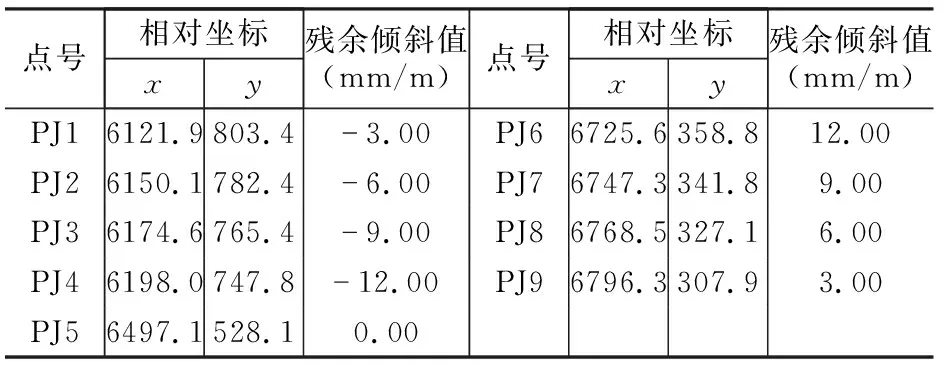
表2 评估点相对坐标及残余倾斜值
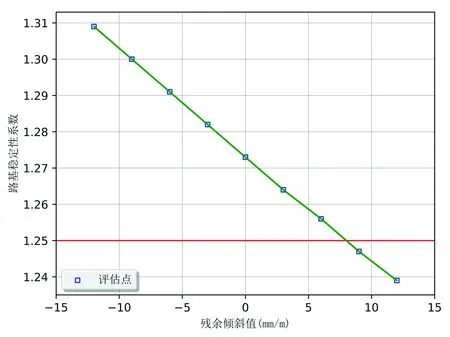
图9 不同残余变形的路基稳定性系数图
可以看出,随着地表残余倾斜值的增加,路基稳定系数大致呈线性降低。当地表倾斜方向与路基坡体滑动方向相反时(残余倾斜值为负),路基坡体的稳定性系数随着残余倾斜值的降低而增加,即地表残余倾斜有利于该坡体面的稳定;当地表倾斜方向与路基坡体滑动方向相同时(残余倾斜值为正),路基坡体的稳定性系数随着残余变形值的增加而减少,即地表残余变形对该坡体面的稳定性不利。当地表残余倾斜大于7.5mm/m时,路基稳定性系数小于1.25,该路基的设计参数不能满足稳定性的要求,若按该方案进行施工,极有可能造成路面滑坡事故。
4.3 路基坡率对路基稳定性的影响分析
为了分析路基坡率对路基稳定性的影响,选择PJ6点(残余倾斜值为12mm/m),分别设置不同的路基坡率,且其他路基设计参数不变,分别计算不同坡率下该点的坡体稳定性系数,计算结果如图9、表3所示。
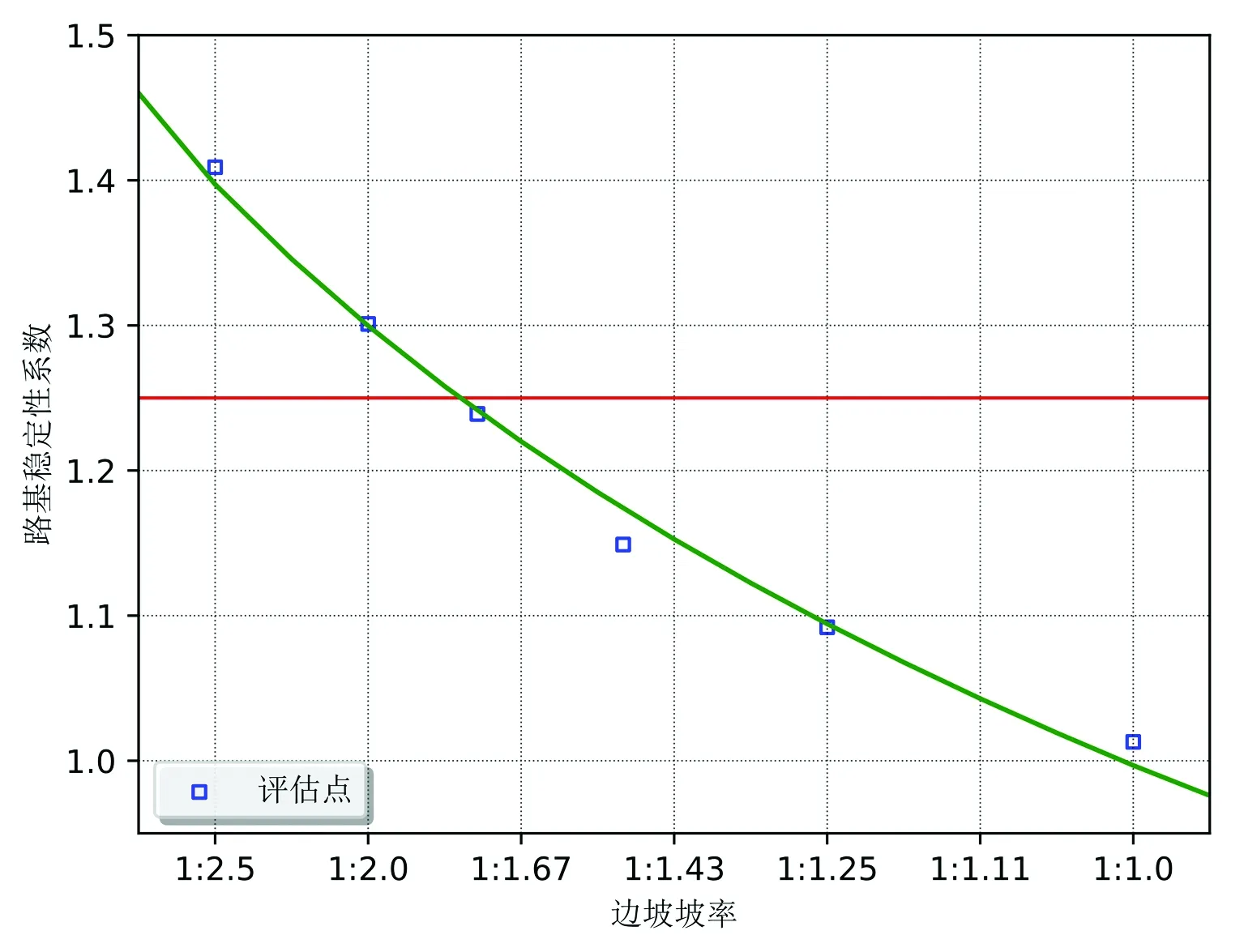
图10 不同坡率的路基稳定性系数图

路基坡率1∶11∶1.251∶1.51∶1.751∶21∶2.5路基稳定性系数1.0131.0921.1491.2391.3011.409
可以看出,随着路基坡率的增加,路基稳定性系数呈对数形式降低;当路基坡率大于1∶1.78时,评估点的路基稳定性系数小于1.25,该路段极有可能出现滑坡。随着路基坡率的降低,路基稳定性系数迅速增加,即通过降低路基高度,增加路基底宽的方法,可以有效提高公路路基的稳定性。
5 结论
针对采空区公路建设项目的路基稳定性评价,提出了基于概率积分法和Knothe时间函数的采空区残余倾斜变形计算方法,分析了路基稳定性的条分法计算原理和采空区残余倾斜变形对采空区路基稳定性的影响机理。根据4.5H法路基最不利滑动圆弧的确定方法,推导了基于解析法的路基最不利滑动面计算公式,并使用C#语言对提出的计算方法进行了编程实现,研发了相关计算软件。通过工程实例,就提出的方法和编制的软件进行了验证,并对地表残余倾斜、路基坡率对采空区路基的稳定性影响进行了分析,得出以下结论:
(1)路基稳定性系数与采空区地表残余变形值呈反比,随着地表残余变形值的增加,路基稳定性系数呈线性降低;当地表残余倾斜方向与路基滑动方向相同时,路基稳定性系数降低;当地表残余倾斜方向与路基滑动方向相反时,路基稳定性系数增大。
(2)路基稳定性系数与路基坡率呈反比,随着路基坡率的增加,路基稳定性系数呈对数形式降低;通过降低路基高度或增加路基底宽可以有效提高采空区公路路基的稳定性。

