关于多路t-EBPSK 联合调制的抗干扰性能研究

王申元

（中国民用航空华北地区空中交通管理局，北京 100621）

本课题就多路超窄带t-EBPSK 联合调制进行研究，研究其调制解调性能。超窄带最大的特点就是传输带宽足够窄，相同带宽中可以传输更多的信号，但是当复合多路调制的过程中，除了考虑信号所占带宽的宽窄外，当多路复合时，信号间间隔多大才会获得比较好的抗干扰性能也是十分值得考虑的。本课题主要是针对这个问题，通过matlab 仿真，来实现信号多路复合的模拟，观察并研究超窄带信号多路复合时，信号直接需要多大带宽才能实现信号抗干扰性最佳。

1 t-EBPSK 多路复合

当两路信号进行多路复合时，具体实现思路可以描述为图1。

图1 实现两路信号多路的模型

具体实现步骤如下：

（1）利用randint 函数产生两路随机信号，由于后面设计到多个循环，数据太多会使整个程序运行过慢，所以选用两路分别包含100个“0”“1”信息的信号。经过代码编写，可以得到这两路信号如图2所示。

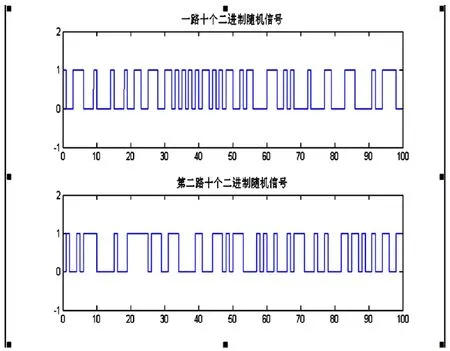
图2 产生的两路随机信号

（2）和一路信号一样，根据参考文献[1]公式进行模拟仿真，经过t-EBPSK 方式调制上面的两路信号可以得到图3的调制波形。

同样数值设置如下：A=1；B=1；T=1；K=0.1；Tc=0.04；T=25*Tc；w=2*pi/Tc；tao=K*T；

（3）对两路信号进行搬移并相加

通过查阅参考文献[2]得知，对两路信号分别乘以余弦信号，即可实现对信号在频域上的搬移，由于采用间隔的取值，信号的频域范围为200Hz。这里对w 的设置分别为30和15 。

搬移成功后对两路信号进行相加进入信道，及用awgn 函数产生噪声，可以得到图4的功率谱图。

图3 经t-EBPSK调制后的两路波形

图4 两路信号的功率谱和搬移后相加后功率谱

（4）用带通滤波器对两路信号进行分离

分离的第一步是对相加后的信号与余弦函数相乘，可以得到得到两路信号的功率谱如图5所示。

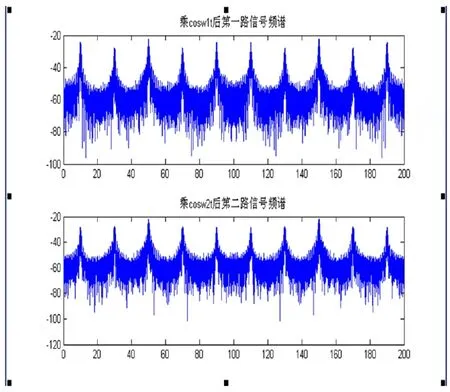
图5分离后的两路信号的功率谱图

在对滤波器的选择方面我进行了分析与判断，首先了解IIR和PIR 的区别。

先大体介绍下IIR 滤波器的几个特点：

（1）IIR 数字滤波器的系统函数可以写成封闭函数的形式。

（2）IIR 数字滤波器采用递归型结构，整个结构有反馈的环路，而且整个运算结构由延时、乘以系数等基本运算，而且有多种不同的结构形式，包括直接型、正准型等，并且所有的形式都有相应的反馈回路。此外，在实际运算的过程中存在舍入的处理，这会使得误差不断的累计，从而产生寄生振荡。

（3）IIR 数字滤波器在设计的过程中，接住了模拟滤波器的成果，而且有现场的数据进行参考，所以说整个设计的工作量不是很大，设计的工具要求不是很高。因此，在设计滤波器的时候直接根据相应的指标写出公式，然后进行转变，得到数据滤波器的公式。

（4）IIR 数字滤波器对相位的要求相对较高，所以说其相位特性控制难度较大，需要额外增加相位校准网络对其进行控制。

利用MATLAB 进行IIR 滤波器设计的时候，可以充分的发挥Butterworth 函数的特点和优势，进而设计出巴特沃斯滤波器，而通过Cheby1函数则可以设计出契比雪夫I 型滤波器，两种滤波器有着各自的特点和优势。相比FIR 滤波器来说，IIR 滤波器在设计的过程中其阶数不是由设计师决定的，而是通过设计师对各种不同的参数进行输入，由软件自动设计出符合相关参数的滤波器。

对IIR 滤波器进行介绍之后然后对两种滤波器进行对比，首先，从性能方面来说，IIR 滤波器传递的函数有零点和极点两组因素进行控制，但是极点的限制仅仅是在一个单位元中。因此，可以通过低阶数获得更高的选择性，同时提高整体的效率，而高效率是需要将非线性作为代价换取而得到的，同时选择性越好，其非线性情况越为严重。FIR 滤波器传递函数的极点是固定的，在原点不能移动，只能通过改变零点的位置来实现它性能的改变，为了达到更高的选择性，需要选择较高的阶数，所以说对于同样的滤波器设计指标来说，FIR 滤波器需要的阶数要高IIR 滤波器5到10倍，这就在很大的程度上提高了成本，同时信号的延迟也相对较大。如果单单从线性相位的要求来说，IIR 滤波器必须有全通网络对其进行校正，同时会在很大的程度上增加其阶数和复杂性，但是FIR 滤波器直接可以得到相对严格的线性相位。从结构上来看，IIR 滤波器需要充分的利用递归结构进行极点的合理培之，从而确保极点处于单位元之内，但是受到有限字长效应的影响，其在实际运算的过程中需要进行一些舍入的处理，这会引起极点发生偏移，降低滤波器的稳定性，甚至会引起寄生振荡。与IIR 相反的是，FIR 滤波器只需要采用递归结构，不会存在不稳定性的情况，所以说出现频率特性的可能性非常小。此外，FIR 滤波器还可以利用傅里叶变化算法，可以有效的提高计算速度。除此之外，IIR 滤波器的设计结构相对简单，但是在实际设计的过程中会存在分段常数特性的滤波器，包括低通、高通等等，这些都与模拟器滤波器有很大的联系。相比IIR 滤波器，FIR 更加灵活，而且应用范围更为广泛，在一些特殊的场景都可以充分的发挥其特点和优势。当然，两种滤波器也有一些共同的地方，无论是哪种滤波器，随着其阶数的不断增加，其信号的延迟也会越大；此外，随着阶数越高，对系数精确度的要求也越高，不然会出现极点偏移到圆外，所以说，在阶数的选择上需要综合多方面的因素进行考虑。

通过上文的对比分析发现，IIR 和FIR 滤波器有着诸多不同之处，在实际使用的过程中需要根据实际情况进行选择，从而确保滤波器功能的充分发挥。在一些不是很敏感的情况下，可以选择IIR 滤波器，例如在一些语音通信deng 的场合中，而对于图像通信这种需要大量数据传输的系统，对线性相位的要求较高，所以说选择FIR 滤波器更为合适。总的来说，在实际应用的过程中根据实际情况，并结合滤波器的特点和优势，综合多方面因素选择合理的滤波器。根据本课题的设计需求，阶数过大会对信号产生很明显的时延，综合考虑各方面因素，我最终采用的FIR 滤波器。

wsl=0.46.*pi；wpl=0.48.*pi；wph=0.52.*pi；wsh=0.54.*pi；

DB=wpl-wsl；

N=ceil（12.*pi./DB）；

wc=[（wsl+wpl）./2./pi，（wph+wsh）./2./pi]；

hn=fir1（N-1，wc，blackman（N））；

调制运行上述代码可以产生比较理想的滤波器特性如图6。

图6 带通滤波器的幅度和相位图

对于信号经过滤波器则使用已知函数filter。滤波器的使用同时也带来了时延问题，对时延多久，如何减少时延对信号解调的影响是一个比较关键的问题。通过查阅参考文献[3]，得到了相关解释：我们知道，滤波在时域上表现为输入信号与系统冲激响应的卷积。以离散时间系统为例，若记x（n）为输入信号，h（n）为系统的冲激响应（出于实时处理的需要，假定系统是因果的，即n ＜0时，h（n）=0），则滤波器的输出可表示为y（n）=∑h（k）x（n-k）。在卷积求和式∑h（k）x（n-k）中，每一个求和项正好对应输入信号x（n）的一个时延分量x（n-k）。卷积和正好就是输入信号各个时延分量的加权叠加。这样就不难理解滤波器的时延效应了：相对于输入信号的波形，输出信号的波形确实有一定程度的滞后。在卷积求和式∑h（k）x（n-k）中，时延分量x（n-k）的权系数为系统的冲激响应在时点k 的样值h（k），这就意味着，输出信号的时延主要由样值h（k）较大的那些时点决定。一个极端的例子是，若冲激响应为冲激信号的时延信号，即h（n）=δ（n-n0），n0＞0，输出信号也是输入信号相应的时延信号x（n-n0）。

最终解决办法可以总结为：设滤波器阶数为N。对采样点的延迟就是N/2，N 为偶数；或者（N-1）/2，N 为奇数。然后在滤波器输出结果那里，直接从头去掉N/2或者（N-1）/2个点即可。

最终经过滤波器后可以得出最终的两路信号，如图7和图8。

图 7 经带通滤波器后的信号1和信号2的频谱

最终分离出信号再用对t-EBPSK 信号的方式分别进行解调。最终得出解调波形。

并且w1，w2 分别取值为30*2π 和10*2π，即在功率谱图上搬移30和10，观察分析此时的误码率与信噪比关系，得到图8的关系图。观察图中数据，当两路信号为20时，信噪比大于五后即出现了较好的解调效果。接下来我们进一步研究这两路信号解调误码率和距离之间的关系。

图8 两路信号在固定误码率与信噪比关系图

本课题的重点即为对t-EBPSK 这种调制技术的多路复合进行可行性分析通过改变信号搬移距离，观察搬移后两路信号的误码率来判断。

在搬移距离d=2时，误码率分别为0.2200和0.1800

d=3时，误码率分别为0.1500和0.1300

d=4时，误码率分别为0.0100和0.0200

d=5时，误码率分别为0.0000和0.0100

之后随着d 的增长，误码率基本趋于零，得出从d=3时开始是比较理想的距离。其中d 代表频谱中的距离。

这一系列的研究证实了t-EBPSK 作为EBPSK 改进，拥有其独特的优势，兼顾超窄带特性、解调同步和抗干扰要求。同时经过两路信号的多路复合仿真的研究，证实其在多路复合中也有着姣好的抗干扰性，可见其广阔的运用前景。

2 总结与展望

t-EBPSK 这种调制方式凭借其出色的抗干扰性和超窄带特性。其在军用和民用两个方面都有着广泛的应用。在民用，能够有效的提高电力传输的效率，例如DSL，modem，CATV，等应用。此外，在航空领域中，VHF 数据电台有着广泛的应用，其数据的传输可以达到384kb/s，而利用UNB 之后，可以将其传输速率达2Mb/s，这对航空电台的需求完全符合。在地域通信网络中，节点通信设备的数据传输可以达到52Mb/s，随着UNB 应用之后，其传输速率可以提升20～50倍，这对卫星通信的传输效率有很大的改善。在移动通信中，基站在发射信号的时候消耗的功率非常的大，在下行可以使用超窄带的方式对其进行调试，而且该方法也可以应用于无线广播电台之中，由于电视台的频率相对较高，通过这种方式可以有效的传输更多的媒体信息。在军事方面，超窄带技术也有着广泛的应用，相比传统的通信技术，能够有效的提高信息传输的效率，并保证信息的安全性，同时大大的提高传输信息的抗干扰能力。此外，在同样的带宽里面，UNB 系统的传输速率可以高出其他100倍左右，这满足如今军事信息量巨大的需求。除此之外，在军事方面的应用还包括短波高速通信，通过UNB 技术能够提高传输效率，并且解决当前通信低数据的重要问题。而且能够有效的屏蔽非军事通信，当前的短波猝发通信只能通过2.4kb/s 的modem 进行传输，传输一个大小为100kb 的文件需要七分钟左右，但是利用UNB 只需要7秒钟，充分的发挥了猝发通信的作用和优势。