基于双层线性规划模型对高温作业服装研究

姚吉，金冰慧，邢曜琛

基于双层线性规划模型对高温作业服装研究

姚吉，金冰慧，邢曜琛

（河北工程大学信息与电气工程学院，河北 邯郸 056038）

高温专用防护服可以有效保障工作人员的生命安全。通过利用热力学相关理论，定性和定量分析工作环境温度、各织物层的厚度、工作时间、织物层材质等因素间的关系，建立圆柱形非稳态导热模型，得到各层温度随时间变化的分布规律，从而确定各隔热层在隔热效果中所占的比例。结合温度分布规律，建立热传导速率、各织物层厚度之间的双层非线性规划模型。确定约束件，结合MALAB等工具，得到各层织物最优厚度的取值范围，为模型推广至防护服的研制提供理论和数值参考。

热传导速率；圆柱形非稳态导热模型；双层非线性规划模型；合参化一

高温作业属于高风险职业，长时间工作在高温环境下，对人体行为功能危害巨大[1]。因此，一件优质、隔热防护效果俱佳的高温专用服装，不仅可以有效保护高温工作人员的生命安全，同时也能够延长在高温环境工作的时间，这对高温职业性工作具有重要的作用，尤其在消防行业，高温防护服一直是研究的重点。通过对高温防护服的研究，为防护服的设计提供一定的理论依据和数值参考。高温专用服装通常是由三层织物材料构成，记为Ⅰ、Ⅱ、Ⅲ层。其中Ⅰ层与外界环境接触，Ⅲ层与皮肤之间存在空隙层，记为Ⅳ层。由于实际环境具有高风险性、多突发性，所以，本文只能借助假人在模拟环境测量得到的温度数据。基于此，对温度数据进行观察、分析和处理，得出其中各层温度随时间变化的规律。定性、定量地分析工作环境温度、各织物层的厚度、工作时间、织物层材质等因素间的关系，建立双层非线性规划的研究模型，并进行模型求解。

1 众多学者对高温防护服的相关研究

高温作业防护服一直都是研究的热点，大批学者已经对其进行过相关研究。在文献[2]、文献[3]中，通过建立一维热传导差分方程，得出各层温度的具体分布。在文献[4]中，通过借助多层非稳态热传导模型，推出各层厚度满足条件的分析解。在文献[5]中，利用厚度最小作为目标函数建立的单目标规划模型，得出各层厚度的最优解。在文献[6]中，基于改进的傅里叶热传导方程，从而研究各层厚度之间的关系。在文献[7]中，结合BP神经网络算法，对其温度分布规律进行研究。在文献[8]中，在插值拟合与遗传算法的基础上，对各层织物厚度进行设计。在文献[9]中，采用有限差分与二分法结合的方法，对各织物层温度分布规律及厚度问题进行研究……总而言之，随着科学与技术的发展，对高温防护服研究、设计的趋势是不断向前，具有进步性、技术性、科学性。

2 建立圆柱形非稳态导热模型研究各织物层温度分布规律

研究思路：对各织物层分布规律的研究属于具体实际问题，需要建立可靠的模型，定性、定量地描述各层温度随时间变化的规律。通过分析已有的温度数据，找出假人外表皮温度与时间之间的数学关系，以此作为外热源在四层织物层间热量传递的平均热传导速率。再结合热学傅里叶定律，建立圆柱形非稳态导热模型，从而完善函数关系。基于此，定量得出各织物内表层温度随时间变化的数值，从而确定温度分布规律。

2.1 假人外表皮温度与时间的数学关系

将体温恒定为37 ℃的模拟假人放置在实验高温环境中，每间隔1 s，测量假人皮肤外侧的温度，并记录。利用MATLAB绘制出假人外表皮温度随时间变化过程趋势，如图1所示。

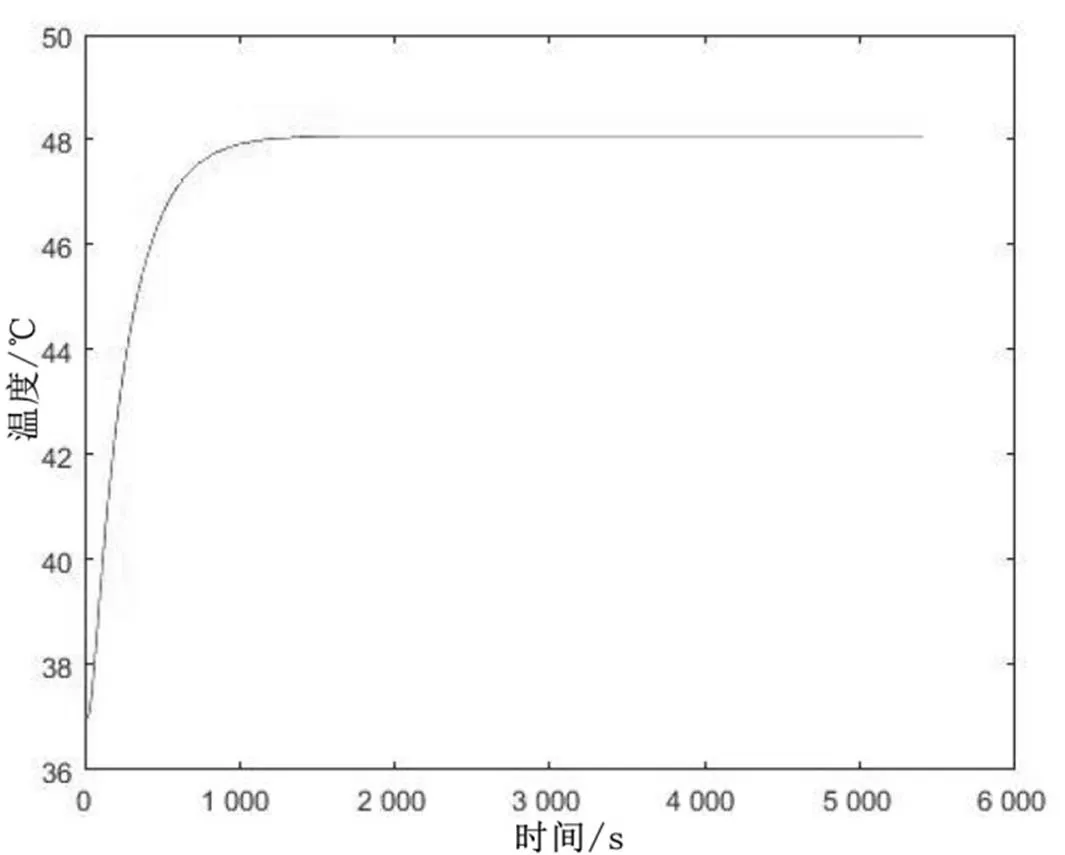
图1 假人外表皮温度随时间变化的趋势图

图1中，假人外表皮温度变化具有阶段性，前期逐渐增加，后期增加缓慢至不再发生变化。说明刚进入高温环境时，由于防护服内外温差大，热传递速率快，热量经过四层传至假人外表皮速率快，以致温度上升加快。随着时间的延续，相应层之间温差减小，导致热传导速率变小。最后温度不变，表明假人外表皮温度基本保持恒定，从而也说明防护服隔热效果达到极限值。

图1中，温度变化是热量经过四层之后到达假人外表皮引起的，由于时间间隔为单位时间，因而图1可以反映外热量经过四层介质后，单位时间内温度变化情况。假设热量在四层介质面中传导速率恒定，因此图1温度变化可以作为热量在四层介质中的平均热传导速率，记作Q。利用MATLAB对图1拟合成数学方程，以便对假人外表皮温度进行定量描述。由于温度变化具有阶段性，为减小误差，对其进行分段拟合。

最终得到热传导速率Q与时间之间的数学关系如下：

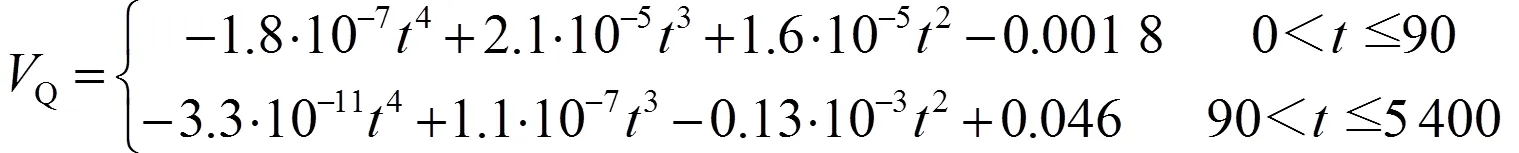
2.2 圆柱形非稳态导热模型的建立

假设假人身体结构为圆柱形，即防护服也呈圆柱形分布。在高温环境中，热量会沿着温度由高向低方向流动，即沿着Ⅰ、Ⅱ、Ⅲ到Ⅳ层传导过程，如图2所示（在图2中只取圆柱俯截面）。

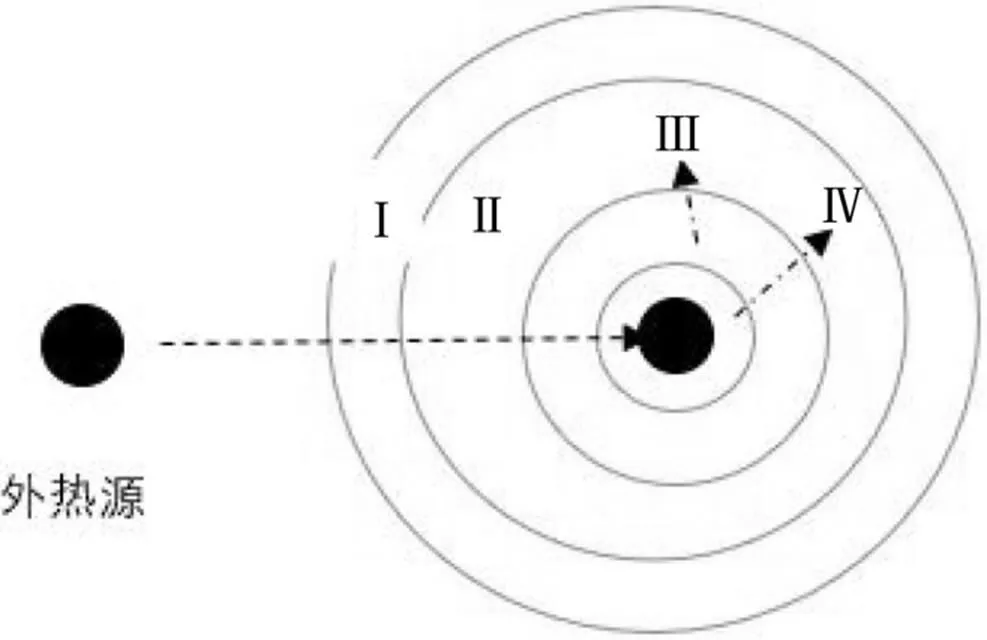
图2 圆柱形导热模型热量传导过程图

在《传热学》[10]中，任意方向上的热流密度矢量，可以分解为三个坐标方向的分量。同时与介质层热传导率、介质密度、比热容、物体内源生成热以及介质厚度有关。而且在圆柱坐标（，，）中满足关系：

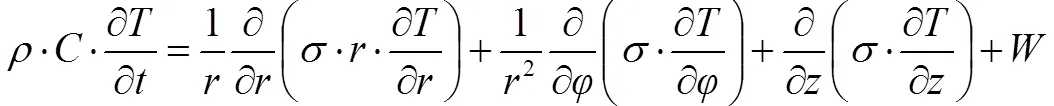
2.3 圆柱导热模型的求解过程

假设只通过一个内外半径分别为1，2的圆柱，其中内外表面分别维持均匀恒定的温度1，2。此外，假设假人各圆柱侧面受热均匀，所以，只考虑沿半径方向上的一维导热。因此，式（2）中对，的导数项为0。同时，假定假人在各时刻点处热量是稳定、平衡、均匀地传输，从而温度对时间的导数为0。对假人而言，本身热源维持恒定37 ℃，在各时刻点可视为不变。

综上所述，将公式（2）化简为：

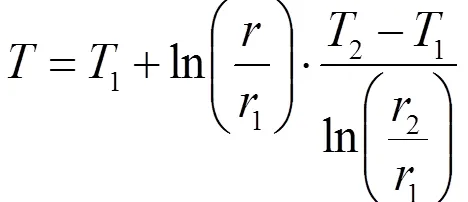
又由热学傅里叶定律[11]得：

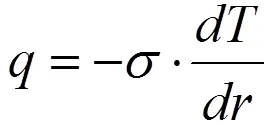
式（5）中：为热传导速率（=Q）；－（负号）表示热量向温度低的方向传递。将式（4）代入式（5）中，可得半径为2圆柱接触内表面温度2满足关系：

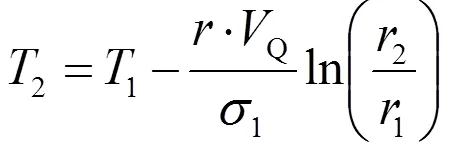
假设各介质层参数如表1所示。

表1 防护服各层参数值

分层密度ρ/（kg/m3）比热C/J/（kg·℃）热传导率σ/W/（m·℃)厚度r/mm Ⅰ3001 3770.0820.6 Ⅱ8622 1000.3706.0 Ⅲ74.21 7260.0453.6 Ⅳ1.181 0050.0285.0

结合式（1）和式（6）可求，到达Ⅱ层接触内表面温度2=72.670 1 ℃。同理，可求外热源热量传到其他各层接触内表面的温度，因此可以得到各层接触内表面温度随时间的变化规律，如表2所示。

表2 各层温度随时间变化规律

各层分布各层温度减少量/℃各层内表面最终温度/℃ Ⅰ内表层2.329 972.670 1 Ⅱ内表层16.048 256.621 9 Ⅲ内表层8.296 548.325 4 Ⅳ内表层0.120 948.204 5

2.4 温度分布规律的总结

由表2可知，外热量经过四层介质面到达假人表皮的温度随时间逐渐降低。在四层介质面中，Ⅱ和Ⅲ层是隔热的核心层，热量的阻隔主要是由这两层完成。其中，Ⅱ层相对Ⅲ层具有更大的优势，温度减少量为16.048 2 ℃。Ⅰ层和Ⅳ层是防护层，保护工作人员的安全。Ⅰ层是外防护层，主要负责隔离外热源，防止烧伤，也具有一定的隔热效果，温度降低2.33 ℃。Ⅳ属于内防护层，防止热源传至皮肤，造成烫伤，同时，也起到隔离其他层的作用，保护表皮。因此，一件高温专用服装主要在于中间层（Ⅱ、Ⅲ层）与Ⅳ层的设计。

3 建立双层线性规划模型对中间层与Ⅳ层最优厚度研究

3.1 研究思路

在四层介质中，Ⅰ层与外热源接触，隔离热源物质比隔热更重要。Ⅱ、Ⅲ是中间层，是阻隔热源的关键层，防护服隔热性能的优劣主要由中间Ⅱ、Ⅲ层决定。Ⅳ层属于隔热层与人体表皮层的间隙，对人体表皮具有保护作用。然而，一件优质的防护服既要做到更大限度隔热，同时也要尽可能保护人体表皮不受伤害。所以，研究中间层与Ⅳ层的最优厚度，具有重大实际作用。Ⅱ层与Ⅲ层都是主要隔热层，在性能上略有差异，但可将其“合参划一”，视为整体研究。

通过上述分析，研究中间层（Ⅱ、Ⅲ层）和Ⅳ的最优厚度是本文的核心。通过建立中间层、Ⅳ层厚度和热传导速率三者之间的双层非线性规划模型。再次利用“合参化一”思想，将中间层、Ⅳ层厚度统一为整体变量参数，从而研究整体变量与热传导速率之间的最优化问题。经过模型求解，可解得整体变量的取值范围。再建立中间层与Ⅳ层厚度两者之间的非线性规划模型。以整体变量参数的界定范围作为新的约束条件，结合假定模拟条件，完善约束条件；最后可以得出中间层和Ⅳ层最优厚度的关系。

3.2 双层非线性规划模型的建立

假定模拟条件：外界环境温度80 ℃，确保工作30 min时，假人皮肤外侧温度不超过47 ℃，且超过44 ℃的时间不超过5 min，其余参数保持表1中数值不变。

本文以外热源传至假人皮肤温度的最大值作为目标函数。在限定的时间内，若以最大热传导速率传递热量没有超过温度的极限值，则以低于最大传导速率传递热量，一定不会达到限定的温度极限。结合公式（6），可以确定目标函数：

假设中间Ⅱ、Ⅲ层厚度用2，3表示，Ⅳ层厚度用4表示，从而目标函数可变为：

根据已知条件，同理可得约束条件一：

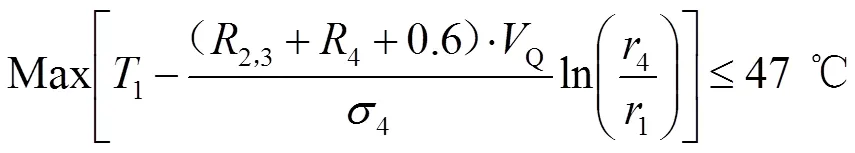
0 min＜≤30 min

由于假人皮肤层外侧温度一直呈上升趋势，因此只要保证在25 min内，假人皮肤外侧温度不超过44 ℃即可。从而可得约束条件2：

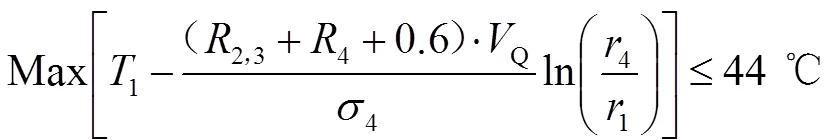
0 min＜≤25 min

由式（1）可知，当∈（0，25）时，解出热传导速率Q的范围0≤Q≤1。根据前人的研究经验，中间层和Ⅳ层都有一定的上限值，大致范围为：

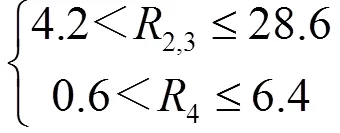
综上所述，最终建立中间层、Ⅳ层与热传导速率三者的单目标双层非线性规划模型：

从函数最值角度，进行最值的转化，代入1=80 ℃等数据并化简，可得三者的双层非线性规划模型：

3.3 双层非线性规划模型的求解

在式（7）中，目标函数含有三个变量参数，无法解出各自的最优解。因此，再次利用“合参划一”，将中间层与Ⅳ层看成整体变量，记作。从而可以得到整体变量与热传导速率Q之间的单目标非线性规划模型：

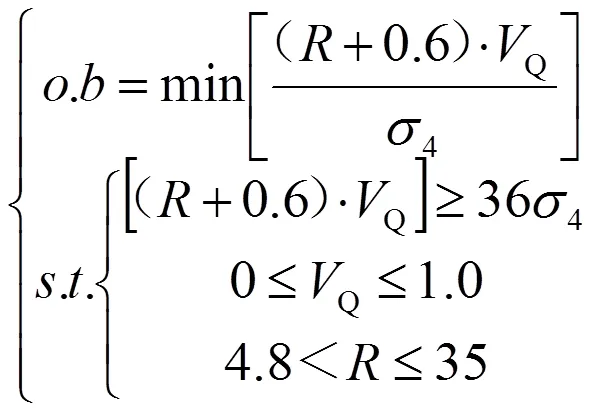
要求解式（8）目标函数的最小值，应使得热传导率最大，在四层中，Ⅱ层的热传导率最大。所以，取4=2。结合最优规划解[12]的条件，代入MATLAB可解得：

12.72≤（9）

结合式（7）和式（9）可确定中间层与Ⅳ层之间满足以下关系：

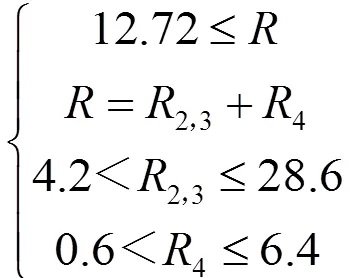
要建立中间层与Ⅳ两者间的非线性规划模型，需要建立新的目标函数，约束条件为式（10）。结合实际，防护服厚度与人体舒适度之间存在很大的关联[13]，高温防护服不适合长时间穿戴。所以，在满足国家防护服标准前提下，厚度越薄越好。从而转变求解参数的最小值。但是以两者厚度之和最小作为目标函数，与约束条件相重合，显然求解不出各自的最优解。同时，结合现有的条件，中间层与Ⅳ层都属于独立层，两者之间不存在物理相关性。所以，只能建立数学相关性。然而，在现有有限的条件下，数学相关性也难以确立，因此，建立新的目标函数具有很大的难度，但是并不代表本文模型建立是失败的。从式（10）可以确定中间层与Ⅳ之间满足相互关系的可行域范围，该范围可以说明，中间层与Ⅳ层具有一定的取值范围，围绕区间范围的不同厚度取值，可以为防护服实际模拟、设计提供数值参考。

4 结语

在高温作业服装方面的研究已经具有比较完善的理论，但本文嵌套式双层规划思想的提出是新颖的。而本文合参划一思想的提出，也具有新的特点。将各织物层看成统一整体，逐一分化整体，从另一角度诠释防护服设计的理论依据。此外，本文所建立的模型较为“理想化”，求解得出结果并不精准。但是，模型的建立考虑主要影响因子，结果不失一般性。尤其解出中间层（Ⅱ、Ⅲ层）和Ⅳ层厚度的范围，可以为高温作业服装的设计提供数值参考，具有一定的现实意义。

［1］赵海英，张美辨，邹华，等.高温作业对人体行为功能的影响［J］.浙江预防医学，2007，19（10）：36-37.

［2］李宁舟，郝欧亚，汪宪宏，等.高温作业服装材料厚度的设计［J］.新型工业化，2018，8（10）：95-97.

［3］李俊豪.基于差分法的高温作业专用服装设计［J］.科技与创新，2019（11）：116-117，120.

［4］方志法，李浩铭，王文昊.高温作业专用服装的多层非稳态热传递模型的研究［J］.价值工程，2019（18）：260-262.

［5］易静姝.高温作业专用服装的设计与研究［J］.科技创新与应用，2019（11）：82-83.

［6］徐亮，朱家明，李丹，等.基于改进傅里叶变换对热防服的优化设计［J］.齐齐哈尔大学学报（自然科学版），2019，35（2）：54-59.

［7］张文远，朱家明，张文蔚.基于热传导机理的高温作业专用服装优化研究［J］.辽宁工业大学学报（自然科学版），2019，29（2）：111-116.

［8］毛瑶瑶，朱家明.基于热传导及遗传算法对防热服的优化设计［J］.兰州文理学院学报（自然科学版），2019，33（3）：26-30.

［9］张泽群，李宏，刘毅，等.基于热传导学和有限差分法的高温专业服装设计［J］.新型工业化，2018（10）：95-97.

［10］杨世铭，陶文铨.热力学［M］.北京：高等教育出版社，2006.

［11］杨恒熹.关于傅立叶定律的表述［J］.益阳师专学报，1988，32（2）：79-81.

［12］李岸巍，阮豫红.线性规划模型解的判定［J］.山西师范大学学报（自然科学版），2003，17（2）：94-96.

［13］吕石磊.极端热环境下人体热耐受力研究［D］.天津：天津大学，2006.

TS941.2

A

10.15913/j.cnki.kjycx.2019.15.008

2095－6835（2019）15－0022－04

姚吉（1997—），江西吉安人，就读于河北工程大学，本科。金冰慧（1998—），女，河北工程大学本科生，研究方向为通信工程。邢曜琛（1998—），男，河北工程大学本科生，研究方向为通信工程。

〔编辑：严丽琴〕