定远县池河大桥桥址水位分析计算
任恒学,张晓娟
(安徽省淠史杭灌区管理总局工程处,安徽 六安 237010)
1 工程概况
拟建池河大桥位于滁州市定远县池河镇红心沛村附近,距离上游七里河口1.50 km,距离下游池河闸3.28 km,桥址以上流域面积2 494 km2。桥长406 m,桥跨布置为1 625 m,桥梁宽度25.5 m,上部结构采用25 m标准跨径预应力混凝土小箱梁,下部结构采用桩柱式桥墩,肋板台,墩台采用钻孔灌注桩基础。拟建桥梁与河道正交,桥墩轴线与水流方向基本平行。
图1 为工程河段水系图。

图1 工程河段水系图
2 水位分析计算
因桥址处缺乏实测水文资料,现需推求桥址处设计防洪标准水位。根据《安徽省池河治理工程初步设计报告》[1],池河大桥桥址处流量成果见表1所列。

表1 池河大桥桥址处流量成果表
该工程利用能量方程和曼宁公式及桥址处上游石角桥,下游光明水位站测站水位流量关系曲线进行插值计算,三种方法进行推求。
2.1 能量方程方法
利用池河大桥桥址处下游池河闸堰水位作为控制水位,利用能量方程,见式(1),以100 m一个断面进行推求。

式中:Z1、Z2为河道底高程;Y1、Y2为河道断面水深;V1、V2为计算段上、下游断面平均流速;a1、a2为计算段上、下游断面的动能修正系数;hf为沿程水头损失;hj为局部水头损失。
计算成果见表2所列。

表2 能量方程方法计算成果表
2.2 曼宁公式计算方法
利用现状地形断面,按明渠均匀流曼宁公式,见式(2)进行计算。

式中:A为断面面积;n为河床糙率(经计算取值为0.04);i为水面比降(近似取河床比降0.143%);R为水力半径。计算成果见表3所列。

表3 曼宁公式计算方法计算成果表
2.3 插值法
根据《安徽省池河治理工程初步设计报告》,上游石角桥站及下游光明站水位流量关系曲线进行桥址处水位插值计算,石角桥站及光明站水位流量关系曲线见图2和图3所示。

图2 石角桥水位流量关系曲线图

图3 光明站水位流量关系曲线图
根据上述水位流量关系拟合曲线,以及20 a和100 a一遇设计流量,可知石角桥和光明站20 a一遇、100 a一遇设计水位。假设桥址处与石角桥和光明站之间水面比降在发生20 a一遇设计洪水和100 a一遇设计洪水时变化不大,由上、下水位内插可知桥址处20 a一遇及100 a一遇洪水设计水位。计算成果见表4所列。

表4 插值计算方法计算成果表
能量方程、曼宁公式计算方法及插值计算方法成果对比见表5所列。
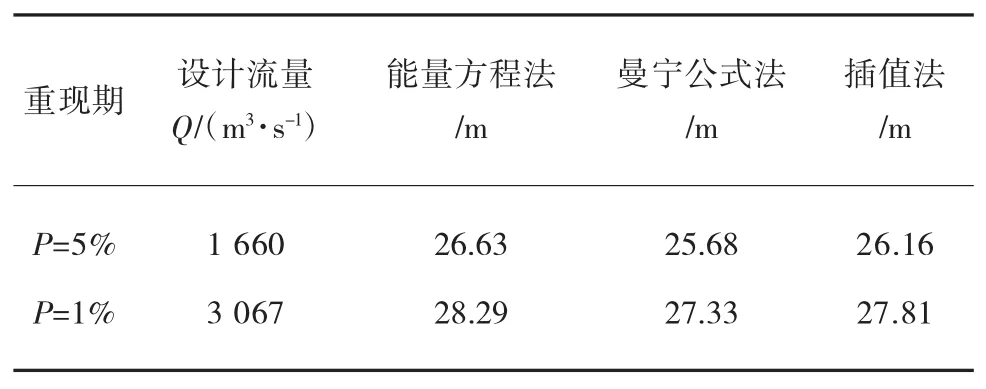
表5 成果对比表
2.4 水文计算成果分析
曼宁公式适用于明渠恒定均匀流,而实际天然河道地形地质条件复杂且不均一,多处于非均匀流态,曼宁公式中参数取值对计算成果影响较大,如该工程利用曼宁公式计算出桥址处水位27.33 m(设计流量Q=3 067 m3/s),却低于下游池河闸处水位27.90 m(设计流量Q=3 067 m3/s),计算成果不合理。
因石角桥站和光明站距离桥址较远,池河上、下游坡降变化较大,线性插值精度无法满足设计精度要求。
结合《安徽省池河治理工程初步设计报告》中七里河口水位计算成果,依据池河闸堰上水位作为控制水位,并运用能量方程推求池河大桥处水位,更符合实际情况[2-3]。
3 结论
根据该工程,利用池河大桥下游池河闸堰上水位作为控制水位,并运用能量方程逐个断面往上游推算计算成果,更符合天然河道实际情况。在天然河道水面线中,运用曼宁公式,难以把控参数取值,误差较大。天然河道坡降较均一且距桥址较近时,可运用插值法。

