农产品价格B-N分解与随机冲击的惯性研究
张 超,侯 凯
(1.安徽财经大学 金融学院,安徽 蚌埠 233030; 2.山东交通学院威海分校 国际商学院,山东 威海 264200)
内容提要:农业是百业之本、粮价是百价之基,农产品价格波动对社会生产和居民生活都具有广泛影响。为弥补已有相关研究方法的不足,本文从解析农产品价格波动的经济涵义入手,运用B-N技术分解我国主要农产品价格波动中的持久性成分和暂时性成分,并考察农产品价格随机冲击的惯性,以刻画我国农产品价格的动态特征,以期提高微观主体对农产品价格趋势变化的预判能力,进而更好安排消费、生产及经营等活动,同时为政策调整提供科学信息,减少社会福利损失。
农产品作为基本的生活必需品,对居民生活及社会生产存在直接或间接的影响。2013年以来,我国粮食市场进入了新的供求周期,由曾经的供求偏紧转向宽松并出现连续三年供大于求,加之国内外价格倒挂,开始出现了“高库存、高进口、高成本”等供需错配的情况。虽然自“十三五”开局的2016年开始,国内粮食再获丰收,但结构性矛盾却依然存在。随着国家粮食政策收储范围的缩小,粮食价格支持政策改革的步伐加速,玉米价格已经开始由市场形成,粮食价格似乎存在向下波动的走势①。
与粮食价格波动趋势形成对比的是猪肉价格。猪肉作为我国居民最主要的肉食来源,国内生猪存栏量早已居于世界首位。受猪周期的影响,国内生猪价格呈现出一定的规律性变动②。事实上,自20世纪90年代以来,除了2000-2003年猪肉价格相对稳定之外,我国猪肉价格处于波动的上涨态势。特别是2003年“非典”疫情之后,国内猪肉价格更是出现了频繁暴涨暴跌的波动。例如,2016年上半年猪肉价格不断上升,最高时(5月)达到21元/公斤,而此后却开始一直回落至11月;进入2017年,猪肉价格呈现出先跌后涨走势。随着环保力度的不断加大,猪肉进口政策的逐步开放,加之不可预知的疫病等影响因素,猪肉价格波动并没有因为规模化生产而消失。
在粮食和猪肉价格波动的影响下,国内农产品价格波动可能会加剧,进而影响一般价格水平。同时,由于农产品在价格链“终端”属于最终消费品,价格链“始端”则属于生产要素。农产品价格的率先波动将带来相关商品价格波动的连锁反应,不可避免产生价格联动效应。因此,农产品价格波动不仅仅是物价水平的最终表现形式,更加重要的是将对通胀或通缩做出重要的结构性“贡献”。
从农产品供求关系角度分析价格波动是惯用的研究路径。改革开放以来,我国发生了几次较为严重的通货膨胀,每次都伴随着主要农产品价格的大幅上涨,因而农产品价格波动的传导性成为社会各界关注的重点。虽然已有文献对农产品价格变动的原因做了比较全面的研究,但并没有对各种影响因素的持久性做进一步分析,特别是没有细分价格变动中的“持久性因素”和“暂时性因素”,因此就难以分辨其波动是短期异动还是长期趋势,有可能过度放大对通胀或通缩预期产生的“示范”效应,而不准确的预期最终可能通过微观主体的行为得以自我实现(即Self-fulfillment expectation),从而给经济发展带来巨大的社会成本和福利损失。
一、农产品价格波动的经济涵义解析
在各种推动农产品价格波动的可能因素中,既包括主导农产品价格走势的持久性因素,也包括引发异常波动的暂时性因素。其中,经济发展趋势、农业供给侧改革及环保政策趋紧等因素是具有系统性特征的持久性因素。首先在经济新常态下,经济增速放缓,经济增长由高速度向高质量转变,对农产品供给的层次提出了更高的要求,即调整农产品结构,提供绿色优质的农产品。其次,农业供给侧改革对粮食高库存提出了新要求,粮食等重要农产品价格形成机制和收储制度亟待改革。再次,环保政策的趋紧,要求必须转变传统粗放的农业发展方式,粮食生产要转向科技效益,生猪生产也正朝着规模化和科学化方向发展,“大鱼吃小鱼”的兼并模式也将持续较长时间。最后,中国已经越过刘易斯拐点,人口红利也将消失,劳动力正由相对过剩向相对短缺转变,加之土地承包经营权政策和户籍制度的改变,农业劳动力成本将不断上涨。一方面这些因素驱动农产品价格形成确定性或随机趋势,推动农产品价格重新找到均衡价格;另一方面这些因素通过持久性冲击将逐步“固化”于农产品价格形成机制中。
暂时性因素则包括(非毁灭性的)自然灾害、动植物疫情病情、国内外资本投机、流动性过剩或短缺等。这些影响因素作用比较明显,作用机理也已经得到了充分的研究。
综上,农产品价格波动主要源于两方面冲击,一是经济发展趋势、农业供给侧结构性改革等持久性因素;二是自然灾害、国际游资及流动性过剩或短缺等暂时性因素,尤其是后者往往造成农产品价格的非理性波动。为此,我们提出以下三个问题:一是既然农产品价格波动主要源自两方面冲击,那么如何合理地分解出价格变动中的持久性成分和暂时性成分?二是如何准确地度量随机冲击,特别是其中的暂时性成分对农产品价格的影响?三是在经历了频繁的随机冲击之后,农产品价格是否已经形成了持续的价格波动路径?这三个问题的解答,不仅有助于微观主体准确把握农产品价格波动以提高其对价格趋势的预判能力,而且还能为政策当局有效管理通胀或通缩预期及实现经济平稳发展提供参考。
二、研究设计
(一)分解技术的选择
如何将农产品价格序列中的确定性及随机性趋势成分分离出来,并将剩余的平稳部分作为周期波动成分,进而分析农产品短期波动的特征,这不仅是一个经济问题,还是一个技术难题。按照处理时间序列方式的不同,目前已有的周期估计方法可分为两大类,一是时域(time domain)分析,二是频域(frequency domain)分析。
早期的线性趋势分解方法与一阶差分法,以及多变量分析中的结构式向量自回归(即SVAR)方法,都可归类为时域分析方法,即直接分析数据随时间变化的结构特征。线性趋势分解方法、一阶差分法虽然操作简单但需要假设原有序列仅有随机性趋势;SVAR方法以先验经济理论为基础,虽有较强经济学涵义,但对数据和样本的要求相对较高,在非大样本数据条件下的实用性不强。而B-N分解方法对以上问题的处理相对来说具有更强的优势。B-N分解的思想源自Beveridge and Nelson(1981)[1]提出的Beveridge-Nelson分解公式,他们从理论上证明了具有单整(I(1))特征的序列数据可分解为时间趋势、随机游走、平稳过程和初始条件之和。其中,持久性成分包含有确定性趋势与随机游走所表述的随机趋势。而短期成分即分解公式中的平稳过程,也被称为“周期性”成分。
估计周期的实践中用到各种滤波方法则属于频域分析,即把时间序列看成由多个不同频率的规则波(如正弦波或余弦波)迭加而成。研究经济周期时广泛使用的滤波方法有HP滤波、BK滤波。其中,HP滤波法在求取趋势成分时,先验的假设趋势成分为充分平滑的曲线,因而滤出的短期成分波动会较大,故存在“虚假周期”(spurious cyclical behavior)之嫌,这也是HP方法招致诟病的重要原因。BK滤波法是基于理想带通(Ideal Band-Pass)滤波的“线性近似(逼近)”,同样也会遭遇这一问题。另外,HP滤波得到周期由于包含有随机趋势将导致冲击的持久效应被过度估计(over-estimated),这显然违背了本文的初衷,而B-N分解方法能有效回避上述这些问题,这构成了本文选择B-N分解法的重要理由。
在B-N分解中,由于确定趋势和周期的理论解析式中出现了“无穷大”,因此运算过程比较繁琐③。不过,Newbold (1990)[3]依据Wold定理简化和精确了运算过程:任意协方差平稳过程必能表述为ARMA过程,而任何一个ARMA过程又可表述写为MA()过程。因此,Newbold(1990)基于ARIMA(p,1,q)表达式,将B-N周期表述如下:
(1)
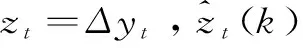
在趋势周期的技术框架下,趋势成分永远存留于水平条件期望之中,通过累积使无限远期的水平条件期望形成趋势成分,而周期成分由于仅具有短期效应而不出现在无限远期的水平条件期望中[4]。这暗示趋势成分受到冲击后,会发生永久性的改变,而周期成分受到冲击后,仅会发生暂时性的偏离。
趋势成分对应着持久性冲击,而周期成分对应着暂时性冲击。因此,运用科学的时序技术对我国农产品价格序列进行趋势周期分解,有助于识别出持久性冲击和暂时性冲击对价格序列的影响。也即是说,根据周期形态刻画农产品价格波动的持久性特征,可以进一步分析随机冲击对我国农产品价格波动的影响程度。
(二)惯性的测度
由现代时间序列理论可知,使用AR模型中滞后项的系数和可以度量随机冲击的持久效应。参考经典文献(Taylor,2000;Willis,2003)[5-6],本文模型设定如下:
yt=c+α(L)yt-1+ut
(2)
其中,yt-1代表B-N周期,也即短期波动;ut表示仅具有短期效应的随机冲击;α(L)=α1+α2L+…+anLn-1代表滞后算子多项式;c为常数项。
“惯性”的实质是在短期波动过程中一个单位的随机冲击带来的累进效应[7-8],可以使用累积脉冲反应函数(CIRF) 进行刻画,即:
(3)
结合等式(2)和(3),可以将CIRF解析表达式改写为如下形式:
(4)
不难看出,α(1)越接近于1,累积脉冲反应函数的值越高,反之越低。因此,α(1)=α1+α2+…+an可以衡量短期波动惯性的指标。
考虑到滞后项之间可能存在的共线性,如果直接对(2)进行回归,可能会影响系数估计的精确度。因此,我们可以根据AR模型的ADF检验表达式的转化思路,将原有AR模型重新写成如下形式:
(5)
等式(5)中Δ表示一阶差分算子,系数ρ与(2)中α(1)相等,即为惯性系数。
(三)估计方法
即便模型设定正确无误,使用经典OLS方法对ρ的点估计仍然是统计有偏的,并且ρ值越接近1时,偏差会更为显著。此外,区间估计与假设检验所依赖的渐近法则(中心极限定理与大数定理)失效。渐近法则在ρ∈(0,1)内并不一致成立,随着ρ越接近1中心极限定理的收敛速度减缓;ρ等于1,中心极限定理不再适用。实际上,ut的分布也将影响统计推断,ut的分布通常未知,可能较大地偏离了正态分布,这意味着以标准的正态近似方法无法构筑出准确的置信区间。
Andrews and Chen(1994)[9]在早期研究中曾尝试解决这一问题,但均以中央极限定理为基础对扰动项施加了正态性假设。针对此问题,Hansen(1999)[10]在前期研究的基础上,引入bootstrap方法以避免事先确定误差项先验分布的局限性。具体来说,我们可以使用蒙特卡洛方法模拟出最小二乘估计的极限分布,并利用格点搜索法(grid search)来修正ρ值及置信区间,解决OLS方法的统计偏差问题。因此,本文使用Hansen(1999)的Grid-Bootstrap方法来修正惯性系数的估计。为了确保估计结果的可靠性,同时构筑grid-t与grid-α统计量,进而估计出这两个统计量的Bootstrap分位数函数。
Grid-t统计量的中值无偏估计量定义为:
(6)
grid-α统计量的中值无偏估计量定义为:
(7)
(8)
(9)

(10)
(11)
三、实证分析
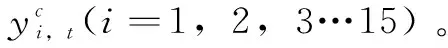
建立在ARIMA估计基础之上的B-N分解法,需要事先确定价格序列的ARIMA过程阶数。通常认为,如果随机时序轨迹的真实数据生成过程含有MA成分,其部分自相关函数(PACF:Partial Autocorrelation Function)应该呈现拖尾特征,而自相关函数(ACF:Autocorrelation Function)应该出现衰减特征。AR过程对应的是截尾的PACF和衰减的ACF。据此准则并结合信息准则确定ARIMA过程的最优阶数组合,ARIMA模型参数估计采用ML法,迭代过程使用Gauss-Newton算法。限于篇幅,此处没有报告具体的定阶过程。

图1 农产品价格中周期成分变化轨迹
图1刻画了15种农产品价格中周期成分的变化轨迹,时序图包含了相当丰富的信息。概括地说,自2004年6月以来,15种农产品价格无一例外地出现过较大幅度的波动。如2007年到2008年,猪肉价格的上涨尤为突出,小麦等粮食作物价格波动明显,总体处于上升阶段。受金融危机影响,2008年末农产品价格出现短暂回落,但随后又迎来了新一轮上涨。此轮上涨的主要是仔猪、猪肉、棉花、玉米及大豆,小麦等粮食作物并未充当农产品价格上涨的主导因素。受异常天气的影响,2010年到2011年的粮食作物价格跌宕起伏,波动较为剧烈。进入2012年后,粮食价格涨幅趋缓,大豆价格趋稳,但玉米和生猪等农产品价格仍在频繁波动。
我们进一步采用Grid-Bootstrap方法对价格波动的惯性系数进行无偏估计。在估计过程中,设定格点数为100,boot次数为1999。结果汇报在表1中。结果显示,基于grid-t与grid-α的估计结果基本是一致的。具有统计无偏性的中值无偏估计量均小于单位1,说明遭受随机冲击之后,农产品价格波动均呈现出“均值回复”的特征。因此,暂时性冲击的特征及影响路径得以有效识别。然而,不同农产品价格均值恢复速度有所差异。其中,籼稻、大豆、棉花、猪肉具有高惯性系数,均超过了0.9,90%置信区间上界均超过1,这意味着经典计量方法对于这些惯性系数的统计推断将会产生较大的偏倚。同时,这也表明受到随机冲击后,恢复到均衡价格需要较长的时间。具体来看,高惯性的农产品主要是粮食作物及猪肉。

表1 农产品价格波动惯性的Grid-Bootstrap估计
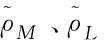
四、敏感性检验
农产品价格周期表现出的深远变化,这促使我们思考其惯性特征是否也随之发生了变化。如果短期价格波动的惯性发生了结构性突变,那么忽略这种突变情况下估计出的惯性系数则是向上偏倚的。Perron and Vogelsang(1992)[11]指出,固定参数模型可能错误地把结构性突变识别为随机冲击衰减速度减缓,从而高估随机冲击的惯性,因此剔除结构突变因素后惯性将会相对较低。
在此,我们将借鉴Andrews and Ploberger(1994)[12]的未知断点检验方法对惯性系数的稳定性进行检验。这一检验依然依托传统的Chow检验[13]。只不过,需要先设定一个搜索域τ,然后在该域内所有点上进行Chow断点检验,从而得到对应的一系列Wald检验统计量,Andrews(1993)[14]正是基于这些Wald检验统计量设计出supW统计量,即:
supW=supW(τ)|τ∈[τmin,τmax]
(12)

表2 敏感性检验
如果supW具有统计显著性,则对应的时刻即是惯性系数发生结构性变化的断点日期[7-8]。而后Andrews and Ploberger(1994)构造了两个类似的统计量:ExpW与AveW。相比supW,这两个统计量具有更好的统计性质。但二者适用范围稍有差异,Andrews et al.(1996)[15]模拟比较发现,AveW适用于小的结构变迁而ExpW适合大的结构变迁。它们分别由如下方式计算得到:
(13)
(14)
其中,k表示搜索域内Wald统计量的个数。
需要指出的是,结构突变点是扰动系数,其原因是它只存在于备择假设之中。因此上述统计量的分布并不是标准的,Andrews(1993)、Andrews and Ploberger (1994)模拟了统计量渐近分布的临界值,Hansen(1997)则进一步计算这些统计量对应的渐近概率值。本文尝试进行结构性检验,设置的搜索域为全样本中间70%区间。表2的检验结果说明不存在结构变迁,即农产品价格波动的惯性Grid-Bootstrap估计结论具有稳定性。
五、主要结论
首先,本文选择了更合适的价格序列分解技术,科学分解农产品价格波动中的持久性成分和暂时性成分,并通过暂时性成分更好地识别农产品非理性波动的成因。通过对常用时域和频域周期分解模式的研究,发现B-N分解技术传承了时域分析的思想,但相比于早期单变量简易分解方法与多变量结构分解法,该分解方法具有更强的优势。同时,B-N分解技术亦能有效回避HP滤波和BK滤波等方法中存在的“虚假传导”等问题。而针对B-N分解运算过程相对繁琐的弊端,学者们也进行了有益的改进,有效降低了运算成本。因此,本文选择运用B-N分解方法,对代表性农产品价格序列中的持久性成分和暂时性成分进行了科学分解。根据农产品价格中暂时性成分的变化轨迹来看,自2004年6月以来,15种农产品价格都出现了较为显著的波动。
其次,本文构建了一种更稳健的惯性度量模型,估计随机冲击对主要农产品价格波动的惯性,以期准确捕捉粮食等主要农产品价格波动的特征。伴随单位根模型的发展,目前国际上主流文献的做法是运用自回归模型中的滞后因子系数的算术和,来度量随机的暂时性冲击对价格波动产生的持久效应。鉴于经典计量方法在统计推断中的严重偏倚,我们借助了Hansen(1999)的Grid-Bootstrap技术,同时构建grid-t与grid-α统计量对农产品短期波动的惯性系数进行严谨的统计推断,得到了较为一致的结果。也即是说,在受到金融危机和异常天气等随机冲击之后,这些农产品价格波动都具有“均值回复”的路径特征,但不同惯性系数的农产品在遭受随机冲击后,恢复到均衡价格的速度有所差异。
最后,考虑到农产品短期波动率的惯性可能发生结构性改变,同时注意到,如果借助已有先验信息确定的已知时点作为样本分割点来考察农产品短期波动率的惯性变化,可能难以精确捕捉其真实的变动情况。因此,本文应用Andrews(1993)等提出的未知断点结构稳定性检验法,对惯性系数的变化进行了考察,以减少由于断点的任意选取而对惯性系数估计带来的敏感性。检验结果说明农产品价格波动的惯性估计结论具有稳定性。
注释:
① 国家按照“市场定价、价补分离”的原则对玉米收储制度进行改革,将玉米临时收储政策调整为“市场化收购”加“补贴”的新机制,玉米价格由市场形成。市场价格反映供求关系、调节生产和需求,生产者随行就市出售玉米,各类市场主体自主入市收购。
② 即生猪供应短缺-生猪价格上涨-增加能繁母猪数量-生猪供应过剩-生猪价格下跌-减少能繁母猪数量-生猪供应短缺……。
③ 为了降低运算成本,Cuddington and Winters(1988)[2]等在文献中讨论了一些解决方案。

