对称性及其在解题中的应用

王建忠

(江苏省启东中学 江苏 南通 226200)

对称是一个常用词，现代汉语词典的解释是指图形或物体对某个点、直线或平面而言，在大小、形状和排列上具有一一对应关系．数学家外尔教授给出了对称性的一个极好的定义，意思是如有一件东西，你有可能对它做某种操作，使得你完成了操作之后，它看起来同操作以前是一样的，那么那件东西就是对称的[1]．这里说的对称主要表现在空间形式上，对称还可以表现在时间过程中，对称性是自然界的普遍规律，对称性方法和对称性原理的广泛应用，使物理学取得了许多令人振奋的成果．库仑利用对称分析的思想确立了库仑定律．在验证静电力与电荷量成正比时，当时人们只知道物体有没有电荷，但没有办法精确地测定物体所带的电荷量．为了寻找静电力与电荷量间的关系，库仑用了一个虽不够严格但极为巧妙的方法．他从对称性的物理思想出发，令一个带电金属球与半径、材料相同的另一个不带电金属球接触后分开，每球的电荷量应为原带电球的电荷量的一半，库仑就用这种对称均分的方法验证了静电力与电荷量成正比的规律[2]．对称守恒观是物理学科形成的认识自然界的基本思想方法和处理问题的基本思维方式．

本文从研究对象、物理过程、物理量3个方面讨论对称性在物理解题中的应用．

1 研究对象的对称

【例1】图1所示的网状电路中含有4个六边形，已知六边形每边的电阻都是r，求A，H间的电阻．

图1 含有4个六边形的网状电路

解法1：等势点短接法．等势点间无电流，可视问题的需要将其做短路或断路处理．

设想将A，H两端接入电源，由于电路关于过ACFH的直线对称，所以，各对称电路段上分布的电流应相等.因此，B，D为等势点；同理E，G也为等势点，可以将等势点短路，电路等效为图2(b)所示．

图2 图1的等效电路

这样A,H间的电阻可以看成A和B，B和E，E和H3个部分串联而成．B，E间是3部分并联，可求得

所以

解法2：对称轴折叠法．电路以ACFH为轴上下对称，沿ACFH对称轴对折，两电阻重叠，即为两电阻并联，得到如图3所示等效电路．易得

图3 对称折叠的等效电路图

点评：通过对研究对象(电路)的对称性分析，确定解题的总体思路或入手方向，作必要的等效处理，变复杂电路为简单电路．对称性既是一个理论概念，也是人们思考和解决问题的一种方法，对称性在物理学中有着举足轻重的作用，合理地使用对称性方法可使复杂问题简单化．

【例2】一玻璃齿轮，每个齿均为相同的正三角棱镜(顶角为60°)，若此装置能使光绕着齿轮转，求齿数为N时，玻璃的折射率n为多少? 当N=6时，折射率n为多少?

解析：当光绕着齿轮转时，由对称分析可知，光线在每个棱镜中的偏转情况必须是相同的，光路一定是对称的，在棱镜中的光线一定与棱镜底边平行，如图4所示．

由折射定律

得

当N=6时

点评：解题的第一步是选取研究的对象．通过审题，由结构对称分析出光路对称；经过科学推理，得出每个棱镜对光线的偏转情况相同，棱镜中光线平行于底边是解题的关键．对称分析是我们解决问题的一把钥匙，通过定性和定量两个角度对问题进行科学推理，找出规律，形成结论.

2 物理过程的对称性

物理过程对称又分时间对称和空间对称．

【例3】从地面上同一点以相同初速度v0=30 m/s先后竖直向上抛出2个小球，两小球抛出的时间间隔Δt=2 s，问第二个小抛出后多久与第一个小球在空中相遇？取重力加速度g=10 m/s2．

解法1：利用上抛运动规律求解．两个小球以相同的初速度上抛，不可能在第一个小球的上升过程中两球相遇，只能在第一个小球的下落过程中两球相遇．设第二个小球抛出后ts两球在空中相遇，此时先抛出的小球运动了(t+2) s．以抛出点为原点，竖直向上为y轴正方向，由上抛运动规律

相遇的条件是

y1=y2

联立得

t=2 s

解法2：利用上抛运动“上升过程和下落过程经过同一高度处的速度等大反向”这一空间对称性求解．相遇时有

v2=-v1

即

v0-gt=-[v0-g(t+Δt)]

30-10t=-[30-10(t+2)]

得

t=2 s

对第二个小球

v=v0-gt10=30-10t

得

t=2 s

图5 两小球的位移-时间图像

点评：利用对称性进行思考，得到了多种简洁的解题方法．在分析处理问题时，有意识地利用对称性，并使思维过程与之相适应，不但可以更好地把握问题的本质，还可以使思维和推理过程更简洁，更快地打开思路，并能快捷地解决问题，达到事半功倍的效果．

【例4】如图6所示由细杆组成的轨道，MN,CD两部分处于水平位置，长度均为L，两杆间距离为h．MEC是直径为h的半圆，与MN,CD在同一竖直平面内，且MN,CD恰为半圆弧在M,C两点处的切线．质量为m，带正电荷q的小球P，穿在细杆上，已知小球P与两水平细杆间的动摩擦因数为μ，小球P与半圆轨道MEC之间的摩擦不计，小球P带的电荷量不变．在MD,NC连线的交点O处固定一电荷量为Q的负点电荷，使小球P从D端出发沿杆滑动，滑到N点时速度恰好为零．求小球P从D端出发时的初速度v0．过程中小球所受库仑力始终小于重力．

图6 细杆组成的轨道示意图

解析：小球P从D端滑到N端全过程，由动能定理

式中Wf,WE,WG分别为摩擦力、电场力和重力对小球P做的功．由对称性可知，D,N两点是-Q电场的等势点，WE=0；WG=-mgh．要求出初速度v0，关键是求出摩擦力对小球P做的功Wf．由于电场力是变力，小球在水平杆上运动时，小球对杆的正压力是变力，因此滑动摩擦力是变力．但由于装置具有对称性，我们可以取DC,MN上关于O对称的两点P1,P2，设∠P2P1C=θ，如图7所示．

图7 例6解析图

小球P在P1,P2位置时，O点处电荷-Q对小球P的静电力大小相等，设为F，在P1,P2位置考察一微小位移Δs，摩擦力做功分别为ΔWf1,ΔWf2,有

ΔWf1=-f1Δs=-μN1Δs=-μ(mg-Fsinθ)Δs

ΔWf2=-f2Δs=-μN2Δs=-μ(mg+Fsinθ)Δs

这两个微小位移上摩擦力做的总功为

ΔWf=ΔWf1+ΔWf2=-2μmgΔs

DC,MN上位移可分成这样一对一对对称的微元，全过程摩擦力做的功为

Wf=∑ΔWf=-2μmg∑Δs=-2μmgL

将Wf,WE代入动能定理表达式，可得

点评：通过选取一对对称的过程微元，解决了滑动摩擦力变力做功问题．对称性是美的化身，物理学中对称美是普遍存在的，她可以是显性的，也可以是隐性的．我们不仅要懂得去欣赏她，更要有意识地去发现和利用她．

3 物理量的对称

【例5】测量空间某固定点的电场强度大小随时间的变化，得到如图8所示图线．电场是由两个相同的点电荷产生的，其中一个点电荷不动且到观察点的距离为d，另一个点电荷以恒定速度运动．求：

(1)每个点电荷的电荷量；

(2)运动点电荷到观察点的最近距离；

(3)运动点电荷的速度．

图8 例5题图

解析：当时间t很长时，运动点电荷与观察点相距很远，可以认为观察点的电场仅由固定的点电荷产生，这时场强为E0．设点电荷的电荷量为Q，则

该电荷可正可负．

从图8看出，t=0时，观察点场强为零．此外图像关于纵轴对称，又由于是两个相同点电荷产生的电场，因此，只有这样才可能，t=0时两点电荷与观察点在一直线上且关于观察点对称，运动点电荷与观察点相距d，这是运动点电荷与观察点的最近距离．运动点电荷的速度方向与固定点电荷和观察点的连线垂直(这样才能使场强E关于纵轴对称)．如图9所示，为求运动点电荷的速度，考察t=0时刻附近极短时间Δt，设点电荷是正电荷，Δt时间内观察点P点的场强由零增加到E，在等腰 ΔE0EP中

得

由此得

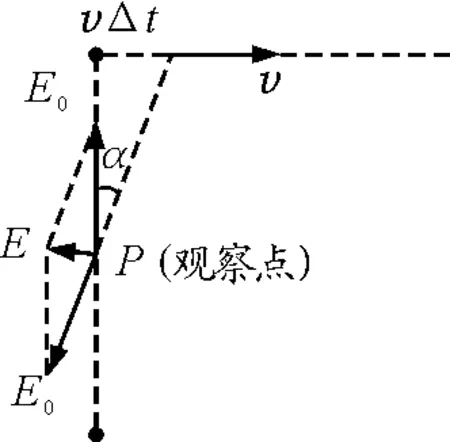
图9 例5解析图

点评：充分利用对称性的思想方法，可以提高直觉思维能力和形象思维能力，能很容易概括出我们所面对问题的关键，从而有效解决问题．

杨振宁先生说：“物理学最重要的部分是与物理思想有关的，绝大部分物理学是从物理思想来的，物理思想是物理学的根源．”[3]对称性是物理学的一个重要思想．在中学物理中，对称思想的应用不仅在于方便解题，提高分析问题、解决问题的能力，更重要的是可有效激发学生学习物理的兴趣，加深对物理规律、科学本质的理解，提升学生的思维品质，形成物理观念，进而提高物理核心素养．