一节高三复习优质课的教学设计与反思*
(鲁迅中学,浙江 绍兴 312030)
章建跃教授提出:让高考复习成为好数学教学,好数学教学的最终目标是实现数学育人,即能够影响学生的思维情怀,能触动学生学会思考、学会学习,从而实现有意义的发展,这也是笔者在教学中一直思考的问题.2018年12月浙江省绍兴市举行了高三复习优质课比赛,笔者有幸参加了此次活动,现把教学过程以及教学的反思感悟记录成文,希望和同行们共勉.
1 课例简录
1.1 回归课本,提出V型
师:绝对值函数是高考的热点和难点之一,在高三复习过程中需引起足够的重视.但高考试题往往源于课本,又高于课本,许多考题的“根”常源于课本.今天我们以课本中的函数“y=|x|”(俗称V形函数)为母函数,通过改变其形式,与大家一起探讨这类函数在解题中的妙用.首先我们来看看V型函数的不同变形.
思考1y=2|x|的图像,可以怎么画?
生1:函数的图像是更陡的一个V型函数,还发现有一个尖尖角过原点.
师:回答得太棒了!大家注意到这位同学提到了两个关键的地方:提到了V型函数的斜率,和我们的母函数相比,斜率发生了变化;还有一个尖尖角,这个尖尖角我们可以称它为顶点.
换句话,可以这样叙述:y=2|x|的图像是正斜率为2、顶点为(0,0)、对称轴为x=0的V型函数.请大家继续完成下面图像的叙述.
思考2y=|x-1|的图像呢?
生2:顶点为(0,0)、正斜率为1的V型函数,其对称轴为x=1.
思考3y=|x-a|的图像呢?
生3:如图1,顶点为(a,0)、正斜率为1的V型函数,其对称轴为x=a.
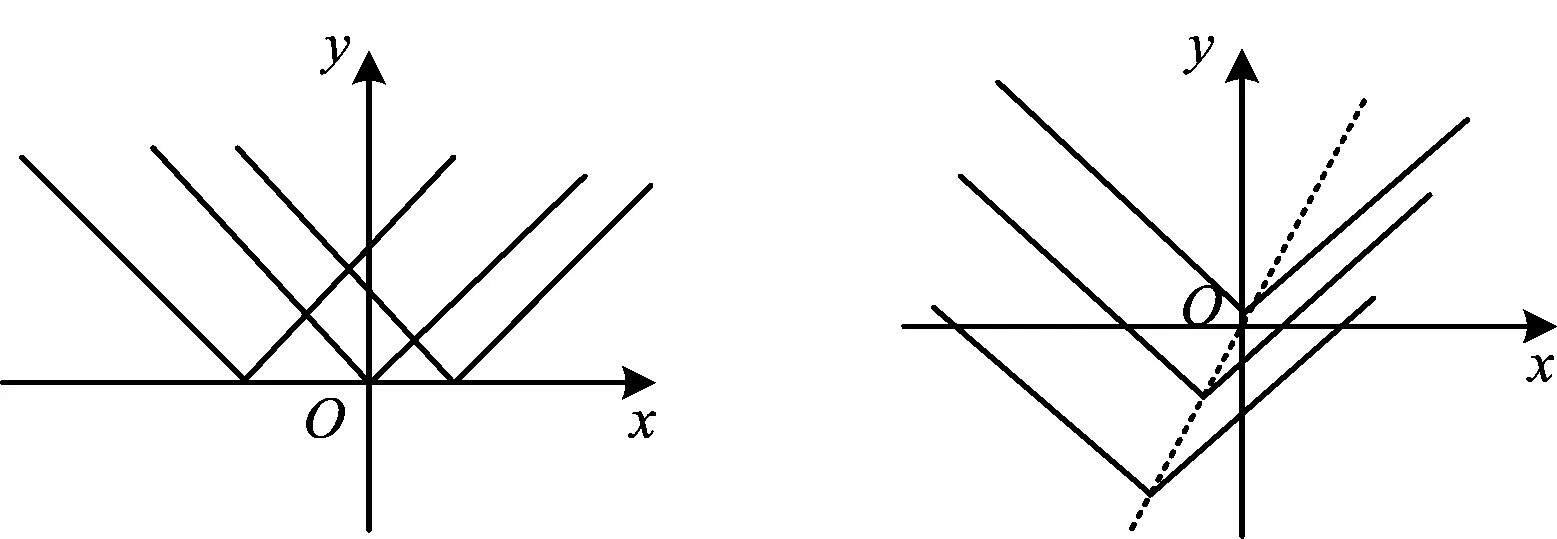
图1 图2
思考4y=|x-a|+2a的图像呢?
生4:如图2,顶点为(a,2a)、正斜率为1的V型函数,其对称轴为x=a.
师:大家试着对顶点取几个特殊值,你还发现顶点运动有什么规律吗?
生5:该V型函数的顶点在y=2x这条直线上运动.
师:这位同学回答得非常准确!在上面的探究过程中,我们把静态的V型函数变成了好玩的动态的V型图.大家是不是要想,这样的动态图应用起来如何呢?请看下面的例1.
设计意图让高三复习课回归教材,通过教材寻找对母函数y=|x|的回忆,明晰y=|x-a|+2a的由来,指出V型函数的特征,提出V型函数模型.
1.2 初试V型,尝试运用
例1已知t为常数,函数y=|x-t|在区间[0,2]上的最大值为5,求t的值______.
变式1已知t为常数,函数y=|x-t|+t在区间[4,5]上的最大值为5,则t的范围为______.

(2017年浙江省数学高考试题第17题)
师:若把y=|x-t|+t中的x的换成g(x),g(x)可以是二次函数、对勾函数等形式,通过换元降维转化成V型模型.
设计意图此题组是本节课的核心,也是学生参与认知构建V型的课堂活动展示区,例1的设计意在让学生初步形成V型模型的基本特征.f(x)=|x-a|的图像是顶点(a,0)在x轴上动的折线.变式2升华到高考真题,并且指出V型函数的构造需要换元降维意识.
1.3 巧构V型,变形使用
师:其实大部分考题中的V型函数,常常隐藏在复杂的代数式中,需要去寻找,需要变形的技巧,请大家看例2.
例2设函数f(x)=|x-a|+x2+2a+1有两个零点,则实数a的范围为______.
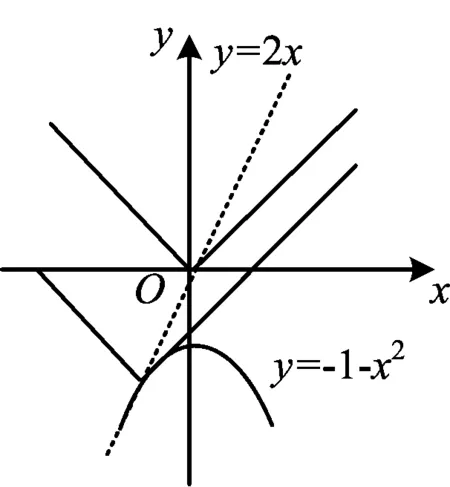
图3

设计意图通过对函数式分离、变形转化,重构V型函数,加强模式的识别与转化.
1.4 再构V型,拓展妙用
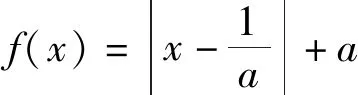
师:这位同学反应真快!大家再想想,既然能在反比例曲线上运动,还可以是其他曲线吗?
生7(破口而出):二次函数上.
生8:三次函数上.
(课堂氛围很活跃.)
师:大家思维真开阔!老师把大家的思路整理后可以统一写成形如f(x)=|x+a|+g(a)的V型函数,顶点在(a,g(a))上运动.最后再考考大家:f(x)=|x+a|+b的图像,其顶点轨迹是什么?
(学生纷纷议论,得到顶点可以随意运动.)
例3已知函数f(x)=x3+3|x-a|,若[f(x)+b]2≤4对任意的x∈[-1,1]恒成立,则3a+b的值为______.
师:这里的V型函数,我们该如何构造呢?
生9:去平方,得|f(x)+b|≤2,即-x2-2≤3|x-a|+b≤-x2+2.如图4,当x∈[-1,1]时,y=3|x-a|+b的图像夹在y=-x2-2与y=-x2+2的图像之间,发现折线顶点(a,b)只能处于(0,-2),即a=0,b=-2,故3a+b=-2.

图4
设计意图提出V型模型特征的丰富性,加入曲线轨迹或者平面上任意运动.条件给出的形态更丰富,指出学生识别题目模型特征的重要性,以及变形能力的重要性.
1.5 课堂小结
师:下面我们来总结今天这节课的重要探究,V型函数和我们之前学过的什么函数类似?
(提示:哪个函数也有开口、对称轴和顶点?)
生(众):二次函数.
两者对比后可以发现有如下的联系(黑板板书):
结束语当V型函数的折线斜率发生变化,意味着V型的翅膀舞动起来,祝大家插上V型的翅膀飞向成功的彼岸!
1.6 课后延展,感悟真题
罗增儒教授曾说:通过有限的典型问题的学习去领悟那种解无限道题的数学机智.正是基于这个视角来审视高考真题,会发现高考试题正是借助本源性问题,进行科学合理地重组、包装,建构出一道简约又不失内涵的考题.而我们的解题教学,就是对考题进行解构、退化,还其“庐山真面目”,识其“真颜”,让学生真切感受解题方法的呈现是自然、和谐的.
例4[1]已知函数f(x)=x3+3|x-a|(其中a∈R).
1)略;
2)设b∈R,若[f(x)+b]2≤4对x∈[-1,1]恒成立,求3a+b的取值范围.
(2014年浙江省数学高考理科试题第22题)
提示[f(x)+b]2≤4⟺|f(x)+b|≤2⟺-x3-2≤3|x-a|+b≤-x3+2.
例5已知函数f(x)=(x-a)2lnx,其中a∈R.
1)略;
2)求实数a的取值范围,对任意的x∈(0,3e],恒有f(x)≤4e2成立.
(2011年浙江省数学高考理科试题第22题)
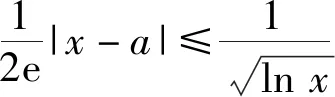
乌申斯基说得好:智慧不是别的,只是组织得很好的知识体系,当学生的头脑强大了,在问题面前运筹帷幄、纵横捭阖,难题自然无处遁形,落花流水了.
2 教学反思
思考1高三复习的定位是什么?
浙江新高考形势及两次选考的冲击,数学的学习可以说是碎片化学习.如何在这样的背景下,提高高三复习的有效性,笔者认为回归教材应是理性的选择.以本课例的绝对值函数学习为例,学生其实非常困惑,总停留在如何去绝对值.为此是否可以换一个方式,顺势而为,留下绝对值,并使之形成模型.基于学生对二次函数已有性质的理解,通过观察、类比、辨析,使“V”型函数的模样逐步清晰,内涵得以丰盈,使知识的展开、方法的形成不再是无本之木、无源之水.因此,高三的复习教学应以“以基础知识的掌握、基本技能的提高、基本思想方法的落实”为原则,围绕“四化建设”进行构建,把高三复习的基础知识系统化,例题选择典型化,思想方法大众化,解题表达规范化,真正让课堂教学由“题型+套路+训练”走向“概念+构建+思维”[2].
思考2如何引入可以让高三的复习课教学更具效果?
当前,高三复习课教学可谓“整课尽是真题飞”!这样做的好处是学生知道是高考题,会激起学生的求知欲、好胜心,及享受问题解决后的成功感;然而,更多的学生看到高考题时会产生畏难情绪,甚至是恐慌心理,导致高考试题价值没有充分挖掘,教学效果就大打折扣[3].本节高三复习课第一稿设计也是以高考题引入,结果发现学生上课效果不理想,改用教材引入后,给学生熟悉的亲切感,甚至让学生体会到教材的重要性,认识到考题往往源于课本,又高于课本.
思考3高三复习教学中,试题讲评在课堂上占很大比重,如何提高这样的上课效率?
教学家杜威曾说:“教学绝对不仅仅是简单地告诉,教学应该是一种过程的经历,一种体验,一种感悟.”它需要学生思维的加盟,有思维的激荡就有不同的想法和做法,数学课只有有了这样的思维主体,才是鲜活的、灵动的、高效的.
笔者参加此次优质课比赛最大的感悟是教学要留给学生自主的空间和时间,让学生更多地参与交流、辨析、思考,让教学“慢”下来,让师生在互动中“说题”.一方面要对高考试题退化、还原、重构,继而进行递推式铺底,搭建“脚手架”,让学生在新的问题情境中学会识别,学会用已有的知识、已有的方法、已有的思想解决新问题;另一方面,让学生充分发表观点、想法,展示其思路历程,只有这样,学生才能获得有意义的发展.

