自适应最大相关峭度反褶积方法诊断齿轮轴承复合故障
吕 轩,胡占齐,周海丽,王 强
自适应最大相关峭度反褶积方法诊断齿轮轴承复合故障
吕 轩,胡占齐※,周海丽,王 强
(1. 燕山大学机械工程学院,秦皇岛 066004;2. 燕山大学自润滑关节轴承共性技术航空科技重点实验室,秦皇岛 066004)
为了解决传统最大相关峭度反褶积(maximum correlated kurtosis deconvolution,MCKD)在故障诊断中容易出现因参数选择不当而影响诊断效果的问题,该文提出了一种基于量子遗传算法(quantum genetic algorithm,QGA)的自适应最大相关峭度反褶积方法(maximum correlated kurtosis deconvolution with quantum genetic algorithm,QMCKD)用于齿轮和轴承复合故障诊断。通过量子遗传算法自适应选择最大相关峭度反褶积的2个关键参数滤波器长度()和反褶积周期()。使用QMCKD处理原始振动信号,提取复合故障信号中的所有单个故障信号,分别对单个故障信号进行频谱分析从而识别故障特征。在对齿面磨损-滚动轴承外圈损伤复合故障诊断中,QMCKD能够识别齿轮故障频率及其2~4倍频,识别轴承故障频率及其2~6倍频,且主要频率成分周围干扰谱线很少,故障类型容易识别。与直接频谱分析和变分模态分解(variational mode decomposition,VMD)相比,该方法在诊断效果上具有优越性。在对齿根裂纹-轴承滚动体损伤复合故障诊断中,QMCKD能够突出齿轮故障频率及其2~5倍频,突出轴承故障频率及其2~8倍频,齿轮和轴承故障特征明显,验证了方法的稳定性。试验结果表明QMCKD能够有效识别复合故障中齿轮和轴承的故障特征,可用于齿轮箱的齿轮、轴承复合故障诊断。
齿轮;轴承;诊断;复合故障;最大相关峭度反褶积;量子遗传算法
0 引 言
齿轮和轴承作为齿轮箱的核心零部件,加工工艺复杂,装配精度要求高,而且工作环境复杂恶劣,容易发生故障。其运行状态决定了整个传动系统的性能,甚至影响系统的使用寿命,若齿轮和轴承发生故障,可能造成巨大的损失。因此许多研究集中于齿轮箱的故障诊断,旨在寻找可靠有效的故障诊断方法[1-4],从而尽早发现故障以防止事故发生。
若齿轮或轴承发生单一故障,往往会引起其他零部件的故障而发展成为复合故障[5]。在复合故障的振动信号中,各个单个故障信号相互耦合,使故障信号的频率特征变得复杂,故障特征难以识别。齿轮箱复合故障诊断的研究已经获得了许多成果,很多方法被证明在齿轮箱复合故障诊断中具有较高的实用价值:如形态分量(morphological component analysis,MCA)[6]及其改进方法[7-8],集合经验模态分解方法(ensemble empirical mode decomposition,EEMD)[9],变分模态分解(variational mode decomposition,VMD)[10-11],最大相关峭度反褶积(maximum correlated kurtosis deconvolution,MCKD)[12],共振稀疏分解(resonance based signal sparse decomposition,RSSD)[13-14],盲源分离法(blind source separation,BSS)[15-16],智能诊断[17],以及多种方法的综合应用[18]均被成功应用于齿轮箱复合故障的诊断中。
在齿轮箱复合故障诊断方法中,最大相关峭度反褶积(MCKD)可以在信噪比很低的情况下提取信号的微弱周期冲击成分,适合强噪声背景下的故障诊断。MCKD在齿轮箱故障诊断中的研究可以分为两类:一类将MCKD作为信号前处理方法,与其他诊断方法相结合作为综合诊断方法。王志坚等[19]在齿轮-轴承复合故障诊断中,使用MCKD对原始信号降噪,提取感兴趣的周期成分,并将降噪后的信号进行自相关函数解调分析,实现齿轮和轴承复合故障诊断,但未对MCKD参数进行自适应选择。Jia等[20]在谱峭度(spectral kurtosis,SK)方法的改进中使用MCKD作为信号的前处理工具突出信号的周期周期脉冲成分,然后应用SK选择MCKD滤波后信号的谐振频带,并将该方法成功应用于轴承早期故障诊断。Hong等[21]在旋转机械复合故障诊断的研究中,分别将MCKD和多尺度小波作为信号前、后处理技术,增强去噪效果,成功实现航空发动机转子复合故障诊断。另一类针对MCKD的计算参数,通过研究参数的自适应选择而实现对MCKD的方法改进。Miao等[22]等提出了一种基于MCKD的改进方法IMCKD,该方法能够自适应选择位移数和反褶积周期,将此方法应用于轴承故障诊断中,成功提取出故障特征,但该方法没有考虑滤波器长度对算法效果的影响。Tang等[12]在MCKD方法改进中提出了AMCKD方法,通过使用布谷鸟搜索算法(cuckoo search algorithm,CSA)对滤波器长度和位移数进行自适应选择,将该方法应用于轴承内、外圈复合故障的诊断中,成功从混合信号中提取出2种故障特征,但该方法没有考虑反褶积周期的波动对计算结果的影响。
决定MCKD诊断效果有2个关键参数:反褶积周期和滤波器长度。反褶积周期的确定需要一定的先验知识,即感兴趣的冲击成分的周期需要提前知道,在实际工况条件下,感兴趣的周期与理论计算出来的值并不完全吻合,从而使其对应的反褶积周期的取值不固定,是在以理论周期为中心的某一范围内波动;滤波器长度的确定一般参考前人的研究成果凭经验确定,且滤波器长度和反褶积周期存在交互作用。这会给参数的选择带来很大的主观因素和难度,容易造成参数的选择不当,对诊断效果造成负面影响。为了克服MCKD在参数选择上的不足,本文提出自适应参数选择的QMCKD方法,充分利用QGA具有全局搜索能力强和计算精度不受种群大小限制等优点[23-25],自动搜寻对应不同类型故障的最优参数组合。将此方法用在行星轮系齿轮和轴承复合故障诊断中,成功分离出齿轮和轴承故障信号,且齿轮和轴承故障特征能够被明显识别,证明了方法的有效性。
1 基于QGA的改进MCKD方法
MCKD是由L Mc Donald等[26]提出,并成功将该方法应用于齿轮齿面剥落的故障诊断中。
QGA是由K H Han等[27]提出,该算法以量子计算的一些概念和理论为基础,用量子位编码来表示染色体,用量子门作用和更新来完成进化搜索,具有以下特点:1)算法性能不受种群大小影响;2)收敛速度快;3)有较强的全局寻优能力。
作为一种有效且稳健的寻优方法,QGA可以在给定的搜索空间内实现全局优化。QGA用于自动搜索MCKD的计算参数和,能够克服主观因素造成的影响,提高故障诊断的准确度。基于此建立了QMCKD方法。
QMCKD在以下2个方面对MCKD进行改进:
1)QMCKD在故障频率的波动范围内自适应选择最优的参数,从而避免通过理论计算得到的与实际情况不符造成的诊断错误。
2)QMCKD在参数寻优过程中充分考虑和的交互作用,从而使二者共同作用使MCKD算法达到最佳的计算效果。避免传统MCKD的参数选择无法充分考虑二者的交互作用而无法得到最优的参数组合,影响诊断效果。
反褶积周期由公式(1)计算。
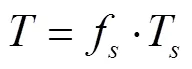
式中f为采样频率,Hz;T为感兴趣的周期,s。
利用QGA对参数进行自适应选择,需要确定一个适应度函数,作为判断寻优结果是否为最优解的依据。种群每进行一次更新,便计算一次适应度函数值,在种群内部通过对比适应度值的大小选出种群群内最优解,通过种群间的最优解对比来决定是否继续对种群进行更新以及种群移动的方向,从而得到最优结果。
本文以经过MCKD方法处理后的反褶积信号的包络熵[28](envelope entropy EE)作为寻优方法的适应度函数,通过反褶积信号的包络熵值作为判断寻优结果好坏的依据。

式中p为()的归一化形式,()为信号()经Hilbert 解调后得到的包络信号。
若MCKD方法的参数选择准确,则反褶积信号会包含明显的周期性冲击成分,其包络熵值较小;若MCKD方法的参数选择不当,则反褶积效果欠佳,周期性冲击成分不明显,包络熵值较大。因此以适应度函数值最小作为判断是否得到最优结果的依据。
QMCKD对齿轮和轴承复合故障诊断的步骤如下:
1)根据齿轮箱的运行参数,以及齿轮和轴承的故障频率计算公式分别计算二者的特征周期T和T;根据实际情况设置特征周期的选择范围[T-T1,T+T1],[T-T1,T+T1],其中T1、T1分别为齿轮与轴承特征周期允许的最大波动数值。将特征周期的选择范围代入式(1)计算对应的反褶积周期,分别得到齿轮和轴承反褶积周期T和T的选择范围。
2)设置QGA的参数,本文中种群大小设为30,最大迭代次数设为50,滤波器长度的选择范围设置为[2,700],反褶积周期的参数根据步骤1)设置。
3)执行QGA寻优计算,通过评估适应度值自适应选择最优的参数组合[,]。分别得到齿轮和轴承的最优MCKD参数组合[L,T],[L,T]。L,T为齿轮故障信号的MCKD参数;L,T为轴承故障信号的MCKD参数。
4)将最优参数组合代入到MCKD中,分别对输入信号进行MCKD处理,得到齿轮和轴承的故障信号。
5)对齿轮故障信号做频谱分析,轴承故障信号做包络分析。
6)根据提取出的故障特征分别对齿轮和轴承做故障判断。
2 仿真信号分析
设置齿轮箱的复合故障仿真信号如式(3),以仿真信号作为反褶积对象,通过对仿真信号的处理验证QMCKD的有效性。

式中()为模拟齿轮故障的信号;z为模拟故障齿轮啮合频率,Hz;为啮合频率的谐波数,A为啮合频率次谐波的幅值,m/s2;()为周期冲击成分,模拟轴承故障信号;()为高斯白噪声成分,用来模拟噪声信号。()由个衰减系数为、共振频率为f(Hz)的单冲击信号组成,T(s)为相邻2次冲击之间的时间间隔,故障频率f(Hz)=1/T;τ为第次冲击相对于周期T的微小波动,服从零均值正态分布,标准差为转频的0.5%;()为单位阶跃函数。A(m/s2)为幅值为0(m/s2)的调制信号,f为轴承轴的转频,Hz。仿真信号各参数值如表 1所示。
仿真信号的采样频率12 000 Hz,采样点数为12 000,将表1中各参数代入式(3),得到仿真齿轮故障信号、轴承故障冲击信号和加入噪声的合成信号的时域及频域,如图1所示。由图1a,图1c和图1e可见,加入噪声后,齿轮故障信号和轴承故障信号的周期成分完全被湮没。从混合信号的功率谱图1f及其包络谱图1g可以看出,齿轮的故障频率和轴承的故障频率无法识别,故障特征完全被湮没。
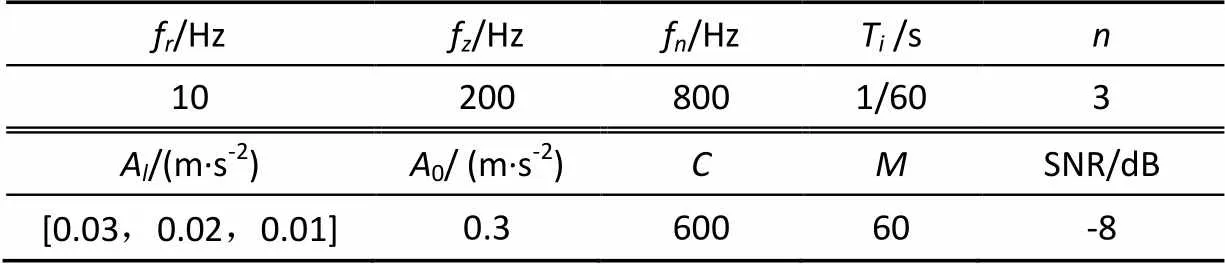
表1 仿真信号参数值
注:f为轴承转频,Hz;f为模拟故障齿轮啮合频率,Hz;f为共振频率,Hz;T为相邻2次冲击之间的时间间隔,s;为模拟齿轮啮合频率谐波数;A为啮合频率幅值,m·s-2;0为调制信号幅值,m·s-2;为衰减系数;为冲击信号个数;SNR为白噪声信噪比,dB。
Note: fis rotational frequency of bearing, Hz;fis the frequency to simulate meshing frequency of faulty gear, Hz;fis resonant frequency, Hz;Tis the time interval of two adjacent impacts, s;is harmonic number of the meshing frequency;Ais the amplitude of meshing frequency, m·s-2;0is amplitude of modulated signal, m·s-2;is attenuation coefficient;is the number of impact signals; SNR is signal-to-noise ratio of white noise, dB.
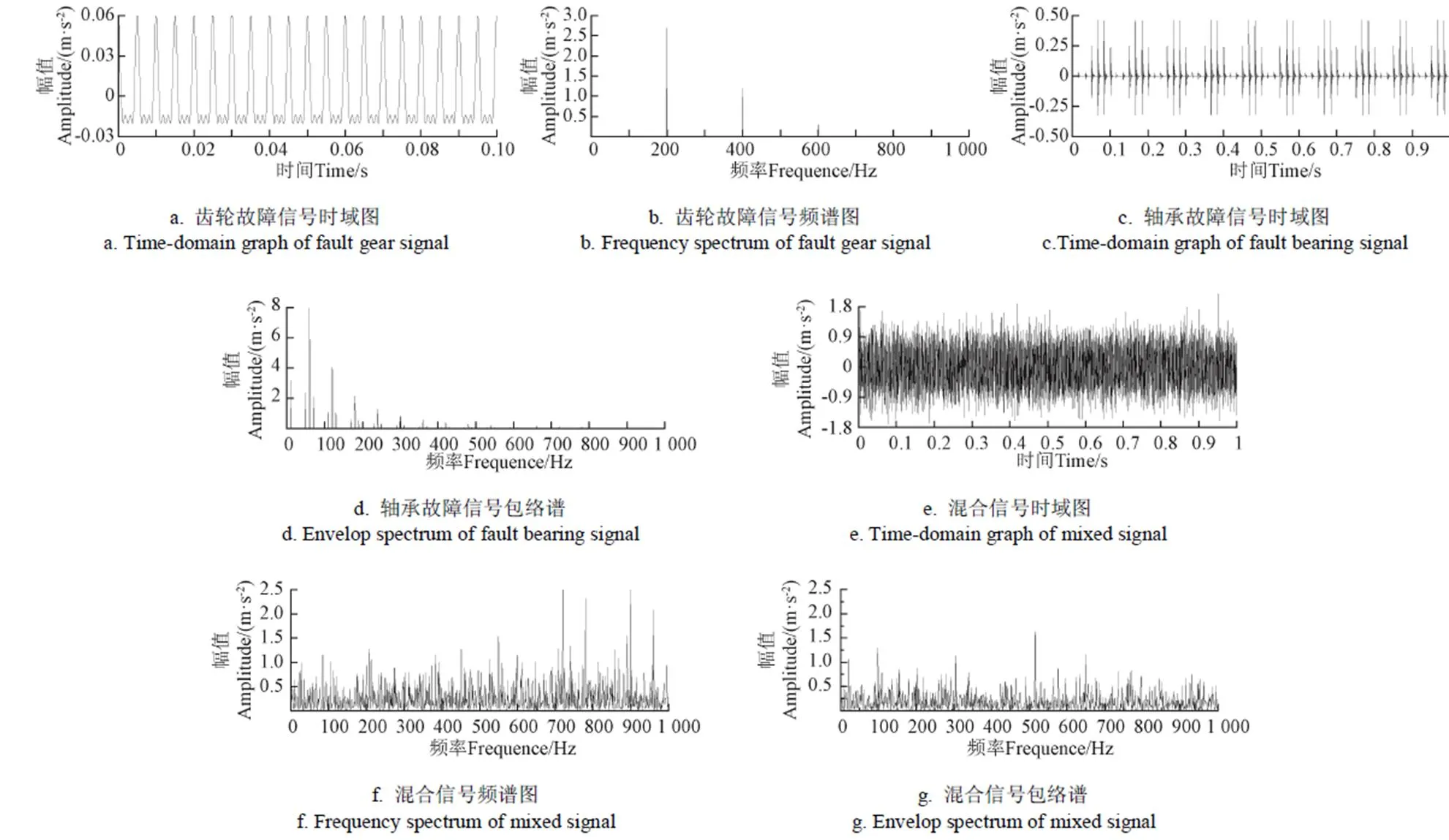
图1 仿真信号的时域图和频谱图
根据式(1),计算出齿轮和轴承故障仿真信号的反褶积周期分别为60和200。在对试验设备的输入转速监测统计中发现,齿轮与轴承特征周期允许的最大波动数值T1、T1均小于20(T1、T1的取值可根据设备运行情况或监测值确定),因此仿真信号齿轮和轴承的寻优范围分别设置为[40,80]和[180,220]。用QGA分别对齿轮故障特征和轴承故障特征的MCKD参数组合进行寻优选择,寻优结果如图2a和图2b所示。齿轮和轴承故障信号最小的包络熵值分别出现在第40代和第36代,得到齿轮故障信号最优参数组合为=133,=59;轴承故障信号最优参数组合=530,=198。将寻优得到的参数代入MCKD中对混合信号进行处理,分别得到图2c和图2d所示的齿轮故障信号和轴承故障信号。为了便于观察时域信号的周期成分,齿轮故障信号截取前0.1 s的信号,轴承故障信号截取前1 s的信号。从图中可以看出经过QMCKD处理后的信号突出了特征周期成分。
图2e为齿轮故障信号的功率谱,图中主要的频率成分为齿轮的啮合频率f及其倍频2f和3f。与图1f相比,齿轮的故障特征被明显识别出来。从图2f所示的轴承故障信号包络谱中可以看到,轴承故障频率f及其倍频nf(=2,…,6)成分明显。与图1g相比,轴承故障频率及其高次倍频成分得到突出,轴承的故障特征容易识别。
噪声信号可以将齿轮和轴承的故障特征湮没,使直接频谱分析无法有效提取二者的故障信息。混合信号经过QGA-MCKD方法处理后,分别突出了齿轮和轴承的特征周期成分,而且在频谱图中可以很容易提取出二者的故障特征成分。
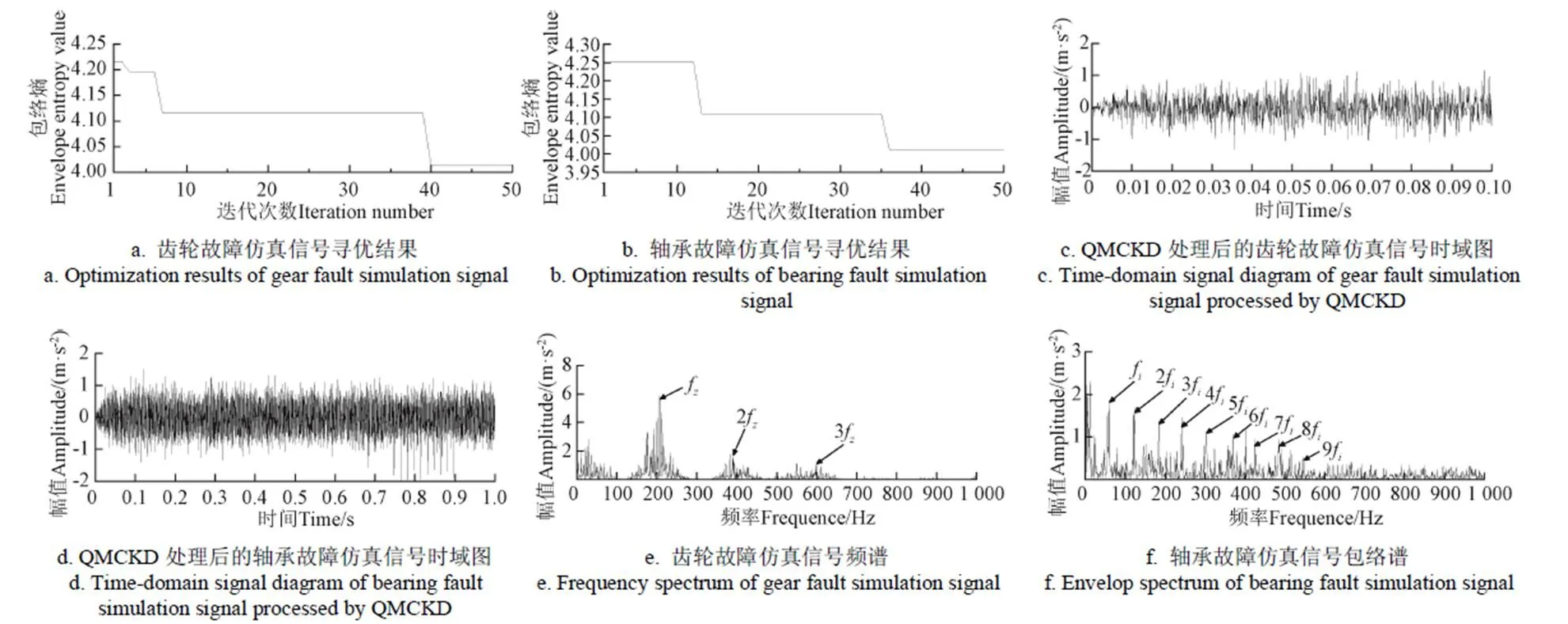
图2 仿真信号的QMCKD诊断结果
3 验证试验
3.1 齿面磨损-滚动轴承外圈损伤复合故障诊断试验
故障信号的采集基于美国SpectraQuest公司的WTDS2010齿轮箱传动故障诊断综合试验台,附带齿轮和轴承故障替换套件,如图3a所示。试验台由可变频交流电机驱动,定轴轮系为输入端,行星轮系为输出端。在试验台上设置的复合故障为一个行星轮磨损和滚动轴承外圈损伤,磨损齿轮与故障轴承分别如图3b和图3c所示。传感器为美国PCB公司352C68型ICP加速度传感器(灵敏度100 mV/g),安装在行星轮系外壳体上,采样频率3 000 Hz,传感器安装位置如图3d所示。设置电机转速为2 400 r/min,采样频率为3 000 Hz,当试验台运行稳定后开始采集加速度信号,采样时间8 s。经过计算得到各级齿轮和轴承的特征频率如表2所示。

1.交流电机 2.扭矩传感器和编码器 3.定轴齿轮箱 4.轴承径向负载 5.行星齿轮箱 6.制动器
齿面均匀磨损时,啮合频率及其谐波分量nf(=1,2,…)在频谱图上的位置保持不变,但其幅值大小发生改变,而且高次谐波幅值相对增大较多[29]。轴承外圈出现故障时,轴承外圈的故障频率及其高次谐波在故障信号的包络谱中是主要的频率成分。
截取试验台稳定运行中的8 192个点做为故障信号,信号的时域图和频谱图如图4所示。在故障信号的频谱图中可以看到,在低频部分除了有行星齿轮啮合频率成分,还能明显看到其2倍频成分,啮合频率的3倍频虽然幅值较小,但仍然可以识别。图4b为故障信号的包络谱图,图中轴承的故障频率成分无法识别。
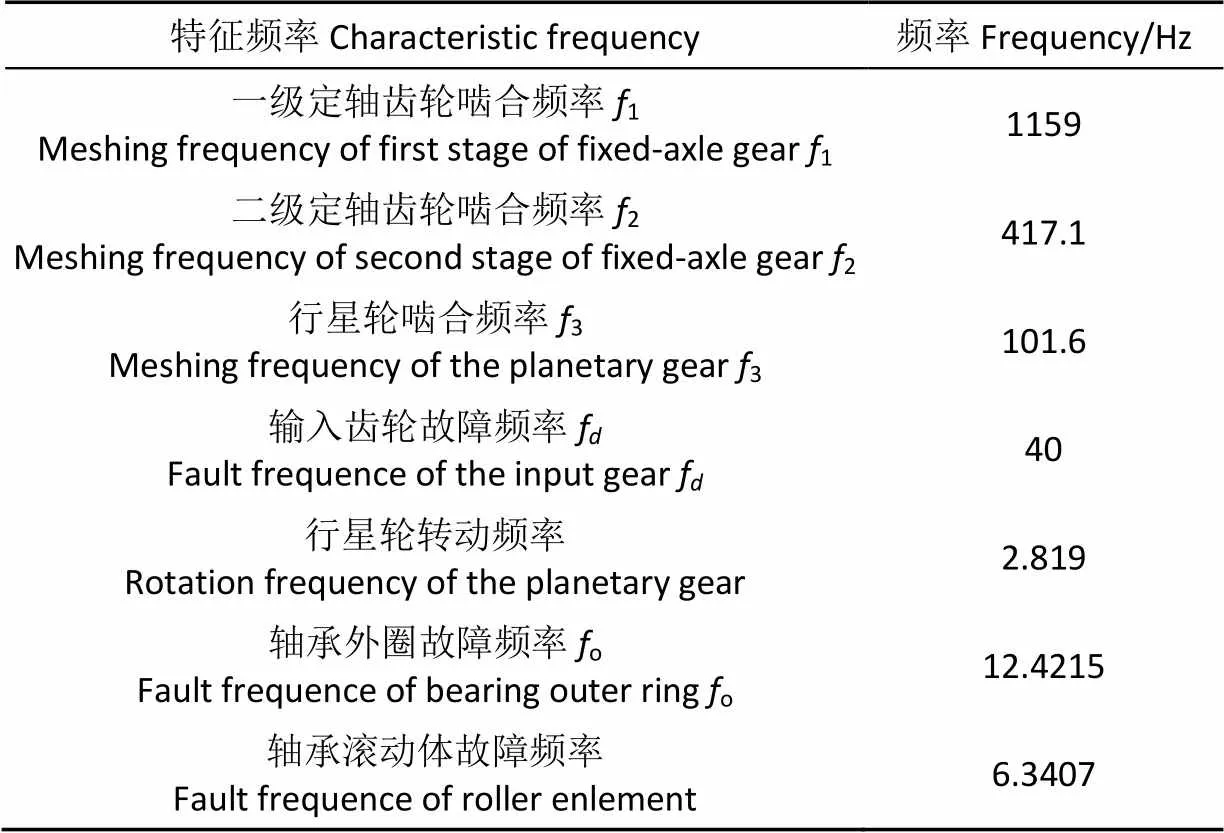
表2 各级齿轮啮合频率以及轴承的故障频率
为了与齿面磨损故障信号对比,将试验台的可替换零件全部换为无故障零件,在相同传感器安装位置和相同采集参数的条件下,得到图5a所示试验台无故障状态信号的频谱。图5a中行星轮啮合频率3及其2倍频23成分较明显,与图5b故障状态信号频谱图对比可以看出,故障状态3的幅值略小于正常状态的幅值,但故障状态23的幅值明显大于正常状态23的幅值,且故障状态的33也可识别,可以识别出齿轮的磨损故障。但在图5b中可以发现主要的特征频率周围存在较多的干扰谱线,故障特征不容易识别。在0~1 200 Hz频段内,峰值最明显的成分出现在400~600 Hz,而能够反映行星齿轮故障特征的频率几乎无法识别,容易误判为二级定轴齿轮故障。为此,需要滤除干扰频率的影响,对故障信号进行MCKD处理。

图4 故障信号时频域图
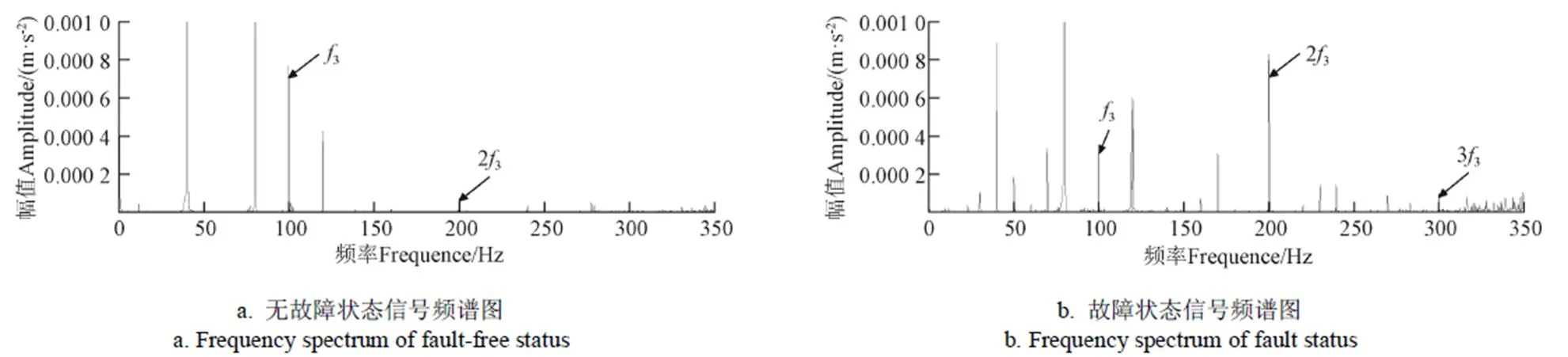
图5 试验台无故障状态和故障状态频谱对比图
根据式(1),计算出齿轮和轴承故障信号的分别为29和242。对试验台在该故障状态下的运行状态监测发现,故障齿轮的特征周期波动范围小于9 s,故障轴承的波动范围设为最大20 s,因此齿轮和轴承的寻优范围分别设置为[20,38]和[222,262]。用QGA分别对故障信号的齿轮故障特征和轴承故障特征的MCKD参数组合和进行寻优选择,寻优结果如图6a和6b所示。齿轮和轴承故障信号最小的包络熵值分别出现在第25代和第26代,得到齿轮故障信号最优参数组合为=201,=30;轴承故障信号最优参数组合=166,=248。
将寻优得到的参数代入MCKD中对故障信号进行处理,分别得到图6c和6d所示的齿轮故障信号和轴承故障信号。图6e为齿轮故障信号的频谱图,图中主要频率成分为行星齿轮啮合频率3及其2、3和4倍频。与图4c和4d相比,齿轮故障特征频率3、23和33成为主要频率成分;在图4d中,4f被完全湮没,无法识别,而图6e中,43虽然幅值很小,但仍然可以辨识。图6e中23的幅值为0.006,图4d中23的幅值为0.000 8,幅值增大7.5倍,故障特征可明显被识别。故障信号经过处理后干扰频率成分明显较少,突出主要频率成分。在图6f所示的轴承故障信号包络谱图中,轴承的故障频率o及其倍频o(=2,…,6)成分十分明显,高次倍频成分也得以体现。较图4b轴承故障特征更加明显且容易识别。这些结果表明QMCKD方法可以将湮没在背景噪声中的复合故障成分有效提取,证明了方法的有效性和实用性。
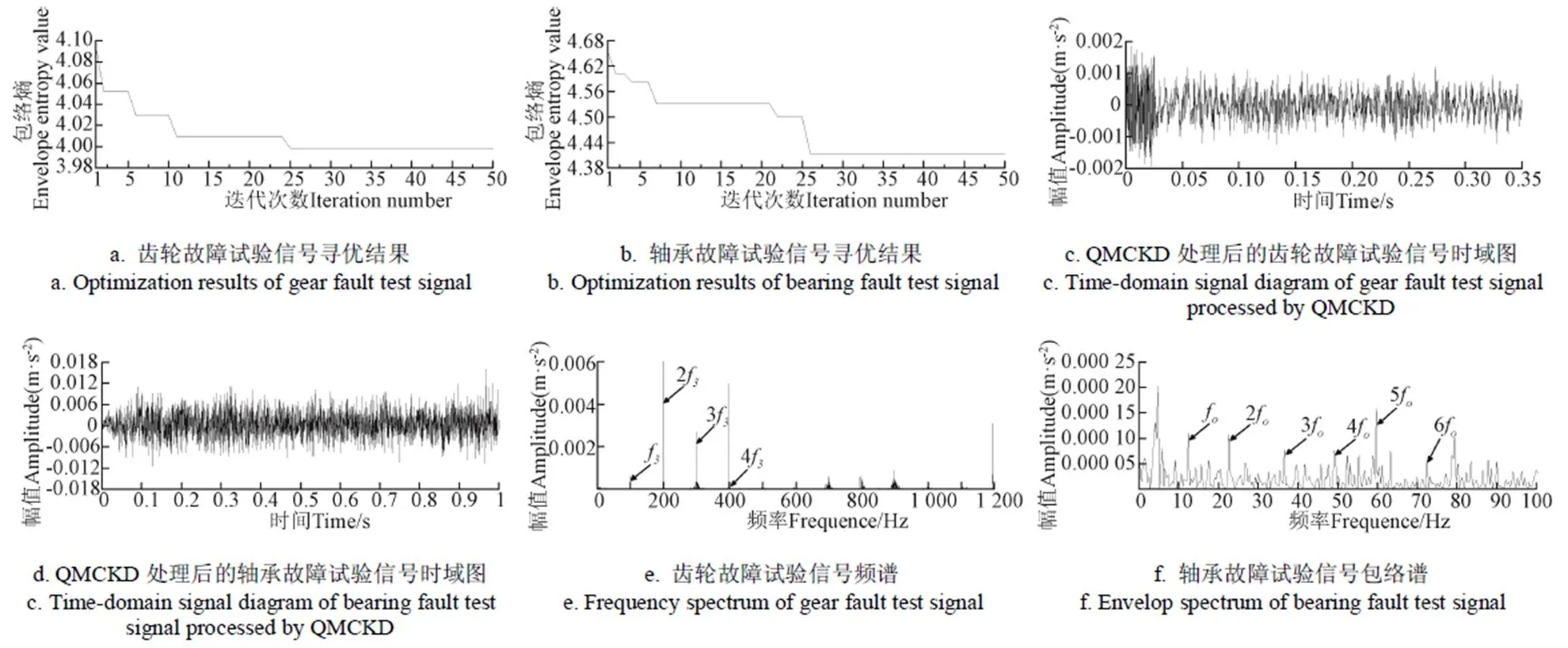
图6 故障信号的QMCKD诊断结果
为了验证本文方法诊断效果的优越性,将QMCKD与VMD对同一故障信号的诊断效果做对比。
故障信号经过VMD分解得到3个本征模态分量(intrinsic mode functions,IMF)。从图7所示的频谱图可以看出,仅在IMF1中出现行星齿轮啮合频率3和23成分,但3的幅值仅为健康状态对应幅值37%,无法反映齿轮磨损故障;从图7f和图7i中可以看出,IMF2和IMF3中出现轴承的故障频率及其2倍频成分,但干扰谱线较多,且高次倍频成分无法识别,不容易对轴承外圈故障进行判断。应用VMD仅识别出轴承的故障特征,但故障特征不明显,特征频率成分受到无关谱线的干扰,故障类型不易判断。
对比图7b、图7e、图7h与图6e,经过QMCKD处理后的齿轮故障信号的故障频率及其倍频成分突出,且倍频成分的幅值明显大于图5a中对应频率成分的幅值,故障特征容易识别。对比图7c、图7f、图7i与图6f,经过QMCKD处理后的轴承故障信号包络谱主要频率成分清晰,干扰谱线很少,轴承故障频率的高次倍频成分也得到突出,轴承的故障特征容易识别。这些结果说明QMCKD对齿面磨损-滚动轴承外圈故障的诊断效果优于VMD。
QMCKD可以充分发挥MCKD在信号处理中的优势,突出感兴趣的周期成分。经过QMCKD处理后的信号周期成分更明显,特征频率更容易识别,能够更有效地对齿轮箱的复合故障进行分离。
3.2 齿根裂纹-轴承滚动体损伤复合故障诊断试验
为了验证本文方法的有效性和稳定性,将QMCKD应用于定轴齿根裂纹-行星齿轮轴承滚动体损伤的复合故障诊断中。
故障信号的时域图和频谱图如图8所示。在图8d中可以看到,一级定轴输入齿轮故障频率f及其2、3倍频成分明显,可以判断为齿根裂纹故障,但在图8c中0~1 000 Hz频段,其故障特征并不明显,而频率成分最明显的为二级定轴齿轮啮合频率及其倍频,容易判断为二级定轴齿轮故障。图8b为故障信号的包络谱图,在图中无法识别轴承的故障特征。
根据式(1),计算出齿轮和轴承故障信号的分别为40和237,的寻优范围分别设置为[20,60]和[217,257]。用QGA分别对故障信号的齿轮故障特征和轴承故障特征的MCKD参数组合和进行寻优选择,寻优结果如图9a和图9b所示。齿轮和轴承故障信号最小的包络熵值分别出现在第26代和第39代,得到齿轮故障信号最优参数组合为=201,=55;轴承故障信号最优参数组合=480,=232。
使用QMCKD对故障信号进行处理,分别得到图9c和图9d所示的齿轮故障信号和轴承故障信号。图9e为齿轮故障信号的频谱图,图中主要频率成分为故障齿轮转频(齿轮故障频率)f及其倍频nf(=2, 3, 4, 5)。图9e中f、2f和3f幅值分别为图8d中对应幅值的2.7倍、40%和1.7倍,经过QMCKD处理后的信号齿轮故障信号仅2f的幅值增大,且齿轮故障频率的高次倍频成分得到突出,在高频段干扰故障判断的频率成分被滤除。故障信号经过处理后干扰频率成分明显较少,突出主要频率成分。在图9f所示的轴承故障信号包络谱图中,轴承的故障频率f成分十分明显,高次倍频nf(=2, 3, 4, 5, 6, 7, 8)也得以体现。较图8b轴承故障特征更加明显且容易识别。这些结果表明QMCKD适用于不同类型的复合故障诊断,证明了方法的有效性和稳定性。
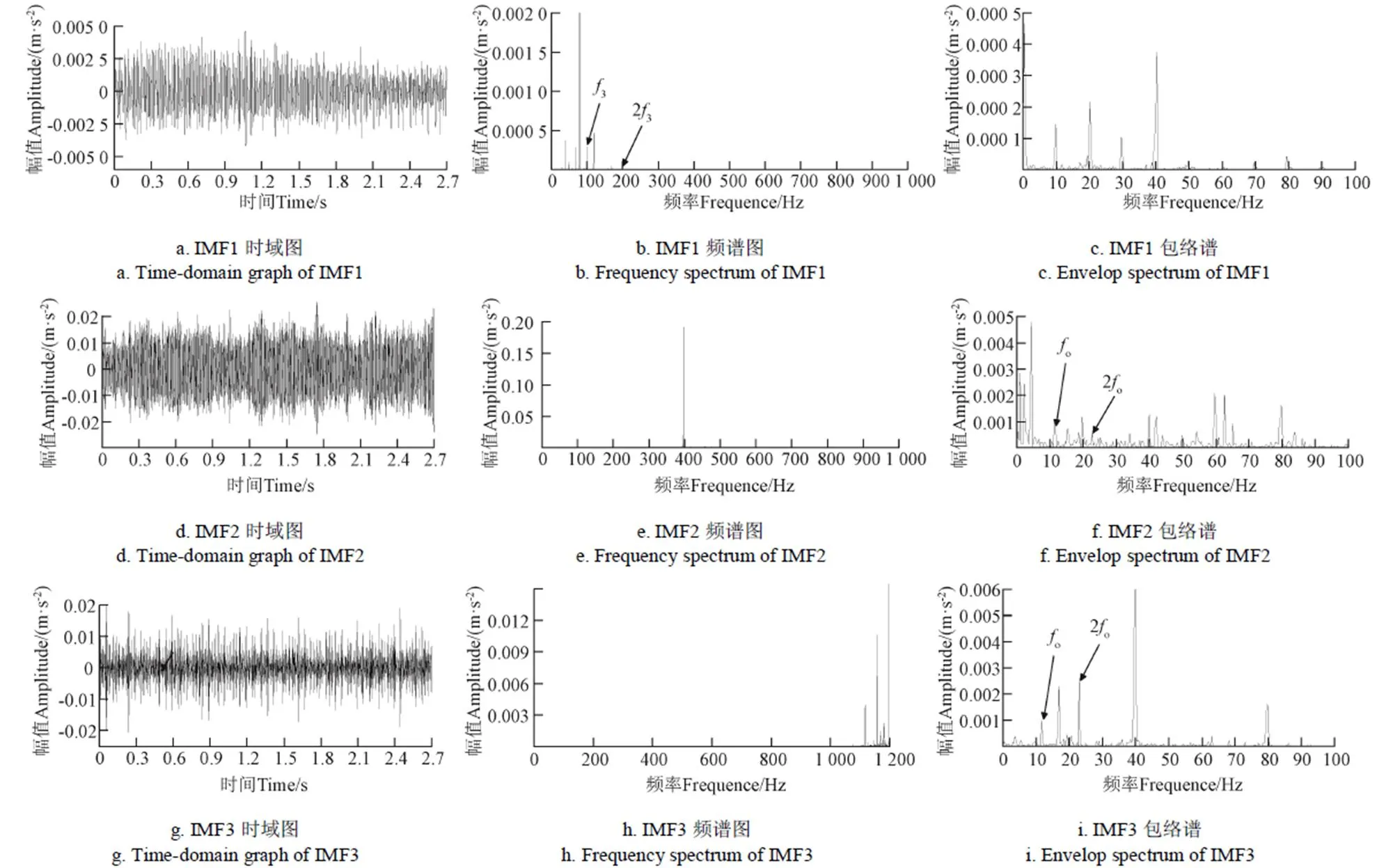
注:IMF1、IMF2、IMF3分别表示第一、第二、第三本征模态函数分量。下同。

图8 复合故障信号的时频域图

图9 复合故障信号的QMCKD诊断结果
4 结 论
本文提出一种基于QGA的自适应MCKD方法(QMCKD),旨在改进MCKD在参数选择上的不足,用以解决齿轮箱齿轮-轴承复合故障诊断的难题。本方法利用QGA在全局参数寻优功能的优势,自适应选择MCKD的2个关键参数反褶积周期和滤波器长度,主要结论如下:
1)仿真结果表明,由于无法有效滤除噪声的干扰,直接频谱分析无法有效提取齿轮和轴承的故障特征。混合信号经过QMCKD处理后,噪声成分被有效滤除,在齿轮故障信号的频谱中,齿轮故障频率及其2~3倍频成分明显,在轴承故障信号的包络谱中,轴承故障频率及其2~9倍频成分明显,齿轮和轴承故障特征容易识别。验证了方法的有效性。
2)在与变分模态分解共同对齿面磨损-滚动轴承外圈损伤复合故障诊断的对比中,QMCKD能够在复合故障信号中分离出齿轮故障信号和轴承故障信号。齿轮故障信号功率谱中,突出齿轮故障频率及其2~4倍频成分,轴承故障信号包络谱中,突出轴承故障频率及其2~6倍频成分,故障特征明显。而VMD仅分别识别出齿轮和轴承的故障频率及其2倍频成分,故障特征无法识别。且经过QMCKD处理后的齿轮和轴承故障信号干扰谱线更少,验证了方法的优越性。
3)在对齿根裂纹-轴承滚动体损伤复合故障实验信号的处理中,QMCKD成功识别出齿轮故障频率及其2~5倍频,识别出轴承故障频率及其2~8倍频,齿轮和轴承故障特征明显,验证了方法的稳定性。
[1] Pan Haiyang, Yang Yu, Li Xin, et al. Symplectic geometry mode decomposition and its application to rotating machinery compound fault diagnosis[J]. Mechanical Systems & Signal Processing. 2019, 114(1): 189-211.
[2] He Shuilong, Chen Jinglong, Zhou Zitong, et al. Multifractal entropy based adaptive multiwavelet construction and its application for mechanical compound-fault diagnosis[J]. Mechanical Systems & Signal Processing. 2016, 76-77(1): 742-758.
[3] Wang Tianyang, Chu Fulei, Han Qinkai, et al. Compound faults detection in gearbox via meshing resonance and spectral kurtosis methods[J]. Journal of Sound and Vibration. 2017, 392(1): 367-381.
[4] 马朝永,盛志鹏. 胥永刚,等. 基于自适应频率切片小波变换的滚动轴承故障诊断[J]. 农业工程学报,2019,35(10):34-41. Ma Chaoyong, Sheng Zhipeng, Xu Yonggang, et al. Fault diagnosis of rolling bearing based on adaptive frequency slice wavelet transform[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(10): 34-41. (in Chinese with English abstract)
[5] Dhamande L S, Chaudhari M B. Compound gear-bearing fault feature extraction using statistical features based on time-frequency method[J]. Measurement. 2018, 125(1): 63-77.
[6] Cai Gaiai, Chen Xuefeng, He Zhengjia. Sparsity-enabled signal decomposition using tunable Q-factor wavelet transform for fault feature extraction of gearbox[J]. Mechanical Systems and Signal Processing. 2013, 41(1/2): 34-53.
[7] Yu Dejie, Wang Min, Cheng Xiangmin. A method for the compound fault diagnosis of gearboxes based on morphological component analysis[J]. Measurement. 2016, 91(1): 519-531.
[8] 李辉,郑海起,唐力伟. 基于改进形态分量分析的齿轮箱轴承多故障诊断研究[J]. 振动与冲击,2012, 31(12):135-140. Li Hui, Zheng Haiqi, Tang Liwei. Bearing multi-fault diagnosis based on improved morphological component analysis[J]. Journal of Vibration and Shock. 2012, 31(12): 135-140. (in Chinese with English abstract)
[9] Jiang Hongkai, Li Chengliang, Li Huaxing. An improved EEMD with multiwavelet packet for rotating machinery multi-fault diagnosis[J]. Mechanical Systems & Signal Processing. 2013, 36(2): 225-239.
[10] 杨宇,罗鹏,程军圣. 广义变分模态分解及其在齿轮箱复合故障诊断中的应用[J]. 中国机械工程. 2017(9):1069-1073. Yang Yu, Luo Peng, Cheng Junsheng. GVMD and its applications in composite fault diagnosis for gearboxes[J]. China Mechanical Engineering. 2017(9): 1069-1073. (in Chinese with English abstract)
[11] 王志坚,常雪,王俊元,等. 排列熵优化改进变模态分解算法诊断齿轮箱故障[J]. 农业工程学报,2018,34(23):59-66. Wang Zhijian, Chang Xue, Wang Junyuan, et al. Gearbox fault diagnosis based on permutation entropy optimized variational mode decomposition[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(23): 59-66. (in Chinese with English abstract)
[12] Tang Guiji, Wang Xiaolong, He Yuling. Diagnosis of compound faults of rolling bearings through adaptive maximum correlated kurtosis deconvolution[J]. Journal of Mechanical Science & Technology. 2016, 30(1): 43-54.
[13] Zhang Dingchen, Yu Dejie. Multi-fault diagnosis of gearbox based on resonance-based signal sparse decomposition and comb filter[J]. Measurement. 2017, 103(1): 361-369.
[14] 黄文涛,付强,窦宏印. 基于自适应优化品质因子的共振稀疏分解方法及其在行星齿轮箱复合故障诊断中的应用[J]. 机械工程学报. 2016, 52(15):44-51. Huang Wentao, Fu Qiang, Dou Hongyin, Resonance-based sparse signal decomposition based on the quality factors optimization and its application of composite fault diagnosis to planetary gearbox [J]. Journal of Mechanical Engineering. 2016, 52(15): 44-51. (in Chinese with English abstract)
[15] Li Zhixiong, Yan Xinping, Tian Zhe, et al. Blind vibration component separation and nonlinear feature extraction applied to the nonstationary vibration signals for the gearbox multi-fault diagnosis[J]. Measurement Journal of the International Measurement Confederation. 2013, 46(1): 259-271.
[16] 杨宇,何知义,李紫珠,等. ASTFA-BSS方法及其在齿轮箱复合故障诊断中的应用[J]. 中国机械工程. 2015, 26(15):2051-2055, 2061. Yang Yu, He Zhiyi, Li Zizhu, et al. ASTFA-BSS method and its application in composite fault diagnosis for gearbox [J]. China Mechanical Engineering. 2015, 26(15): 2051-2055, 2061. (in Chinese with English abstract)
[17] 陈如清,李嘉春,尚涛,等. 改进烟花算法和概率神经网络智能诊断齿轮箱故障[J]. 农业工程学报, 2018, 34(17):192-198. Chen Ruqing, Li Jiachun, Shang Tao, et al. Intelligent fault diagnosis of gearbox based on improved fireworks algorithm and probabilistic neural network[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(17): 192-198. (in Chinese with English abstract)
[18] Li Bing, Zhang Peilin, Tian Hao, et al. A new feature extraction and selection scheme for hybrid fault diagnosis of gearbox[J]. Expert Systems with Applications. 2011, 38(8): 10000-10009.
[19] 王志坚,寇彦飞,王俊元,等.基于最大相关峭度反褶积的齿轮箱复合故障特征提取[J]. 噪声与振动控制,2017(3):173-176.
Wang Zhijian, Kou Yanfei, Wang Junyuan, et al. A feature extraction method for gearboxes with compound faults based on MCKD[J]. Noise and Vibration Control, 2017(3):173-176. (in Chinese with English abstract)
[20] Jia Feng, Lei Yaguo, Shan Hongkai, et al. Early fault diagnosis of bearings using an improved spectral kurtosis by maximum correlated kurtosis deconvolution[J]. Sensors. 2015, 15(11): 29363-29377.
[21] Hong Lianhuan, Liu Xiaobo, Zuo Hongyan. Compound fault diagnosis of rotating machinery based on adaptive maximum correlated kurtosis deconvolution and customized multiwavelet transform[J]. Measurement Science and Technology. 2018, 29(11). doi: 10.1109/CCDC.2015.7162598
[22] Miao Yonghao, Zhao Ming, Lin Jing, et al. Application of an improved maximum correlated kurtosis deconvolution method for fault diagnosis of rolling element bearings[J]. Mechanical Systems & Signal Processing. 2017, 92(1): 173-195.
[23] Han K H, Park K H, Lee C H, et al. Parallel quantum-inspired genetic algorithm for combinatorial optimization problem[C]// Congress on Evolutionary Computation. IEEE, 2001.
[24] Li Bin, Zhuang Zhenquan. Genetic Algorithm Based-On the Quantum Probability Representation[C]// International Conference on Intelligent Data Engineering & Automated Learning. Springer-Verlag, 2002.
[25] Zhang Gexiang, Jin Weidong, Li Na. An improved quantum genetic algorithm and its application[C]// Rough Sets, Fuzzy Sets, Data Mining, & Granular Computing, International Conference, Rsfdgrc, Chongqing, China, May. DBLP, 2003.
[26] L Mc Donald G, Zhao Q, J Zuo M. Maximum correlated Kurtosis deconvolution and application on gear tooth chip fault detection[J]. Mechanical Systems & Signal Processing. 2012, 33(1): 237-255.
[27] K H Han, J H Kim. Genetic quantum algorithm and its application to combinatorial optimization problem. Evolutionary Computation, 2000 Proceedings of the 2000 Congress on; 2002.
[28] 唐贵基,王晓龙. 自适应最大相关峭度解卷积方法及其在轴承早期故障诊断中的应用[J]. 中国电机工程学报. 2015(6):1436-1444. Tang Guiji, Wang Xiaolong. Adaptive maximum correlated kurtosis deconvolution method and its application on incipient fault diagnosis of bearing[J]. Proceedings of the Chinese Society for Electrical Engineering. 2015(6): 1436-1444. (in Chinese with English abstract)
[29] 盛兆顺. 设备状态监测与故障诊断技术及应用[M]. 北京:化学工业出版社,2003.
Compound fault diagnosis method for gear bearing based on adaptive maximum correlated kurtosis deconvolution
Lü Xuan, Hu Zhanqi※, Zhou Haili, Wang Qiang
(1.,,,066004,; 2.,,, 066004,)
Gear boxes often operate in harsh working environment, the core components, gears and bearings, are prone to malfunction. Therefore, in order to find the fault as early as possible and prevent the occurrence of the accident, a reliable and effective fault diagnosis method is needed. Maximum correlated kurtosis deconvolution (MCKD) is an effective diagnosis method which can be applied to the processing of compound fault vibration signal of gear boxes. But the diagnosis performance of MCKD is directly affected by two key parameters (filter length and deconvolution period). In order to overcome the insufficiency of MCKD in parameter selection and improve the diagnosis quality, an adaptive maximum correlated kurtosis deconvolution gearbox fault diagnosis method method is proposed based on quantum genetic algorithm (QMCKD). The key parameters of MCKD are adaptively selected using quantum genetic algorithm (QGA), the raw signal is processed by QMCKD to extracte every single fault signal from the compound fault signal, and the single fault signals are analyzed by frequency spectrum method to identify the fault features. The superiority of QMCKD was verified by comparing with variational mode decompositio (VMD). The results show that QMCKD can develop the advantages of MCKD in signal processing and highlight the periodic components of interest, after processed by QMCKD, the periodic components of the signal are more obvious, the characteristic frequencies are much easier to identify, and the compound faults of the gearbox can be separated more effectively. QMCKD was applied to the compound fault diagnosis of planetary gear tooth surface wear-rolling bearing outer ring damage. In the frequency spectrum of the gear fault signal, the main frequency components were the gear meshing frequency and its 2 times and 3times, the 4 times meshing frequency also could be identified, and the amplitude of the harmonics of meshing frequency were significantly larger than that of health state. The frequency components reflected the fault features of planetary gear tooth surface wear. The fault frequency of the outer ring damage and its high-order harmonics could be completely highlighted in the envelop spectrum of the separated gearing fault signal which reflected the fault features of rolling bearing outer ring damage. In dealing with the experimental signal of compound fault of tooth root crack and bearing rolling element damage, QMCKD successfully identifies the gear fault frequency and its 2-5 times frequency, and the bearing fault frequency and its 2-8 times frequency. The fault characteristics of gear and bearing are obvious, which verifies the stability of the method. QMCKD can effectively identify the fault characteristics of gears and bearings in complex faults, and can be used in the fault diagnosis of gears and bearings in gearboxes.
gear; bearing; diagnosis; compound fault; maximum correlation kurtosis deconvolution; quantum genetic algorithm
2018-12-06
2019-03-28
河北省军民融合项目(2018B100)
吕 轩,博士生,主要研究方向旋转机械故障诊断。Email:jaylvxuan@163.com
胡占齐,教授,主要研究方向机械设备故障诊断。E-mail:ronghu118@163.com。
10.11975/j.issn.1002-6819.2019.12.006
TH165+.3;TH17
A
1002-6819(2019)-12-0048-10
吕 轩,胡占齐,周海丽,王 强. 自适应最大相关峭度反褶积方法诊断齿轮轴承复合故障[J]. 农业工程学报,2019,35(12):48-57. doi:10.11975/j.issn.1002-6819.2019.12.006 http://www.tcsae.org
Lü Xuan, Hu Zhanqi, Zhou Haili, Wang Qiang. Compound fault diagnosis method for gear bearing based on adaptive maximum correlated kurtosis deconvolution[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(12): 48-57. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2019.12.006 http://www.tcsae.org

