汽车碰撞速度分布分析及加速度峰值数字特征计算

唐 伟

(江苏大学 汽车与交通工程学院， 江苏 镇江 212013)

随着社会的不断发展，汽车保有量不断上升，自2000年以来，中国的汽车市场进入到发展最快速的10年[1]。但全球每年约有120万人死于碰撞产生的交通事故[2]。碰撞产生的加速度会给车内乘员造成伤害，且加速度峰值是表征汽车在碰撞时受到的最大载荷大小的一个重要参数[3]。在汽车主、被动安全系统的优化设计中，需要考虑多种随机变量，如碰撞时的车辆初速度、碰撞产生的加速度峰值等。因此，研究汽车碰撞时的速度和加速度峰值的数学特性对优化汽车设计、提高碰撞事故发生时乘员的生存率具有非常重要的意义。

国内外学者在碰撞车速分布与碰撞加速度峰值的研究中取得了丰硕的成果。Chen等[4]研究了不同车型之间的运行速度与碰撞事故发生概率之间的关系，得出以下结论：当大型车与小型车的车速差的绝对值在(10～15)km/h，同时交通流中大型车与小型车达到特定比例时，交通事故率最高。张文会等[5]建立了双向四车道、六车道、八车道事故路段仿真模型，并通过事故路段各断面平均车速绘制了车速空间分布图。Motozawa等[6]通过简化碰撞时的人、车关系，建立了简单的一维模型，在一定车速下，对理想的加速度曲线进行了推导计算，旨在寻求碰撞过程中最低的加速度峰值，从而将撞击时给人体造成的伤害降至最低。曹世理等[7]选择京津唐高速公路为研究对象，构建面板数据模型来分析车速协调性与交通安全的关系，结果表明：当同一路段各车车速间的差值小于20 km/h时可减少交通事故，提高行车安全。黄靖等[8]从具体结构形变产生的加速度入手，提出基本特征，构建加速度曲线，并通过改变加速度峰值研究其对乘员安全性的影响。李旺[9]通过对系统能量曲线的分析得到汽车B柱下端加速曲线以及关键部件的变形情况，对整车的结构耐撞性进行了分析。郑炳杰[10]通过建立汽车正面碰撞的有限元模型，从加速度变化、碰撞力变化、结构侵入量等方面对汽车结构安全性进行了初步分析和评价。

在上述研究中，对碰撞车速分布的分析主要基于高速公路中的数据。在研究加速度峰值时，都是分析某1个或某几组车速下的加速度曲线，缺少大量的碰撞事故数据支持。由于车身材料、结构变形等影响因素众多，无法确定与实际加速曲线之间的偏差，从而无法评估加速度峰值的有效性。

本文基于日常出行情况下的车辆碰撞速度进行研究分析，通过建立碰撞车速与加速度峰值的回归方程，分析随机碰撞车速下的加速度峰值以及加速度曲线。计算和分析具有数字特征的加速度峰值的期望和方差，为随机碰撞条件下汽车安全系统的优化提供统计学意义上的数据支持。

1 汽车碰撞事故时的速度分布分析

根据美国国家公路交通管理局统计的2004—2016年间汽车撞击交通事故(862起)的车速，将其按车速段统计记录，如表1所示。

从表1中可以看出:碰撞事故数先随碰撞车速增大而增多，特别是在(20～30)km/h、(30～40)km/h、(40～50)km/h这3个速度段的碰撞事故超过100起，属于汽车碰撞事故高发速度段，而速度超过150 km/h后,虽然事故严重程度增加，但是发生的次数相对较少。

表1 碰撞速度

数据来源：http://www-nass.nhtsa.dot.gov/nass/sci/SearchForm.aspx

为更直观地分析碰撞事故数的分布，根据表1画出相应的直方图，如图1所示。

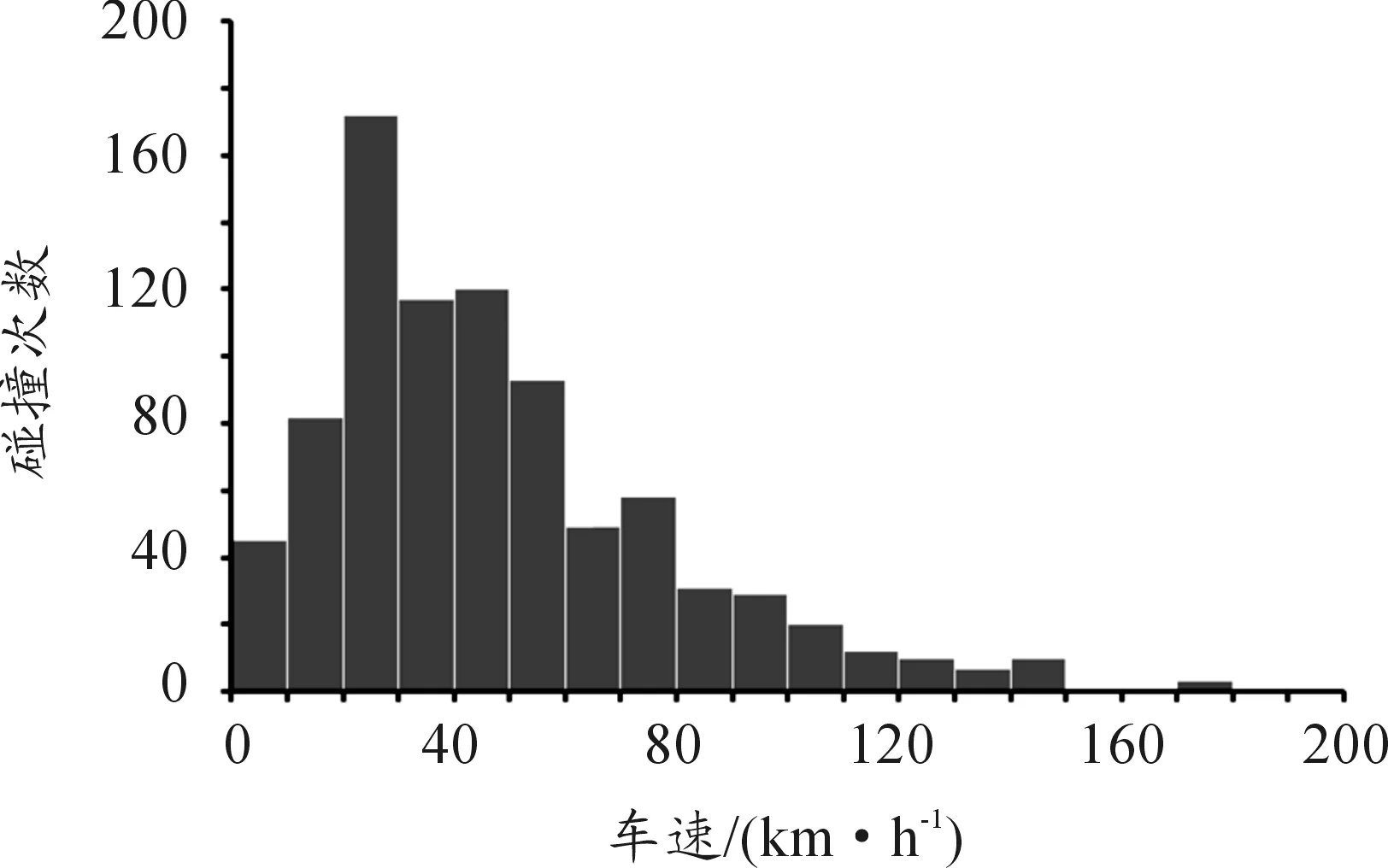
图1 不同车速区间撞车次数分布

从频率直方图中初步判定碰撞车速符合正态分布，在SPSS软件中对车速分布进行正态分布验证，结果如表2所示。

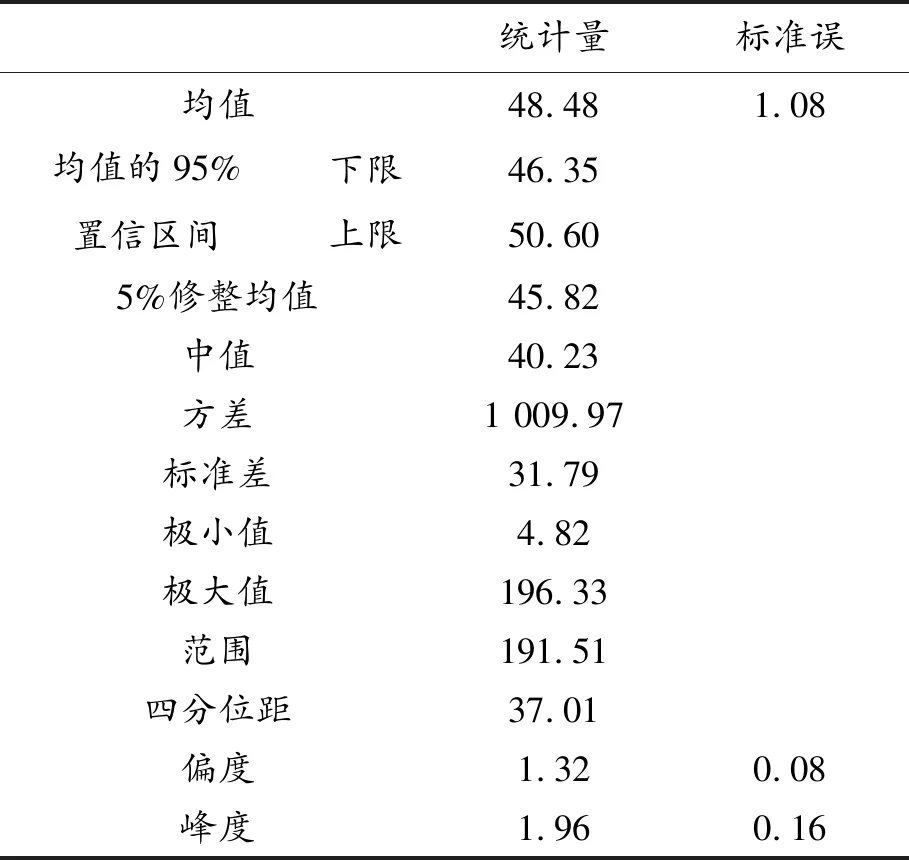
表2 正态分布验证

由于偏度为1.32，峰度为1.96，两者均小于2，可以判定撞击车速分布近似符合正态分布，可在直方图上画出正态分布曲线，如图2所示。

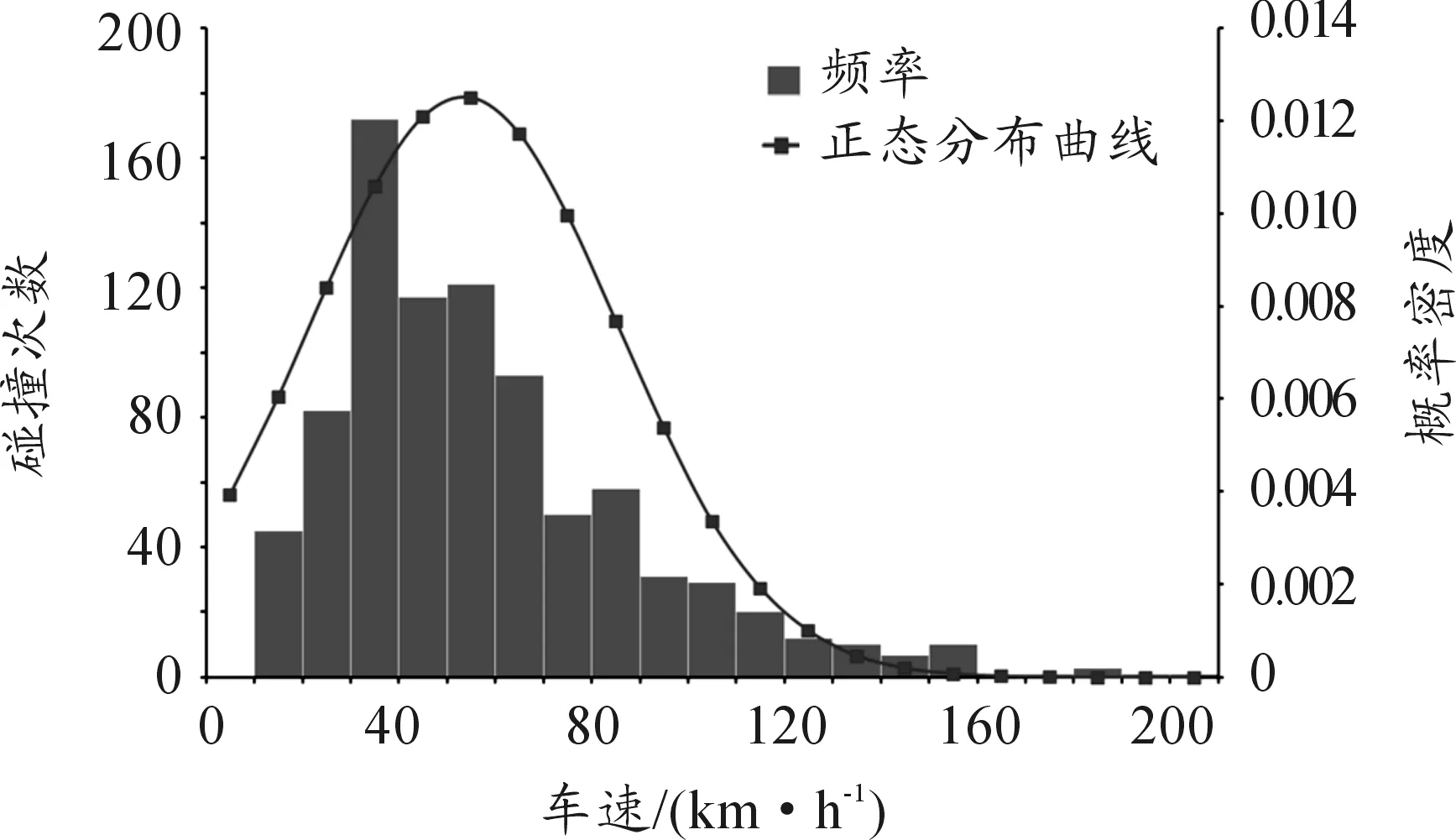
图2 车速正态分布曲线

从正态分布曲线图中看出：发生事故概率最大的车速段为(40～50)km/h。由于人们在日常出行中很少以高速行驶，碰撞概率在高速度段比较低；而以中低速度行驶的车辆数量基数大，碰撞概率反而高于高速度段。

通过表2可以得出碰撞车速的期望(均值)为48.48，标准差为31.78，从而得出碰撞车速概率密度函数，如式(1)所示。

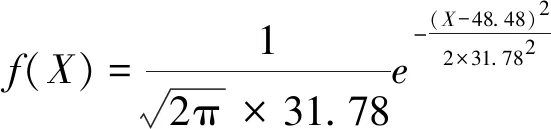
(1)

式中X为碰撞车速。

不同国家在进行汽车碰撞试验时，对用于评估汽车安全性能的车速有不同的要求。美国汽车正面碰撞安全法规中规定为48.3 km/h,日本规定为50 km/h,中国规定为50 km/h[11]，而本文通过碰撞车速分布研究，更精确地得出车速在48.48 km/h时发生碰撞的概率最大，这与各国进行汽车安全评估时的规定车速接近。由此可见，本文的研究可以为优化汽车安全设计提供更为精确、实际的数据支持。

2 建立碰撞车速与加速度峰值之间的关系

为了得出合理可靠的关系，必须在不同车速下多次试验，测量加速度峰值。为了减少试验成本和试验次数，以某试验场的DAPG-QJ-MNPZ型台车碰撞试验系统(如图3所示)为原型，建立所需的有限元仿真模型，进行不同初速度下的台车碰撞试验(图4)。

图3 台车碰撞试验系统

图4 台车碰撞系统仿真模型

2.1 有限元仿真模型的建立

台车整车用料为45钢，整车质量为400 kg，长1 800 mm，宽20 mm，高100 mm。台车上安装有撞击系统，由橄榄头和支杆构成，橄榄头直径为46.4mm，支杆直径为27.0 mm，长度为645.0 mm。支杆一边连接台车，一边连接橄榄头。撞击时，橄榄头撞击装有吸能管的导筒。吸能管采用聚氨酯复合材料，外径为59.1 mm，内孔结构设计为圆台形，靠近撞击端内径为44.5 mm，远离撞击端内径为21.8 mm。在台车撞击试验中，安装2个吸能管，吸能管安装在导筒内，导筒长655.0 mm，外径为80.0 mm，内径为59.4 mm。导筒和刚性壁障连接，刚性壁障长1 800 mm，宽20 mm，高1 000 mm。在LS-DYNA中建立模型，如图4所示。李仲兴等[12]对仿真模型可信度进行了验证，建立的仿真模型能够复现台车碰撞过程，可用于计算不同撞击车速下的加速度峰值。

2.2 撞击速度与加速度峰值回归方程

利用仿真模型进行不同初速度下的碰撞试验，并计算不同初速度下的加速度峰值，计算结果如表3所示。

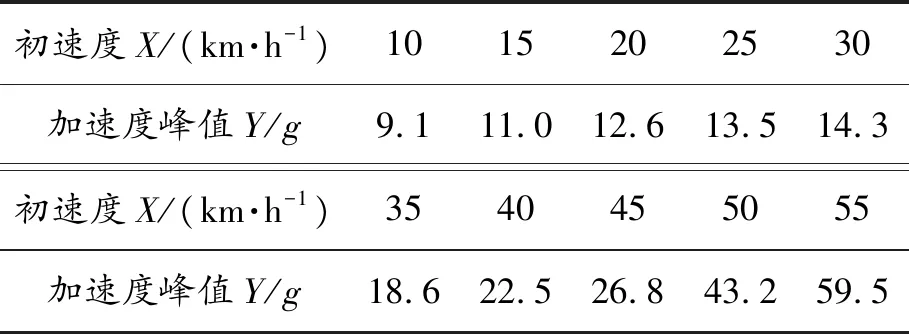
表3 不同初速度下的加速度峰值

通过表3中的数据，分别以多项式模型、指数模型、乘幂模型对碰撞车速X与加速度峰值Y的关系进行拟合。这些模型的函数形式及相关性指标如表4所示，模型的趋势线如图5所示。

表4 碰撞速度与加速度峰值回归方程

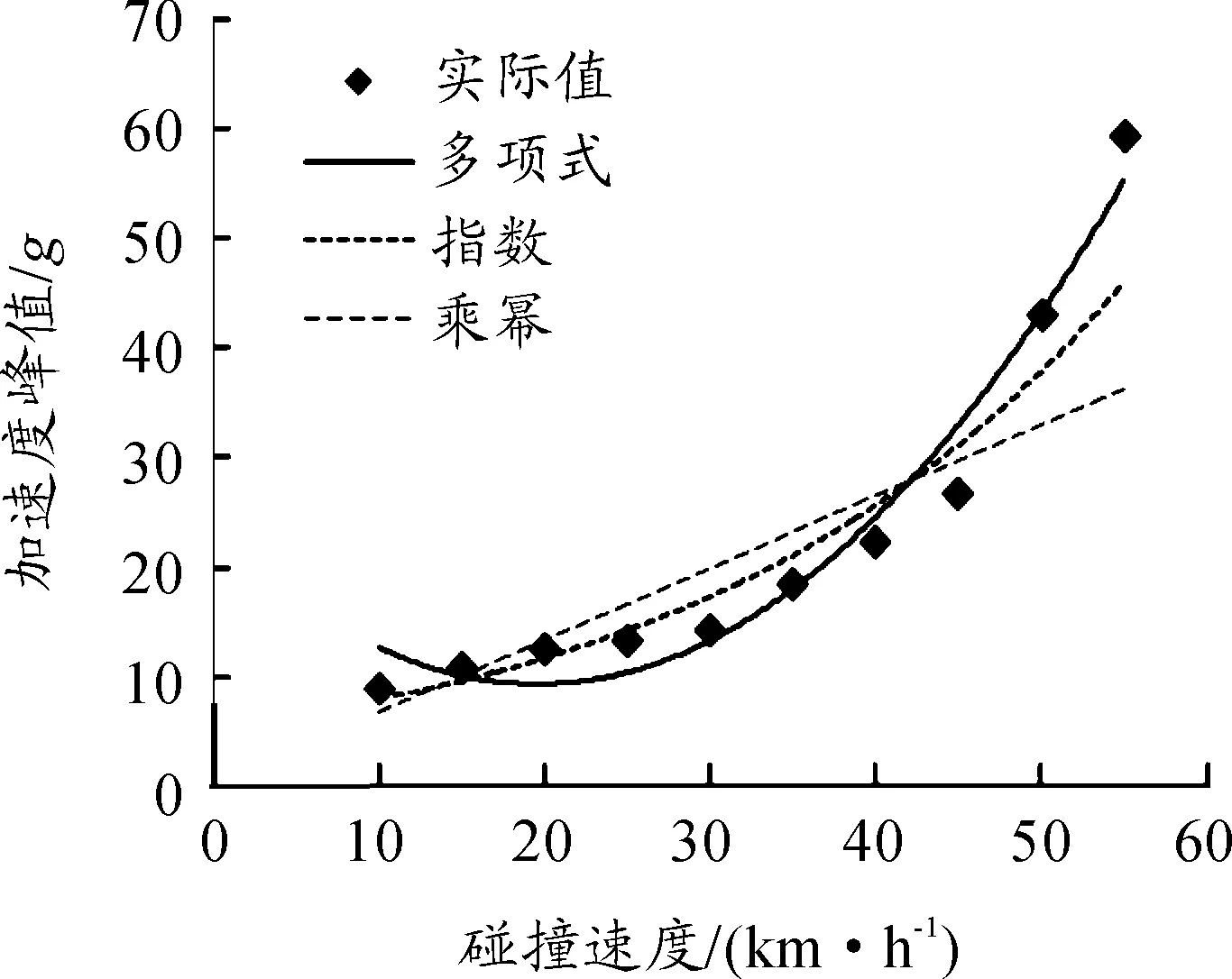
图5 撞击车速X与加速度峰值Y关系模型拟合趋势线

从上述拟合曲线可以看出，采用多项式模型的拟合效果最好(相关系数R2值最大)，因此选用多项式模型的拟合结果做进一步的分析，则撞击车速与加速度峰值的回归方程为

Y=0.036 5X2-1.426 5X+23.369

(2)

3 加速度峰值的期望和方差

利用碰撞速度概率密度函数、撞击车速与加速度峰值的回归方程以及期望和方差之间的关系对加速度峰值的期望和方差进行计算。

3.1 加速度峰值数学期望的计算

在数理统计学中，已知X的期望，Y=aX2+bX+c,则可用式(3)来计算Y的期望。

E(Y)=E(aX2+bX+c)=

aE(X2)+bE(X)+c

(3)

根据式(2)可知a=0.036 5，b=-1.426 2，c=23.36 9，则将其值代入式(3)中可得：

E(Y)=0.036 5E(X2)-1.426 2E(X)+23.369

(4)

式(4)中的E(X2)可由式(5)计算得出。

E(X2)=D(X)+[E(X)]2

(5)

式中E(X)=48.48，D(X)=1 009.97，则将其值代入式(5)中得出：

E(X2)=1 009.97+[48.48]2=3 360.3

(6)

将式(6)求得的E(X2)代入式(4)中，计算得出加速度峰值的期望为

E(Y)=0.036 5×3 360.3-1.426 2×

48.48+23.369=76.86

(7)

3.2 加速度峰值方差的计算

在数理统计学中，已知X的方差，X、Y不线性相关且Y=aX2+bX+c,则可用式(8)来计算Y的方差。

D(Y)=D(aX2+bX+c)=

a2D(X2)+b2D(X)

(8)

式中a、b、c在上面的计算中均已确定。D(X2)未知，需建立数学模型进行求解，即令Z=X2，求D(Z)。

在数理统计中，期望E(X)与方差D(X)有如下关系：

D(X)=E(X2)-[E(X)]2

(9)

则有：

D(Z)=D(X2)=E(X4)-[E(X2)]2

(10)

式中E(X2)已由式(6)计算得出，为3 360.3。E(X4)未知，可用式(11)计算。

(11)

式中f(X)为X的概率密度函数，将其代入式(11)中得：

(12)

在Matlab中运行求解式(12)得到：

E(X4)=2.2916×107

(13)

将式(6)(13)的结果代入式(10)中，得出:

D(Z)=E(X4)-[E(X2)]2=

2.291 6×107-[3 360.3]2=

1.16×107

(14)

将D(Z)=D(X2)=1.16×107，D(X)以及a、b、c的取值代入式(8)中得：

D(Y)=a2D(X2)+b2D(X)=

0.036 52×1.16×107+(-1.426 2)2×

1 009.97=1.75×104

(15)

经计算，加速度峰值的期望E(Y)=76.86，方差D(Y)=1.75×104。

汽车发生碰撞事故时，动能将在极短的时间内耗散，合理的车辆安全设计可以将车辆撞击过程中的损失降至最低。因此，利用加速度峰值期望和方差对汽车安全设计进行优化极为重要。

4 结论

1) 基于大量碰撞事故的车速进行分析，结果表明：汽车碰撞速度基本满足正态分布，汽车发生碰撞事故的概率先是随车速慢慢增大，在48.48 km/h时达到最大，之后碰撞概率慢慢减小。

2) 利用台车碰撞系统的有限元模型，计算得到多组速度下的加速度峰值，并通过回归计算得出撞击车速与加速度峰值的方程，建立碰撞车速与加速度峰值之间的关系。

3) 在得出撞击车速与加速度峰值方程的基础上，利用统计学知识，结合碰撞速度概率密度函数、碰撞车速的期望和方差，求解加速度峰值的数字特征——期望和方差，从而为随机碰撞条件下汽车安全系统的优化提供统计学意义上的数据支持。