基于历史TLE的空间目标轨道预报误差演化规律研究∗

许晓丽 熊永清

(1 中国科学院紫金山天文台 南京 210034)

(2 中国科学院空间目标与碎片观测重点实验室 南京 210034)

(3 中国科学院大学 北京 100049)

1 引言

自从1957年第1颗人造卫星被送入太空以来,人类就拉开了航天活动的序幕,卫星运动的轨道成为人们关注的焦点之一,轨道精度的话题也随之展开.随着人类航天活动的蓬勃发展,在轨空间目标(人造卫星、空间碎片等)的数量不断增加,对大量空间目标进行监视和轨道确定成为保障航天任务顺利完成的重要一环.由于空间目标的轨道真值目前只能用估计的轨道代替,而在这个过程中测量误差、模型误差等各种因素会导致轨道确定和预报不可避免地存在误差.

如何获得空间目标的轨道误差信息是空间目标监视和空间目标轨道数据应用中不可或缺的一项工作.实际工作中常用内符合和外符合两种形式来定义轨道确定精度[1],目前对轨道预报误差进行分析确定的方法主要有以下3类[2]: 基于轨道模型的误差外推、与高精度星历对比和基于历史轨道数据的误差分析.

基于轨道模型的误差外推方法可以得到精度较高的误差协方差矩阵,该方法需要已知高精度轨道模型和初始协方差.一般情况下采用精密定轨的方法产生初始协方差,但解算的参数往往会在一定程度上包含部分测量误差和力学模型误差,导致这种误差外推方法得到的误差值往往偏小,得到的误差协方差矩阵对应的轨道精度偏高,与事后验证的实际轨道精度不符,所以在目前的研究中较少采用.

轨道预报误差也可以通过轨道预报星历和高精度星历对比进行评估,但需要精度更高的轨道数据作为参考.Chan等[3]对比了地球静止轨道通信卫星群的TLE(Two Line Element)预报轨道结果和双站测距轨道确定系统的轨道预报结果,分析了轨道预报误差随时间和空间的变化规律,指出TLE数据的轨道误差在时间序列上表现出一致性,没有明显变化,而对于不同地理区域表现出明显的系统偏差,并且偏差的大小和方向与经度方向的重力加速度相关.Muldoon等[4]通过对比TLE预报星历和GPS卫星精密星历结果,指出TLE数据中不仅包含着坐标系旋转偏差,而且存在着模型误差.Xu等[5]将CHAMP(Challenging Minisatellite Payload)卫星的历史TLE轨道和GPS精密星历比对,分析和讨论了TLE编目轨道的误差特征和分布,指出CHAMP卫星的TLE轨道误差随地理经度变化明显,沿迹方向出现+1000 m到−1400 m的系统偏差,均方差稳定在500 m左右.然而对于空间目标编目中的大多数目标无法得到其高精度轨道确定结果,所以只能针对少量有精密星历的卫星进行轨道精度评估.

对于大多数空间目标,利用历史轨道数据进行误差统计分析是较为可行的方法.该方法通过比较历元时刻的轨道状态和先前轨道数据预报到该时刻状态得到残差信息.这种方法的前提是空间目标的编目管理是稳定的,即目标的系列轨道根数的精度水平大致相当.实际上,基于历史数据的误差分析,给出的是轨道数据序列的一致性.Aerospace公司很早就通过对地球同步卫星的历史轨道数据统计分析给出了地球同步轨道卫星的平均轨道预报误差演化模型[6].Kelso[7]分析了TLE数据的一致性,并指出TLE数据的一致性分析可以很好地近似TLE的精度分析.Osweiler[8]利用历史数据计算了TLE轨道预报误差协方差矩阵,并给出了协方差的自相关函数.Wang等[9]按照轨道高度、偏心率对近地目标进行分类,并基于历史TLE统计和分析了近地目标中各分类轨道的误差演化特征.陈磊等[10]考虑了轨道预报误差的周期特性,采用泊松级数对TLE的轨道预报误差进行拟合,更全面地描述了轨道预报误差随预报时间的长期变化和随在轨位置的周期变化.

美国空间监视网(Space Surveillance Net,SSN)是目前世界上最先进的空间监视系统,对在轨目标进行编目和维护.NORAD(North American Aerospace Defense Command)将大部分空间目标的轨道信息以双行根数的形式在Space-Track网站上定期公布.TLE是用特定方法平滑掉了周期扰动项的平均轨道根数,对应的SGP4/SDP4(Simplified General Perturbation Version 4/Simplified Deep-space Perturbation Version 4)模型是解析模型.TLE数据由于其完备性、实时性、精确性及开放性而备受关注,被广泛应用于空间态势分析和空间目标碰撞预警等方面.然而TLE数据并没有包含轨道精度信息,使其应用受到限制.

许晓丽等[11]通过仿真模拟的方法研究了TLE编目体系的轨道误差特性,结果表明轨道误差与观测弧段的约束密切相关,观测资料的变化会干扰编目轨道误差的周期变化特性.不同目标的轨道周期变化的稳定性不一样,因而我们着眼于TLE轨道预报误差的中长期演化特征进行研究.

本文在前人基础之上,实现了基于历史TLE数据的轨道预报误差自动生成与建模技术.其主要流程为: 根据输入的目标编号和统计时间窗口,自动下载Space-Track网站上发布的历史TLE数据,利用定轨标预报的方法生成轨道误差数据,并对误差数据进行野值预处理,通过区间划分的方法进行统计分析,得到误差数据的均值和标准差序列,最后采用二次多项式进行拟合,输出目标集合的轨道预报误差演化模型数据,并以来自不同类型轨道—LEO(Low Earth Orbit)、MEO(Medium Earth Orbit)、HEO(High Earth Orbit)和GEO(Geosynchronous Earth Orbit)—的5个典型目标作为代表,对其轨道预报误差演化规律进行了研究和分析.最后对4种类型轨道的所有目标的误差演化特征进行了统计,给出了7 d内轨道预报误差随时间变化的均值和均方差,并拟合给出了其对应的平均解析模型.

2 方法

2.1 轨道预报误差数据的生成

由于空间目标的真实轨道是未知的,只能用估计的轨道来近似.一般而言,定轨精度总是高于预报精度,当预报期达到一定程度后,定轨精度将比预报精度高得多,可以作为基准来标定轨道的预报精度.因此,利用某历元时刻的轨道预报状态量XPRG减去此时的轨道估计状态量XEST便可生成预报误差,即:

TLE轨道预报误差数据生成的具体流程和方法为: 对指定历史时间段内按照时间先后顺序排列的NTLE组编目数据,采用SGP4/SDP4模型将统计时间窗口内的所有历元TLE根数逐一外推至预报时间门限T内所有的标准历元时刻(即定轨根数历元时刻),然后进行逐一比对,图1为流程示意图.

图1 TLE轨道预报误差数据生成流程示意图Fig.1 The flow diagram of TLE orbital prediction error generation

从Space-Trcak网站上选择了2018年6月18日给出的最近30 d有数据更新的空间目标集合(LEO、MEO、HEO和GEO目标共计3953个),并下载了1 yr(从2017年1月1日至2017年12月31日)的历史根数,预报时间门限为7 d.为了更好地分析轨道预报误差的演化特征,将TLE数据从真赤道平春分点坐标系(TEME)转换到地心惯性坐标系(J2000),并将轨道预报误差数据分解到U、N、W方向,其中U轴与轨道相切并指向速度方向,N轴位于轨道平面内垂直于速度方向,W轴垂直于轨道平面,构成右手直角坐标系.

2.2 轨道预报误差数据的统计方法

2.2.1 误差数据的区间划分

由于观测条件及测站分布等原因,TLE根数的历元分布并非完全等间隔,这给预报位置误差随时间变化的统计拟合带来一定的困难.然而大多数TLE根数生成的历元时刻在轨道升交点附近,误差数据的历元时间差的分布与目标轨道周期呈现出明显的倍数关系.根据这一特性,可以依据轨道周期对误差数据进行区间划分,从而分组进行统计.然而,LEO、MEO、HEO和GEO 4种轨道类型目标的数据更新频率、轨道周期各有特点,因此在保证一定统计数据量的基础上,我们根据4种轨道类型目标1 d内运动的圈数进行具体划分.

若目标的轨道周期为t(d),预报历元时间差为∆t,由于历元时间差并非轨道周期的整数倍,取与其最近的非零整数N∆t/t作为其近似值,则N∆t/t的最小值为1,最大值为int(T/t).对于LEO目标,为了保证数据量满足统计需求,采取3个轨道周期为一个统计区间进行划分,划分的区间数NLEO可表示为:

对于MEO、HEO和GEO目标,采取1个轨道周期为统计区间进行划分,划分的区间数可表示为:

2.2.2 误差数据中的野值问题

由于观测粗差及轨道异常等原因,TLE数据中不可避免地存在野值,相应的轨道预报误差中也会存在野值.通常采用均值和标准偏差来统计描述轨道预报误差的演化结果,而均值和标准偏差容易受极端值的影响,因此需要对误差数据中的野值进行剔除.采用基于马氏距离的异常值检测方法[12–14],对于每一个数据组,计算所有数据点到数据分布中心的马氏距离dM,若dM超过预设的门限值,则将该数据点视为异常值进行剔除.

2.2.3 误差数据的统计和拟合

针对‘干净’的误差时间序列,重新计算每一个区间内误差的平均值和标准差.以每个区间的平均值为中心、标准差为误差棒,可以描述预报误差随预报时间的演化规律.最后,采用二次多项式进行最小二乘拟合,可以得到每个目标轨道预报误差在U、N、W方向上的演化解析模型,并给出拟合的相关系数.在拟合过程中可能会出现的几种情况:(1)误差数据分布符合空间目标轨道预报演化的一般规律,二次多项式拟合相关系数较高;(2)误差数据分布不太符合空间目标轨道预报演化的一般规律,二次多项式拟合相关系数较低;(3)误差系数极大,严重超出了预报精度的一般水平,这需要对该目标的轨道数据进一步分析和挖掘,考虑是否存在变轨等轨道异常情况;(4)误差数据较稀少和离散,无法进行统计和拟合.

2.3 轨道预报误差系数生成与建模

输入目标编号集合和统计时间窗口命令,采用脚本语言对以上流程实现自动化处理,包括TLE根数下载、TLE根数预报比对、轨道误差数据生成、误差数据的统计拟合等.命令执行后自动生成每一个目标的误差演化解析模型: 包括目标编号、TLE组数、各方向(U、N、W)误差均值系数和均方差系数及拟合相关系数.

3 轨道预报误差演化规律分析

空间目标轨道预报误差由初始误差和模型误差两部分组成.在进行轨道预报时,初始误差会随着轨道模型的外推而传播,传播特性和趋势因轨道类型的不同而不同.通过定轨目标预报方法确定的轨道预报误差实际上描述的是动力学模型误差的传播.影响空间目标运动的摄动因素很多,其中地球非球形引力、大气阻力、第3体引力及太阳光压等摄动是最主要的因素,它的取舍与目标的轨道高度及偏心率相关.为了描述各类空间目标的轨道运动特征,我们选取了5个目标作为代表(LEO目标由于大气摄动的影响随高度变化显著,选取了不同轨道高度的两个目标,MEO、HEO和GEO目标各选取1个目标)对其轨道预报误差演化规律进行分析.所选的5个目标及其主要轨道参数在表1中列出,其中最后1列给出了目标在所选时间段内的历史根数数量.

表1 所选空间目标的轨道参数Table 1 Orbital parameters for the selected space objects

采用上述误差生成与统计方法,画图分别分析5个代表性目标的轨道预报误差演化规律,如图2–6,其中,“ ”代表目标的误差分布,“◦”给出每个误差区间的平均值,以平均值为中心的误差棒代表每个误差区间的标准差.总体上来说,轨道误差随预报时间发散,U方向误差(沿迹方向)占主导,N方向和W方向误差相对较小.图2给出了轨道高度为387 km的LEO目标在U、N、W3个方向的误差预报随时间的演化结果,由于大气阻力对轨道的摄动影响显著,沿迹方向轨道误差快速发散,预报7 d接近300 km,N方向的轨道预报误差7 d接近5 km,W方向的误差预报7 d在2 km左右.图3给出了轨道高度在700 km左右的近圆目标在U、N、W3个方向的误差预报随时间的演化结果,由于大气密度随高度变化接近指数函数,大气对轨道的影响减弱,3个方向的误差预报7 d均不超过1 km,其中N方向误差最小,预报7 d在0.2 km左右.从图中还可以明显看出,N、W方向的预报误差表现出明显的系统性偏差,并随预报时间线性增大.对于轨道高度在20000 km左右的地球半同步轨道卫星,预报7 d,U方向误差不超过2 km,N和W方向误差均不超过0.5 km,如图4所示.对于大椭圆轨道目标,由于受到的摄动因素比较复杂(在近地点时大气阻力摄动较大,在远地点时日月引力和光压摄动较大),U方向误差发散较严重,预报7 d甚至可达30 km,并表现出轻微的系统偏差,如图5所示.对于选取的地球同步轨道卫星,其轨道高度约为35800 km,由于受到的日月摄动较大,误差明显较发散,预报7 d轨道误差达到10 km左右,如图6所示.

图2 目标41763轨道预报误差在U、N、W 方向上随时间的变化Fig.2 Orbit prediction error variation of the object 41763 in U, N,and W directions

采用最小方差二次多项式分别对5个典型目标轨道预报误差的标准差进行拟合,给出其近似的轨道预报误差演化解析模型:σ=A0+A1∆t+A2∆t2.其中∆t为预报时间,单位为d,σ为轨道预报误差标准差,单位为km,A0、A1和A2分别为二次项拟合系数的常数项、线性项和二次项.5个目标U、N、W方向预报误差标准差的拟合系数如表2所示,其中最后1列给出了拟合结果的相关系数.

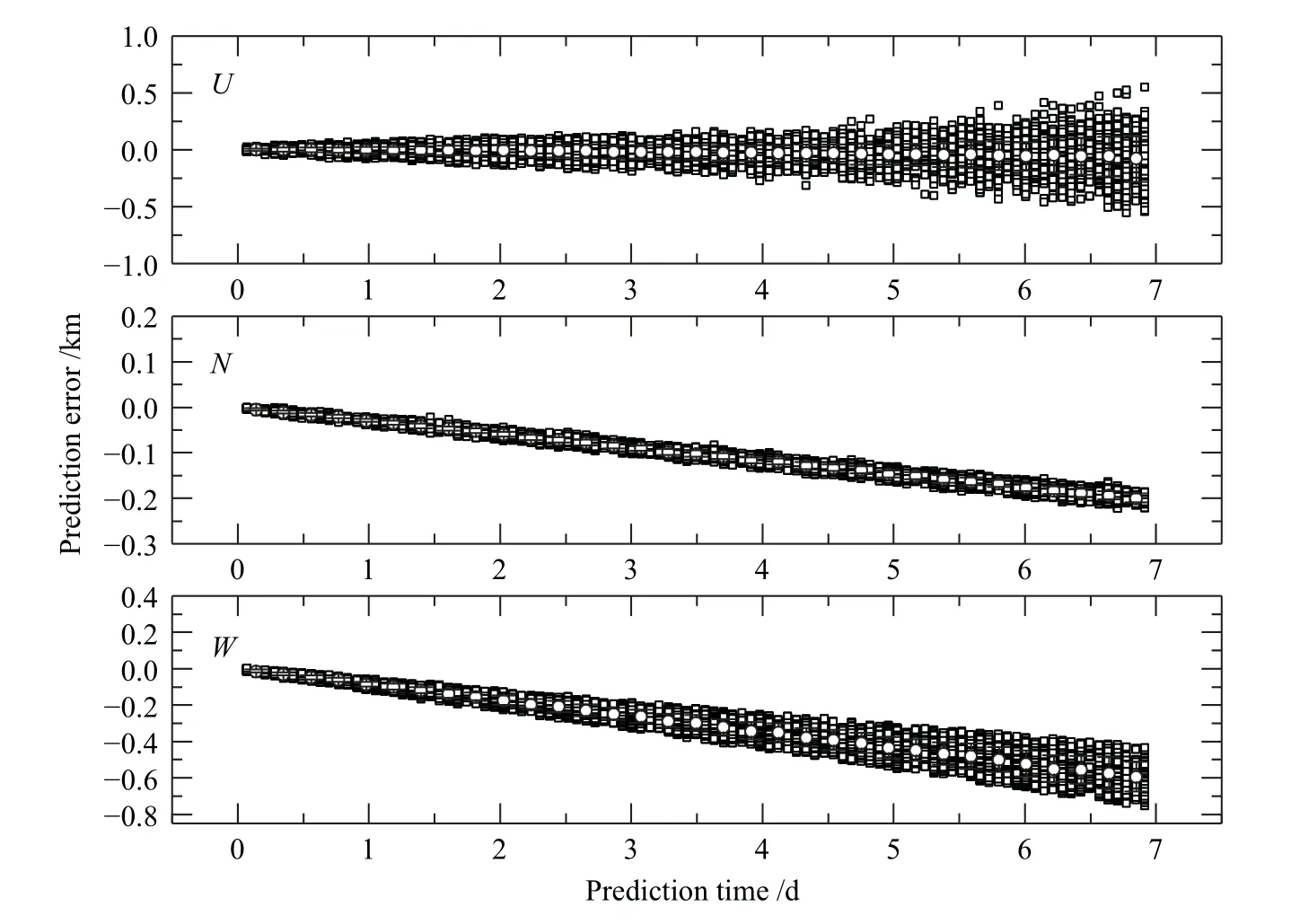
图3 目标22675轨道预报误差在U、N、W 方向上随时间的变化Fig.3 Orbit prediction error variation of the object 22675 in U, N,and W directions

图4 目标23204轨道预报误差在U、N、W 方向上随时间的变化Fig.4 Orbit prediction error variation of the object 23204 in U, N,and W directions

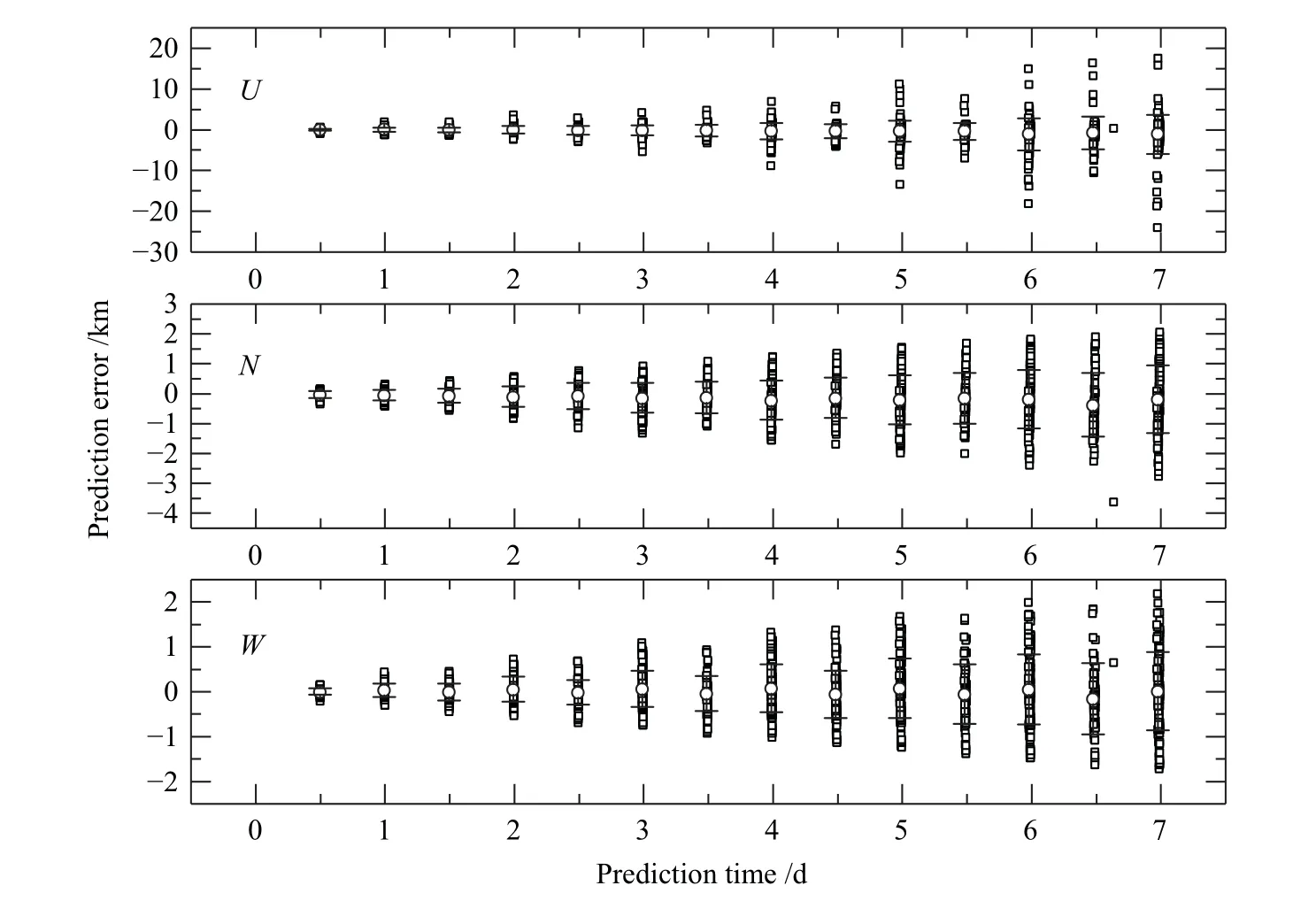
图5 目标08015轨道预报误差在U、N、W 方向上随时间的变化Fig.5 Orbit prediction error variation of the object 08015 in U, N,and W directions

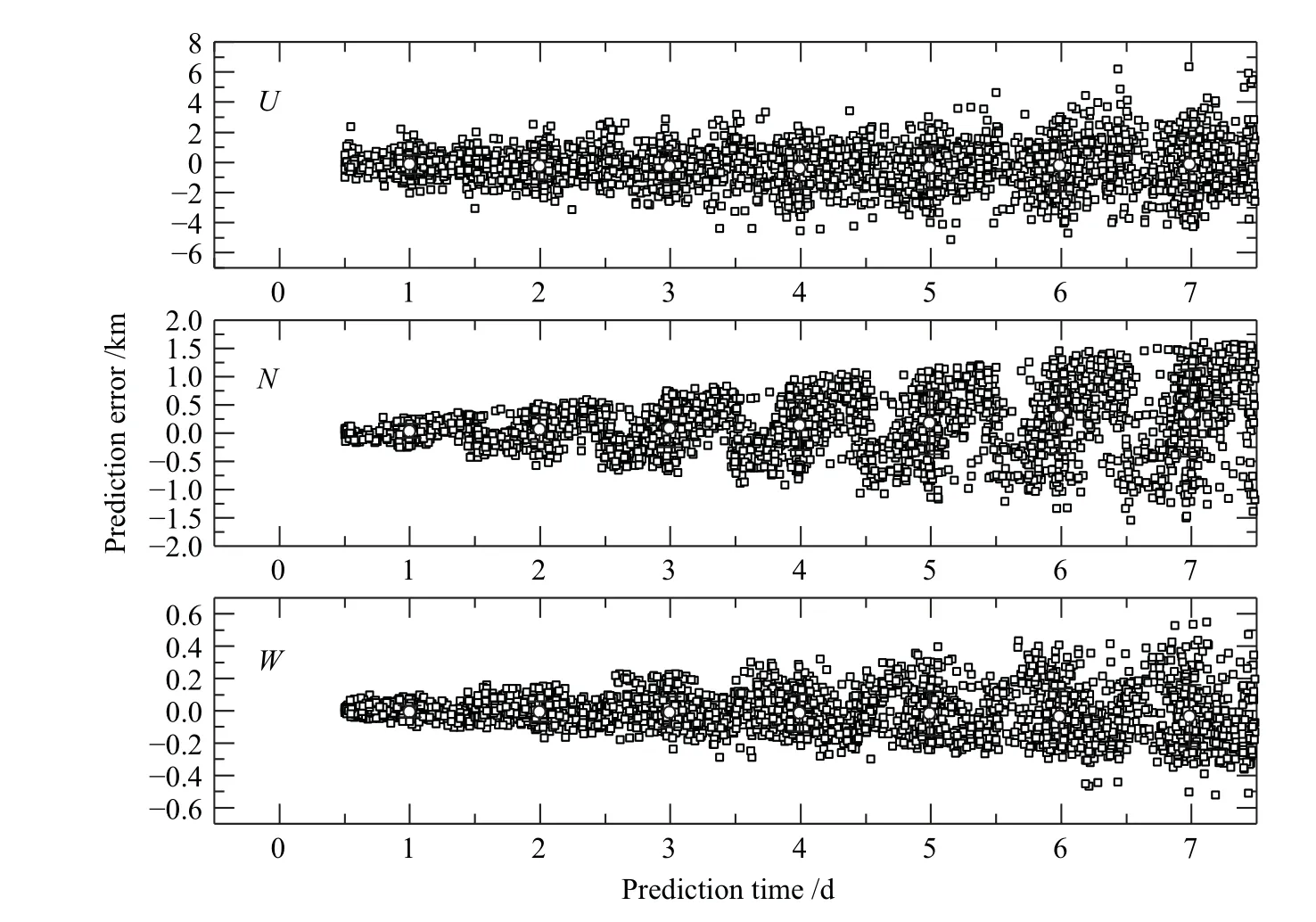
图6 目标25050轨道预报误差在U、N、W 方向上随时间的变化Fig.6 Orbit prediction error variation of the object 25050 in U, N,and W directions

表2 5个典型目标U、N、W方向轨道预报误差标准差的二次项拟合系数Table 2 Quadratic fitting coefficients of the standard deviations of orbit prediction errors for the five typical targets in U, N,and W directions

4 4种轨道类型空间目标轨道误差演化规律统计

尽管Kelso[7]指出每一个目标的轨道误差预报具有特殊性,需要单独分析,不能用同类型轨道来完全代表,但是分类统计能够在一定程度上反映同类轨道目标的轨道预报误差整体演化的趋势和量级大小.另外,并不是所有空间目标都能够获得足够的历史轨道数据来进行预报误差统计分析与建模,在这种情况下用同类轨道目标的轨道预报误差来代替是一种较可行的方法.因此,我们针对所选的空间目标集合的所有轨道误差进行分类统计分析.

根据Space-Trcak网站上给出的空间目标轨道分类标准,即0.25、MEO : 600 minTP800 min且e <0.25、HEO :e >0.25、GEO : 0.99将所研究的3953个目标按照轨道特征分成4类.其中,目标平均运动角速度、为地球平均自转角速度、e为轨道偏心率、TP为目标运动轨道周期.所有目标集合中,LEO目标2692个、MEO目标221个、HEO目标190个、GEO目标850个.根据误差数据的统计拟合情况,我们选取其中拟合系数相关系数较高(>0.9)的误差系数,分别对每一类目标的误差演化进行统计分析.4类目标的统计采样数分别为1964、205、135、753,统计结果分别如表3–6,给出了U、N、W方向轨道预报误差均值(Avg)和标准偏差(SD)的平均值随时间演化的统计结果,同时还给出了均值和偏差的最大值及最小值,以更全面反映4类目标轨道预报误差随时间演化的范围.从表中可以看出,U方向误差占主导,N方向和W方向误差相对较小.LEO目标由于受大气阻力影响较严重,沿迹方向轨道预报误差很快发散,预报7 d接近10 km; MEO目标的轨道预报误差最小,沿迹方向预报7 d仅1 km左右; HEO目标由于大偏心率受到大气阻力和第3体引力摄动的影响,沿迹方向预报误差发散较快,预报7 d超过10 km; GEO目标轨道误差在沿迹方向预报7 d接近20 km.另外,从统计的平均值来看,整体上来说4类目标轨道误差的系统性偏差很小,但有些目标会出现较大的系统性偏差,尤其是在沿迹方向上.

表3 1964个LEO目标轨道预报误差演化统计结果Table 3 Statistical results of orbital prediction error variation for 1964 LEO objects

针对表3–6中的统计数据,采用最小二次曲线拟合,分别给出LEO、MEO、HEO和GEO 4种轨道类型空间目标轨道预报误差随时间演化的平均解析模型,表7列出了各系数结果.我们可以看出,LEO目标和HEO目标沿迹方向轨道预报误差随时间平方快速增长,N和W方向误差几乎呈线性增长.GEO目标沿迹方向误差线性项系数较大,增长很快.

表4 205个MEO目标轨道预报误差演化统计结果Table 4 Statistical results of orbital prediction error variation for 205 MEO objects

表5 135个HEO目标轨道预报误差演化统计结果Table 5 Statistical results of orbital prediction error variation for 135 HEO objects

表6 753个GEO目标轨道预报误差演化统计结果Table 6 Statistical results of orbital prediction error variation for 753 GEO objects

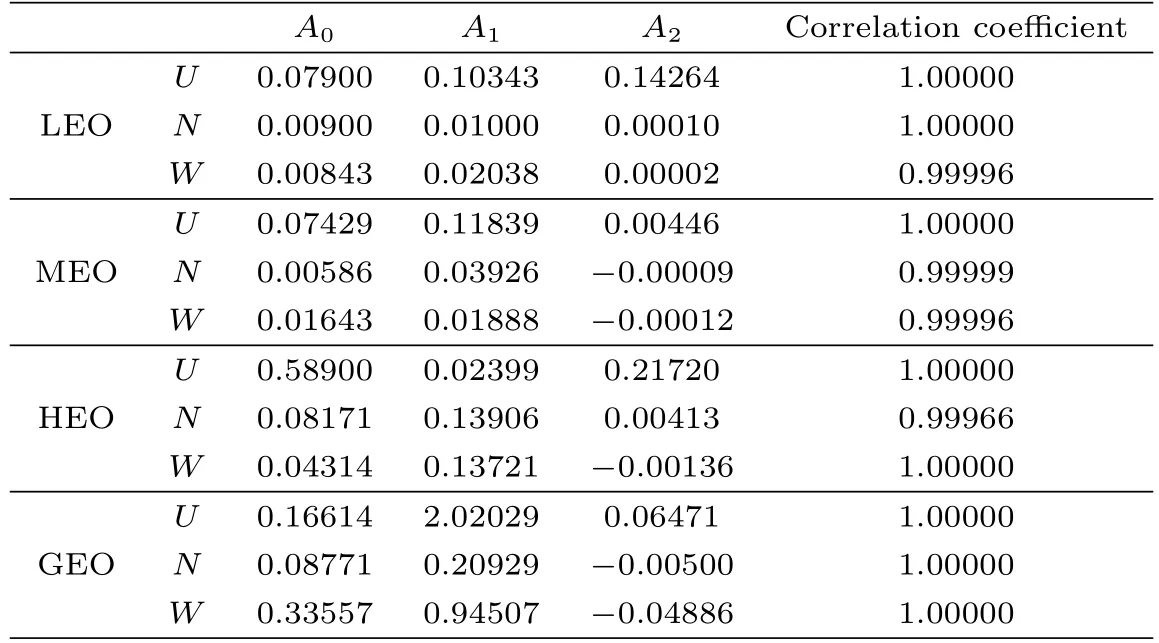
表7 4类典型空间目标轨道预报误差随时间演化的平均解析模型系数Table 7 Average analytic model coefficients of the orbit prediction errors evolving with time for the four kinds of typical space objects

5 结论

本文基于历史TLE数据实现了空间目标轨道预报误差自动生成与建模技术.基于3953个目标1 yr的历史TLE根数和SGP4/SDP4模型进行轨道预报,利用定轨标预报的方法生成轨道误差数据,通过区间划分和统计拟合生成了空间目标轨道预报误差演化系数.分类讨论了4种轨道类型目标轨道预报误差随时间的演化规律,分别给出了LEO、MEO、HEO和GEO目标轨道预报误差在U、N、W方向随时间演化的平均解析模型.根据平均解析模型,可以快速了解不同类型空间目标轨道预报误差演化的趋势和量级,给TLE数据在空间目标编目管理及碰撞预警等实际工作中的应用提供一些参考.