Tunable coupling between Xmon qubit and coplanar waveguide resonator∗
He-Kang Li(李贺康), Ke-Min Li(李科敏), Hang Dong(董航), Qiu-Jiang Guo(郭秋江), Wu-Xin Liu(刘武新),Zhan Wang(王战), Hao-Hua Wang(王浩华),†, and Dong-Ning Zheng(郑东宁),4,‡
1Institute of Physics,Chinese Academy of Sciences(CAS),Beijing 100190,China
2Zhejiang Province Key Laboratory of Quantum Technology and Device,Department of Physics,Zhejiang University,Hangzhou 310027,China
3School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China
4CAS Center for Excellence in Topological Quantum Computation,University of Chinese Academy of Sciences,Beijing 100049,China
Keywords: superconducting Xmon qubit,qubit-resonator coupling,tunable coupling
1. Introduction
Practical quantum computing requires a large-scale quantum network, which may build upon millions of qubits.[1,2]For this particular reason superconducting qubits,whose high scalability is guaranteed with modern microfabrication technologies, have become a promising platform and have recently attracted significant research attention.[3]A lot of work has been done to improve the qubit design and quality in a planar architecture.[4-8]The energy lifetime, which is one of the most important performance metrics for the qubit, is improved to 10 µs-50 µs for two-dimensional (2D) transmon qubits.[9,10]Various types of superconducting quantum processors, on which multiple transmon qubits are integrated with either only neighbor couplings for a 2D grid[11,12]or allto-all couplings through a common bus resonator,[13,14]have been fabricated and successfully used for the quantum error correction,entanglement generation,and quantum simulation experiments.[12-14]
However, most of qubit-qubit and qubit-resonator coupling schemes used in these quantum processors are capacitive through non-tunable capacitors; therefore, couplings can hardly be turned off unless the qubits are detuned far away in frequency, which is difficult to implement due to limited frequency tunability. Since residue couplings may cause unwanted operation errors when qubits are supposed to be isolated in the gate control sequences,a tunable coupling scheme with a high ON/OFF coupling ratio that is also easy to operate is highly desired. In 2014, Chen et al.[15]reported a tunable coupler between two inductance-shunted Xmon qubits, also called Gmons. Since then, more theoretical investigations on tunable couplers have appeared.[16,17]Recently,Neill et al.[18]reported a blueprint for demonstrating quantum supremacy with a chain of Gmon qubits featuring neighboring tunable couplings, where they randomly turned on and off the couplings between randomly chosen Gmon qubits to allow quantum excitations to shuttle among the qubit chains. Since the couplers are the only elements being actively controlled during the experimental sequences, the coupler performance really determines whether or not the quantum supremacy experiment with Gmon qubits will succeed.
In this article, we show a variant of the Gmon coupling scheme that can be adapted to an all-to-all connected circuit architecture,an inductive coupler used between an Xmon qubit and a coplanar waveguide resonator. By changing the flux in the Josephson-junction loop of the coupler, the qubitresonator coupling can be turned on and off at will. The coupling strength is experimentally verified to be adjustable from 0 MHz to about 40 MHz,and the energy relaxation time of the Xmon qubit can still be up to 12µs with the coupler in use.
2. Design and fabrication
As shown in Fig. 1(a), to enable the inductive coupling element, the traditional Xmon qubit is shunted with an additional line inductance,Lg. The inductance line(orange color)goes across the bus resonator via an airbridge and, together with the resonator’s center trace,divides the ground into four quadrants. The first and third quadrant host a gradiometer loop with a Josephson junction at the input as the tunable coupler,which is almost insensitive to the external perturbing flux noise.
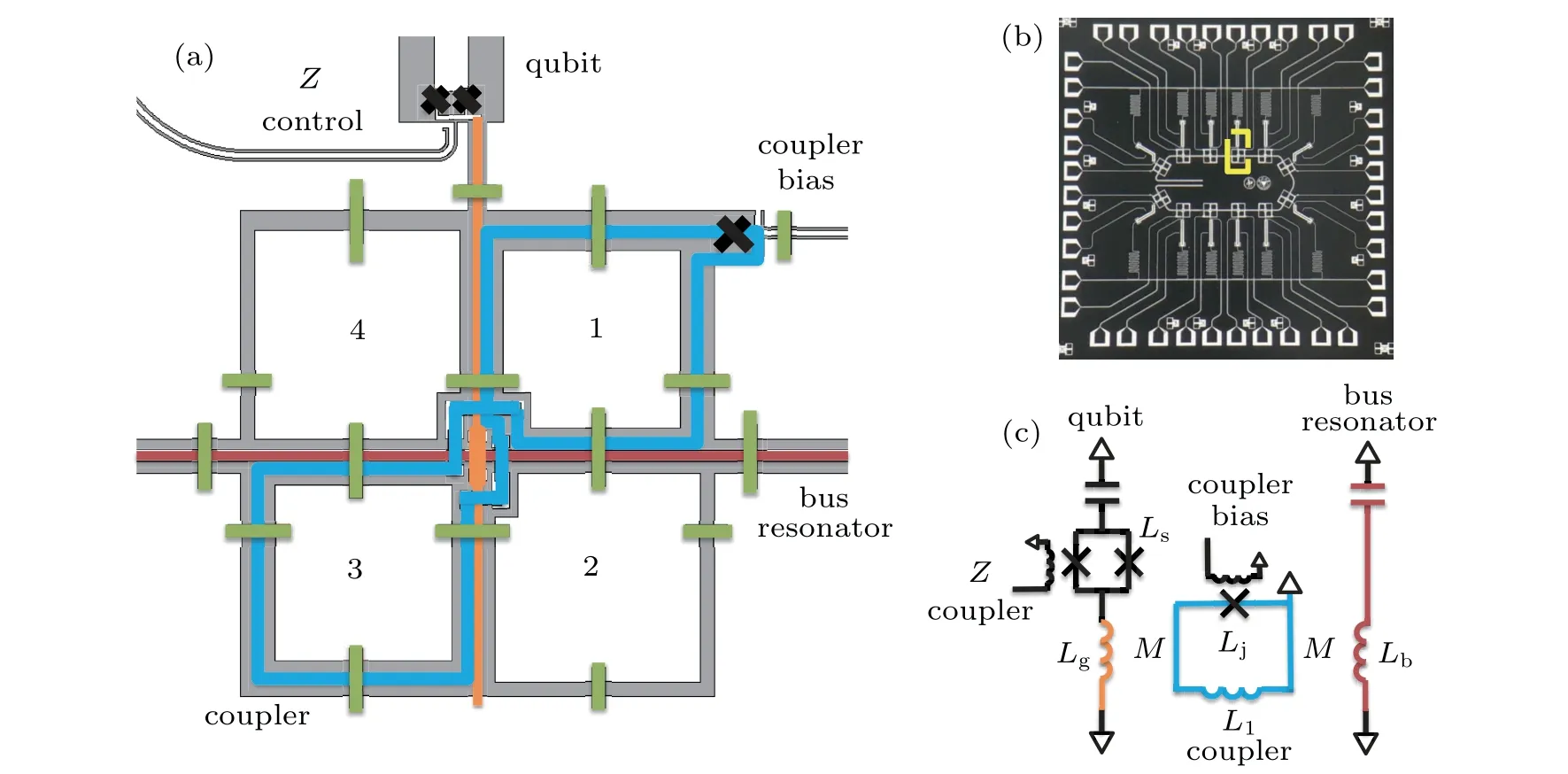
Fig.1. (a)Layout schematic diagram of tunable coupler. (b)Optical micrograph of entire circuit chip featuring multiple Xmon qubits coupled to central bus resonator. Schematic in panel(a)refers to area enclosed in yellow square. (c)Equivalent circuit schematic plot showing Xmon qubit,bus resonator,and tunable coupler in between. Cross symbol refers to Josephson junction.
The Xmon qubit consists of a line-shaped capacitor resonating with a nonlinear inductor Ls= 8.1 nH from a dc SQUID. To minimize the interference of the shunting inductance,we use a linear inductor Lg=0.31 nH so that Lg≪Ls.When current I flows through the qubit, the magnetic flux Φ that can be sensed by the bus resonator via the coupler is
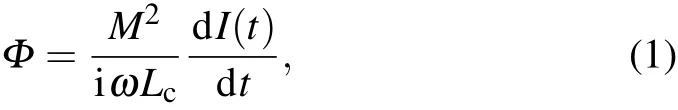
where ω is the frequency of the oscillating current, M =0.085 nH is the qubit-coupler mutual inductance, and it is also the coupler-resonator mutual inductance, and Lc=Ll+Lj/cosφjis the total inductance of the coupler. Here Ll=0.81 nH is the geometric loop inductance, Lj= 0.9 nH is the Josephson junction inductance, and φjis the phase difference across the junction. With the screening parameter β =Ll/Lj<1 for this rf-SQUID, no hysteresis in flux will affect the tuning.
The effective mutual inductance M′between the Xmon qubit and the bus resonator can be calculated from

Therefore, the effective coupling strength g between the qubit and bus resonator is
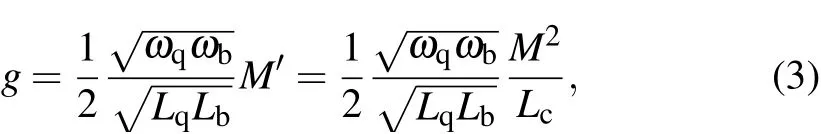
where Lq=Lg+Ls/cosφsis the qubit inductance, φsis the phase difference across the SQUID, Lb=1.13 nH is the inductance of the bus resonator,and ωq(ωb)is the resonant frequency of the qubit (bus resonator). When φj=π/2 for the Josephson junction in the coupler,Lcapproaches to infinity so that the effective coupling strength,g,approaches to zero.
A device was fabricated with this design, as shown in Fig.1(b).First,100-nm-thick aluminum film was deposited on a sapphire substrate by electron beam evaporation with a base pressure better than 10-9Torr (1 Torr=1.33322×102Pa).Second, a standard wet-etch process was used to define the overall wirings of the circuit: Photoresist(SPR955) was spin coated and then the structures,other than the Josephson junctions or airbridges, were defined on the coated photoresist by photolithography, following which the etchant was used to transfer the lithography pattern onto the aluminum film.Third,two types of Josephson junctions-one is for the qubits and the other one for the couplers - were fabricated using the Dolan-bridge technique[19]with different exposure doses:500 nm of MAA and 300 nm of PMMA that were spin coated on the top of the aluminum wirings sequentially, with AR-P 5090 as the conducting layer on the top. Subsequently, the Josephson junctions were patterned by E-beam lithography.Following which, the Ar ion cleaning and the double angle evaporation of two layers of aluminum films with an oxidation process sandwiched in between were carried out in E-beam evaporator.Finally,airbridges were fabricated in a similar way to that described in Ref.[20]. The device was then measured in the dilution refrigerator.
3. Results and discussion
As shown in Fig. 2, we first benchmark the qubit coherence performance with an existing coupler. A typical energy relaxation time in several qubits is about 12 µs, and a typical phase relaxation is about 4µs near the optimal bias point(which is not shown here). These results are comparable to those reported in Ref. [15]. Therefore, we conclude that the coupler,though imposing complications in the device fabrication,interferes negligibly with the qubit lifetime.
Figure 3(a)demonstrates the functionality of the tunable coupler,where the coupling strength data(dots)are compared with the numerical calculations(line). The experimental data are processed from the measured swap dynamics between the qubit and bus resonator by using the pulse sequence shown in Fig. 3(b). With the coupler bias fixed, we first drive a πpulse to excite the qubit at 5.63 GHz to its |1〉 state, following which we apply a square pulse with a variable amplitude of z-pulse amplitude (ZPA) to the qubit flux line, so that the qubit is tuned to a frequency around the bus resonator for energy swap dynamics with a variable delay time. The resulting qubit|1〉-state probability P1is measured right after the interaction,which is plotted as delay time versus ZPA in Fig.3(c).The well-defined Chevron patterns indicate the energy swap process, and the period along the delay axis in the center of a Chevron pattern correlates with the coupling strength. It is seen that the coupling strength between the qubit and bus resonator varies with the coupler bias,which is in agreement with Eq.(3).The coupling strength increases quickly as the coupler bias is tuned close to half the flux quanta,and the experimentally measured coupling strength can be up to-42.7 MHz.We note that the negative sign here is due to the fact that φjof the coupler junction takes a value near π for Lc=Ll+Lj/cosφjin Eq.(3),while Fourier transform of the P1data in Fig.3(c)only gives the amplitude of the coupling strength. The experimentally characterized range of the coupling strength is from 0 to about 40 MHz.

Fig.3. (a)Measured coupling strength,g/2π versus coupler bias(dots)in comparison with the numerical calculation(line). (b)Experimental pulse sequence used for the qubit-resonator swap dynamics,where qubit is excited to|1〉at 5.63 GHz and then biased with ZPA to a fixed frequency around the resonator for energy exchange process. (c)Qubit|1〉state probability,P1(color bar on the far right)and delay time versus qubit’s ZPA,measured with the experimental pulse sequence shown in panel(b)at three coupler biases as numbered in panel(a). The coupling strength is estimated from Fourier transform of the data in panel(c)(For clarity in display the y scales are different for the color plots).
4. Conclusions and perspectives
We have designed and fabricated a tunable coupler between an Xmon qubit and a coplanar waveguide resonator.With the qubit-resonator swap dynamics, we experimentally show that the coupling strength can be adjusted from 0 MHz to about 40 MHz,and the qubit energy relaxation time can still be up to 12µs. This tunable coupler design can be easily adapted to an all-to-all connected circuit architecture where multiple qubits couple to a common bus resonator, and therefore will become an active building block to minimize the crosstalk error for scalable quantum electronics.
Acknowledgment
The authors thank Fengliang Dong, Peipei Chen form the National Center for Nanoscience and Technology and Haifang Yang, Aizi Jin, Guangzhou Geng, and Shi Yan from Laboratory of Microfabrication, Institute of Physics, Chinese Academy of Sciences for help in the micro-fabrication of samples.
- Chinese Physics B的其它文章
- Exploring alkylthiol additives in PBDB-T:ITIC blended active layers for solar cell applications∗
- Study on the nitridation of β-Ga2O3 films∗
- Thin-film growth behavior of non-planar vanadium oxidephthalocyanine∗
- Monolithic semi-polar(1¯101)InGaN/GaN near white light-emitting diodes on micro-striped Si(100)substrate∗
- Spectral properties of Pr:CNGG crystals grown by micro-pulling-down method∗
- Quaternary antiferromagnetic Ba2BiFeS5 with isolated FeS4 tetrahedra

